饱和粉质黏土动弹性模量影响因素分析及骨干曲线模型研究

庄妍，朱伟，张飞



饱和粉质黏土动弹性模量影响因素分析及骨干曲线模型研究

庄妍1, 2，朱伟1, 2，张飞1, 2

(1. 河海大学 岩土力学与堤坝工程教育部重点实验室，江苏 南京，210098；2. 河海大学 岩土工程科学研究所，江苏 南京，210098)

为了研究交通动荷载作用下地基土动弹模量的变化规律，利用室内动三轴试验系统对东南沿海地区饱和粉质黏土进行动三轴试验，研究围压、超固结比、孔隙比和应变幅值对动弹性模量变化规律的影响；采用经典Hardin−Drmevich等效线性模型，提出考虑超固结比、孔隙比影响的饱和粉质黏土动弹性模量修正公式。研究结果表明：在相同应变水平下，动弹性模量随着围压和超固结比增大而增大，随着孔隙比增大而减小；与经典Hardin−Drmevich公式相比，本文提出的动弹性模量修正公式对试验结果的拟合效果更好。

饱和粉质黏土；动弹性模量；动三轴试验；修正Hardin−Drmevich模型

我国沿海及沿江地区广泛分布着大量深厚软土层。软土是指在靠海地区、河流三角洲地区、湖泊河塘地区、洪积沼泽等水流缓慢的区域，土体沉积并经过复杂的生化反应形成的饱和软黏性土。软土具有天然含水率高、孔隙比大、压缩性高、抗剪强度低、渗透性差、灵敏度高及流变性显著等特点[1]。近年来，我国沿海地区经济迅猛发展，大量基础工程如温州机场工程[2]、京沪高速铁路工程[3]、杭甬高速公路工程[4]，上海地铁1号线工程[5]等投入建设，但这些工程均建设在软土地层上。交通工具在运行过程中由于振动作用会形成循环荷载，与静荷载相比具有长期性和反复性。在长期循环荷载作用下，地基土体的结构会发生改变，使得地基稳定性降低，工后沉降量增加，从而降低工程的使用年限。动弹模量是影响软土沉降的关键因素，对于动荷载作用下软土弹性模量变化规律的研究具有十分重要意义。HARDIN等[6]认为，动模量阻尼比的影响因素有13~15个；汪明元等[7]利用GDS(global digital systems)轴向加载系统，以浙江省舟山市岱山深海(水深大于20 m)海底原状海相软土为研究对象，开展应变控制下的动三轴试验，发现随着围压增大，软土动弹性模量显著提高。徐毅青等[8]通过对上海地铁隧道周围加固软黏土进行GDS试验，系统探讨循环荷载振动频率、循环动应力幅值、初始偏应力及围压对动弹性模量的影响。刘飞禹等[9]等通过室内动三轴试验，研究了循环荷载作用下初始偏移应力、荷载频率、超固结比以及循环应力比等对软土动弹性模量衰减的影响。邱成春等[10]以不同围压下的加筋饱和砂土(以有机玻璃作为加筋材料)为研究对象，开展了一系列循环荷载下的动三轴试验，研究了加筋饱和砂动弹性模量及阻尼比随围压、动应变、竖筋高度的变化规律，从而得到最大动弹性模量与围压的关系。郑刚等[11]研究了振动频率对饱和黏土动力特性的影响，认为振动频率对软黏土的动弹性模量影响不可忽略，在不同振动频率下动弹性模量随轴向应变增加而减小。李又云等[12]对黄土的动力特性进行研究，发现固结应力比、周围压力、干密度、动应力、含水量对土的动弹性模量均有影响。廖红建等[13]对饱和重塑黄土进行了一系列等向固结和偏压同结下的排水与不排水动三轴试验，发现偏压固结和固结围压增大使骨干曲线上移，土体强度增大。DARENDELI[14]指出影响黏土弹性模量的主要因素有应变幅值、围压及孔隙比。李校兵等[15]采用变围压动三轴系统研究了循环围压对饱和软黏土动模量的衰减规律。刘家顺[16]采用动三轴仪对粉质黏土进行不同条件下的动力特性试验，研究了固结围压、含水率、振动次数、静偏应力等对动剪切强度及动弹模量的影响，发现固结围压及含水率是影响粉质黏土动强度的主要因素。但以上研究均未同时考虑围压、孔隙比、超固结比和应变幅值对动弹性模量的影响，为此，本文作者以东南沿海地区饱和粉质黏土为试验土样，通过DDS−70三轴试验系统，综合考虑围压、超固结比、孔隙比和应变幅值对饱和粉质黏土动弹性模量变化规律的影响；提出Hardin−Drmevich动弹性模量修正公式，以期为实际工程中软土的动力特性分析提供参考。

1 试验设计

1.1 试验土样特性及制作

试验用土取自南京地区，取土深度约为−4 m，土呈灰色，不含杂质。根据JTG E40—2007“公路土工试验规程”[17]，将土样晒干，然后，过孔径为0.5 mm的筛，取粒径小于0.5 mm的土样作为试验用土。经室内试验测得土的基本物理性质如表1所示。试验时按照试验仪器要求制作试样：试样直径为39.1 mm，高为80 mm。

1.2 试验方案

本次试验采用DDS−70微机控制电磁式振动三轴试验系统对南京地区粉质黏土进行动力性能测试。该测试系统可以用来测量土的动弹性模量、动强度和阻尼系数等土动力指标。通过改变不同试验条件，分别研究围压、超固结比、孔隙比、动应变对粉质黏土动弹性模量的影响。本次试验共设计10组试验，具体试验方案如表2所示。

表1 土的基本物理性质

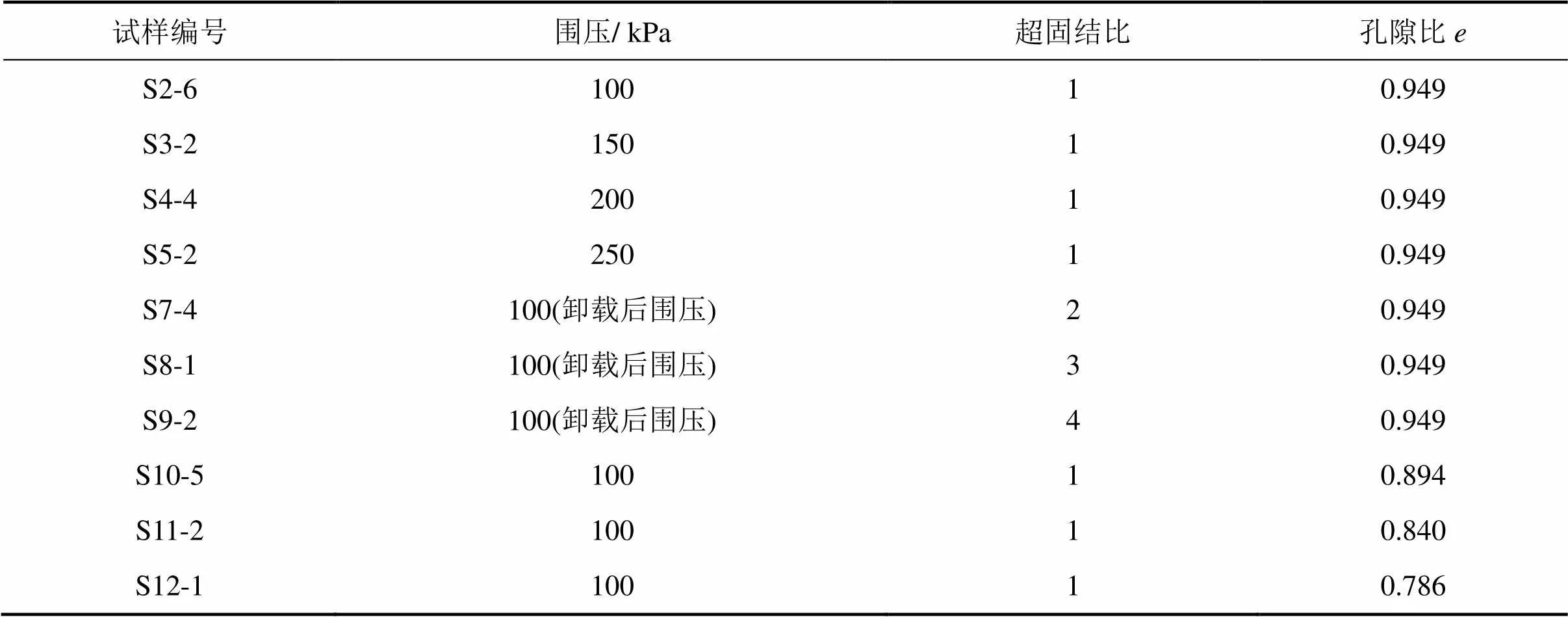
表2 动三轴试验方案

2 试验结果

2.1 围压对土体动弹性模量的影响

图1所示为不同围压下土体的动弹性模量d与动应变d的关系。由图1可知：当其他条件相同时，不同围压下d−d曲线形式相同，d随着d的增大呈非线性减小；对于相同的动应变d，围压越大，动弹性模量d越大，这是因为围压越大，试样土颗粒之间的接触更加充分，土体结构变得紧实，试样强度增加。从图1还可以看出：围压对d的影响随着d增大而减小。根据动弹性模量减小的程度，可将d随d增大的变化情况划分成以下3个阶段。

1)当d＜0.2%时，动弹性模量d随着动应变d的增大而急剧减小，试样的强度急剧降低；当d=0.2%时，动弹性模量与最大动弹性模量的比值小于50%。

2) 当0.2%＜d＜1.0%时，动弹性模量d随着动应变d的增大而缓慢减小，强度变化不大。

3) 当d＞1.0%时，动弹性模量d几乎不随动应变d的增大而变化，围压对动弹性模量d几乎没有 影响。

2.2 超固结比对土体动弹性模量的影响

图2所示为不同超固结比下土体的动弹性模量d与动应变d的关系。由图2可知：当动应变d相同时，超固结比越大，动弹性模量越大；当动弹性模量d相同时，超固结比越大，动应变d越大，并且动弹性模量d随着动应变d的增大而呈非线性减小。

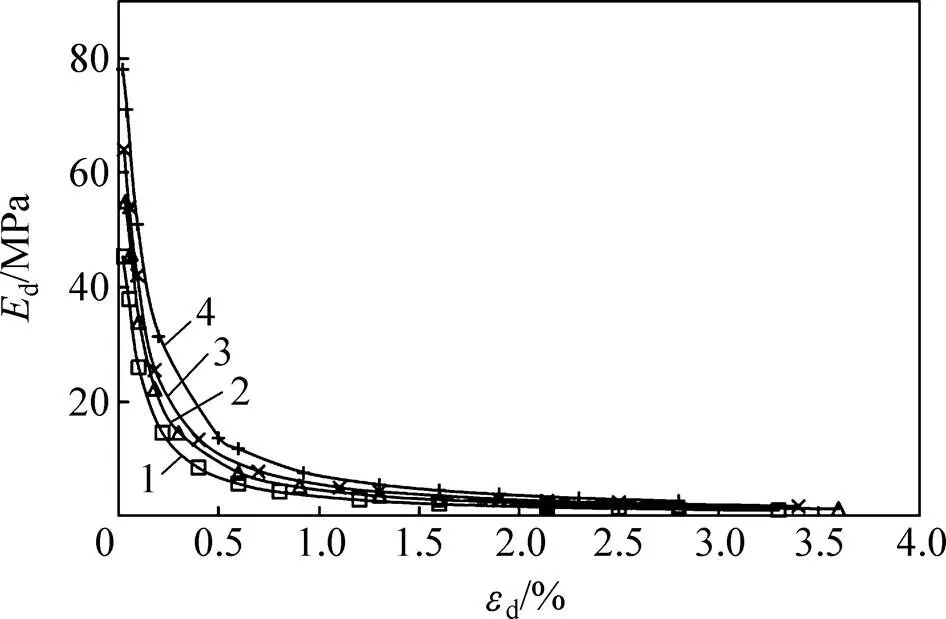
围压/kPa：1—100；2—150；3—200；4—250。

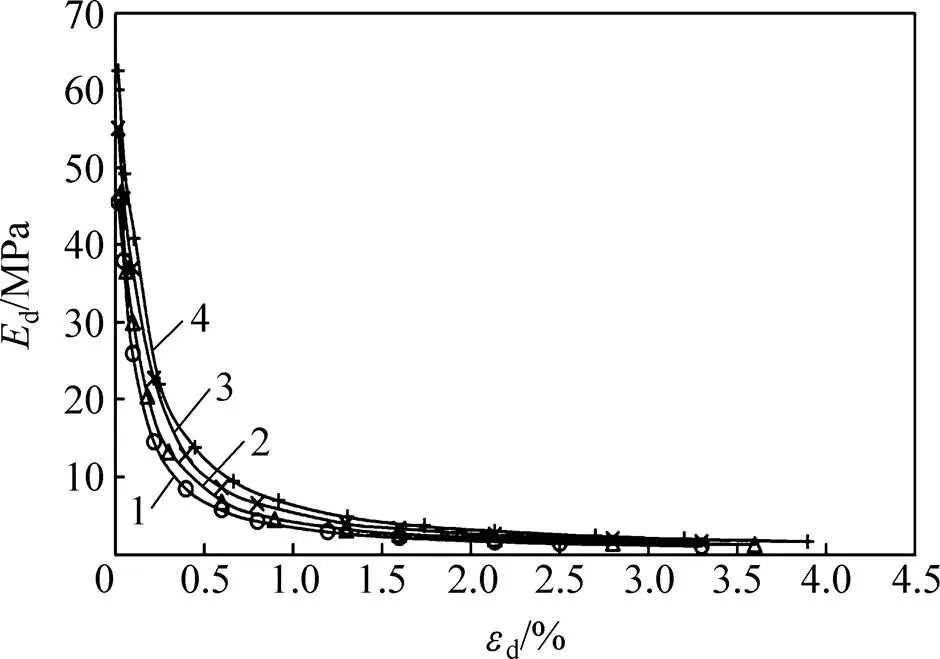
超固结比：1—1；2—2；3—3；4—4。

2.3 孔隙比对土体动弹性模量的影响

图3所示为不同孔隙比下d与d的关系。由图3可知：不同孔隙比条件下得到的动弹性模量d与d关系曲线趋于重合，由此可见孔隙比对动弹性模量d的影响较小。

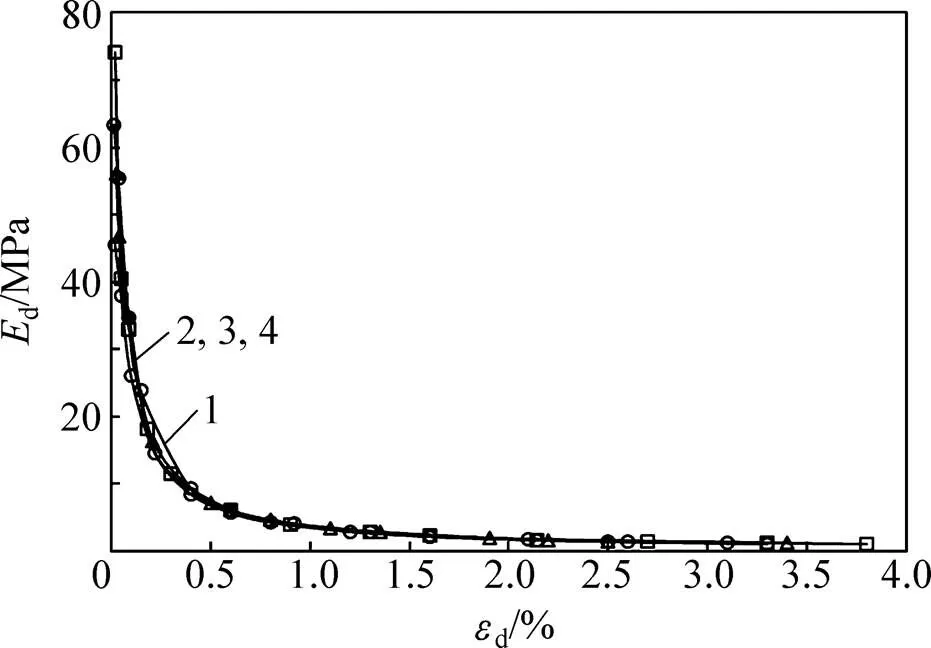
孔隙比：1—0.949；2—0.894；3—0.840；4—0.786。

3 骨干曲线模型的建立

动弹性模量试验的研究范围是小应变[18]，其表达式[19]为

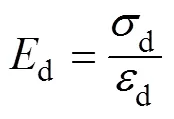
式中：d为动应力。

HARDIN等[20]针对土的非线性动力特性，提出了Hardin-Drmevich等效线性模型。该模型把土视为黏弹性介质，描述了动轴向应力d与动轴向应变d之间的关系，并定义曲线的割线斜率为动弹性模量d。模型可表达为

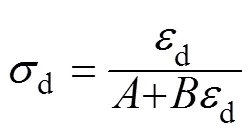
将式(2)代入式(1)可得

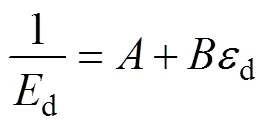
分别令动轴向应变d=0和d=∞，则有

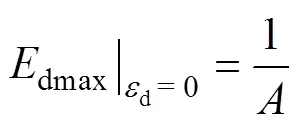
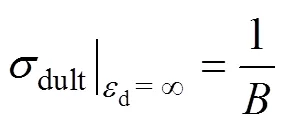
定义相对线应变幅值dr的表达式如下：

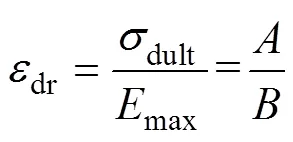
式中：dmax为最大弹性模量；dult为当→∞时动轴向应力的最大值。

将式(4)~(6)代入式(2)可得

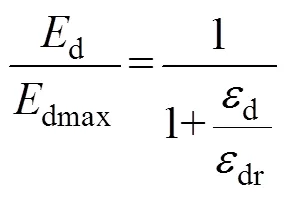
由式(3)可知：动弹性模量的倒数1/d与动应变d呈线性关系，根据试验结果可得到不同条件下动弹性模量的倒数1/d与动应变d的关系。

图4所示为不同围压下的1/d与d的关系。由图4可知：1/d与d呈良好的线性关系，可用直线拟合；围压越大，拟合的直线斜率越小；在动应变相同的情况下，1/d随着围压增大而减小。

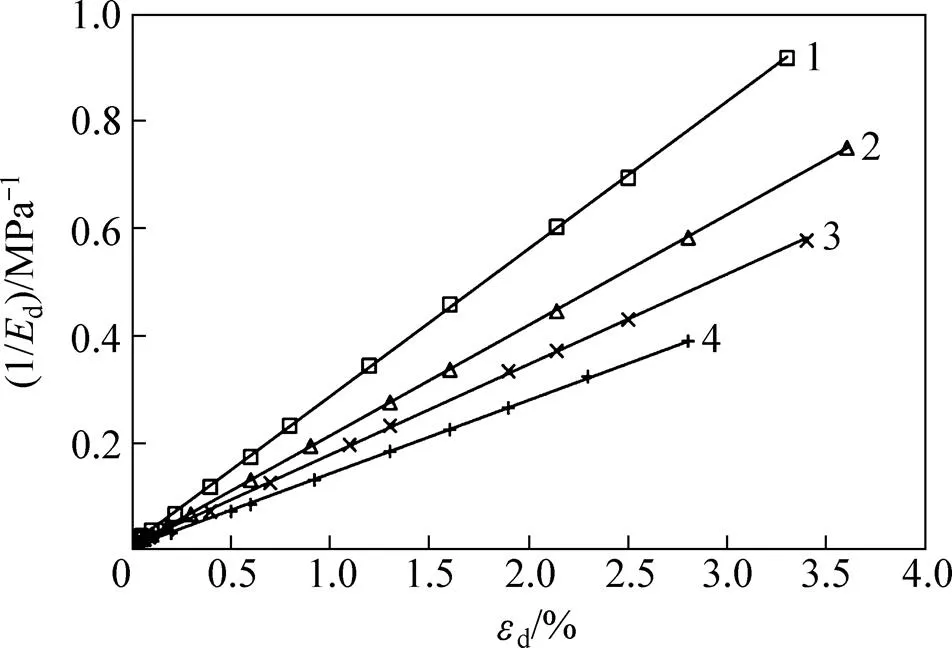
围压/kPa：1—100；2—150；3—200；4—250。

图5所示为不同超固结比下1/d与d的关系。由图5可知：1/d与d基本呈线性关系，可用直线拟合；超固结比越大，拟合的直线斜率越小；在动应变相同的情况下，1/d随着超固结比增大而减小。

图6所示为不同孔隙比下1/d与d的关系。从图6可以看出：1/d与d基本呈线性关系，可用直线进行拟合；在动应变相同的情况下，1/d随着孔隙比增大而增大，但增大幅度较小；不同孔隙比对应的1/d−d曲线几乎重合。

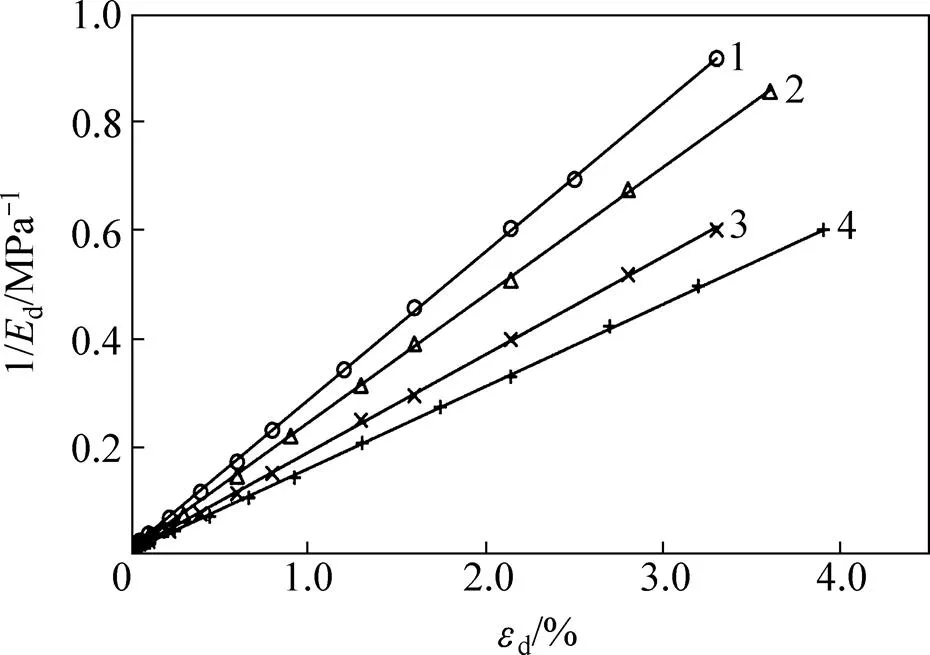
超固结比：1—1；2—2；3—3；4—4。

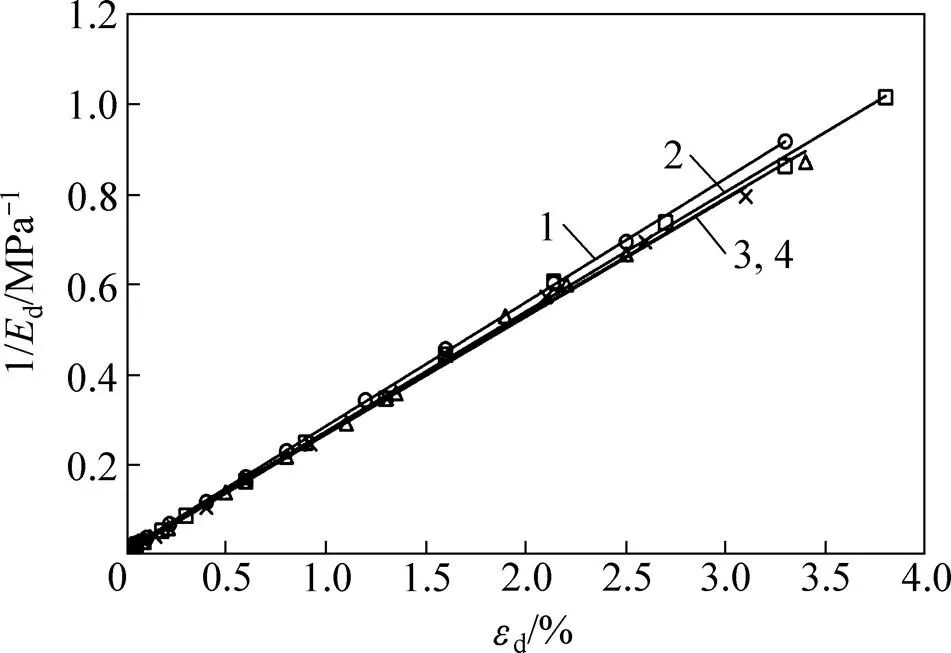
孔隙比：1—0.949；2—0.894；3—0.840；4—0.786。

由式(4)可知：图4~6中直线的截距为1/dmax，截距的倒数为dmax。对试验结果进行回归分析可得如下拟合公式：

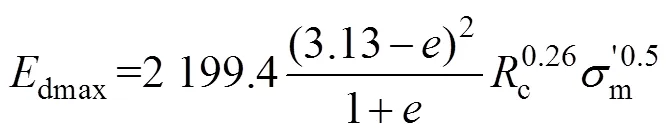
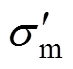
为了提高试验数据的拟合度，对式(8)进行修正：

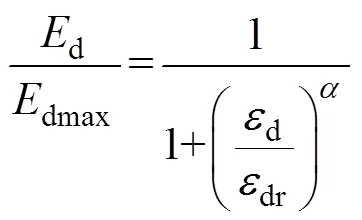
经过归一化分析可知=1.15。

对不同试验条件下dr进行回归分析：

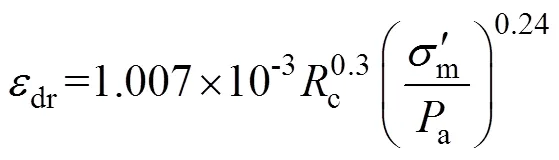
式中：a为大气压力。

将式(8)和(10)代入式(9)得到动弹性模量修正公式：

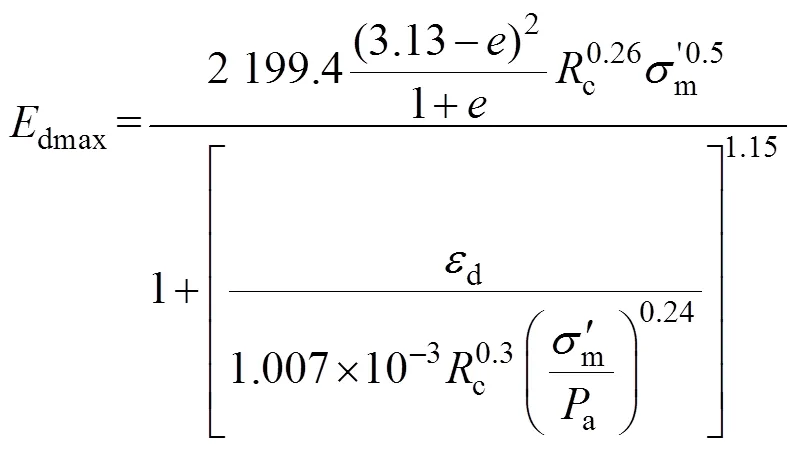
4 修正动弹性模量公式有限元模型验证

4.1 模型尺寸及材料参数

建立桩承式路堤三维有限元数值分析模型，模型中沿行车方向的长度为6.0 m，垂直行车方向宽度为5.2 m，模型整体垂直方向高度为25.8 m，其中面层厚度为0.8 m，路堤填土厚度为2.8 m，桩顶上方垫层厚度0.2 m，地基土部分厚度为22.0 m，桩长为11.0 m，桩径0.5 m，桩间距1.5 m，有限元模型示意图如图7所示。模型中面层、基层、底基层、桩体及加筋体采用线弹性材料模拟，路堤填土及地基土层部分采用摩尔−库仑材料模拟，各部分采用的材料参数如表3所示。在模型顶部施加循环移动荷载，荷载循环数为 100次。

4.2 修正动弹性模量公式验证

模型中黏土层分别考虑弹性模量变化与不变化2种情况。路基黏土层表面、两桩距离中心点处土的累积沉降随循环荷载加载次数的变化如图8所示。从图8可以看出：不论弹性模量是否变化，路基表面中心处黏土前期累积沉降量随循环荷载加载次数增大而增大且增速较快，后期累积沉降增幅较小直到趋于稳定；当弹性模量变化时，累积沉降在循环荷载加载15次后增长缓慢，循环荷载加载100次时模型中土的沉降量计算值为122.67 mm；当弹性模量不变时，累积沉降量在循环荷载加载10次后增长缓慢，在循环荷载加载100次时模型中沉降量计算值为108.43 mm。根据现场实测结果，桩间土沉降量实测值为 120.00 mm，考虑变化情况下循环荷载加载100次时桩间土沉降量计算值为122.67 mm，计算值与实测值相对误差为2.2%；考虑恒定情况下循环荷载加载100次时桩间土沉降量计算值为108.43 mm，计算值与实测值相对误差为9.6%。由此可见，与不考虑弹性模量变化的情况相比，考虑地基黏土层弹性模量变化时路基表面两桩中心处黏土沉降量的计算值更接近现场监测沉降量。

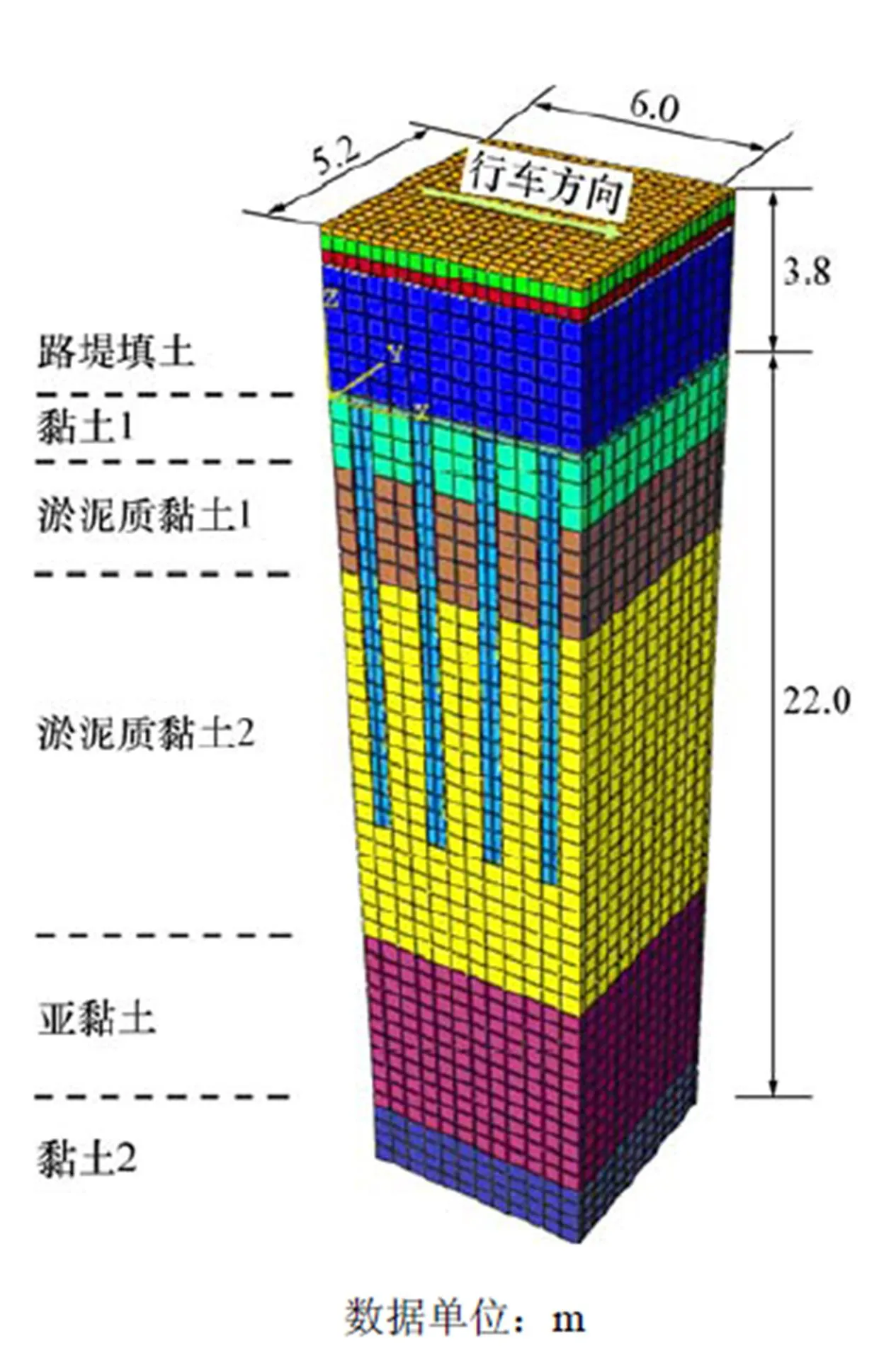
图7 有限元模型示意图

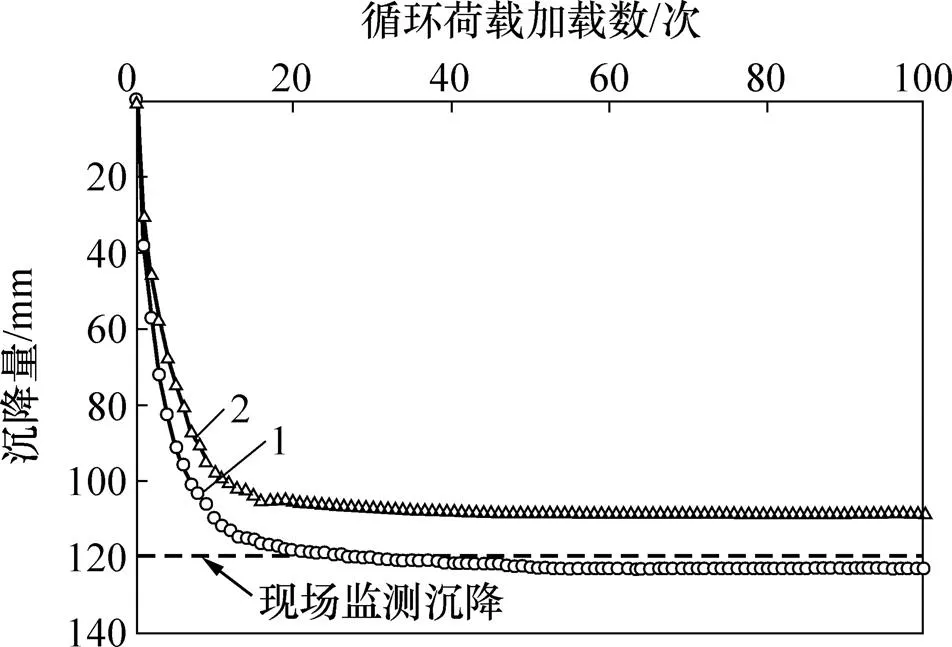
1—E变化；2—E恒定。

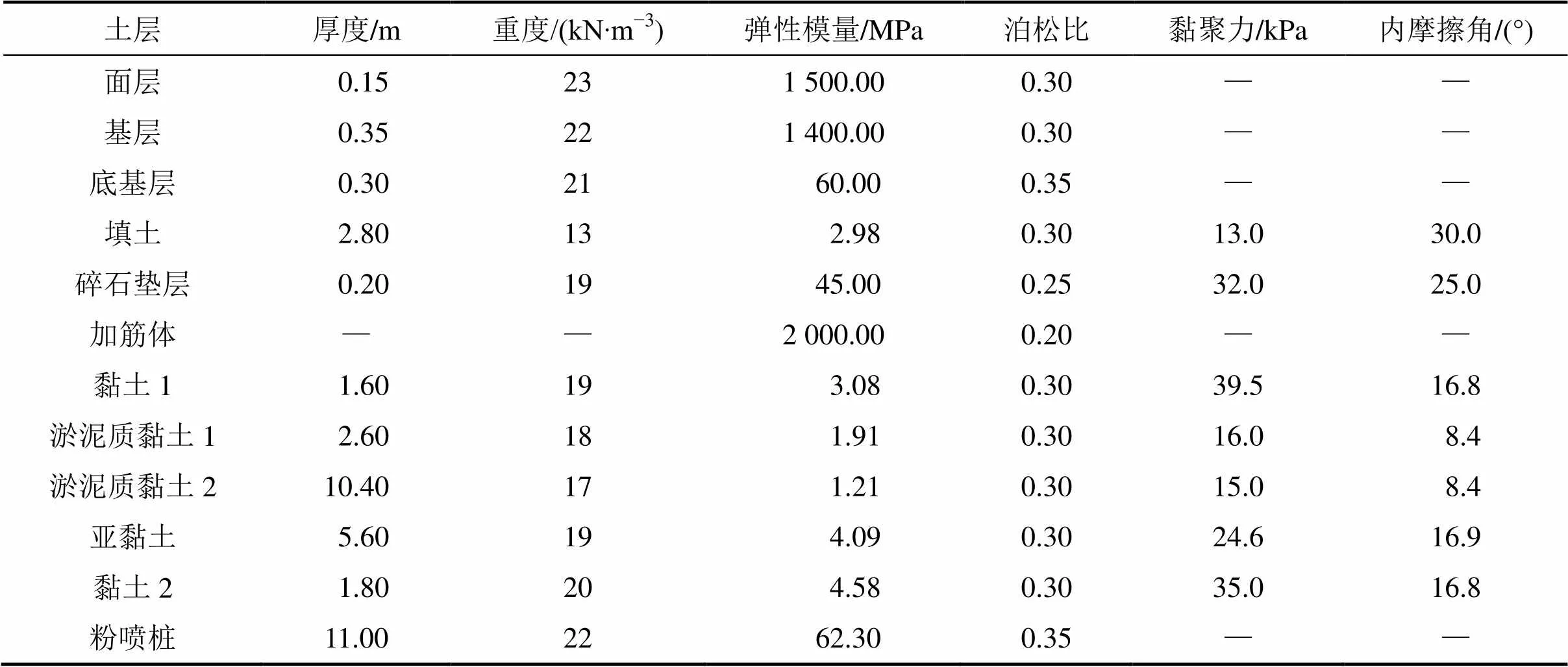
表3 模型参数

5 结论

1) 当动应变d相同时，围压越大，动弹性模量d越大；当动弹性模量d相同时，围压越大，动应变d越大；随着动应变d增大，动弹性模量d初期急剧减小，后期逐渐趋于平缓。

2) 当动应变d相同时，超固结比越大，动弹性模量d越大；当动弹性模量d相同时，超固结比越大，动应变d越大。

3) 不同孔隙比条件下得到的动弹性模量d与动应变d关系曲线趋于重合，孔隙比对动弹性模量d的影响较小。

4) 与经典Hardin−Drmevich公式相比，新的修正动弹性模量公式对试验结果的拟合效果更好。

[1] 沈珠江. 软土工程特性和软土地基设计[J]. 岩土工程学报, 1998, 20(1): 100−111. SHEN Zhujiang. Engineering properties of soft soils and design of soft ground[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(1): 100−111.

[2] 张磊, 高玉峰, 王军. 飞机荷载作用下温州机场超固结软粘土地基变形研究[J]. 三峡大学学报(自然科学版), 2013, 35(3): 59−64. ZHANG Lei, GAO Yufeng, WANG Jun. Study of deformations of Wenzhou airport over-consolidated soft clay foundation under cyclic aircraft loading[J]. Journal of China Three Gorges University, 2013, 35(3): 59−64.

[3] 刘升传, 王连俊, 丁桂伶. 高速铁路CFG桩复合地基柔性载荷试验研究[J]. 工程地质学报, 2008, 16(6): 813−819. LIU Shengchuan, WANG Lianjun, DING Guiling. Flexible or rigid loading tests for bearing capacity of CFG pile composite foundation along high-speed railway[J]. Journal of Engineering Geology, 2008, 16(6): 813−819.

[4] 贾宁, 陈仁朋, 陈云敏, 等. 杭甬高速公路拓宽工程理论分析及监测[J]. 岩土工程学报, 2004, 26(6): 755−760. JIA Ning, CHEN Renpeng, CHEN Yunmin, et al. Theoretical analysis and measurement for widening project of Hang—Yong expressway[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(6): 755−760.

[5] 叶耀东, 朱合华, 王如路. 软土地铁运营隧道病害现状及成因分析[J]. 地下空间与工程学报, 2007, 3(1): 157−160. YE Yaodong, ZHU Hehua, WANG Rulu. Analysis on the current status of metro operating tunnel damage in soft ground and its causes[J]. Chinese Journal of Underground Space & Engineering, 2007, 3(1): 157−160.

[6] HARDIN B O, DRNEVICH V P. Shear modulus and damping in soils: measurement and parameter effects[J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1972, 98(SM6): 603−624.

[7] 汪明元, 单治钢, 王亚军, 等. 应变控制下舟山岱山海相软土动弹性模量及阻尼比试验研究[J]. 岩石力学与工程学报, 2014(7): 1503−1512. WANG Mingyuan, SHAN Zhigang, WANG Yajun, et al. Dynamic elastic moduli and damping ratios of marine sediments at Zhoushan Daishan based on dynamic triaxial tests under strain control[J]. Chinese Journal of Rock Mechanics & Engineering, 2014, 33(7): 1503−1512.

[8] 徐毅青, 唐益群, 任兴伟, 等. 地铁振动荷载作用下隧道周围加固软黏土动弹性模量试验[J]. 工程力学, 2012, 29(7): 250−255. XU Yiqing, TANG Yiqun, REN Xingwei, et al. Experimental study on dynamic elastic modulus of reinforced soft clay around subway tunnel under vibration loading[J]. Engineering Mechanics, 2012, 29(7): 250−255.

[9] 刘飞禹, 蔡袁强, 徐长节, 等. 循环荷载软土动弹性模量衰减规律研究[J]. 浙江大学学报(工学版), 2008, 42(9): 1479−1483. LIU Feiyu, CAI Yuanqiang, XU Changjie, et al. Degradation of dynamic elastic modulus of soft clay under cyclic loading[J]. Journal of Zhejiang University(Engineering Science), 2008, 42(9): 1479−1483.

[10] 邱成春, 张孟喜. 水平−竖向加筋饱和砂土动弹性模量试验研究[J]. 岩土力学, 2012, 33(6): 71−76, 106. QIU Chengchun, ZHANG Mengxi. Test research on dynamic elastic modulus of saturated sand reinforced with horizontal-vertical inclusions[J]. Rock & Soil Mechanics, 2012, 33(6): 71−76, 106.

[11] 郑刚, 霍海峰, 雷华阳, 等. 振动频率对饱和黏土动力特性的影响[J]. 天津大学学报(自然科学与工程技术版), 2013, 46(1): 38−43. ZHEN Gang, HUO Haifeng, LEI Huayang, et al. Contrastive study on the dynamic characteristics of saturated clay in different vibration frequencies[J]. Journal of Tianjin University(Science and Technology), 2013, 46(1): 38−43.

[12] 李又云, 谢永利, 刘保健. 路基压实黄土动力特性的试验研究[J]. 岩石力学与工程学报, 2009, 28(5): 1037−1046. LI Youyun, XIE Yongli, LIU Baojian. Experimental research on dynamic characteristics of roadbed compaction loess [J]. Chinese Journal of Rock Mechanics & Engineering, 2009, 28(5): 1037−1046.

[13] 廖红建, 肖正华, 刘健. 动载下饱和重塑黄土的骨干曲线变化研究[J]. 岩土力学, 2011, 32(2): 375−379. LIAO Hongjian, XIAO Zhenghua, LIU Jian. Study of variation of backbone curve of saturated remolded loess under dynamic loading[J]. Rock & Soil Mechanics, 2011, 32(2): 375−379.

[14] DARENDELI M B. Development of a new family of normalized modulus reduction and material damping curves[D]. Austin, USA: University of Texas at Austin, 2001: 54−104.

[15] 李校兵, 谷川, 蔡袁强. 循环偏应力和循环围压耦合应力路径下饱和软黏土动模量衰减规律研究[J]. 岩土工程学报, 2014, 36(7): 1218−1226. LI Xiaobing, GU Chuan, CAI Yuanqiang. Dynamic modulus degradation for soft saturated clay under coupling stress paths of cyclic deviatoric stress and cyclic confining pressure[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(7): 1218−1226.

[16] 刘家顺. 高速铁路粉质粘土地基静、动力特性及沉降规律研究[D]. 北京: 辽宁工程技术大学土木与交通学院, 2015: 66−71. LIU Jiashun. Research on the static and dynamic characteristic of silty clay and the settlement law of subgrade of high speed railway[D]. Beijing: Liaoning Technical University. College of Civil and Transportation Engineering, 2015: 66−71.

[17] JTG E40—2007, 公路土工试验规程[S]. JTG E40—2007, Test methods of soils for highway engineering[S].

[18] TB 10102—2010, 铁路工程土工试验规程[S].TB 10102—2010, Code for soil test of railway engineering[S].

[19] 谢定义. 土动力学[M]. 北京: 高等教育出版社, 2011: 218−263. XIE Dingyi. Soils dynamics[M]. Beijing: Higher Education Press, 2011: 218−263.

[20] HARDIN B O, DRNEVICH V P. Shear modulus and damping in soils: design equations and curves[J]. Geotechnical Special Publication, 1972, 98(118): 667−692.

Analysis of factors affecting dynamic modulus of elasticity of saturated silty clay and research on backbone curve model

ZHUANG Yan1, 2, ZHU Wei1, 2, ZHANG Fei1, 2

(1. Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering, Hohai University, Nanjing 210098, China; 2. Geotechnical Research Institute, Hohai University, Nanjing 210098, China)

In order to study the change rules of the dynamic modulus of soil under traffic load, cyclic triaxial tests were performed on typical Southeast coast soft clay. The influences of confining pressure, consolidation ratio and void ratio on the dynamic elastic modulus were studied. Based on the classic Hardin−Drmevich equivalent linear model, a modified Hardin−Drmevich formula of dynamic elastic modulus considering both void ratio and consolidation ratio was developed. The results show that in the same strain level, dynamic elastic modulus increases with the increase of confining pressure and over-consolidation ratio. When the void ratio increases, the dynamic elastic modulus decreases. Compared with the conventional Hardin−Drmevich formula, the proposed formula is more suitable for the fitting of experimental result.

saturated silty clay; dynamic elastic modulus; dynamic triaxial test; modified Hardin−Drmevich model

10.11817/j.issn.1672−7207.2019.02.025

TU435

A

1672−7207(2019)02−0445−07

2018−03−16；

2018−05−16

国家自然科学基金资助项目(51478166)；“青蓝工程”资助项目(2016)；中央高校基本科研业务费专项资金资助项目(3205008801)；江苏高校优势学科建设工程资助项目(1105007138)(Project(51478166) supported by the National Natural Science Foundation of China; Project(2016) sponsored by Qinglan Program; Project(3205008801) supported by the Fundamental Research Funds for the Central Universities; Project(1105007138) supported by the Priority Academic Development Program of Jiangsu Higher Education Institutions)

庄妍，博士，教授，从事软土地基加固和路面安定性分析等研究；E-mail：Joanna_zhuang@163.com

(编辑 伍锦花)