基于CFD的对转螺旋桨水动力性能分析
2019-03-07孙承亮赵江滨
孙承亮,赵江滨
(1. 武汉理工大学 能源与动力工程学院,湖北 武汉 430063;2. 国家水运安全工程技术研究中心可靠性工程研究所,湖北 武汉 430063)
0 引 言
当今AUV的应用越来越广泛,涉及军事应用、地质勘探、考古等多个领域。其中推进系统是AUV的重要组成部分,它不仅与AUV的快速性和机动性有关,还关系到AUV的续航力[1]。如今螺旋桨推进仍然是AUV主流的推进形式,其中对转螺旋桨(Counter-Rotating Propellers)属于组合推进器中的一种,它不仅具有较高的效率,而且前后两桨的扭矩可以相互抵消,具有较高的稳定性,因此将对转螺旋桨应用在AUV上具有一定的实际意义[2–3]。
对转螺旋桨的前后两桨同轴且转向相反,其两桨的流场存在很大的相互干扰。本文基于CFD方法对AUV的对转螺旋桨进行水动力计算,分别运用SolidWorks和Ansys ICEM进行建模和网格划分,并分析计算结果,得到最佳湍流模型。运用最佳湍流模型来计算,对对转桨的最佳配合参数展开研究,并分析其尾流的变化规律。
1 螺旋桨基本参数
本文的计算模型为MAU型4叶螺旋桨,其主要参数如表1所示。对转桨由2个MAU型单桨组成,其基本配合参数包括桨距比L/D(两桨0.7 R处的轴向距离与螺旋桨直径的比值,L表示两桨0.7 R处的轴向距离,R表示螺旋桨半径,D表示直径)和直径比Da/Df(后桨直径与前桨直径的比值,Da为后桨直径,Df为前桨直径),L/D和Da/Df的变化对对转桨的性能有重要影响。

表 1 MAU螺旋桨基本参数Tab. 1 Basic propeller parameters
2 CFD计算原理
2.1 控制方程及湍流模型
数值模拟的是螺旋桨在一定来流速度的水中匀速旋转,在轴向上没有位移,把流体看作不可压的,则流场的连续性方程和动量方程[4]为:

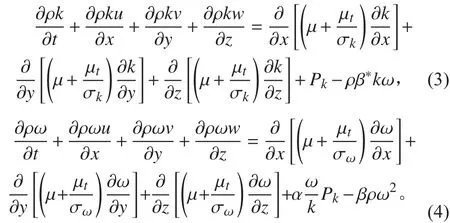
其中湍流动能生成项Pk为:
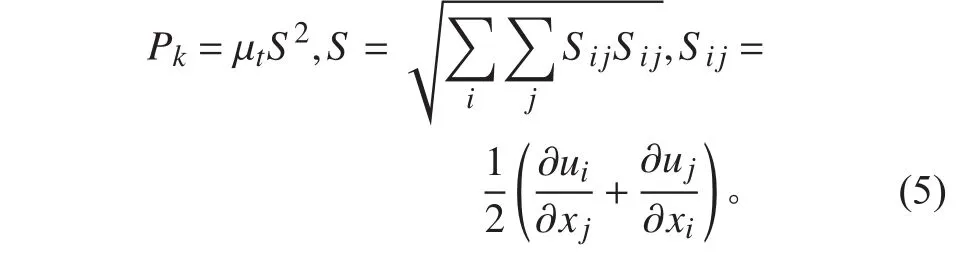
2.2 对转桨计算公式
根据1957 ITTC标准公式[6],得到对转桨的计算公式如式(6)~式(8):

3 计算方法及最佳湍流模型的选择
3.1 建模及网格划分
基于MAU型螺旋桨的二维型值点坐标,利用Excel函数将其转化为三维空间坐标,导入到Solidworks中生成桨叶曲线,依次通过填充曲面、放样、缝合等命令生成桨叶曲面,然后通过圆周阵列来生成其他桨叶[7]。最后根据毂径比绘制桨毂,得到完整的螺旋桨,如图1所示。

图 1 MAU型螺旋桨Fig. 1 The MAU propeller
本文选取的计算域为圆柱体,计算域模型在建模软件SolidWorks中完成,分为静止域和旋转域两部分[8–9]。静止域直径为6D,长度为10D,旋转域直径为1.2D,长度为D。利用ICEM进行网格划分,首先对静止域和旋转域单独划分网格,然后进行网格合并。静止域的几何形状为规则的圆柱形,故采用结构网格划分;旋转域的内壁面为螺旋桨的表面,曲率较大且几何形状较为复杂,只能采用非结构网格划分,对叶梢等尺寸较小的部分进行网格加密;然后利用ICEM中的merge命令将两者合并[10],得到总体网格及边界命名如图2所示。
3.2 最佳湍流模型
通过分析可以看出:对于推力系数KT,Standard模型和SST模型的误差较小,但是Standard模型的仿真值与试验值在J=0.7~0.8时出现交叉,说明计算值不够稳定;对于转矩系数KQ,可以看出随着J增大,各模型的误差都在增大,在J=0.7~0.8时SST的计算值与试验值贴合较好;对于敞水效率,在J=0.4~0.5时Standard模型的模拟效果最好,但总体来看,SST模型计算更稳定,可靠性更高,因此选择SST模型作为最佳计算模型。

图 2 网格划分及计算域设置情况Fig. 2 Grid division and computing domain Settings

图 3 不同湍流模型计算的敞水特性曲线Fig. 3 Open water characteristic curves calculated by different turbulence models
4 对转桨数值仿真及分析
本节主要探讨对转桨主要配合参数L/D和Da/Df的变化对对转桨的性能的影响,通过改变参数建立不同的对转桨模型,并进行仿真计算,得到最优结果。关于建模和网格划分与单桨基本相同,不同之处在于对转桨的前后2个桨单独建立旋转域。通过建模得到的对转桨模型如图4所示,网格划分情况如图5所示。

图 4 对转桨模型Fig. 4 The counter-rotating propeller model
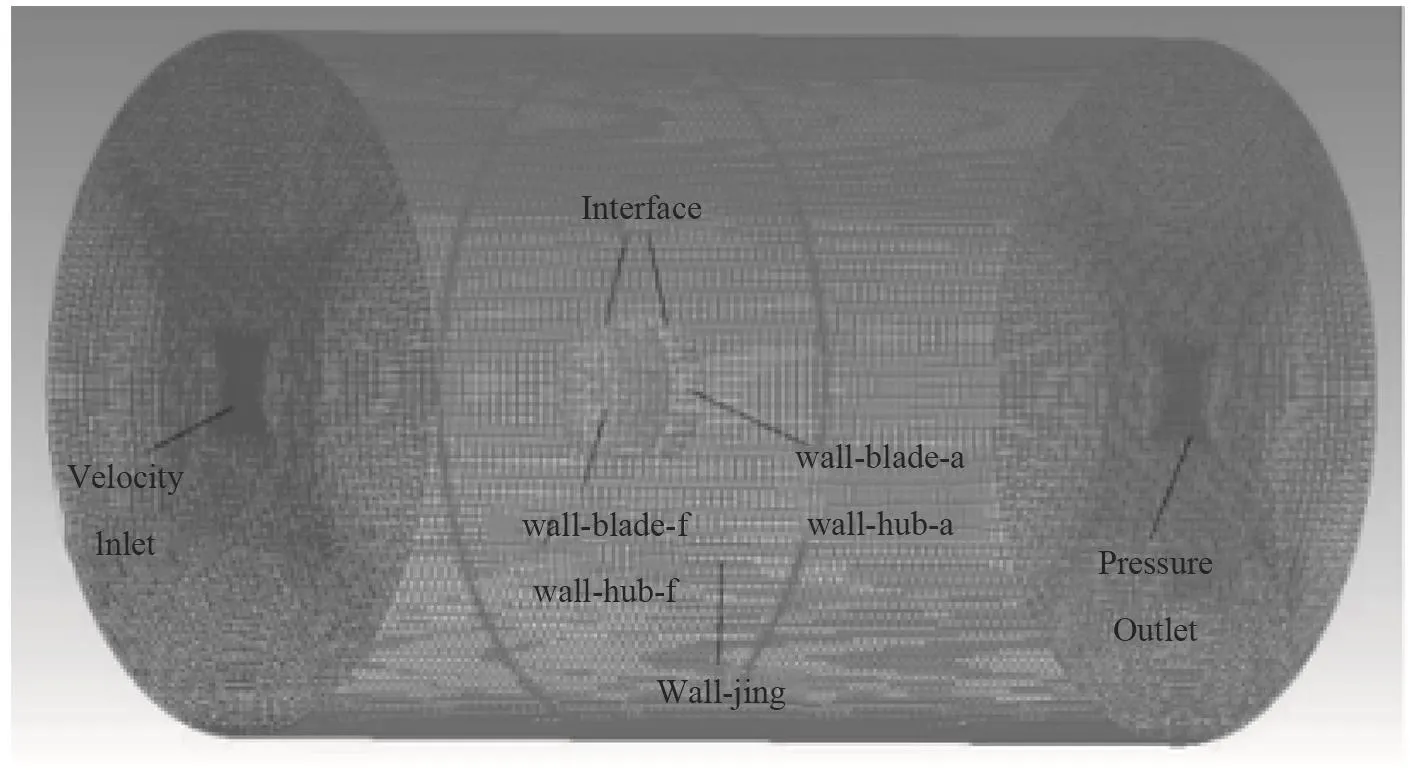
图 5 网格划分情况Fig. 5 Computational domain meshing
4.1 桨距比L/D最优值研究
在计算桨距比L/D时,先取两桨的直径Da=Df,对于Da/Df的最优值将在下一步中研究。为了确定最优桨距比,分别取L/D=0.233,0.267,0.283,0.300,0.333,对应不同的模型a,b,c,d,e。将计算结果表示为敞水性能曲线,如图6所示。

图 6 不同桨距比下对转桨敞水性能曲线Fig. 6 The open water performance curves of counter-rotatong propellers under different L/D
从图6可以看出,KT,KQ随着L的增加而增大,且逐渐趋于一个稳定值,可以推测当L足够大时,两桨就成为独立的单桨,其KT,KQ也不再变化。敞水效率先增大后减小,其中模型b的效率最高。分析其原因,当桨距过小时,前后两桨的尾流存在严重的相互干扰,导致前桨的叶面高压和后桨的叶背低压都不够充分,敞水效率也较低;当L增大到一个合适的值时,两桨均有各自足够的空间,后桨对前桨的尾流吸收率较高,且对前桨的影响也较小,此时敞水效率最高;当L继续增大时,由于距离增加,后桨能够吸收到的前桨尾流减小,敞水效率减小。综上所述,模型b的效率最高,即L/D=0.267时,对转桨的敞水效率最高。
4.2 直径比Da/Df最优值研究
采用控制变量法,选取不同的直径比作为变量,桨距比选择上一节中确定的最佳值,即取L/D=0.267。建立4组模型a,b,c,d,分别对应Da/Df=1.00,0.98,0.94,0.90。将计算结果绘制为敞水性能曲线,如图7所示。

图 7 不同直径比下的对转桨敞水曲线Fig. 7 The open water performance curves of counter-rotating propellers under different diameter ratio
可以看出,KT,KQ,都随着Da/Df的减小呈现出先增加后减小的趋势,其中模型c处的KT和值最大,模型b处的KQ值最大。分析其原因可能是,当后桨直径逐渐变小时,它刚好被前桨的尾流所包绕,从而效率较高。如果只考虑效率的话,模型c最佳,即Da/Df=0.94,但是考虑到公式的计算误差,模型c的后桨小于模型b,所以计算公式得到的模型c的值误差要大一点,此外模型b有最大的KQ,因此综合来看,取最佳Da/Df=0.94~0.98。
4.3 尾流分析
为了直观地反映对转桨前后桨之间的相互影响,利用后处理软件进行处理,做出了进速系数为0.6时各模型的流线图,如图8所示。
可以看出,模型a和模型b由于后桨直径较大,前桨的尾流线直径大于后桨,尾流发散比较严重,后桨吸收的效果不太好;对于模型c,前桨产生的尾流线直径与后桨比较接近,刚好把后桨充分包裹在内,前桨的尾流存在比较明显的收缩,这说明后桨对前桨的尾流吸收较好,效率较高,两者配合产生的水动力性能较好;对于模型d,可以看出其后桨的直径小于前桨的尾流直径,因此对前桨的吸收效率没有模型c高,结合上一节中分析的结果,选择最优直径比Da/Df=0.94。
4.4 对转桨与等效单桨性能对比

图 8 对转桨尾流线图(J=0.6)Fig. 8 The wake flow of counter-rotating propellers
对转桨有很多优点,其中最重要的一点就是与工况相同的单桨相比具有较高的效率。为了比较单桨和对转桨的效率,可以选择在相同的进速下比较,但是这样没有考虑螺旋桨的收到功率,也就是说在相同的进速下,两者的螺旋桨收到功率不同,这样得到的效率没有参考意义。这里选择转速n和螺旋桨收到功率P为定值,为了便于比较,引入功率系数Bp,在相同的Bp下比较两者的效率[11]。Bp表达式为:

关于单桨的选择,理论上应该选与对转桨等效的单桨,由参考文献知,在前后桨螺距相同的时,只需单桨的伸张轮廓面积与对转桨相同即可,即,其中AEO,AEf和AEa分别为单桨、对转桨前桨和后桨的伸张轮廓面积。通过计算可得到单桨模型的参数,如表2所示,对转桨的参数如表3所示。

表 2 等效单桨主要参数Tab. 2 The main parameters of the equivalent single propeller.

表 3 对转桨主要参数(模型c)Tab. 3 The main parameters of counter-rotating propeller
经过三维建模、网格划分和仿真计算,得到等效单桨的各水动力参数。结合对转桨的计算结果,可作出对转桨和等效单桨的Bp-曲线,如图9所示。为了便于比较,插值得到整数Bp值对应的两者的值进行比较,结果如表4所示。

图 9 对转桨和单桨的曲线Fig. 9 Thecurves of counter-rotating propellers and the single propeller

表 4 对转桨和单桨效率对比Tab. 4 Efficiency comparison of the counter-rotating propellers and the single propeller
由表4中数据可以看出,对转桨的效率比单桨的效率有较大的提高,最大时提升了9.307%,可以证明在相同的功率系数下,对转桨的效率比单桨更高。而CFD计算的结果存在5%的误差,因此理想状态下对转桨的效率提升可能会更高。
5 结 语
通过对MAU型螺旋桨和对转桨的水动力性能研究,得到如下结论:
1)基于RANS方程,计算得到螺旋桨的敞水性能,并与图谱试验值对比发现,Standard,RNG,SST三种湍流模型中,SST模型的计算误差最小,为最佳湍流模型。
2)通过CFD仿真计算,得到对转桨的最佳配合参数,L/D=0.267,Da/Df=0.94。尾流分析的结果也支持了得到的最佳桨距比和直径比的结果。
3)将对转桨和等效单桨的敞水性能在相同的功率系数下作对比,发现对转桨的效率比单桨最大提高9.307%,从而证明了对转桨的优越性。
