二维自由入反射波浪频域分离方法研究

杨 明

（中交第一航务工程勘察设计院有限公司，天津 300222）

引 言

在海工相关实验中，采集的波浪信号通常是入反射波叠加的合成波，这会对试验模型的水动力特性分析造成干扰。在工程实践中，近岸波浪发生反射后合成波的能量将明显增强，严重时可能破坏近岸结构物的稳定，同时不稳定的波浪场会影响港池内靠泊船只的作业效率，降低港口运营收益。所以，了解结构物反透射性能，掌握入反射波浪分离方法具有广泛的工程价值和理论意义。

当波浪行进至引起波浪产生的交变扰动力作用范围之外时，水体仅在重力和惯性力作用下继续传播的波动称为自由波[1]。入反射波的频域分离是指通过分析获得各成分波频谱密度的方法。相关研究始于1952年Healy[2]提出的单点法，该方法操作及原理简便，但适用范围和精度有局限。1972年Thomton[3]等提出了最早的频域分离，但其仅适用于规则波。目前为止应用和影响范围最广的适用不规则波分离的方法，是1976年Goda[4]提出的两点法和1980年Mansard[5]提出的三点法，与前者相比，后者基于二乘法最小平方和原理，应用时具有更宽的分析频域，减小了非线性项对计算精度的影响，同时对奇异解提出更严格限制。Isaacson于1991年建立了算法更为简便的三点法，不用计算相位差只需通过测点处的波高数据即可进行分离计算，但该方法对障碍物反射系数及测点布置间距的要求过于严格且计算精度有限，适用范围较小。1992年Zelt基于两点法和最小二乘法进一步优化互补，提出了布置多个测点的阵列法，既解决了两点法奇异解问题，同时通过对误差权重进行多重分配提高了计算精度。

这些早期成果为后来的波浪分离理论发展奠定了基础，后人分别提出了波浪斜向入射、变地形条件[6-8]、考虑水流影响[9]、波浪发生衰减[10]、非平稳波浪场[11]等基于不同应用条件的自由波分离方法。本文就典型方法的应用步骤和适用范围进行了梳理总结。

1 平坦地形

1.1 Goda两点法

两点法是指，在波浪行进方向上布置两个测点同步记录波形，利用 Fourier级数分析方法进行分离计算，可计算出总体反射系数及入反射波中不同频率间隔的成分波的幅值。

1）规则波分离计算原理

图1为浪高仪布置模型，基于线性波理论[12]，合成波中入、反射成分波的波浪时间序列：

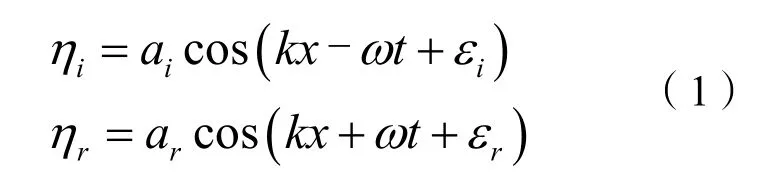
式中：

ai、ar表示入、反射波幅值；

波数k=2π/L，角频率ω=2π/T，k和ω满足线性色散关系方程ω2=gktanh2πkd；

εi、εr表示入、反射波初相。

x2=x1+Δx，测点采集序列作Fourier级数展开：

其中，A1、A2、B1、B2为Fourier系数。将上述两式联立结合测点记录的波形数据可得ai、ar：

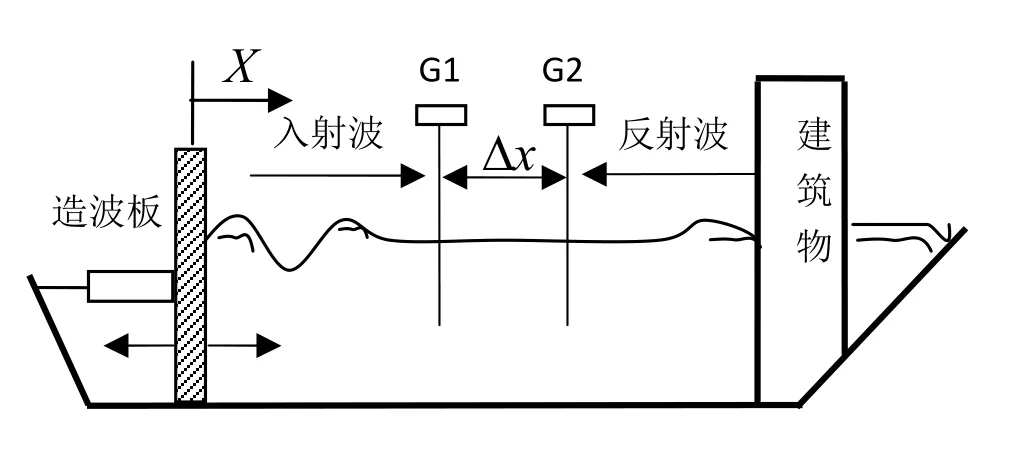
图1 两点法反射模型

2）不规则波分离计算原理

分离不规则波时，将其视为若干个频率间隔为Δf的规则波的线性组合。则各个成分波入反射波的波幅可表示为：

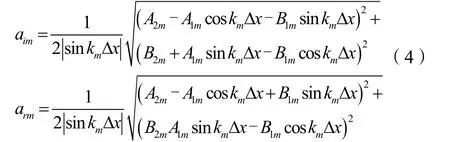
式中：km=2π/Lm，表示第m倍频成分波的波数；Lm=gT2m/2πtanh（2πd/Lm），为第m倍频成分波波长。

根据能量观点，合成波中总体反射率KR可表示为：

3）奇异性讨论

由式（3）、式（4）易知，当ΔxL=n2时，波幅表达式发散。对应情况：当浪高仪布置间距为1/2波长的整数倍时，两处将记录到的波形线相同只是相位差 π/2。Goda[4]给出的建议是：测点间距ΔxL分布在0.05～0.45范围里最理想。分离计算结果中有效成分波频率分布范围如图2所示。

两点法的3个假定条件：①波浪传播传播过程中不考虑横向波导致的波能损失；②将不规则波视为规则波的叠加；③各分频波的相速度相互独立。

图2 两点法分离波谱的有效范围

1.2 最小二乘法

Mansard等[5]建立了最小二乘法，布置不等距的三个浪高仪同步采集波形数据，分离频谱的有效宽度更广，计算过程中考虑了非线性项以及测波仪器中噪声误差的影响，分离结果精度更高。

1）分离原理

分离模型见图3，测点1（测点数p=3）处入反射合成波浪的时间序列表示：

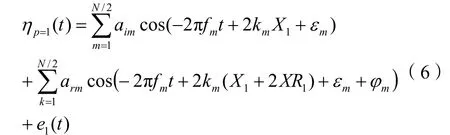
式中：φm表示反射作用导致的相位变化；e1（t）对应为误差项。其他测点的表达式同理。

图3 最小二乘法分离模型布置

将各点波面方程表达式作 Fourier变换可得到（X11=0）：

令：

整理上面两式，得：

2）奇异性讨论

最小二乘法奇异解的存在条件较两点法更为严格，对应等价为x12=nLm2，x13=mx12n。该方法应用时三个浪高仪的布置间距应满足以下条件[5]：x12=Lp2，Lp6≤x13≤Lp3，x13≠Lp5，x13≠3Lp10，Lp为谱峰频率分频波的波长。

图4 自由波频域分离流程

2 变地形情况

Chang和 Hsu[8]借助线性波浅水变形理论，分析由地形变化导致的波浪要素改变量，将两点法拓展到适用于变地形条件。

2.1 分离原理

数据采集与两点法相似，如图5所示，基于线性波理论，空间任意位置处的波浪时间序列可为：

图5 变地形条件下反射模型布置

基于线性波理论，浅水变形系数ks表示地形变化对波高的影响：

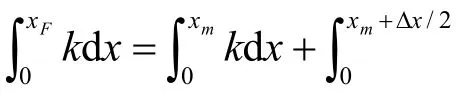
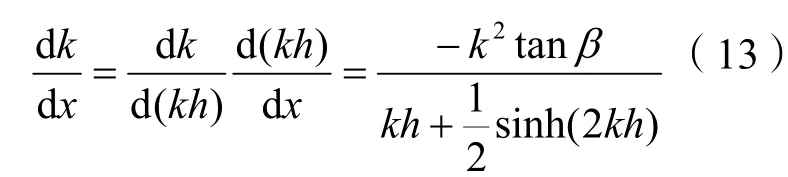
tanβ指倾斜度，水平条件，dk/dx=0，波浪行进时波数恒定，相位改变取决于测点间距；浅水条件，sinh2kh→2kh，dk/dx趋向-ktanβ/2h，变地形影响波数变化大；深水条件kh→0，dk/dx=0可理解为式（13）的分母无穷大，表明此条件下地形变化几乎不影响波数改变；整理前式，则xb和xf位置处波高可记为：

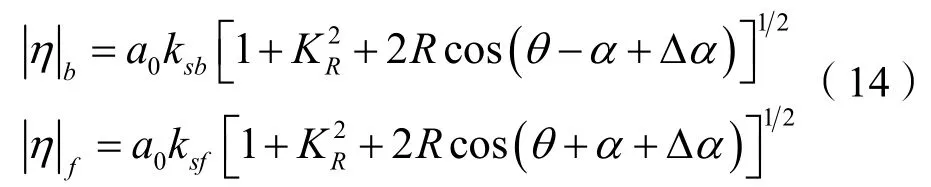
其中：

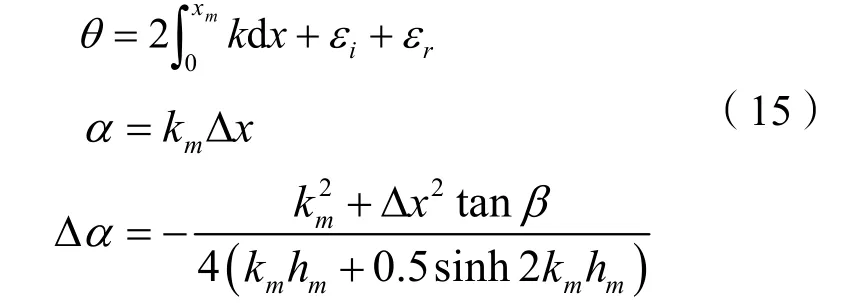
式（15b）指代测点间距带来的空间相位改变，式（15c）指代水深变化导致波数变化引起的相位改变。代换上式易得波浪反射系数为：

2.2 误差分析

2.3 奇异性讨论

2.4 不同水深不规则自由波的计算步骤

对于不规则波，可视为若干规则波（频率不同）线性叠加，利用FFT将测得波高转换为波能密度谱S（f），S（f）与波幅存在a（f）=[4S（f）df]1/2的转换关系。从所观测到波谱中转换出不同分频波幅值后依照式（16）可得出不同分频波的反射系数。

3 考虑水流

在工程实践中波流通常是共存的。Suh[9]借助Dopplor色散方程，建立了适用于考虑水流条件时入反射波的分离方法。计算分析模型同图 1，沿波浪前进方向布置测点p≥2，每个测点xp记录波浪时间序列可表示为：

在波流共存场中，入反射波浪的ki、kr变化而ω不改变。假设水流是稳定均匀流，方向垂直于波峰线，与入射波方向相同定义流速U为正，同理相反为负。则此时借助色散关系可得出：

结合三角变换及前文最小二乘法思想可导出：

波浪在静水区和水流存在区过渡时，受流速变化的影响波高、波长以及相对角频率rω变化而表视角频率aω恒定。所以该分离思想导出的波高值与静水条件对应的波高值存在如下转换关系（利用波作用量守恒方程易导出）：

4 结 语

本文总结了二维自由波频域分离方法，通过对其适用范围和计算方法进行梳理总结，得出以下结论：

1）频域方法的分离模型均源于两点法思想，基于线性波理论，考虑不同波浪环境下波浪运动参数（如波幅、波数等）受环境变化的影响，其中，波浪在水流中传播时通过Doppler色散关系计算波数，变地形条件下基于线性波理论中的波浪变浅系数计算不同水深处波幅值。

2）频域分离方法的奇异解存在条件、误差来源等特点一致，对于规则波，通过合理确定探针间距即可避免奇异解，对于不规则波，通过增加测点数可以提高计算精度。

3）上述方法是基于Fourier级数分析，将采集到的波浪时间序列进行时域内全局变换，此类方法的分离结果仅具备频率分辨率，所以频域方法适用规则波及平稳不规则波的分离。

4）若Fourier点数为N，时域内频率分辨率是不变的，不规则波被视为N/2+1个频率为n/T的规则波的叠加。考虑栅格效应，频率值非基频整数倍的分频波将被漏掉。因此N值取的越大，计算中取样的分频波与不规则波的实际组成波频率重合的部分越多，计算精度越高，但此举导致增加了计算机时，所以具体应用时，需考虑实际情况合理选取点数N值。