旋流导叶式生物质热解反应器内气固两相涡旋流动特性

2019-03-06张玉春易维明李志合王娜娜田纯焱

农业机械学报 2019年2期

张玉春易维明李志合付鹏王娜娜田纯焱

(1.山东理工大学农业工程与食品科学学院，淄博 255000；2.山东省清洁能源工程技术研究中心，淄博 255000)

0 引言

生物质催化热解是改善生物油品质、高效利用生物质资源的有效方法之一，生物质催化热解技术操作简便，只需在常压条件下即可实现，具有广阔的发展前景[1-3]。目前研究者普遍认为催化热解过程可以分成两步：一是生物质原材料在高温下生成热解气，二是在催化剂作用下热解气(主要是有机蒸气)进一步裂解成较小的分子，即发生催化裂解[4]。基于上述两步法发展了生物质原位催化热解和非原位催化热解两种技术，非原位催化热解与原位催化热解相比，由于可以根据两步反应特点有针对性地设计不同的反应器类型，且对于工艺条件改进和结构优化的研究可以根据不同反应特性分别开展，使其更具针对性、更加具体有效，因此非原位催化热解成为目前具有潜力和研究价值的新技术[5-6]。

目前文献报道的生物质催化裂解的常用反应器类型主要包括固定床反应器和流化床反应器[7-9]。在热解蒸气催化过程中，固定床反应器因结构简单、运行费用低，且对催化剂的强度要求不高，应用较多。但其暴露的缺点也越来越受到国内外研究学者的重视，包括反应器内部温度分布不均匀，传热差以及原料处理能力弱和催化剂无法更换等问题[10]，因此目前常用流化床反应器代替固定床反应器。与固定床反应器相比，流化床反应器易实现连续操作，且生产能力强，便于放大，但因存在环-核非均匀流动、流化介质与催化剂的分离以及逆重力场输送运行成本较高等问题[11-12]，在生物质催化热解中尚未广泛应用和推广。

文献[13-14]提出将涡旋流动场内反应分离一体化技术应用于生物质非原位催化热解工艺，其原理是：在涡旋流动场内生物质热解蒸气可通过旋转获得持续、稳定和可控制的离心力场，其巨大的剪切力和快速更新的相界面强化了热解蒸气这一气相与催化剂固相之间的相对速度和相互接触，从而实现高效的传质传热过程和化学反应过程，能够有效提高催化反应转化率，且离心力场被用于相间分离也是常用技术[15-16]。

基于上述指导思想，本文在顺流式旋风分离器的基础上设计一种新型旋流导叶式下行床反应器[17]，以提高催化裂解反应效率，并采用实验研究与数值模拟[18-20]相结合的方法，对旋流导叶式下行床反应器内气固两相涡旋流场进行分析，研究不同催化剂粒径、剂气比对反应器内气固梯度分布特性、分离特性以及催化剂停留时间分布的影响规律。

1 实验装置

该反应器结构如图1所示，入口到导向叶片上端为接触主反应区，在两个气相切向入口的引流作用下，该反应区形成弱旋流场，剪切力和快速更新的相界面强化了热解气与催化剂之间的相互接触，能够有效提高催化裂解转化率；导向叶片下部到排气管上端为反应分离耦合区，此时因存在大量气相热解产物，受到导向叶片的导流造旋作用，在强旋流场内主要进行的是各产物和催化剂因密度不同的分离过程，以及少量的催化反应和过裂解等副反应。

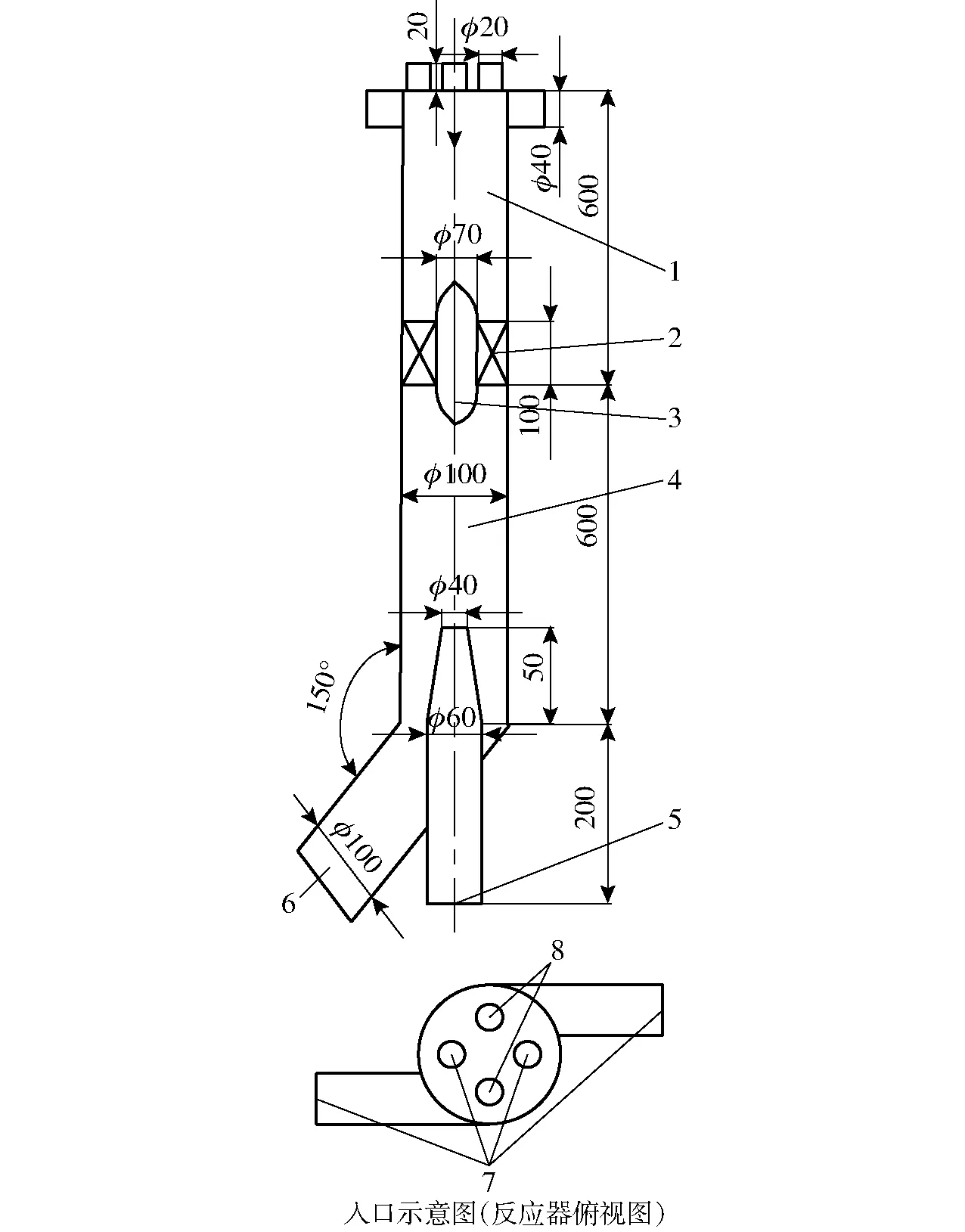
图1 旋流导叶式下行床反应器结构示意图Fig.1 Structure diagram of vortex downer reactor with guide vanes1.接触主反应区 2.导向叶片 3.导流锥 4.反应分离耦合区 5.排气口 6.排剂口 7.生物质热解蒸气进口 8.催化剂入口

实验装置主要由喂料系统、催化剂循环装置、反应器本体及测量系统4部分组成，如图2所示。实验装置采用有机玻璃材质进行冷态实验，可以对反应器内三维速度场及浓度分布进行测量，测量系统利用粒子图像测速法(Particle image velocimetry， PIV)技术[21-22]并配置七孔球探针测速系统和PV-6A型颗粒浓度测量仪[23]。

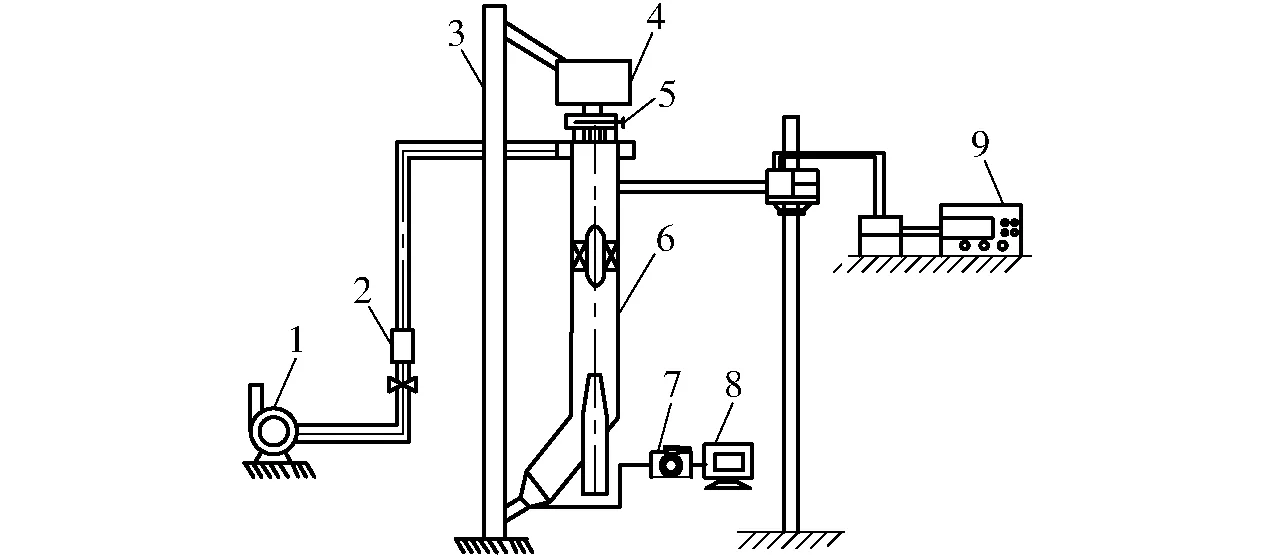
图2 实验装置示意图Fig.2 Experimental set-up1.风机 2.流量计 3.催化剂循环装置 4.催化剂箱 5.催化剂流量调节阀 6.反应器 7.高速摄像机 8.计算机 9.PV-6A型颗粒浓度测量仪

生物质催化裂解这种非均相反应体系中，两相接触效果越好，反应进行得越完全，但是时间过长，副反应则增多。而催化剂的停留时间分布(Residence time distribution, RTD)是评价反应器内气固相间接触时间的重要参考依据，对于正确把握物料在反应器内的混合情况和反应时间、增加产物收率、提高反应选择性、反应器过程强化与放大具有重要意义[24-26]。本文采用高速摄影、脉冲示踪法结合图像灰度化处理技术对停留时间进行实验测量[27]。停留时间的具体测量方法为：使用染色剂将部分催化剂进行染色作为示踪剂，在装置运行平稳后由入口处一次性注入少量示踪剂，同时在反应器出口利用高速摄像机获取图像监测示踪剂浓度，然后将其随时间变化处理为每隔0.025 s的逐帧图像，因采用黑色染色剂，故可采用Matlab将其处理为灰度图像，从而得到各图像的像素特征值，即对应于出口处各时间点的示踪剂浓度变化情况，进而最终得到RTD曲线。

停留时间分布函数指的是在某一停留时间下出口处示踪剂含量占示踪剂总量的比值，定义为

(1)

式中C(t)——出口示踪剂含量

t——时间

示踪剂的平均停留时间tm定义为

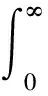
(2)

方差计算公式为

(3)

2 几何与数学模型

2.1 几何模型与网格划分

模拟采用的下行床反应器的几何结构如图1所示，计算坐标系采用直角坐标系，坐标原点设在接触主反应区顶端中心，Z轴沿轴向向下。根据结构化网格优于非结构化网格的原则，除入口和导流锥附近区域结构复杂采用四面体网格外，反应器其余区域均采用六面体网格，在验证了网格无关性基础上，最终确定网格节点数为 33万，图3是反应器网格示意图。

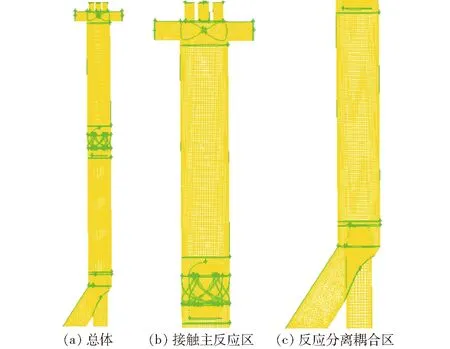
图3 反应器网格结构示意图Fig.3 Mesh diagrams of reactor

2.2 湍流模型

采用RNGk-ε[28]湍流模型，RNGk-ε模型与标准k-ε模型相比，修正了湍动黏度，考虑了平均流动中的旋转及旋转流动情况，故RNGk-ε模型可以更好地处理高应变率及流线弯曲程度较大的流动。

该模型中k和ε的输运方程分别为

(4)

(5)

其中

式中ρ——流体密度

Uj——流体速度k——湍动能

xj——x在j方向分量

ε——湍流耗散率

μeff——有效粘度

σk——与湍动能相关的普朗特数,取0.717 9

Gk——湍动能的产生项

σε——与湍流耗散率相关的普朗特数,取0.717 9

μ——流体动力粘度

μt——流体湍动粘度

η——应变率

β——热膨胀系数

Sij——用户定义源项

Cε1、Cε2——关于湍流耗散率的常系数

Cμ——关于流体粘度的常系数，取0.085

η0——应变率标准值，取4.28

2.3 数值求解和边界条件

以计算流体力学软件Fluent为平台，使用有限体积法建立离散方程，除压力梯度项的离散采用PRESTO[29]格式外，控制方程其他各项的离散均采用QUICK差分格式，并采用SIMPLE[30]算法进行数值求解。在下行床反应器内气体与催化剂形成气固两相流，并将催化剂视为拟流体，两相模型选择混合模型，反应器入口设为均匀速度入口，出口为充分发展的管流条件，气固无滑移边界条件[31]，其他参数设置如表1所示，其中入口速度和体积分数由实验测得的物料质量流量换算得到。

表1 参数设置Tab.1 Parameters of numerical simulation

3 计算结果及分析

3.1 模拟结果准确性验证

将空气与催化剂两相冷态流场模拟中的固相体积分数计算结果与利用PV-6A型颗粒浓度测量仪测量结果进行对比。如图4所示，图中r为同一截面以中心位置为圆心的径向距离，R为半径，r/R表示径向不同位置。由图可见，在z=300 mm和z=800 mm截面，实验值与模拟值基本重合，吻合较好。总体来看，模拟结果与实验结果有较好的一致性，证明采用该数值模拟方法对旋流导叶式生物质热解反应器内流场有良好的预测精度。因此在以下的数值模拟中仅将气相物质改为生物质热解蒸气，气相入口温度为500℃，其他边界条件等设置均不改变。

图4 实验与数值模拟固相体积分数对比Fig.4 Comparison of numerical and experimental data of solid concentration

3.2 涡旋流动场特性

图5分别是反应器接触主反应区和反应分离耦合区横截面的速度矢量分布图。相同点是速度方向均为顺时针，表明反应器内呈现涡旋流动形态，不同点是z=300 mm截面的速度明显小于z=800 mm截面，这与设计时的初衷也是相符的，接触主反应区的弱旋流场能够增强两相接触效果，而反应分离耦合区的强旋流场则是为了提高分离效率。

图5 不同横截面速度矢量图Fig.5 Velocity vector of different cross sections

图6是不同位置截面的催化剂固相体积分数分布云图。从图上可以看出，z=300 mm截面各部位的固相体积分数梯度较小，说明催化剂从入口进入反应器后在气相湍动以及固相颗粒之间的碰撞接触作用下迅速扩散到各处，对气相起到较好的催化作用。到达z=800 mm截面时，强旋产生的离心力使各组分因密度不同而逐渐分离，图上可见催化剂的固相体积分数梯度显著增大，中心大部分区域基本为零，具体数值将在下文中详细论述。

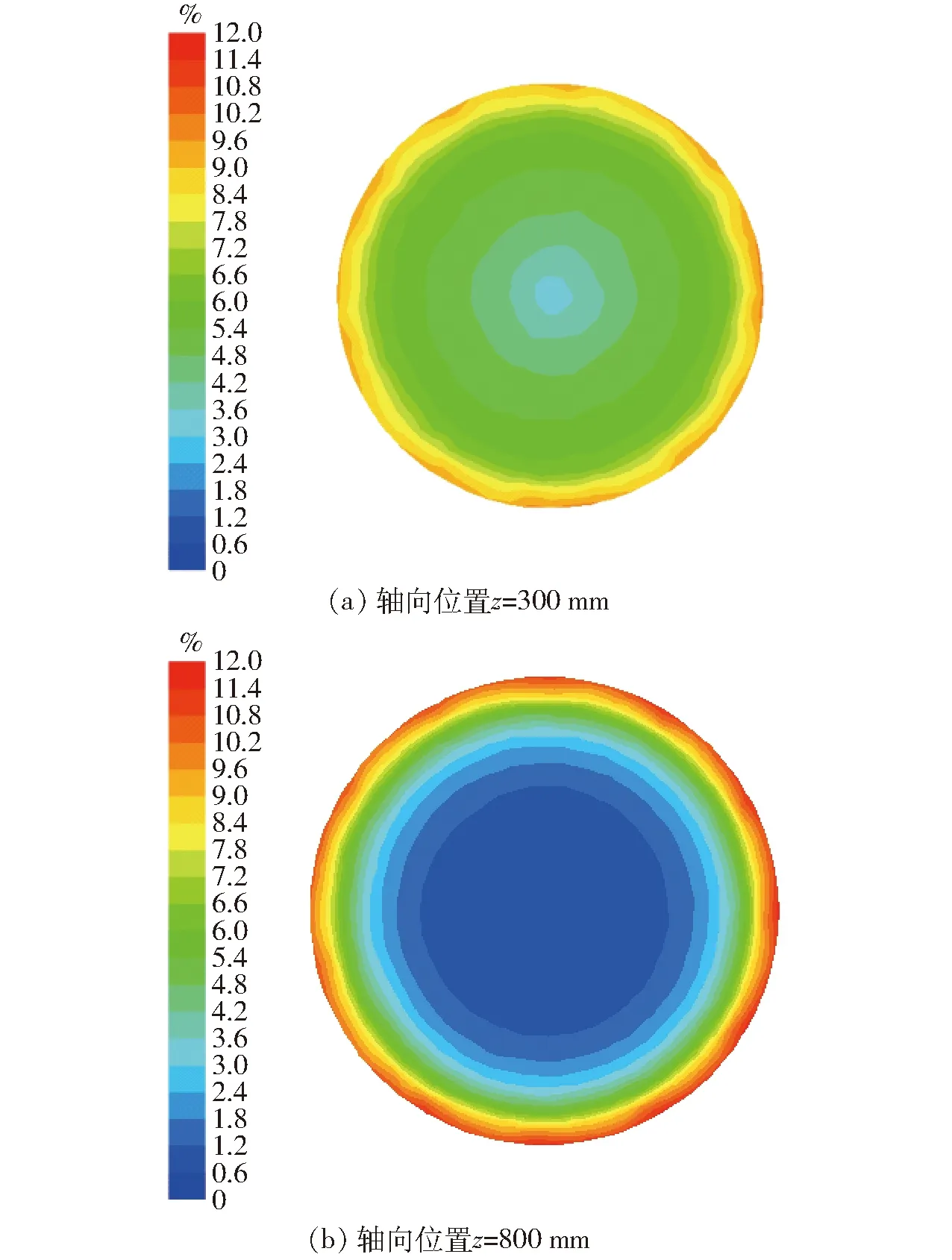
图6 不同横截面固相体积分数分布云图Fig.6 Solid holdup distributions at different cross sections

如图7所示，气相由切向入口进入反应器后形成一定的螺旋下行流，经过导向叶片后旋流强度增大且最终由排气口离开反应器，也有少量由排剂口流出。固相催化剂颗粒由轴向入口竖直向下进入后在气流作用下扩散并下移，经过导向叶片后在较强离心力场作用下沿边壁螺旋下行，最终由排剂口离开反应器，实现了催化剂与气体产物的分离。

图7 气固相运行轨迹示意图Fig.7 Schematic of gas and solid phase trajectories

3.3 颗粒粒径对固相体积分数分布的影响

催化剂颗粒粒径对于其能否有效扩散到反应器内各处以及反应后的分离效果影响非常大。因此将颗粒粒径为5、10、20 μm的算例分别定义为情况1、情况2、情况3，考察颗粒粒径对固相体积分数分布的影响规律。

图8 不同粒径下各截面固相体积分数分布曲线Fig.8 Solid holdup distribution curves of each section under different particle sizes

图8a是5 μm粒径颗粒在反应器内不同轴向位置截面的固相体积分数分布曲线。由图可见，催化剂由轴向入口进入反应器后z=50 mm截面梯度较大，r/R=0.4位置处出现高峰，r/R=-0.5位置处出现区域小高峰，这是由于该处位于竖直催化剂入口正下方，催化剂聚集程度大，而后跟随气流在下移过程中逐渐扩散，梯度有所减小，在弱旋流作用下两侧边壁附近浓度高于中间区域。到达z=500 mm截面，即接触主反应区末端时浓度分布明显改善，说明颗粒达到了有效扩散效果。

当颗粒粒径为10 μm时，由图8b可见沿轴向梯度固相体积分数逐渐减小，在z=100 mm截面已有明显改善，到达z=500 mm截面时催化剂体积分数集中分布在4%～8%之间，梯度明显减小，达到了较好的均匀扩散效果。

20 μm颗粒因粒径较大，受到的曳力作用也较大，因此从图8c可见在z=50 mm截面催化剂明显集中在轴向竖直入口正下方以及边壁附近，与中间部位浓度差别较大，而后催化剂颗粒的分布情况基本相同，都是边壁附近颗粒集中，中间部位基本为零，这是因为颗粒粒径最大，所受离心力也最大，即使在弱旋流动下也已呈现出较好的分离效果，且由于颗粒粒径较大、聚集程度较高，颗粒间的相互碰撞和磨损也最为剧烈。这种现象对于提高反应器的整体催化热解效率是不利的。

选取各轴向截面催化剂体积分数曲线上具有代表性的10个不同位置点计算其不均匀度Mes，公式为

(6)

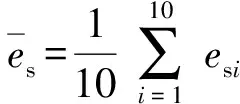
(7)

式中esi——同一高度曲线上第i点的固相体积分数

如图9所示，整体来看，3种催化剂粒径条件下催化剂的分布都是沿轴向下移不均匀度逐渐减小，但是，从数值上来看，情况2在各截面的不均匀度分布都低于情况1和情况3，优势明显。

图9 不同粒径下各截面不均匀度分布Fig.9 Histogram of heterogeneity distribution of each section under different particle sizes

图10是3种粒径催化剂z=800 mm截面的固相体积分数分布对比曲线。情况1中催化剂分离效果最差，中间大部分区域的固相体积分数在2%～4%之间，明显高于其他两种粒径。情况2中在z=800 mm截面中心大部分区域固相体积分数小于2%，仅在r/R>0.8区域数值明显增大。情况3与情况2的不同之处在于其中心大部分区域的固相体积分数在0～4%之间。综合图8、9的分析结果，当颗粒粒径dp=10 μm时催化剂在接触主反应区达到了较好的均匀扩散效果，保证了与生物质热解蒸气的充分接触，最终达到增强催化作用效果的目的，不均匀度在3种粒径条件下最低；在反应分离耦合区强旋造成的离心力作用下颗粒显示出较好的分离效果，保证了催化剂与反应后的产物快速分离，减少了二次反应的发生，从而能有效提高反应转化率。因此dp=10 μm为最优催化剂粒径。

图10 z=800 mm截面不同粒径下固相体积分数对比曲线Fig.10 Solid holdup comparison curves of catalysts with different particle sizes on section of z=800 mm

3.4 剂气比对固相体积分数分布的影响

通过改变入口气固相速度的方式来实现剂气比(催化剂循环量与进料质量之比，Catalyst to gas ratio，CTG)的变化，在情况2的基础上增加情况4和情况5，剂气比以及入口气固相速度如表2所示。

如图11a所示，由于剂气比最大，在z=50 mm截面可见催化剂明显集中在轴向竖直入口正下方，在z=100 mm和z=300 mm截面可见反应器内由上到下各截面颗粒体积分数梯度不断减小，在接触主反应区的弱旋流作用下，分布曲线基本为“U”形。到z=500 mm截面时，中心部位的固相体积分数均大于2%，边壁处约为9.5%。

表2 气固相入口速度对比Tab.2 Comparison of gas and solid phase inlet velocity

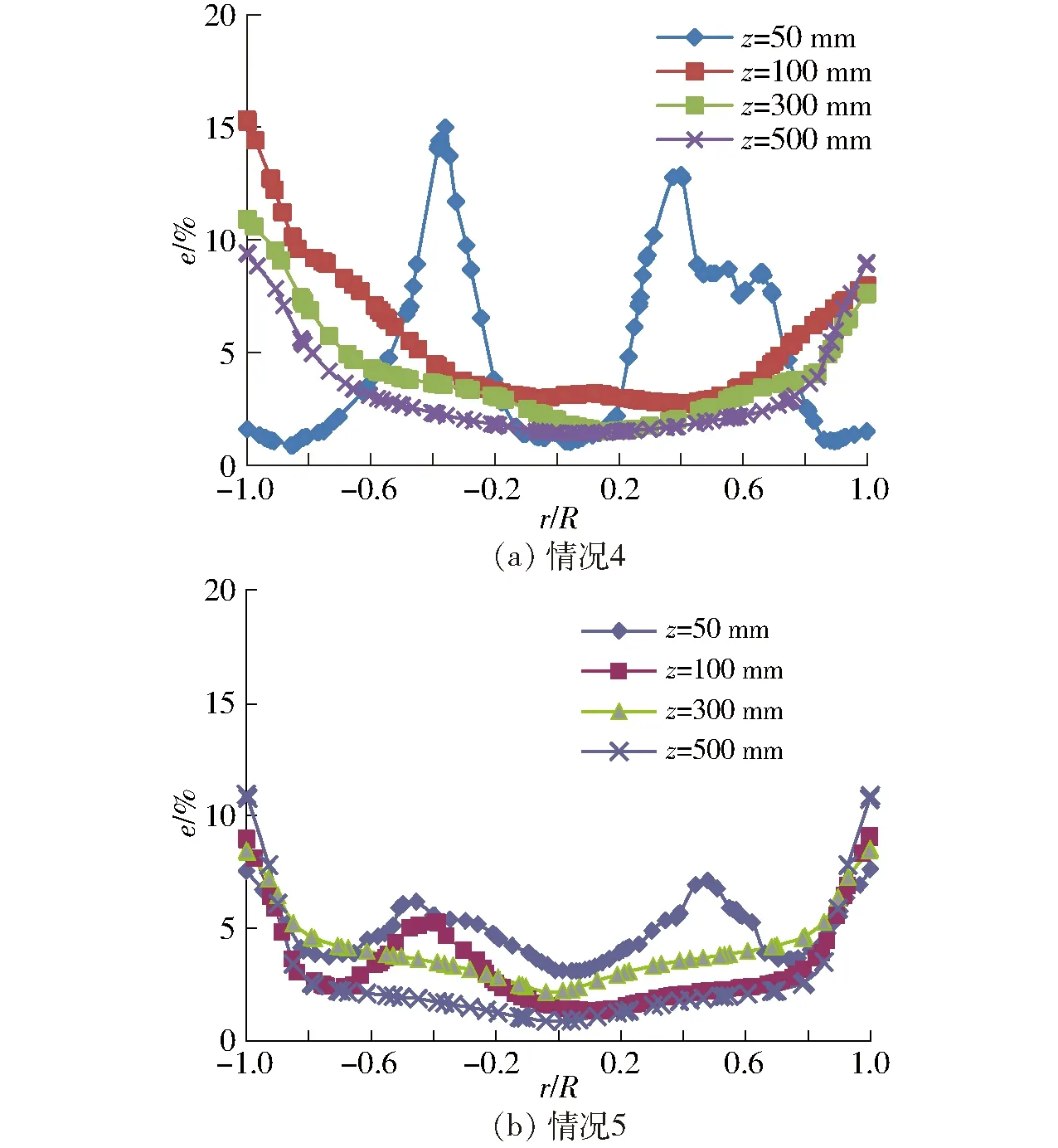
图11 不同剂气比下各截面固相体积分数分布曲线Fig.11 Solid holdup distribution curves of each section under different CTG

减小剂气比时，催化剂受到的曳力作用较小，从图11b也明显可见z=50 mm截面的固相“双峰”分布，而后在切向与轴向气流的湍流扰动作用下，催化剂迅速扩散到各处，浓度梯度减小，到z=100 mm截面仅在r/R=-0.4位置处和边壁处浓度稍高外，其余部位已基本达到均匀分布，在z=300 mm截面继续得到改善，由于剂气比小，气流旋流强度大，在z=500 mm截面催化剂颗粒已基本完成分离，中心大部分区域体积分数低于2%，如前所述，这种情况对催化反应不利。

从图12可见，情况4在各截面不均匀度都明显高于其他两种情况，而情况5虽然在z=50 mm和z=100 mm截面跟其他两种情况相比有较大优势，但在z=300 mm和z=500 mm截面不均匀度基本没有变化，导致最终不均匀度数值明显高于情况2。

图12 不同剂气比下各截面不均匀度分布Fig.12 Histogram of heterogeneity distribution of each section under different CTG

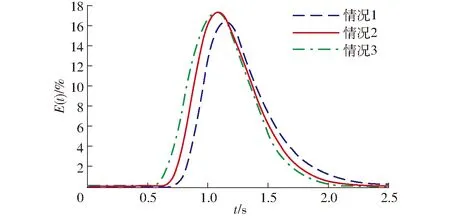
如图13所示，不同剂气比条件下的分离效果都较好，|r/R|<0.8范围内不大于2%，催化剂颗粒集中在0.8

图13 z=800 mm截面不同剂气比下固相体积分数对比曲线Fig.13 Solid holdup comparison curves of catalysts with different CTG on section of z=800 mm

综合上述分析结果，本文中剂气比最大(CTG为14.0)时催化剂在接触主反应区的体积分数梯度较大，不均匀度较高，而剂气比变小即催化剂活性中心减少，在发生裂解反应时气体体积仍持续增加，催化剂的失活程度会变高，单位催化剂上的积炭增多，因此会降低催化剂的催化作用强度，影响理想产物产率，综合考虑催化剂在热裂解反应中的活性中心数量和其与生物质热解蒸气的充分接触效果两方面因素，本文的最佳剂气比为10.5。

3.5 停留时间分布特性

实验测得不同粒径催化剂RTD曲线如图14所示。可以看出，催化剂颗粒RTD曲线呈现平滑的单峰分布，拖尾较小，三者的RTD 曲线整体差异小。5 μm粒径颗粒由于粒径最小，受到气相曳力作用也最小，因此易被卷入气流的涡旋运动中，产生颗粒的返混现象，从图上也可见其停留时间相比另外两种颗粒最长，但增加的比例很小，并没有对长周期平稳流动造成不良后果。而20 μm粒径颗粒与10 μm粒径颗粒的停留时间分布曲线差别非常小，20 μm粒径催化剂由于在三者中粒径最大，因此出现被气流携带进入次级流动的可能性也最小，故在图上可见其停留时间相对最小。

图14 不同粒径下RTD曲线Fig.14 RTD curves under different particle sizes

图15 不同剂气比下RTD曲线Fig.15 RTD curves under different CTG

如图15所示，剂气比为14.0(情况4)时，催化剂停留时间最长，这是因为剂气比最大，即催化剂所占比例在三者中最大，因此催化剂颗粒的轨迹分布形态也最丰富，结合前述结果可知该工况下在接触主反应区已近乎形成催化剂靠近边壁移动的运移形态，因此催化剂的流程最长，停留时间也最长；剂气比最小(情况5)时，由于固相体积分数最小，此时气相运动占主导地位，气流对于颗粒的作用效果最强烈，催化剂在气流的冲击携带作用下迅速离开反应器，因此其停留时间最短。

对RTD曲线进行分析，获得了不同工况下催化剂颗粒的平均停留时间，并根据公式计算得到无因次方差，如表 3 所示。由表 3 可知，平均停留时间为1.055～1.235 s。对于生物质快速催化热解工艺，催化剂会随着反应的进行而表面积碳导致活性降低，催化剂停留时间较短，有利于补给的新鲜催化剂与生物质热解气继续反应。另外，无因次方差对于催化剂颗粒的返混程度能够进行有效的判断。从表中可以看出，催化剂颗粒的无因次方差较小，接近于零，说明其流动接近平推流，进一步说明在新型旋流导叶式生物质催化热解反应器内，催化剂的输运、移出以及补给状态良好，能够满足生物质催化热解工艺的有序长周期平稳运行。