CWRF模式在中国夏季极端降水模拟的误差订正

董晓云 余锦华 梁信忠2) 马 圆

1)(南京信息工程大学气象灾害教育部重点实验室， 南京 210044) 2)(美国马里兰大学地球系统科学多学科中心， 马里兰 20740)

利用1980—2015年6—8月我国逐日降水观测数据评估CWRF模式(Climate-Weather Research and Forecasting model)多种参数化方案对我国夏季日降水的模拟能力，并考察累积概率变换偏差订正法(CDFt)的订正效果。通过将广义帕累托分布(GPD)引入到偏差订正模型中，提出针对极端降水的累积概率变换偏差订正法(XCDFt)，检验和评估其对极端降水订正的适用性。结果显示：CWRF模式微物理过程选用Morrison-aerosol参数化方案组合对我国降水场的模拟较好，CDFt订正效果良好；XCDFt偏差订正模型能够较好地提取模式建模与验证时期变化信号，订正后相比订正前与观测极端降水的概率分布更为接近；经过XCDFt订正后华南、华中和华北地区20年一遇的极端降水重现水平较模拟值更接近观测值，可为CWRF模式提高极端降水的业务预测水平提供参考。

引 言

近年来，在全球变暖背景下多发的极端降水事件对经济、社会、生命安全和生态环境系统等诸多方面造成了巨大影响，因此，极端降水事件的研究受到广泛关注[1-5]。极端降水作为小概率事件，一般具有强度大、存在突发性或转折性特点，导致极端降水的预报和评估有很多不确定因素。

相对于全球气候模式，区域气候模式具有更高分辨率、更为复杂的物理参数化方案，使模式对局地强迫引起的气候特征具有较好的模拟能力。随着区域气候模拟研究的不断深入，区域气候模式CWRF(Climate-Weather Research and Forecasting model)因为其优异性能开始被广泛应用[6-7]，然而，CWRF模式在区域气候的模拟也不可避免地存在一些偏差[6]。进一步完善物理过程和参数化方案是减小模式模拟偏差的一个比较直接的方法，同时，通过多模式集成，并结合统计偏差订正方法，是进一步降低模式模拟偏差的重要手段[8-11],这对得到更加准确的模拟结果、提高气候模式预估水平具有重要意义。

国内外学者围绕模式偏差提出了一系列的订正方法，从简单的线性变换到基于概率投影、天气随机发生器等相对复杂的办法[12-13]。其中基于概率分布函数的偏差订正方法较为常用，通过对比观测和模拟变量的累积概率分布函数构建传递函数进行订正(TF)[14-18]。依据累积概率分布函数和传递函数的不同，TF法又可以分为参数化和非参数化两种方案，主要包含基于概率分布的投影变换和基于经验累积概率分布函数的分位点投影等方法，本文分别采取经验累积概率分布函数对日降水、广义帕累托分布(GPD)对极端降水进行误差订正。

最新发展的CWRF模式已应用于国家气候中心业务预报试验，研究其极端降水误差订正效果，为提高CWRF模式对极端降水的业务预测水平提供参考，有重要的应用价值。

1 模式、数据和方法

1.1 模式和数据

Liang等[19-20]改进了WRF模式，进行了大量敏感性试验和严格的验证，完成了CWRF开发工作。CWRF模式采用兰伯特投影，网格距为30 km，纬向共232个格点，经向共172个格点。CWRF为每一个关键的物理过程(包括陆面过程(地面、河流)、行星边界层、积云对流过程、微物理过程、辐射过程等)集成了一套全面的交替参数化方案。模式从1979年10月1日开始，积分至2015年12月31日，共4个积分时段，考虑到模式需要一段时间进行初始化，实际采用1980—2015年6—8月日降水量数据。

本文采用CWRF控制方案Cl组合为基础[6]，C1微物理过程采用GSFCGCE参数化方案[21]，积云对流过程采用ECP&UW参数化方案[22-24]，每次单个置换C1中微物理和积云对流的参数化方案得到13套参数化方案[8](表1)。数据包括：①CWRF模拟的1980—2015年中国地区6—8月逐日降水量数据，选取控制方案和以上13种参数化组合方案一共14套模式数据。②1980—2015年6—8月中国2416个气象站的逐日降水量观测数据并插值到CWRF网格。将模式和观测数据统一划分为建模时期(1980—1996年)和验证时期(1997—2015年)。后者用于独立检验，评估偏差订正技术对模式模拟日降水和极端降水的改善性能。此外，模式将中国大陆分为11个区域[6],分别为华南、华中、华北、东北、内蒙古、藏东、西南、藏南、藏西、南疆、北疆。

表1 CWRF模式参数化方案Table 1 Parameterization schemes of CWRF

1.2 方 法

1.2.1 CDFt偏差订正

Michelangei等[36]提出基于经验累积概率分布函数的概率变换偏差订正法(CDF-transform，CDFt)。即存在转换函数T，满足

T(FXc(x))=FYc(x)。

(1)

(2)

假定式(1)在验证时期也适用，即T(FXp(x))=FYp(x),代入式(2)，得

FYp(x)=T(FXp(x))

(3)

其中，FXp(x),FYp(x)为验证时期模式模拟和订正后降水的经验累积概率分布函数。最后通过线性插值得到验证时期模式模拟降水的偏差订正值。

1.2.2 XCDFt偏差订正

XCDFt为Kallache等[37]在CDFt基础上的改进，不同于CDFt针对所有逐日降水数据，XCDFt针对于极值数据处理，并且引入GPD刻画其极值分布。其关系构建类似于CDFt(式(3))，不同的分布选择如下：假设FXc，FYc和FXp均服从GPD，FXc，FXp和FYc分别为模式建模和验证时期、观测建模时期超阈值降水的累积概率分布函数：

(4)

式(4)中，x为极端降水，u为阈值，σ是尺度参数，ξ是形状参数，本文采用可信度高的极大似然估计法对GPD的参数进行估计。

1.2.3 评估指标

1.2.3.1 布莱尔评分(Bs)、显著性评分(Ss)和均方根误差

Bs和Ss由基于每个格点降水序列的概率分布函数PDF求得，用于刻画模拟分布效果。假设Poi和Pmi分别为观测和模拟降水序列在第i区间的概率密度，n为分隔区间数量，则

(5)

(6)

由此可知，Ss指标是描述模拟和观测分布重叠程度的度量，而Bs描述的是两者之间分布不重合的程度。模拟和观测分布越接近，Bs指数的值越趋于0，Ss的值越趋于1。

1.2.3.2 极端降水的重现水平

重现水平是出现气候极值概率的气候变量的可能取值，出现极值概率的倒数就是重现期T。GPD重现水平的估计式为

(7)

式(7)中，k是超出阈值样本量与总样本量的比值，T是重现期。

2 日降水偏差订正及其效果评估

为检验14种不同参数化对中国区域降水分布总体模拟能力和订正效果从而选出一套模拟效果好并对订正有响应的数据做进一步研究，采用CDFt偏差订正模型对中国区域夏季日降水量进行订正，得到验证时期降水量的订正序列，并与同期降水量模拟数据和观测数据就日降水量及其概率分布等方面进行对比。

计算得到14套CWRF模拟夏季日降水以及CDFt订正后序列分别与观测日降水量在中国区域平均的布莱尔评分、显著性评分和均方根误差(图1)，将14套方案的评估指标联合排名(参见图2)。综合排名位于前3位的分别是C11,C14,C5组合方案(即Thompson，Morrison-aerosol，NSAS参数化方案)。计算表明：区域之间的评分各有不同，但华北、华中和华南3个区域总体的模拟和CDFt订正效果优于整体。全国来看，C14组合方案模拟效果最好，CDFt订正效果也较好，本文将选用该套方案进行极端降水偏差订正的研究。

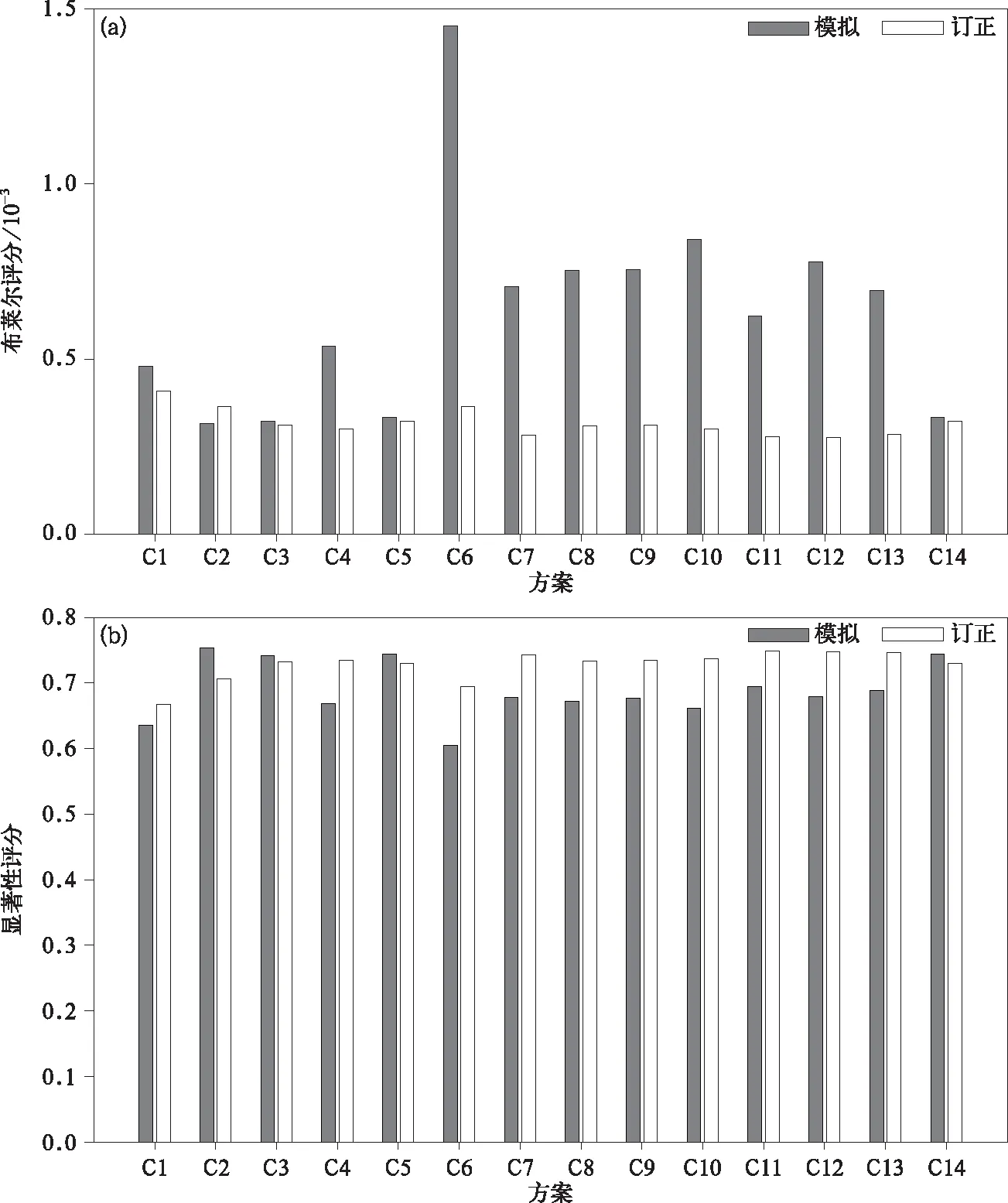
图1 不同参数化方案下中国区域CWRF模拟和CDFt订正日降水量对比(a)布莱尔评分，(b)显著性评分，(c)均方根误差Fig.1 Comparison of daily precipitation simulated by CWRF and corrected by CDFt over China under different schemes(a)Brier score,(b)significance score,(c)root mean square error

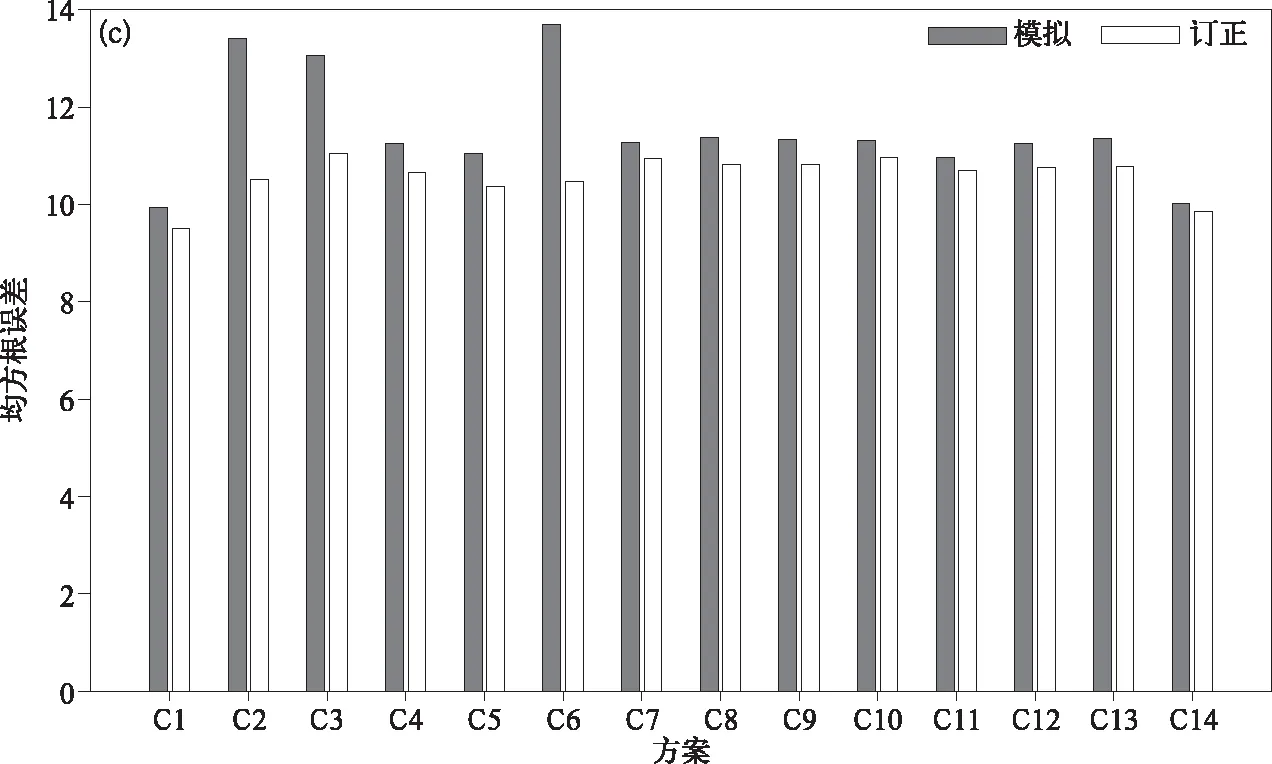
续图1

图2 不同参数化方案CWRF模拟、CDFt订正以及综合的日降水评估指标累计排名Fig.2 The cumulative ranking of evaluation indicators for different parameterized schemes of simulation,correction and comprehensiveness for daily precipitation

3 极端降水偏差订正及其效果评估

3.1 极端降水特征

XCDFt模型针对极端降水进行订正，阈值选择是获得和决定所需样本的关键，阈值选取合适与否会直接影响GPD拟合效果和XCDFt偏差订正。本文选取并计算了C14组合方案模拟和观测在验证时期(1997—2015年)的夏季逐日降水第95百分位数作为极端降水阈值，将阈值代入降水序列得到超阈值样本量(图3)。在验证时期，CWRF模式模拟阈值和观测的总体相近，但在华中部分地区的阈值小于观测所得阈值，这与模式多低值降水有关。新疆和西藏、云南等地区受其特殊地形和阈值选取方法的影响，两个时期超阈值样本均较高，模拟和观测的样本量差值较大，不利于订正。东南沿海地区3个区域，模式模拟阈值和超阈值样本量与观测相近，且极端降水出现概率高，危害大，故以下对于极端降水的空间订正选取华南、华中和华北。

3.2 极端降水订正及其效果评估

3.2.1 代表站的极端降水偏差订正及效果评估

XCDFt为Kallache等[20]在Michelangeli等[19]提出的基于累积概率分布函数概率变换偏差订正法(CDFt)基础上的改进，并成功应用于法国南部极端降水预报。为了评估XCDFt对CWRF模式模拟极端降水偏差订正的适用性，从华南、华中和华北选取经济发达且对极端降水灾害敏感的长沙、济南、南京、南宁4个地区为例，Xc，Yc表示建模时期(1980—1996年)模式和观测极端降水序列，Xp，Yp分别表示验证时期(1997—2015年)模式和观测极端降水序列，应用模式建模与验证时期极端降水Xc，Xp和观测建模时期极端降水Yc构建XCDFt模型，从而获得4个地区偏差订正后的极端降水，通过与验证时期观测极端降水Yp对比评估其订正效果。

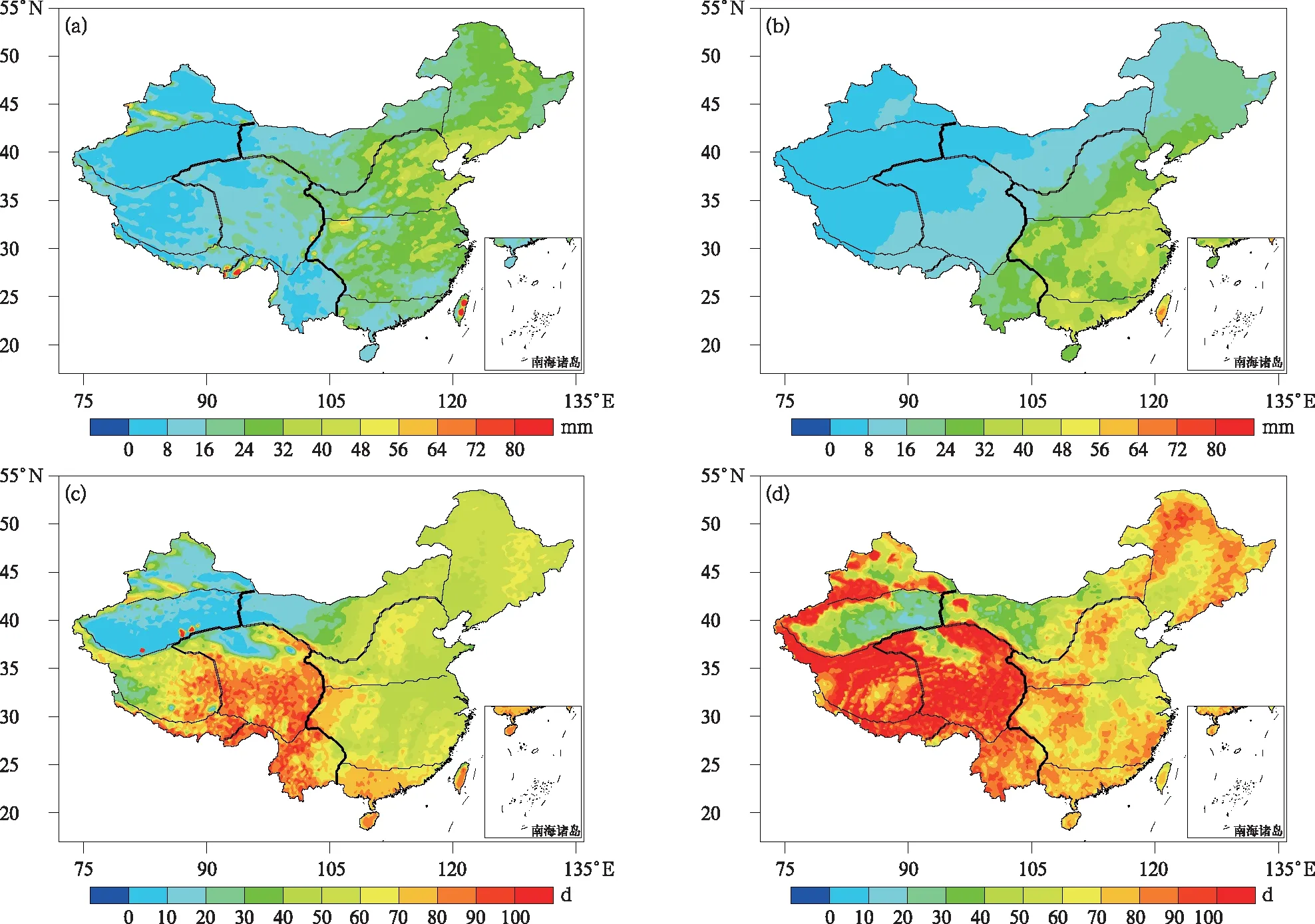
图3 验证时期中国夏季日降水量第95百分位数阈值及超过该阈值的极端降水日数(a)CWRF模拟阈值，(b)观测阈值，(c)CWRF模拟日数，(d)观测日数Fig.3 The threshold of the 95th percentile and the number of extreme precipitation days over threshold in summer during the validation period over China(a)simulated threshold by CWRF，(b)observed threshold,(c)the number of days simulated by CWRF，(d)the number of days observed

基于阈值数据筛选出每个气象站的极端降水序列，考虑到不同极端降水序列取值范围并不完全相同，为了获得验证时期极端降水偏差订正分布，往往需要对数据先进行平移和膨胀处理，使极端降水序列变化范围一致，再引进GPD对Yc，Xc，Xp，进行拟合。

在长沙、济南、南京、南宁代表地区，对建模和验证时期的极端降水及其分布模拟和订正诊断发现，GPD均能够较好地刻画各极值序列分布。图4示例南京地区XCDFt模型构建中验证时期观测极端降水序列GPD拟合的效果图。由图4可知，频率分布与GPD概率密度曲线相吻合，GPD可以较好地刻画其特征，其K-S分布检验结果也达到0.05显著性水平。

依据上述建模和验证时期模式与观测XCDFt分布拟合结果，得到验证时期偏差订正极端降水分布FYp和订正后的降水序列Yd。图5给出了4个地区模式建模和验证时期4个极端降水序列的分布函数以及应用XCDFt概率偏差订正后的分布FYp。可以看出，4个地区模式在建模和验证时期分布仅发生微小变化时，经XCDFt订正后得到的分布也对应发生较小变化;当模式数据与观测数据分布存在较大差异时，XCDFt订正依然会较好保留观测分布大部分信息并有效提取模式建模和验证时期累积概率分布函数变化特征信息。通过验证时期模式模拟和XCDFt所得偏差订正分布与观测验证序列的对比可以看出，对比模式模拟，订正后的序列分布在不同量级上均与观测分布更为吻合。经过订正，4个地区在极端降水低值部分的概率分布与观测明显更接近，中间部分略偏离观测序列的分布，一方面，是因为模式未较好地刻画出两个时期极端降水的变化；另一方面，与所选XCDFt阈值作为观测序列极端降水筛选有关，使用观测降水阈值，两者分布会更为接近。

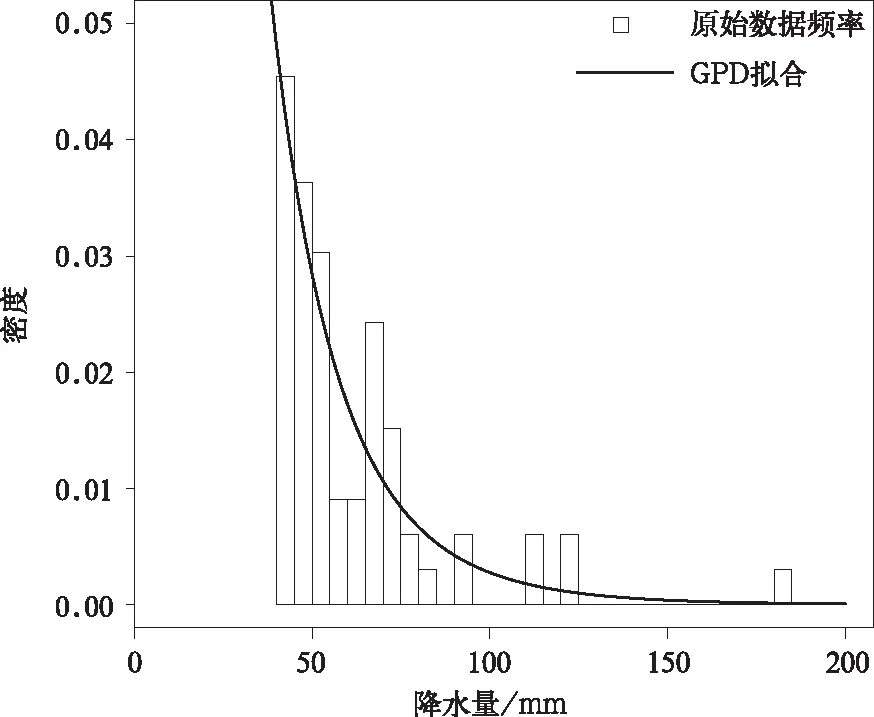
图4 南京站验证时期观测极端降水GPD拟合Fig.4 GPD fitting effect of the observed extreme rainfall during the validation period in Nanjing

图6给出了4个地区验证时期模式模拟序列、概率偏差订正序列和观测序列分布的分位点-分位点对应图，即Q-Q图。若模式降水与观测降水越接近，则其分位点也会越接近，图6中绘制的点也会越接近直线y=x，偏离直线的程度体现了模拟和订正效果的好坏。由图6可知，模式模拟的极端降水存在明显系统偏差，长沙、济南和南京地区模式较观测偏低，这点与模式模拟降水微量降水偏多、总体降水量值偏低有关。经过XCDFt偏差订正后，4个地区模式模拟降水得到了明显改善，长沙、济南、南京和南宁模拟和观测的极端降水平均值偏差率由订正前的8.75%，16.2%，14.7%，-14.6%经订正后降至-7.9%，8.6%，-2.3%，-2.0%，订正后数据更接近于观测。但不同量级的降水订正略有偏差，4个地区对于极端降水的低值部分(50 mm 以下)偏差订正效果较好，中间部分订正较差。南宁地区的偏差订正分位点分布基本与观测一致，总体而言，模拟较好地区的订正效果没有模拟较差地区的订正效果明显。

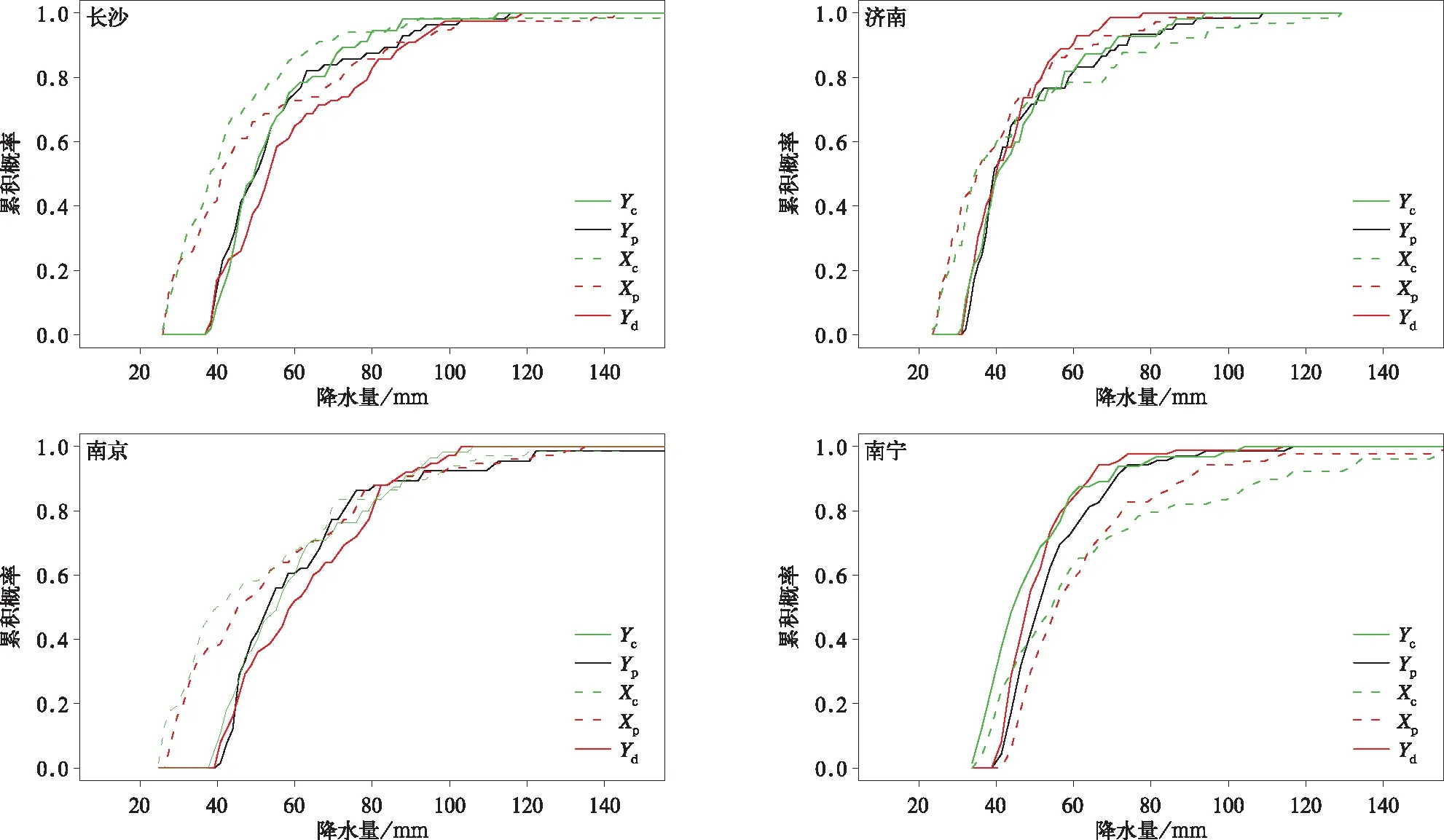
图5 建模和验证时期4个代表地区XCDFt偏差订正中CWRF模拟和观测夏季极端降水累积概率分布Fig.5 The cumulative probability distribution of extreme precipitation simulated by CWRF compared to observation in summer in the bias correction model XCDFt during the calibration and validation periods of four representation areas

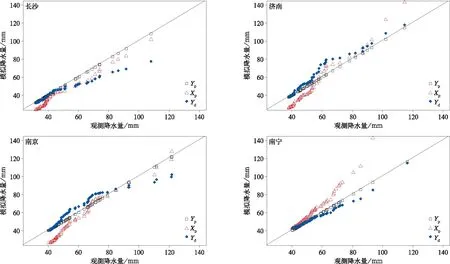
图6 验证时期4个代表地区XCDFt偏差订正中CWRF模拟和观测夏季极端降水Q-Q图Fig.6 Quantile-quantile plot of extreme precipitation simulated by CWRF compared to observation in summer during the validation period of four representation areas

3.2.2 订正前后极端降水重现水平的空间分布及效果评估

以华南、华中和华北极端降水重现水平分析XCDFt订正效果。给出了验证时期模式模拟、观测和模式订正后重现期为20年(图7)的极端降水重现水平。由图7可知，经过偏差订正后的重现水平与观测值更为接近。20年一遇的重现水平从模式订正前后和观测的空间均方根误差看，华南、华中和华北分别由73.677,48.500,47.170订正后下降至48.716,39.487,36.688，总体由52.422下降到40.090；从模式订正前后和观测的空间相关系数看，华南、华中和华北分别由0.320,0.388,0.449经订正后上升至0.497,0.423,0.492，总体由0.470上升至0.560；20年一遇的重现水平区域平均由订正前的113.66 mm降低到订正后的108.75 mm，与观测值102.89 mm更为相近，可见XCDFt对于订正极端降水重现水平效果良好。同时注意到极端降水重现水平在皖赣鄂、京津冀交界处的订正效果一般，可以发现模式模拟有极大值，20年一遇的重现水平都达到了200 mm·d-1以上，这些地区模拟的平均阈值和尺度参数σ较观测偏大，进而影响了XCDFt订正效果。

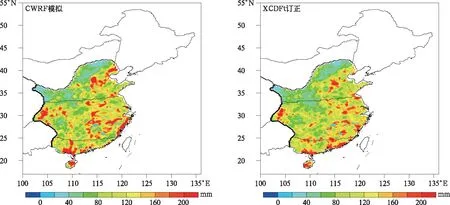
图7 验证时期华南、华中、华北地区极端降水20年一遇重现水平空间分布Fig.7 Spatial distribution of 20-year return level of extreme precipitation simulated,XCDFt corrected and observed over South China,Central China and North China during the validation period

续图7

4 结论与讨论

1) 通过CWRF 14套不同参数化方案在CDFt订正前后与观测的布莱尔评分、显著性评分、均方根误差的对比发现，微物理过程选用Morrison-aerosol参数化的C14组合方案对我国降水场具有较好的模拟和CDFt订正效果，该方案在华南、华中和华北地区对夏季逐日降水阈值和超阈值样本的模拟与观测相近。

2) 在长沙、济南、南京、南宁代表地区，对建模和验证时期的极端降水及其分布模拟和订正诊断发现，GPD能够较好刻画各极值序列的分布。XCDFt偏差订正模型能够较好地提取模式建模与验证时期变化信号，订正后相比订正前与观测验证极端降水概率分布更为接近，但不同量级的极端降水订正略有偏差。

3) XCDFt偏差订正模型可以较好地改进华南、华中和华北极端降水重现水平与观测数据的吻合度。经过XCDFt订正后的20年一遇的极端降水重现水平的空间平均值、均方根误差和空间系数相比模拟值与观测更为接近，订正后的数据更为可信，研究结果可以为CWRF模式准确预测极端降水事件提供参考。

误差订正仅能作为改进极端降水预测的辅助手段，模式物理过程的精细化描述、提高模式的分辨率等是提高极端降水预测水平的关键。本文重点关注极端降水出现频率较高的东南沿海3个区域，其他区域将进一步研究。