WEKA平台下的聚类分析算法比较研究

韩存鸽 叶球孙

(1. 武夷学院数学与计算机学院， 福建 武夷山 354300；2. 认知计算与智能信息处理福建省高校重点实验室， 武夷山 354300)

聚类分析是数据挖掘研究中一个非常活跃的研究领域。数据挖掘的一个重要任务是发现众多数据中的积聚现象，然后对其进行定量化描述。聚类分析是在对数据不作任何假设的条件下，用数学方法研究和处理所给对象的分类以及各类之间的亲疏程度，其目标是要将具有相似特征的样本数据归为一类，并使得类内差异小、类间差异大。聚类与分类不同。在分类模型中存在样本数据，这些数据的类标号是已知的，分类的目的是从训练样本集中提取出分类的规则，用于对其他类标号未知的对象进行类表示。聚类是在不知道目标数据的有关类的信息的情况下，以某种度量为标准将所有的数据对象划分到各个簇中。聚类分析因此又被称为无监督的学习[1]。聚类算法的目的是要寻找数据中潜在的自然分组结构和特定的关系。目前已经存在许多聚类算法。本次研究，将通过实验对几种常用的聚类算法进行比较分析。

1 常用的几种聚类算法概述

不同的聚类算法在进行决策树分析时存在一定的差异。评价聚类算法性能的指标主要有3个：一是正确预测的能力，即预测的准确率；二是可解释性，产生的有关模型要易于理解；三是速度，即产生规则的时间越短越好[2]。另外，与人工判断的吻合度是最直观的评判准则之一。在众多的聚类算法中，基于划分的K-means算法、基于模型的EM算法、基于密度的DBSCAN算法和基于分层的FarthestFirst算法是比较常用的算法，我们主要比较分析这4种聚类算法的性能。

1.1 K-means算法

1.1.1 K-means的原理及流程

1967年由J.B.Macqueen提出的K-means算法，目前已经成为数理统计、模式识别、机器学习和数据挖掘等领域应用最普遍的一种聚类算法，并有多种变形算法，组成了K-means算法家族。

按照K-means算法，先是进行粗略的分类，然后根据某种最优的原则修改不合理的分类，直到类分比较合理，形成最终的分类结果。因此，首先需要随机地选择k个对象，每个对象初始代表一个簇的平均值或中心。接着将剩余的每个对象，根据其与各个簇均值的距离，分派给最近的簇；然后计算每个簇的新均值。这个过程不断重复，直到准则函数收敛。通常采用平方误差准则，其定义如下[3]：

其中：p是空间中的点，表示给定的数据对象；mi是簇ci的平均值。

K-means均值划分算法的流程如下。

Input：K(簇的数目)，D(包含n个对象的数据集)

Output：K个簇的集合

方法：(1)从D中任意选择k个对象作为初始簇中心；(2)repeat；(3)根据簇中对象的均值，将每个对象指派到最相似的簇；(4)更新簇均值，即计算每个簇中对象的均值；(5)簇均值不再发生变化，则结束。

1.1.2 K-means应用举例

坐标上有5个点{x1，x2，x3，x4，x5}，进行聚类分析。5个二维样本为：x1=(0，0)，x2=(5，2)，x3=(1.5，0)，x4=(0，2)，x5=(5，0)。假设k=2。

Step 1：随机分为2个簇，计算质心M。

C1=(x1，x2，x3)C2=(x4，x5)

M1={0+5+1.5/3，0+2+0/3}={2.17，0.67}

M2={0+5/2，2+2/2}={2.5，1}

(2-0.67)2+(1.5-2.17)2+(0-0.67)2]=15.83

e2=15.83+14.5=30.33

step 2：计算质心到样本的距离，并取距离最小的重新分配到簇。

d(M1，x1)=[(0-2.17)2+(0-0.67)2]1/2=2.27

d(M2，x1)=2.69=>x1∈C1

d(M1，x2)=3.12

d(M2，x2)=2.69=>x2∈C2

d(M1，x3)=0.95

d(M2，x3)=1.414=>x3∈C1

d(M1，x4)=2.54

d(M2，x4)=2.69=>x4∈C1

d(M1，x5)=2.91

d(M2，x5)=2.69=>x5∈C2

step 3：根据重新分配的簇，计算新质心。

C1=(x1，x3，x4)C2=(x2，x5)

M1={0.5，0.67}M2={5，1}

相应的方差是：e2=4.166 7+2=6.166 7

第一次迭代后，总体误差显著减小(由30.33减小到6.166 7)，算法终止。

1.2 EM算法

EM算法(Expectation Maximization Algorithm)[4]是一种逐次逼近算法，包括计算期望值和求极大值，主要运用高斯混合模型的参数估计。该模型可以解决聚类分析、机器学习等领域中的许多实际问题。该算法的步骤如下：

Input：观测数据(y1，y2，…，yn)，高斯混合模型

Output：高斯混合模型参数

(1) 取参数的初始值，开始迭代。

(2) 求期望值。依据当前模型参数，计算lgP(y,γα|θ)的期望，即Q(θ,θ(i))=E[lgP(y,γ|θ|)|y,θ(i)]。

(3) 求极大值。求函数Q(θ,θ(i))对θ的极大值，即计算新一轮迭代的模型参数：θ( i +1)=argmaxQ(θ,θ( i))。

(4) 重复第(2)步和第(3)步，直至收敛，即直到对数似然函数值θ不再有明显的变化为止。

1.3 DBSCAN和FarthestFirst算法

DBSCAN(Density-Based Spatial Clustering Application with Noise)算法是一种经典的基于密度的聚类算法，用于过滤噪声数据，实现快速发现任意形状的类的分析[5]。执行流程：扫描数据库，找到每个点的邻居个数e。如果e大于阈限值，则该记录作为中心记录，随即以这个记录为中心的类就产生了[6]。DBSCAN算法使用欧式距离度量，确定哪些实例属于哪个簇。与K均值算法不同，DBSCAN算法可以自动确定簇的数目，发现任意形状的簇，并纳入离群概念。

FarthestFirst算法是快速地近似K均值的聚类算法，每一次取最远的那个点。该算法主要包括2个部分：FarthestFirst遍历和层次聚类。FarthestFirst遍历的思想类似于构造一棵最小生成树(针对点到集合)。算法过程如下[7]：

Input：n data points with a distance metric d(.,.)

Pick a point and label it 1

Fori=2,3,…,n

Fint the point furthest from {1,2,…,i-1} and label iti.

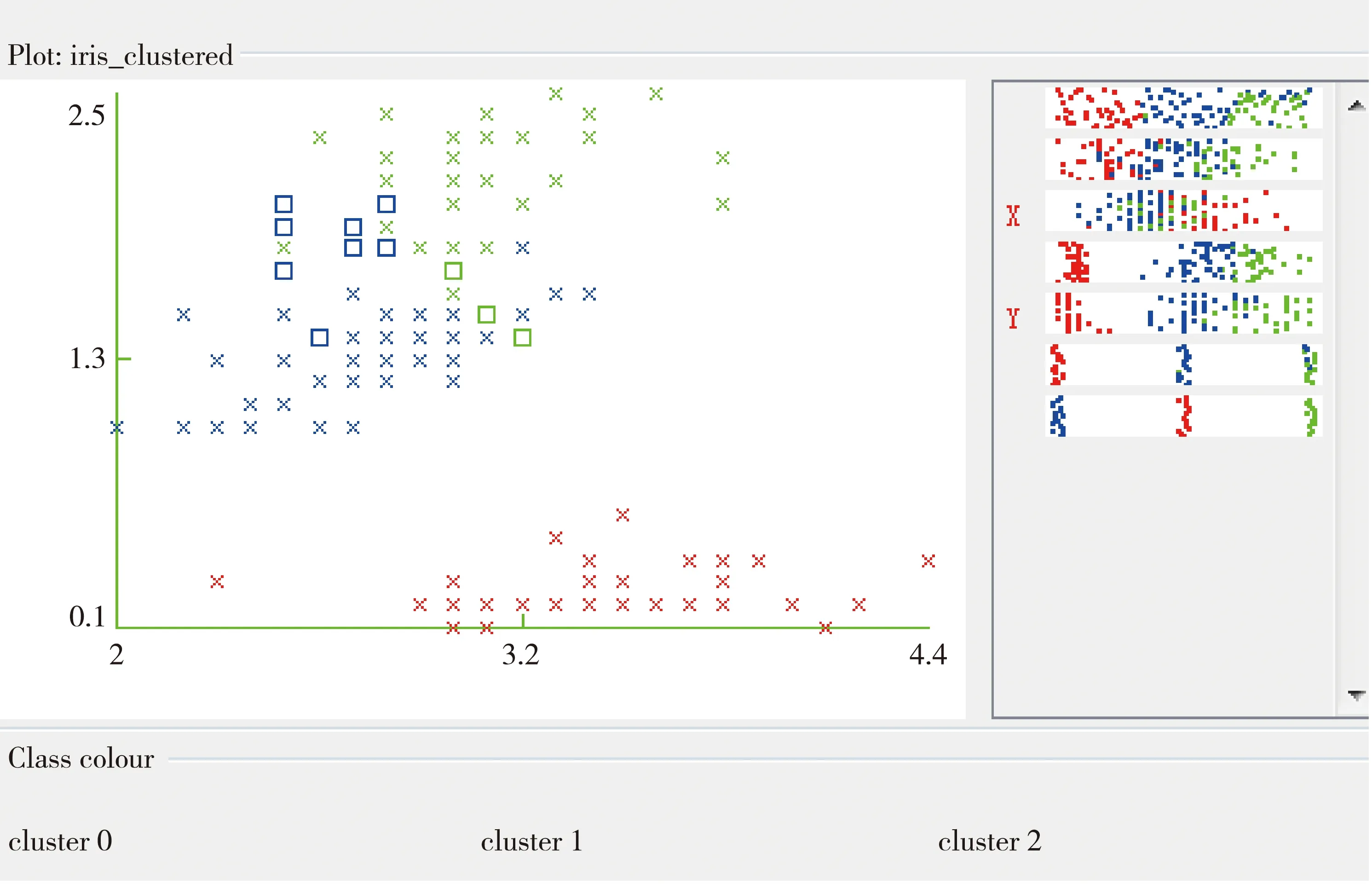
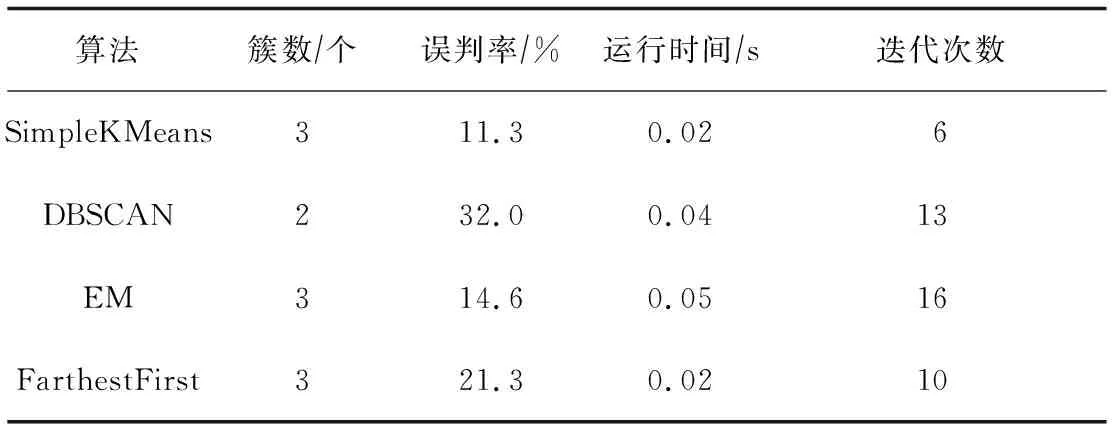
Let π(i)=argminj

LetRi=d(i,π(i))

2 WEKA平台下的聚类过程

怀卡托智能分析环境(Waikato Environment for Knowledge Analysis，缩写为“WEKA”)，是一种使用Java语言编写的数据挖掘机器学习软件，其中包括处理标准数据挖掘问题的所有方法，如分类、回归、聚类、关联规则以及在新的交互式界面上的可视化。WEKA是开放源代码，新编写的算法只要符合其接口规范，就可以嵌入其中，从而扩充其原有算法。

以K-means算法为例，介绍在WEKA平台下如何聚类。WEKA平台把K-means算法的实现命名为“SimpleKMeans”算法，位于weka.clusterers.SimpleKMeans包中。以此构建聚类器，包括以下4个环节[8]：

(1) 读入样本数据；

(2) 初始化聚类器，采用setDistanceFunction(DistanceFunction df)函数计算距离；

(3) 使用聚类算法对样本进行聚类；

(4) 打印聚类结果。

3 算法性能分析实验

以K-means算法为例。实验中的数据来自于UCI数据集中的鸢尾花数据(Iris)，这是用于模式识别的数据集，常用来测试和比较数据挖掘算法。鸢尾花数据集定义了5个属性：sepal length、sepal width、petal length、petal width、class。其中，前4个属性均为数值型，单位cm；只有class为类属性。有 Iris Setosa、Iris Versicolour、Iris Virginica等3类，分别代表山鸢尾、变色鸢尾、维基亚鸢尾。每个类别都有50个实例，共有150条实例数据。使用WEKA平台中的现有算法SimpleKMeans、DBSCAN、EM、FarthestFirst对此数据集进行聚类测试，实验是在 Window 10 操作系统下进行的。

3.1 实验步骤

WEKA为用户提供了Explorer(探索者)、Experimenter(实验者)、Knowledge Flow(知识流)、Simple CLI(命令行)4种用户界面。我们使用Explorer图形用户界面对Iris数据集进行聚类分析实验。实验步骤如下：

(1) 在Preproccess选项卡中选open file按钮，导入Iris.arff数据集。

(2) 选择Explorer界面下的cluster选项卡，选择打开SimpleKMeans，设置参数。

displayStdDevs参数，用于是否显示数值属性标准差和分类属性个数。选择false，不显示。

distanceFunction参数，用来计算距离函数。使用WEKA默认的EuclideanDistance函数。

dontReplaceMissingValues参数，用来表示是否使用均值/众数替代缺失值。选择false。

maxIterations即最大迭代次数，设为500。

numClusters即聚类的簇数，设置为3，就是把150条实例聚成3类。

在preserveInstancesOrder下选择false，表示没有预先排列实例顺序。

Seed(种子数)，设置为10。

(3) 为了验证算法的正确率，实验采用监督模式(Classes to vlusters evalution)进行测试。监督属性为class。

(4) 点击start按钮，运行程序。

3.2 实验结果分析

SimpleKMeans算法的聚类分析结果如图1所示，监督模式的运行信息如图2所示，可视化簇分配如图3所示。错分实例为17个，占总数的11.3%。Cluster Instances信息栏，列出了各个簇中实例数目及百分比。Iris数据集的数据被预测成3个簇。其中，Cluster 0有61条实例，占实例总数的41%；Cluster 1有50条实例，占实例总数的33%；Cluster 2有39条实例，占实例总数的26%。采用监督模式进行验证，Cluster 0代表Iris Versicolour，Cluster 1代表Iris Setosa，Cluster 2代表Iris Virginica。该算法对Iris Setosa的预测分组与实际一致，对Iris Versicolour和Iris Virginica的预测分组与实际存在偏差，误差的平方和(SSE)为6.998。实验表明，该算法能够很好地对抽象的事物进行分组。Cluster centroids 列出了sepal width、sepal length、petal width、petal length等4个属性簇中心的位置。

图2 SimpleKMeans算法监督模式信息

图3 可视化簇分配

图3是以sepal width为横轴、以petal width为纵轴的可视化簇分配结果。其中，左侧为散点图，图中的符号×表示实例，□代表错误的聚类实例，颜色由实例的簇类别决定。从中可以看出，SimpleKMeans发现了3个簇：显示为蓝色的Iris Versicolour、显示为红色的Iris Setosa和显示为绿色的Iris Virginica。右侧的条状图显示了sepal width、sepal length、petal width、petal length属性值的随机分布情况，其中红色的X和Y分别表示当前以sepal width为横轴、以petal width为纵轴。条状图中，实例被放置在水平位置，所显示的颜色由所在簇类别决定，其中的点代表属性值的分布情况。

3.3 实验结果对比

评价聚类分析结果的优劣，最直观的方法就是看它与人工判断结果的吻合度。为了验证SimpleKMeans决策树算法的分类效果，分别采用DBSCAN、EM、FarthestFirst等3种聚类分析算法对Iris数据集进行了聚类实验。实验结果见表1。

表1 几种算法的聚类分析实验结果

从聚类形成簇的个数看，SimpleKMeans、EM和FarthestFirst算法都是形成3个簇，与人工判断一致。从误判率来看，SimpleKMeans算法的误判率最低，为11.3%。从建模的速度看，SimpleKMeans算法和FarthestFirst算法的运行时间最短，其次是DBSCAN算法，而用时最长的是EM算法。从迭代次数看，SimpleKMeans的迭代次数最少，且明显低于其他几种聚类算法的迭代次数。实验结果证明，对数值型属性采用SimpleKMeans算法得到的聚类效果比较好。

4 结 语

在WEKA中采用SimpleKMeans算法构建聚类器，并在WEKA平台上采用K-means算法对Iris数据集进行了聚类分析实验。结果显示，Iris数据集被预测成Cluster 0、Cluster 1、Cluster 2等3个簇，运行时间仅0.02 s，误判率只有11.3%。与DBSCAN、EM、FarthestFirst等聚类算法相比，K-means算法在误判率、运行时间、生成簇数、迭代次数等方面，与人工判断的吻合度最高。