米桑油田盐岩层定向钻井的井壁稳定性研究

吴 怡 卢运虎 刘书杰 王名春 洪国滨 吴晓冬

(1. 中海油研究总院有限责任公司， 北京 100028；2. 中国石油大学(北京)石油工程学院， 北京 102249)

伊拉克米桑油田钻遇地层层系众多，其定向井造斜点都位于复杂盐膏层处，曾有多个定向井段钻遇盐岩、膏岩及泥岩复杂互层。盐岩层大斜度定向钻井作业难度大，容易遭遇溢流、井漏、井塌、阻卡等钻井复杂情况，导致原井眼报废。针对米桑油田出现的盐岩蠕变缩径、软泥岩流动、泥页岩及石膏地层坍塌等现象，课题组以米桑油田盐岩层地质资料为基础，运用瞬时弹性分析法和有限元分析法，对盐岩层定向钻井的井壁稳定性问题进行了研究。

1 瞬时弹性分析法

采用瞬时弹性分析法研究井眼力学稳定性机理，基于如下4点假设[1]：(1) 地层是均匀各向同性、线弹性材料，井壁围岩处于平面应变状态；(2) 不考虑岩石与钻井液的物理化学作用所引起的力学性质的变化；(3) 不考虑温度应力的影响，忽略多孔弹性介质影响；(4) 井壁某一点的应力满足破坏准则时，井壁发生破坏。

1.1 井壁应力状态

针对井筒内压、地应力和压裂液渗流效应的联合作用，根据叠加原理，求得大位移井的井眼周围应力场分布。由于井壁上没有剪应力，其余2个主应力在井壁平面内，根据二维空间应力关系，得到三轴应力(σrr、σ1m、σ2m)的表达式如下。

(1)

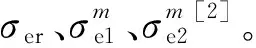
(2)

1.2 瞬时弹性坍塌压力

根据应力的莫尔圆关系，正应力和剪应力可以由最大主应力(σ1)和最小主应力(σ3)表示。通过三角运算，岩石平衡的极限应力状态可由式(3)表示。

(3)

当剪应力增大超出此状态时，岩石发生破坏，即井壁岩石不发生坍塌破坏的条件可表示为[3]：

(4)

1.3 瞬时弹性破裂压力

当井壁岩石所受有效拉伸应力达到岩石的抗拉强度时，岩石就发生破裂。对于拉伸破坏，一般采用最大拉应力理论，即当应力满足式(5)时，井壁岩石拉伸断裂。

σ3≤-|St|

(5)

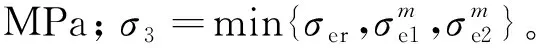
2 有限元分析法

为简化分析，假设：(1)盐岩地层为各向同性，且为平面应变问题；(2)静水压力不影响盐岩的蠕变；(3)广义蠕变速率(eij)与应力偏量(Sij)具有相同的主方向；(4)有效应力采用von Mises有效应力；(5)盐岩地层水平地应力为均匀的；(6)井内钻井液柱压力为pi，井眼半径为a，且井眼为垂直井眼。

2.1 蠕变稳定性模型

2.1.1 极坐标下的蠕变速率

将Heard蠕变本构关系表示的单轴应力下的表达式，转化成三轴应力下的表达式[4]：

(6)

其中，&ij为稳态蠕变速率，E为盐岩激活能，R为理想气体常数，t为时间(单位d)，θ为绝对温度，A、B为流变参数，μc为盐岩横向和纵向蠕应变速率的比值。由前面的假设可知，μc=0.5。

采用Von Mises有效应力，有：

(7)

根据式(6)(7)，可解得在极坐标下的蠕变率分量表达式[5]：

(8)

(9)

2.1.2 径向与周向应力差

径向应力与周向应力差的表达式如式(10)[6]。其中，N为非线性应力指数，N>1。

(10)

在蠕变前(t=0)的力学模型中，任取一点P为研究对象。设该点的极径为r0，则在任一时刻，该点的极径为r=r(t)=r0+uc，其中uc为该点的径向蠕变位移[7]，uc=uc(r0，t)。在假设的平面应变和轴对称应力边界条件下，任一时刻(t)的力学平衡方程和几何方程为：

(11)

(12)

双曲正弦函数为奇函数，得&r=-&θ，与式(12)联立求解，则

(13)

从式(13)可知，同一时刻，径向蠕变位移(uc)与蠕变前井距(r0)成反比。其中，c(t)为与时间有关的常数。将式(13)代入式(12)，可得

(14)

进而可得

(15)

将式(15)代入式(10)，可得径向应力与周向应力差的新表达式：

(16)

2.1.3 泥浆密度

由平衡方程式(11)，可得

(17)

根据力学平衡条件，有

(18)

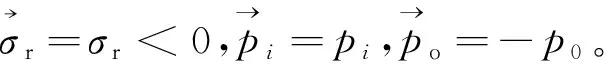
-(p0-pi)

(19)

由式(13)，取一井壁质点(井壁任一点)，由于该点在t=0时刻，极径r0=a0，于是可得：

c(t)=a0uc(a0,t)=a0[a(t)-a0)]

(20)

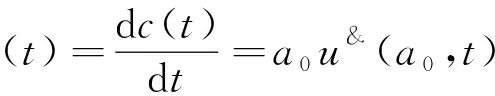
(21)

设n为某时刻t的井眼半径收缩速率，以百分数表示，n(t)>0，且

(22)

u&(a0,t)=-a0·n(t)

(23)

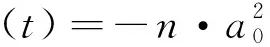
(24)

将式(24)代入式(16)，并化简，得：

(25)

设地下深度H处，钻井液密度为ρ，该处的井眼井壁内压(pi)为[8]：

pi=ρgH

(26)

将式(26)代入式(25)，计算可得：

(27)

式(27)即为控制井眼盐岩蠕变收缩的泥浆密度新的计算公式。由此，只要知道井眼起始半径(a0)即钻头半径，给定所需控制的井眼缩径率，当时的实际井眼半径(a)，就可求得维持给定井眼缩径率所需的安全钻井液密度下限值。

3 工程应用

3.1 X井的基本情况

米桑油田X井所钻遇地层上部以砂泥岩为主，中部以石膏、盐岩、页岩沉积为主，下部以碳酸盐岩地层为主。在盐膏岩夹杂页岩层位发现有高压溢流现象，并伴随缩径现象；在盐下碳酸盐地层易发生井漏和卡钻。通过对米桑油田已钻井复杂情况的统计分析，发现钻井中出现的工程问题主要表现是盐岩蠕变缩径、软泥岩流动、泥页岩及石膏地层坍塌和裂缝性灰岩地层漏失及坍塌。为提高整体的勘探开发经济效益，采用大斜度井钻井技术。大斜度井因为井斜角大、井眼长，又可能钻遇岩膏层，所以对井壁稳定技术提出了更高的要求。

3.2 岩石蠕变实验

对米桑油田X井盐岩岩心进行了三轴蠕变实验测试。实验岩心基本信息见表1，对应的多级应力加载曲线见图1和图2。

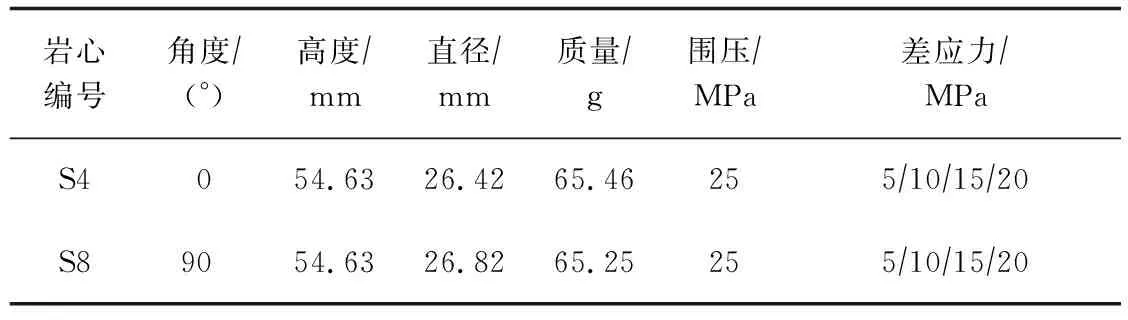
表1 实验岩心基本信息

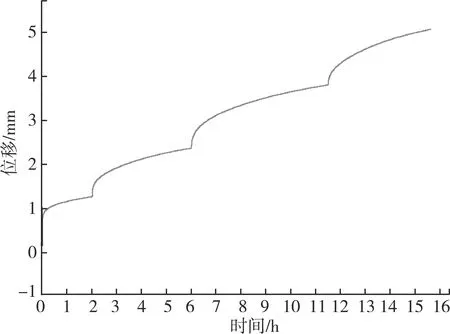
图1 盐岩S4的多级加载蠕变曲线

由图1和图2可知，在复杂盐膏层内的定向造斜井段，盐层稳态蠕变时间会受到井眼轨迹变化的干扰。盐岩S4达到4级加载曲线需要加载的时间为16 h，而在同等条件下盐岩S8需要加载40 h。S8沿晶面错动蠕变，需要更长的时间才能达到稳态蠕变。也就是说，当井眼逐渐向水平方向过渡时，更易达到稳态蠕变状态；同时，稳态蠕变速率的降低，会使得井眼的失稳风险降低。

S8盐岩需要较长的加载时间和较高的蠕变速率，说明垂直方向盐层内部的盐体晶面发育更为显著，导致差应力作用下盐体表现出较高水平的蠕变速率。因此，设计施工时应该考虑在复杂盐膏层段内的不同井斜处合理调控钻井液密度，从力学耦合的角度抑制钻进时盐层对定向井段整体的不对等蠕变，防止出现井眼尺寸波动过大，保持规整均匀。

3.3 瞬时弹性分析结果

根据上述计算模型，选取5°井斜角步长作为计算点，计算安全密度窗口，构建盐膏层内定向造斜井段的安全密度窗口。计算的安全密度窗口结果如图3所示。选取造斜点、复杂情况点等，计算坍塌压力、破裂压力，井周云图分布如图4所示。

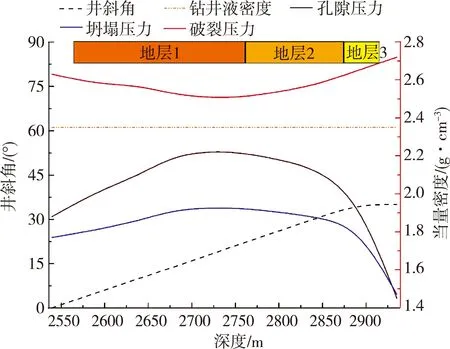
图3 X井盐膏层定向造斜井段安全密度窗口

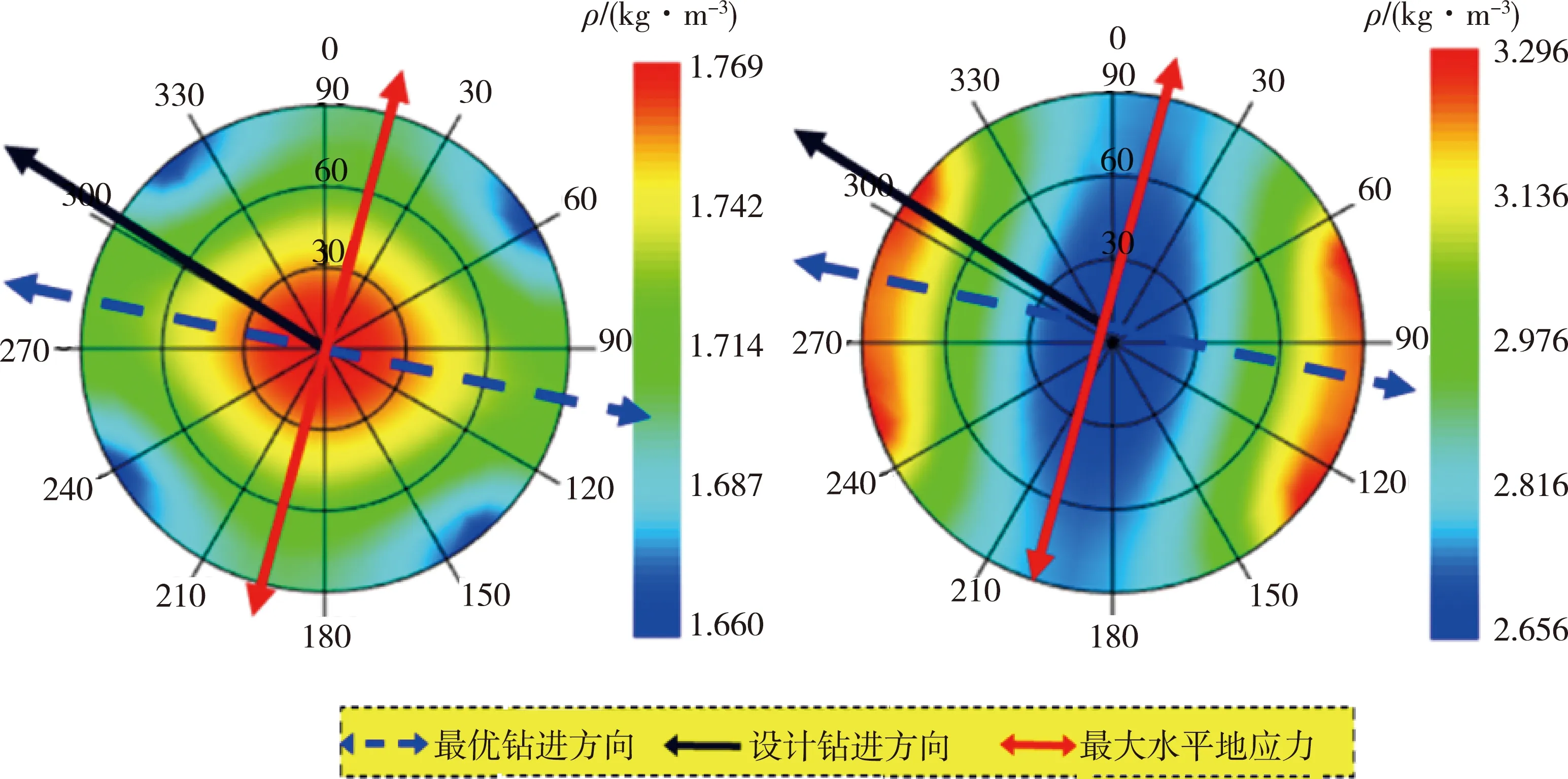
图4 X井造斜点坍塌、破裂压力云图

由计算结果可知，造斜点及复杂情况点的安全密度窗口较为宽裕，达0.75 g/cm3；而在深度2 800 m处，受到高压盐水层影响，缩小到0.34 g/cm3。由此可判断高压盐水层上部井段的瞬时弹性井壁稳定性能：从力学角度来看是较为稳定的，而从化学角度看，因受到复杂地层岩石岩性影响，钻井液流体与复杂盐膏层内不同岩性岩石的化学作用效果存在明显差异；下部高压盐水层井段的主要问题是安全密度窗口过于狭小，提高了对施工过程的压力控制要求。

3.4 有限元法分析结果

利用有限元软件(ABUQUS)分析了岩盐和泥岩的蠕变。采用深度2 725～2 734 m处的硬石膏-泥岩-岩盐-硬石膏组合的地层参数进行研究。其中，岩盐蠕变分析采用Heard模型，泥岩蠕变分析采用Weertman模型[9]。

数值模拟结果显示，地层岩石总体表现为轻微缩径。其中，泥岩缩径量相对较大，井眼打开大概11 d后，缩径量约为7.6 mm；盐岩缩径量较小，仅为0.8 mm左右。在钻井过程中，将表现为下钻遇阻、起钻遇卡、溢流和井漏等现象。生产实践中面临泥岩、岩盐和硬石膏夹层，可通过调节钻井液相关性能(如井下缩径频繁时可适当提高泥浆密度)来避免盐岩缩径、泥岩缩径及石膏的吸水膨胀和分散。

根据上述分析结果，在米桑油田X井成功实现盐岩层段造斜3°/30 m、井斜角35°的盐岩层定向钻井，钻井总工期比计划的97 d节约了30 d左右，井下无复杂情况。

4 结 论

(1) 根据岩石力学蠕变实验，石膏地层水平与垂直方向的力学参数相近，但整体强度高于盐岩；盐岩地层水平与垂直方向的力学性能差异明显，各向异性突出，弹性模量低，水平方向泊松比高。

(2) 从力学角度重点分析了X井盐膏层的坍塌压力和破裂压力，计算出盐膏层安全钻井液密度窗口为2.31～2.50 g/cm3。现场实践结果，有效解决了井壁稳定难题，保证了现场作业安全。

(3) 基于前人关于井壁稳定问题的相关研究成果及模型，联系米桑油田盐膏层地质实际，运用瞬时弹性分析法，描述盐岩层井壁应力状态，建立了瞬时弹性坍塌压力和破裂压力计算模型；应用有限元分析法，描述盐岩层定向井井壁蠕变稳定性，推导建立了新的泥浆密度计算公式。不过，提出的计算模型未考虑温度、应力、钻井液、多孔弹性介质等影响因素。