基于路程预瞄的驾驶员模型＊

2019-03-04杨浩黄江李攀韩中海

汽车技术 2019年2期

杨浩黄江李攀韩中海

（1.重庆工商职业学院，重庆 401520；2.重庆理工大学，汽车零部件先进制造技术教育部重点实验室，重庆400054）

主题词：路程预瞄路程预瞄曲率阈值预瞄距离可变模糊控制理论最优速度控制策略

1 前言

驾驶员行为规律及其建模在人-车-路闭环系统的仿真、评价与优化中具有至关重要的作用。研究人员根据预瞄理论提出了各种驾驶员模型：MacAdam提出了最优预瞄控制模型[1]，郭孔辉院士提出了单点预瞄最优曲率模型[2]，张慧豫提出了两点预瞄的新型驾驶员模型[3]，同时，汽车动力学仿真软件CarSim中采用了5点预瞄驾驶员模型。

近年来，随着控制理论的不断发展和完善，基于预瞄的各种驾驶员模型不断提出，主要有模糊控制驾驶员模型[4]、预瞄优化神经网络驾驶员模型[5]和自适应最优预瞄控制驾驶员模型[6]。上述方法在路径跟踪方面取得了一定进展，但并没有充分反映驾驶员的预瞄行为。郭孔辉院士的研究表明[2]，驾驶员预瞄更一般的形式是其目光不只集中于前方一点，而是着眼于前方的一段路，并争取使汽车在这一段路程内的运动误差最小，同时根据路程预瞄的有效信息和当前车速来调整预瞄距离，即预瞄距离应可变。因此，本文提出一种路程预瞄驾驶员模型，通过对路程预瞄，建立了预瞄距离随路程预瞄曲率阈值和车速可变的自适应跟踪模型。结合路程预瞄中点的修正和模糊控制理论，建立了智能控制转向盘决策模型。通过路程预瞄中点的理想侧向加速度、车辆实际侧向加速度、路程预瞄曲率阈值建立了最优速度控制策略。最后，结合智能控制转向盘决策模型和最优速度控制策略建立了基于路程预瞄的智能控制驾驶员模型。

2 基于路程预瞄的智能控制转向盘决策模型

2.1 路程预瞄模型的建立

驾驶员在路径跟踪的过程中对一段路程进行预瞄，本文建立了车辆坐标系下的路程预瞄模型，如图1所示。假设驾驶员跟踪的目标路径为f(x),在预瞄方向Xt上预瞄了一小段路程为(xt2-xt0)，对应的横向距离为(s2-s0)，对应的中点坐标为(xt1,s1)。

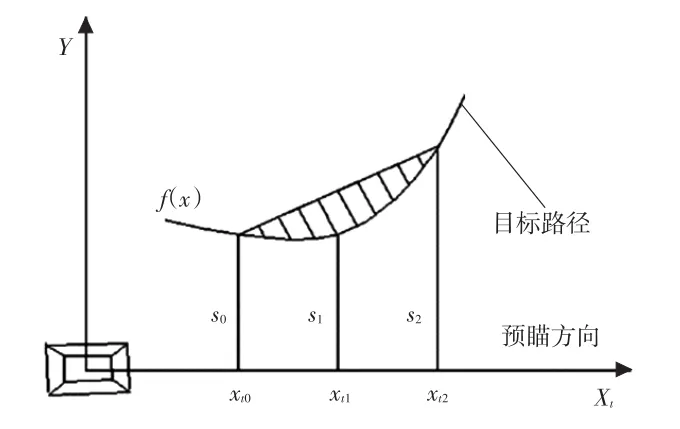
图1 路程预瞄模型示意

预瞄的路程为全局路径中的一段，只要保证该局部路径的跟踪精度，通过迭代即可实现全局路径的有效跟踪。只要保证局部路径的取值较小，用二次函数来描述基于(xt0,s0)、(xt1,s1)、(xt2,s2)3点的局部路径也可得到较高精度，简化了对复杂道路的拟合与求解过程。设预瞄视线内的一段道路方程为：

即驾驶员以N(xt)近似代替f(x)：

可以采用插值的方法求解N(xt)，常见的有Lagrange插值法和Newton插值法[7]。由于预瞄点的坐标变化时，采用Lagrange插值算法就必须重新计算插值函数的所有值，而采用Newton插值算法只需考虑更新的点，前2个点的值可以循环利用，计算速度更快，实用性强，同时对预瞄的前2个点的信息可多次利用，也体现了预瞄过程的连续性，即驾驶员在预瞄的过程中会结合前面预瞄点的有效信息来跟踪一段路。由此，可将预瞄视线内的一段道路方程表示成更为具体的Newton二次差值函数：

因此，在[xt0,xt2]上可以近似得到：

点(xt0,s0)、(xt1,s1)、(xt2,s2)是通过预瞄环节获取的，且均在f(x)上，所以有：

这样可以求得：

对f(x)在[xt0,xt2]内积分，结果即体现了这一段路程在预瞄方向的累计误差，同时计算出点(xt0,s0)、(xt2,s2)与Xt轴所围成的梯形面积，后者与前者的差值为：

由式（4）可得：

为简化计算，将式（11）转化为数值计算，可以采用Newton-Cotes积分或Simpson积分[7]，后者的精度比前者更高，故采用后者来计算式（11）中的积分：

进一步可得：

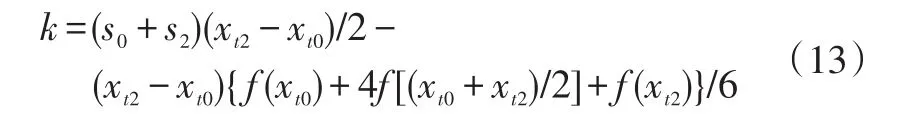
这样用数值计算代替了积分计算，减少了计算工作量，便于研究。因此，只需利用传感器探测出车辆前方预瞄方向上该段路程的预瞄距离|xt0xt2|及s0、s1和s2即可计算出k值，避免了对目标路径的拟合，方便应用于实车。k＞0表明目标路径是一条偏离预瞄方向的弯曲路径，k越大，f(x)在预瞄方向上的曲率越大；k=0表明目标路径是一条直线路径；k＜0表明目标路径是一条偏向预瞄方向的弯曲路径。因此，k在一定程度上表明了预瞄路程曲率的变化趋势，称其为路程预瞄曲率阈值。这样可以得到路程预瞄模型的结构框图，如图2所示。

图2 路程预瞄模型结构框图

2.2 预瞄距离可变的自适应跟踪模型

根据郭孔辉院士的“预瞄-跟随”理论[2]，在小曲率的道路上，驾驶员的最优转向盘转角为：

式中，i为转向系的传动比；L为车辆轴距；s为预瞄点的侧向误差；d=vT为预瞄点的距离；v为车速；T为预瞄时间。

式（14）中，i和L是车辆固有的参数，因而在路径跟踪的过程中保持不变，而预瞄距离应随路程预瞄曲率阈值和车速连续变化。

驾驶员跟踪的路径一般为直线路径与弯道路径的组合形式，因此假设驾驶员跟踪的目标路径f(x)分为直线路径、直弯过渡、弯道路径、弯直过渡、直线路径5个阶段，如图3所示，其中(x0,y(x))为车辆的初始位置。

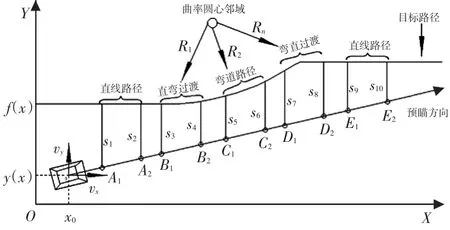
图3 预瞄距离可变的自适应跟踪示意

在直线路径阶段，假设驾驶员在视线前方预瞄了一段路程A1A2，其对应的侧向误差为s1、s2。随着预瞄距离的增大，预瞄点的侧向误差减小，即s2＜s1。由式（14）可知，δ2＜δ1。因此，驾驶员应优先选择终点预瞄，这样既可以减小预瞄点的侧向误差，又能决策出较小的转向盘转角，有利于提高车辆的操纵稳定性以及减轻驾驶员的转向负担。

在直弯过渡阶段，假设驾驶员在视线前方预瞄了一段路程B1B2，其对应的侧向误差为s3、s4。进入弯道时，侧向误差可能会随着预瞄距离的增大而增大，但由于预瞄终点的预瞄距离较预瞄始点的预瞄距离大很多，因而虽然预瞄终点的侧向误差可能有所增加，但是其增加量远小于预瞄终点与始点的距离之差，即|s4-s3|＜|B1B2|。由式（14）可知，其转向盘转角依然保持着随预瞄距离增大而减小的趋势，即δ4＜δ3。由于在弯道路径中，车辆所需的转向盘转角较大，所以始点预瞄优于终点预瞄。

在弯道路径阶段，目标路径并不是一个定半径的圆弧，每一点对应的曲率1/R1、1/R2…1/Rn并不完全相同，但每一点对应的圆的圆心可以组成一个曲率圆心领域。该领域所对应的曲率中总存在最大曲率1/Rmin和最小曲率1/Rmax。理论上，车辆在曲率最大处容易失稳，反之，不易失稳。但是研究人-车-路闭环系统，应考虑目标路径在运动车辆坐标系下时刻变化的因素，所以应当建立目标路径相对于车辆坐标系下的路程预瞄曲率阈值，驾驶员正是依据此阈值来决策路径跟踪的可变距离的。由前面的分析可知：随着预瞄距离增大，转向盘转角减小，即δ6＜δ5。由于弯道路径需要较大转向盘转角，故始点预瞄优于终点预瞄。在弯直过渡阶段，其原理与直弯过渡相反。

由以上对5个阶段的路径跟踪过程的分析可以得出：当路程预瞄曲率阈值较大时，预瞄距离应较远；反之，预瞄距离应较近。这体现了采用预瞄距离可变的自适应跟踪模型的合理性。由于真实驾驶员在高速工况下目光较远，低速工况下目光较近，因此有必要建立预瞄距离随路程预瞄曲率阈值和车速可变的自适应跟踪模型。参考生理、心理学家Land和Horwood对驾驶员在弯道行驶的行为研究表明[8-9]：驾驶员在驾驶车辆时视线集中的范围主要包括“远”（车前方10～20 m）、“近”（车前方6～8 m）2个区域。因此，本文给出预瞄距离d可变公式：

预瞄距离可变的自适应跟踪模型结构框图如图4所示。其中，车速v的范围为0～120 km/h，同时赋予初始预瞄距离为8 m。当v=120 km/h、k=0时，预瞄距离最远，为20 m。当车速一定时，预瞄距离随预瞄路程曲率阈值的增大而减小。当预瞄路程曲率阈值一定时，车速越大，预瞄距离越远。不同的驾驶员的k值和行驶的车速不同，选择的预瞄距离有所不同，但预瞄距离随路程预瞄曲率阈值的增大而减小，随车速的提高而增大的趋势是不变的。这也是有可能排除驾驶员的个性而建立统一的预瞄距离可变的自适应跟踪模型的依据。

图4 预瞄距离可变的自适应跟踪模型结构框图

2.3 基于路程预瞄中点的侧向误差及其变化率的修正

虽然驾驶员在路径跟踪过程中应尽可能使预瞄路程的累计误差最小，但驾驶员对一段路程的累计误差的感知程度比对单个点的感知程度更复杂（即注意力的分配问题）。进一步分析可知，如果路径跟踪过程中一段路程的累计误差最小，其预瞄路程上中点的误差也会比较小，如果能得知中点误差的变化率，就能预测下一时刻误差的变化趋势，从而预测车辆下一时刻是偏向还是偏离目标路径，这对车辆的路径跟踪有一定的预测作用。因此，把路程预瞄中点的侧向误差及其变化率作为修正量既能简化模型，也能提供预测，更有助于跟踪路径的实现。

预瞄路程中点的侧向误差可通过车身传感器直接获取，误差变化率的计算如图5所示，其中，ψ为车身纵轴与固定坐标系OX轴的夹角，ψd为道路中心线切线与固定坐标系OX的夹角，vx和vy分别为车辆质心的纵向速度和侧向速度。则车身纵轴与道路中心线切线的夹角为：

夹角ψ和ψd的变化率分别为：

式中，ρ为道路曲率；ωr为横摆角速度。

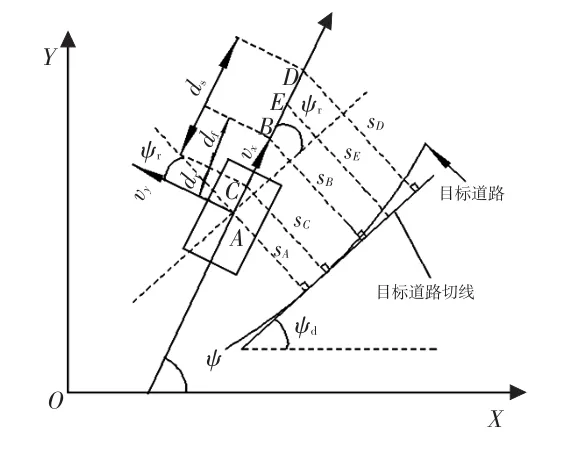
图5 侧向误差变化率计算示意

当目标路径曲率很小时，预瞄点到目标道路的距离近似等于其到目标道路切线的距离。设车辆的质心位置为A点，驾驶员在车辆中所处的位置为C点，B为路径跟踪的始点，D为路径跟踪的终点，E为BD的中点，dr、df、ds分别为其对应的预瞄距离，sA、sB、sD分别为其对应的侧向误差，质心与目标路径之间的侧向位置误差变化率为：

由于ψr非常小，故上式可简化为：

由图5的几何关系可得：

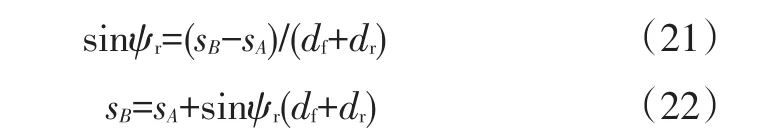
在夹角ψr非常小的情况下：

对sB求导可得：

将式（20）代入式（24）中，得到侧向误差变化率[10]的表达式为：

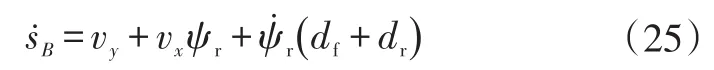
将式（18）代入式（25）中可得：

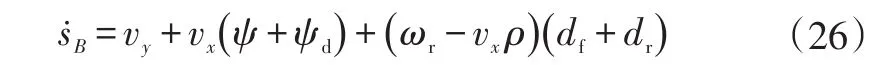
同理可得点E的横向误差变化率为：

这样，预瞄中点的侧向误差变化率已经建立，图6给出了中点修正的结构框图。

2.4 模糊控制理论

由于车辆的非线性因素不可避免，精确的人-车-路闭环系统模型很难建立。而模糊逻辑控制器能很好地适用于非线性系统，同时模糊逻辑驾驶员在一定程度上反映了人的思维和驾驶行为[11]。因此，将模糊控制器用于决策转向盘转角。图7给出了基于路程预瞄的模糊逻辑控制器结构。

图6 中点修正的结构框图

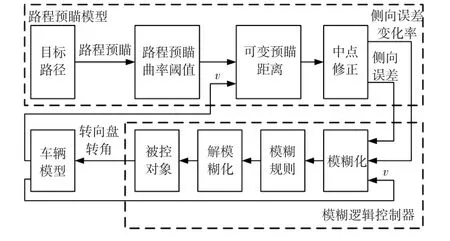
图7 基于路程预瞄的模糊逻辑控制器结构

其中，模糊化过程分两个部分。第一部分为将所选择的控制变量作为模糊控制器的语言变量。本文选择了3个输入变量，分别为侧向误差、误差变化率、车速。对侧向误差定义了7个语言变量，分别是负大（NB）为-5～-3 m、负中（NM）为-4～-2 m、负小（NS）为-3～0 m、正零（ZE）为-1～1 m、正小（PS）为0～3 m、正中（PM）为2～4 m、正大（PB）为3～5 m；对侧向误差变化率定义了3个语言变量，分别是负小（NS）为-8～-4 m、正零（ZE）为-4～4 m、正小（PS）为4～8 m；对车速v定义了4个语言变量，分别是负小（NS）为0～60 km/h表示低速行驶，正中（ZE）为50～70 km/h表示中低速行驶，正零（PZ）为60～90 km/h表示中速行驶，正大（PB）为80～120 km/h表示高速行驶。第二部分为定义模糊控制器输入和输出变量的论域，然后对整个论域进行模糊分割并给出相应的隶属度函数，隶属度函数选择三角函数。本文参考CarSim软件中道路的实际宽度为10 m，所以预瞄点到道路中心线的误差论域为±5 m；我国高速公路的最高车速为120 km/h，因此车速v的论域为0～120 km/h；转向盘转角δ的论域为-160°～160°，将此论域定义为-40°～40°，通过4倍增益来等效，便于论域整数划分。因此，可以得到84条模糊条件语句构成的控制规则表，如表1所示。图8所示为预瞄中点的侧向误差、侧向误差变化率、车速、转向盘转角的隶属度函数。

3 最优速度控制策略

由于真实的驾驶员会根据路程预瞄环节和感受的力反馈来调节车速，力的作用体现在加速度上，因此为了建立更逼真的驾驶员模型，本文基于路程预瞄环节和理想侧向加速度理论建立了最优速度控制策略。根据郭孔辉院士的“预瞄-跟随”理论[2]，预瞄点的理想侧向加速度为：

表1 转向盘控制规则

图8 隶属度函数

这样结合路程预瞄环节、理想侧向加速度理论、模糊逻辑控制器，可以建立最优速度控制策略框图，如图9所示。

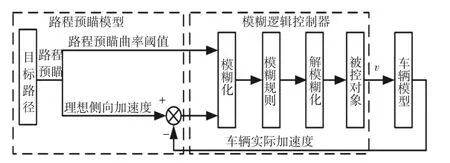
图9 最优速度控制策略框图

定义(ÿ*-a)的论域为-4～4 m/s2，分别用负大（NB）、负小（NS）、正中（ZM）、正小（PS）、正大（PB）来表示理想加速度与实际加速度的趋近程度。路程预瞄曲率阈值的论域为-4～4 m2，用负小（NS）表示偏向的大曲率路径，正零（ZE）表示直线路径，用正小（PS）表示偏离的大曲率路径。模糊逻辑控制器的输出为最优控制速度，其论域的定义与前文同理。这样通过模糊控制理论对加速度差值和路程预瞄曲率阈值进行模糊推理来决策最优控制速度，实现车辆的合理加、减速。当理想加速度与实际加速度的差值为负且曲率较大时，车辆减速，反之加速。其具体模糊规则如表2所示，图10给出了(ÿ*-a)、k、v*的隶属度函数。

表2 车速控制规则

图10 隶属度函数

4 基于路程预瞄的智能控制驾驶员模型

结合路程预瞄转向盘决策模型和最优速度控制策略，给出基于路程预瞄的智能控制驾驶员模型结构框图，如图11所示。

图11 基于路程预瞄的智能控制驾驶员模型结构框图

5 仿真验证

为了测试本文提出的驾驶员模型路径跟踪的有效性，基于CarSim与MATLAB/Simulink构建的联合仿真平台进行仿真验证。

该仿真平台由CarSim提供车辆动力学模块，即CarSim-S函数。在Simulink中搭建算法和智能控制方法，主要包括路程预瞄曲率阈值计算系统、预瞄初值赋予系统、预瞄距离可变系统、理想侧向加速度系统和2个模糊逻辑控制器。仿真平台系统结构如图12所示。

图12 仿真系统结构

为有效检验本文所设计的驾驶员模型的跟踪精度和适应性，跟踪路径分别选择双移线路径和复杂路径。双移线路径可视为对超车动作的仿真，也包括驾驶员特性在内的“闭环验证”，在一定程度上表现出汽车转向运动的综合能力。复杂路径包括10个半径不同的弯角，主要用于验证在不同曲率路径上车辆的跟踪效果。为验证最优速度控制策略的合理性，分别进行初始速度为120 km/h的双移线路径验证和初始速度为60 km/h的复杂路径验证。仿真结果如图13所示。

图13 仿真结果

将路程预瞄驾驶员模型与CarSim驾驶员模型进行对比。从图13可以看出：在双移线路径中，前者能更好地逼近预期路径，并可在驶入弯道时提前减速，弯道内低速匀速行驶，后者没有实现合理的加、减速控制；在复杂路径中，两者与目标路径趋于重合，前者路径跟踪精度高，在直线路径阶段，目标车速实现了提前减速，在弯道路径阶段，目标车速已降速并匀速驶入弯道，即弯道低速匀速行驶，后者以恒定的目标车速跟踪整个路径，即没有实现合理的加、减速控制。以上仿真结果表明：该驾驶员模型能够适应从低速到高速不同曲率的路径跟踪，具有跟踪精度高、速度调节合理、适应性强的特征。