结合模糊理论的田口算法预测钻孔参数研究

2019-03-01钱程车英李瑞

长春理工大学学报（自然科学版） 2019年1期

钱程，车英，李瑞

（1.长春理工大学光电工程学院，长春 130022；2.长春理工大学经济管理学院，长春 130022）

钻孔作业作为金属材料成型工艺之一，是机械制造的重要组成部分[1]。在钻孔切削过程中，进给速度、钻头钻速和钻头直径这些组合参数的搭配使用会影响到钻孔过程中的钻头振动，振动会导致钻孔质量下降，如：孔位水平偏差、尺寸过大、孔位轴线偏移、孔相对位置偏差等，严重时会导致钻头断裂。许多研究人员试图通过各种方法加工材料来克服钻孔过程中的困难[2-3]。

对于钻孔质量的影响因素，多数方案均采用了各种基于计算机的软件技术，如田口法和响应曲面法等来优化工艺参数。Palanikumar等人进行了使用HSS麻花钻头的试验，并使用方差分析（ANOVA）和回归分析了输入和输出特性[4]。Davim等人采用田口的技术来优化CFRP复合材料的加工参数[5]。而对于多个响应因素需要同时分析的情况，灰色关联模型是一种有效的分析方案。Palanikumar等人研究了输入加工参数（如钻头直径，主轴转速和进给速率）的影响，并使用灰色关联等级方法针对表面粗糙度和推力等多种响应进行了优化[6]。

模糊理论是通过构建一个基于模糊逻辑规则在输入和输出变量之间建立关系的模型。其拥有结构简单、逻辑易修改等优点，已广泛应用于各领域。灰色关联模型便是一种模糊逻辑技术。

Taguchi正交方法是一种应用于少量数据进行分析预测的数理统计方法[7]。利用正交表将试验次数大幅度缩减，选出几组代表性强的数据进行合理试验后，对结果比较分析，得出最佳试验方案的方法[8]。

文中使用Taguchi的L25正交阵列进行实验。输入钻孔直径，进给速率和主轴转速等工艺参数。采用灰色关联技术分析钻孔过程中的推力，振动等多个特征参数。通过方差分析法可以分析影响钻孔过程中最重要的因素。并构建一个数学模型，用模糊逻辑来预测输出响应，并将其转化为工程使用模型，提出具有更高准确度的钻孔作业方案。

图1 研究方法流程图

如图1所示，文中提出研究方案整体步骤，现构建钻孔实验设备，通过实验证明方法可行，同时提出参数优化方案。

1 实验设备与原理

本文钻孔设备由三相异步交流电机、两相步进电机、旋转传动结构、进给传动结构、控制箱、控制屏、底座（内含控制柜）等几部分组成。其力学传递模型如图2所示。

图2中，压力传动过程为：钻孔作业时钻头7接触待加工工件受压，上部齿条将压力传导至齿轮6，再经过主传动轴5传递，经由蜗轮4带动蜗杆3向上，利用杠杆原理，在步进电机2下方适当位置处设置压力传感器1，实时接收挤压压力并将压力数据传回PLC记录，为后续分析做准备。

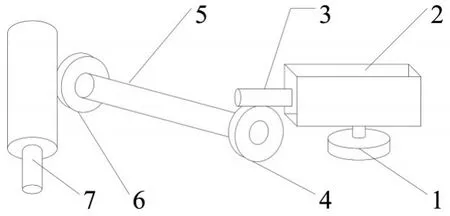
图2 力学传递模型示意图

在主传动轴5一侧装有螺旋弹簧，防止空回；驱动单元采用蜗轮蜗杆传动，使机构更紧凑，传动更平稳，承载能力增大。将压力传感器安置在后端位置无需考虑在钻头正上方提供探测点，探测结构简单，可有效节省空间；通过探测经动力传递结构传回的受力信息，内含结构振动反馈，闭环控制效果更为真实有效。结合力学传递模型，假设探测点与钻头压力均为竖直方向，同时假设主传动轴受力均匀，无力矩损失，忽略运动过程中摩擦损耗对压力传递模型的影响，则对于钻头、压力传感器、支点存在力矩相等关系，即：

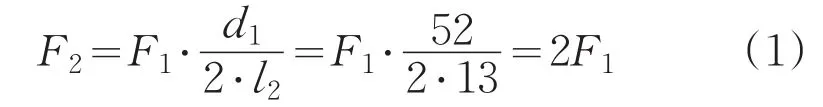
式中，F1为钻头受到压力，d1为齿轮6分度圆直径，F2为压力传感器处受到压力，l2为压力传感器距支点垂直距离。结合现有结构设计合理力臂，对传感器处压力值放大2倍，结合实际值选用深圳力信AS-W10压力传感器，表1是其主要技术指标。

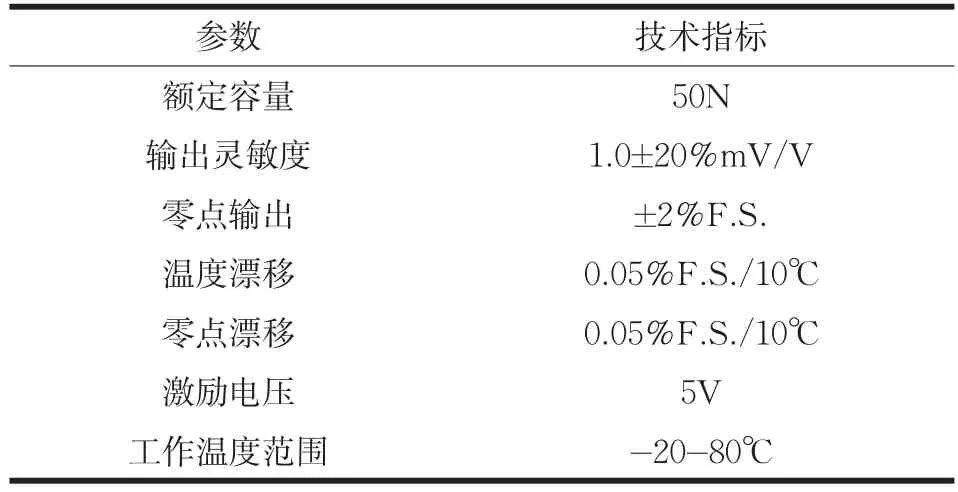
表1 AS-W10传感器参数表

2 钻孔实验

钻孔实验由上述设计的垂直钻孔设备和压力传感器结合完成，用于测量钻孔作业期间产生的切削力和振动变化，用压力传感器传回数据的期望值表示切削力；对测试数据分5段，用各段切削力值最大值与最小值的差值的期望表示作业振动。使用的实验装置如图3所示。实验用钻头为HSS高速钢钻头（直径：3.2mm 3.5mm 4mm 4.5mm 4.8mm），钻孔作业材料为2A12铝合金，参数见表2。

图3 钻孔设备实物图

表2 2A12铝机械物理性能表

在本次实验中，对输入参数（进给速率、钻头直径、主轴转速）在不同范围内进行了详细的测试。使用Taguchi正交化实验方法对表3数据进行处理，矩阵的统计结果处理使用Minitab17软件完成结果分析。Taguchi方法是通过对自变量的归一化处理，得出各个影响因子对实验结果的作用的数理统计方法，对于整体分析因为运用该方法使得实验数量有效缩短。具体实验数据如表4所示。

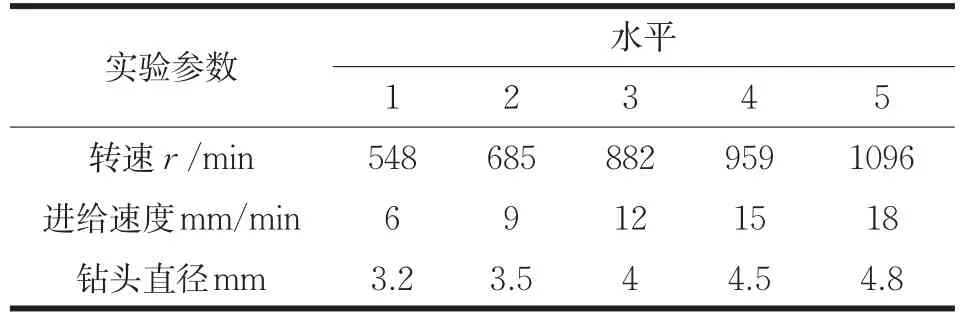
表3 田口水平表

分析钻头转速、进给速度、钻头直径对钻孔作业中的推力和振动的影响。对于钻孔作业，作业过程中的推力和振动越小，相应的作业精度也就越高。对应于Taguchi方法，应使用望小特性对整个实验数据进行分析，无论使用哪种特性，信噪比越大越好。

望小特性信噪比定义为：

式中，η为信噪比，μ2为测试变量期望值的平方，在Taguchi方法中称之为灵敏度，σ2为测试变量方差。

望小特性信噪比估计值为：

式中，n为试验次数，yi为测试指标输入值。

信噪比估计值的分贝为：

表4 田口方法正交实验表

利用表4中的实验数据，通过建立基于Taguchi方法L25正交表分析实验结果。对处理后得出的信噪比直接观测，得出最优加工作业方案，提升加工精度。

3 Taguchi实验结论

表5为实验过程推力与振动的信噪比响应结果。在望小特性分析中，信噪比结果越大越好。Δ表示各水平间极差值，极差值越大，对指标影响越显著。运用直观分析方案对实验结果进行说明，为追求信噪比最大，Taguchi方法认为，最优方案是转速采用水平5，进给速度采用水平1，钻头直径采用水平1。

表5 信噪比响应表

从表5可知，对于推力响应，影响最大的是进给速度因子；而对于振动响应，影响最大的是钻头直径因子。

前文Taguchi方法只确定了各因子对于某个响应的影响程度，无法将两个响应结果结合分析与优化作业参数。为此，文中选用灰色关联模型理论分析实验中不同响应之间的关系，对测试结果进一步优化，寻求最优方案。

4 灰色模型分析与结论

灰色理论多分析多变量响应问题。黑色代表无有效数据，白色代表数据对研究变量存在定量关系[9]。灰色模型可测量序列之间最近的相关性，明确各变量之间的关系。

使用表5所示的田口正交阵列和改进灰色关联分析来研究多重响应特征。

图4 灰色分析流程图

按照图4步骤进行灰色关联分析。首先标准化处理实验数据，使用“成本型”标准化处理方案将推力值和扭矩值转化为[0，1]区间内的数，标准化公式如下：

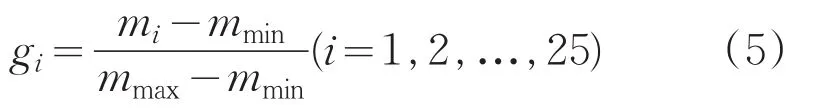
式中，mi为第i次实验测试值，mmin为实验最小值，mmax为实验最大值。

基于标准化结果，确定偏差序列：

从前文工作可知，比较序列为推力值与振动幅值，而文中的参考序列并不单纯是时间序列，在此提出一种基于实验数据的参考序列模型函数表示作业优化程度，用于后端灰色分析。

钻孔作业中，为追求更高精度，需提供更小的推力与振动，并考虑作业效率，为推力和振动的实验结果添加响应权重再综合，得出参考序列。参考序列公式为：

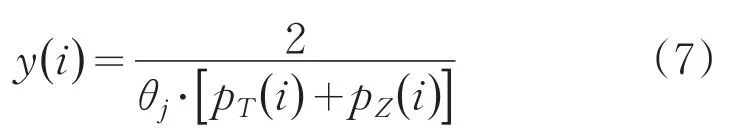
式中，y(i)为参考序列值，pT为推力偏差序列值，pZ为振动偏差序列值，θj为效率因子，由作业时间决定。表6为数据标准化结果。

表6 数据标准化表

运用表6结果，进行灰色关联分析。确定灰色关联系数，公式为：

式中：ρ为分辨系数，在区间[0，1]上选取，文中使用0.5进行灰色预测。

确认灰色关联系数，得灰色关联度：

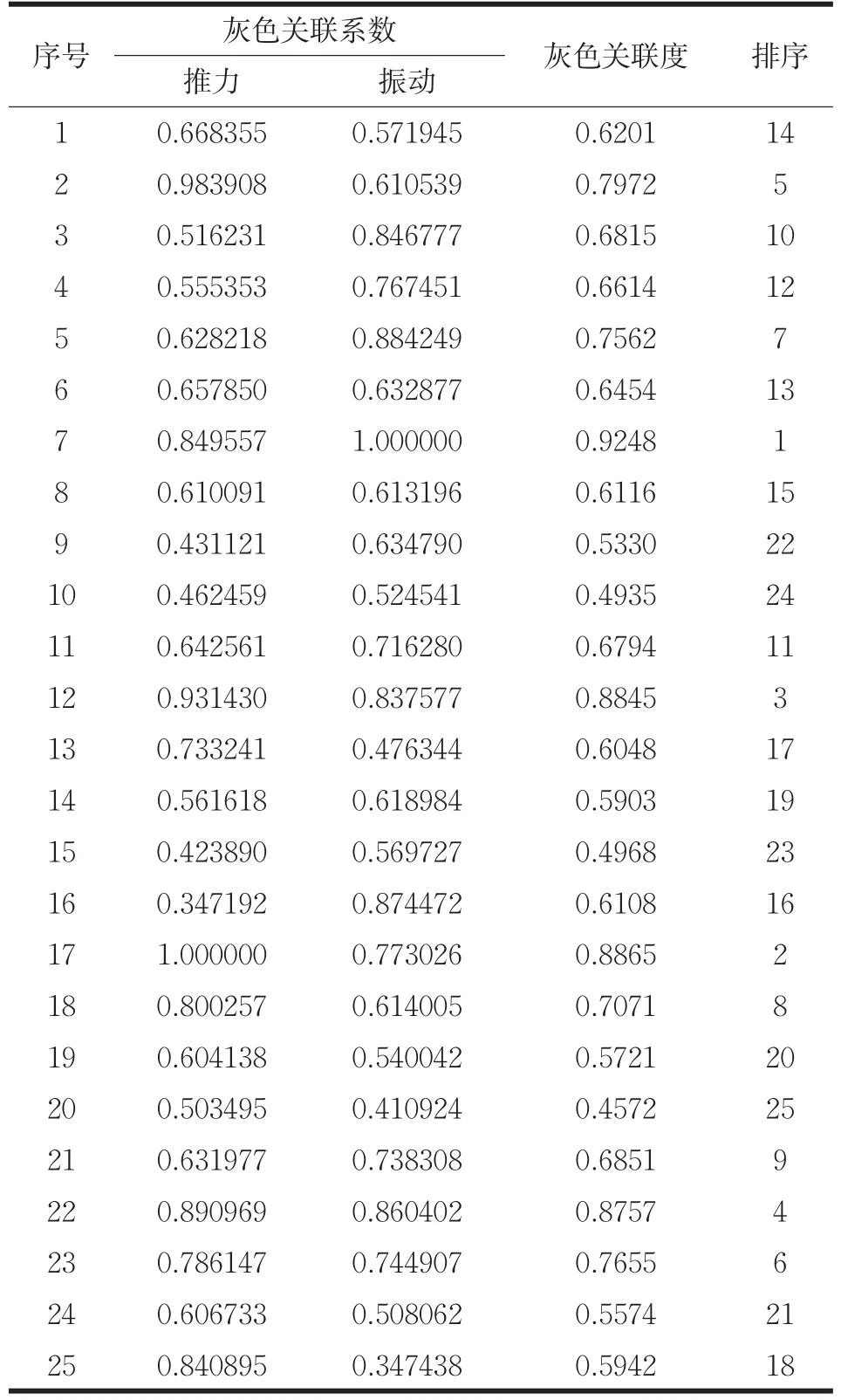
表7 灰色关联系数与灰色关联度

在过去的几十年中，大多研究人员只进行单一响应特性分析。本文使用灰关联模型可实现多个给定输入参数性能特征的同时测量。

从表7可以看出，实验7的灰色关联度值最大，为0.9248。实验7对应的主轴转速，进给速度和钻头直径分别是685r/min，9mm/min和4mm，且实验7数据是上述的25组钻孔参数中能够同时实现多个性能（推力、振动和作业效率）的最佳钻孔参数。

同时利用灰色关联度分析中的参考序列模型，使用Taguchi方法进一步分析，预测出最佳加工参数。

表8 参考列信噪比响应表

从表8可以看出，对于整体参考序列而言，使用Taguchi方法预测最佳结果为转速采用水平3，进给速度采用水平4，钻头直径采用水平1；对于整体参考序列的响应，影响最大的是钻头直径，其次是进给速度，再次是钻速。

由于直观分析无法表明各因子对于参考值响应的影响程度，对表7预测数据进行方差分析，使用F检验法，确定各因子与响应影响结果的差异，设实验中的F值为Fx，一般条件下：

Fx＞F0.1（n1，n2）时，则该因子对实验响应有影响；

Fx＞F0.05（n1，n2）时，则该因子对实验响应有显著影响；

Fx＞F0.01（n1，n2）时，则该因子对实验响应有高显著影响。

表9 参考列方差分析表

临界值Fα：F0.01（4，12）=5.412，F0.05（4，12）=3.259，F0.1（4，12）=2.48

从表9可以看出，各个因子对参考列的影响排序为：钻头直径＞进给速度＞转速，其中钻头直径影响为高显著，百分比为55%；其次是进给速度的影响，也对响应有显著影响，占22%；再次是转速，同样对响应存在显著影响，占17%，分析误差为5%。方差分析结论与田口分析相同，确定相应参数优化顺序为钻头直径，进给速度，转速。

5 模型预测结论

使用Taguchi方法建立田口L25正交表进行实验，对钻孔作业过程中的推力与振动进行数据分析，并采用灰色关联分析得出在实验数据中最佳钻孔参数，结合加工效率再次利用参考序列使用Taguchi方法分析，预测最佳方案，结论如下：推力响应影响程度从大到小为：进给速度，转速，钻头直径；振动响应影响程度从大到小为：钻头直径，进给速度，转速；结合加工效率的综合响应，影响程度从大到小为：钻头直径，进给速度，转速。