合取型集值序信息系统组合熵和组合粒度研究∗
2019-03-01王青海
李 燃 王青海
(青海师范大学计算机学院 西宁 810000)
1 引言
1982年,波兰数学家Pawlak提出了粗糙集理论,它是一种在实际应用中能解决数据属性约简和规则挖掘问题的数学工具[1~2],其应用核心基础是从近似空间导出一对近似算子,即上近似集和下近似集[3],并在很多方面都有成功的应用[4~5]。但由于经典粗糙集是基于论域上的等价关系,而现实世界的实际问题中等价关系并不多见,为此很多学者对其进行了扩展研究[6~7]。
在现实问题中,人们常会遇到诸如区域经济分析、市场占有率、从业行业分析等属性具有偏好关系的一类信息系统,这类信息系统往往是不完备的信息系统,即某些属性的取值是不确定的,可能是一个集合里面的不同值[8]。张文修、梁怡等把这样的不完备的信息系统称为集值信息系统[9],在不完备信息系统中,分别提出了乐观与悲观两种形式的多代价决策粗糙集方法[10]。文献[11]讨论了在集值信息系统中属性值为区间的集值信息系统,将区间集值信息系统分为析取型和合取型集值信息系统,而且建立了两者的优势关系,基于优势关系在粗糙集上进行了研究。文献[12]在合取型和析取型集值信息系统的基础上,针对两种集值序信息系统对决策规则和属性约简进行了研究。文献[13]提出一种特殊的属性偏好关系,这种偏好关系能够解决一类属性偏好既不是递增有序也不是递减有序,而是属性值趋向于标准属性值的问题,称之为属性集中有序。
信息系统的不确定性度量是从信息视角研究其信息结构的一种重要度量,包括从信息熵、粗糙熵、信息粒度、知识粒度等角度进行阐明。根据经典粗糙集近似空间中粒度的大小关系,不同信息系统中的关系有不同粗细程度,很多学者采用上述度量对信息系统进行了不确定性研究。文献[14]通过粒计算中知识的不确定性问题,分析了粗糙集、模糊集以及熵空间等理论模型,对各种理论模型进行讨论,对知识粒度进行了统一的描述,提出了知识不确定性与变化的知识粒度之间的联系。文献[15]中对信息系统分类能力的双论域粗糙集的不确定性进行研究,主要包括粗糙集的信息熵和信息粒度的定义及推广。文献[16]基于相容关系的粗糙集模型,提出了覆盖的组合熵和组合粒度的概念,研究了他们之间的性质与规律。文献[17]针对粗糙集理论中不完备信息系统,提出了一种知识粒度的定义,并研究了知识粒度与信息熵的关系,为知识的度量和知识的评价提供了一种可行的方法。文献[18]针对析取型集值序信息系统优势关系过于宽松的情况,引入了优势程度的参数问题,对信息熵和知识粒度不确定性进行了讨论。而组合熵与组合粒度是度量信息系统不确定性的有效方法,其优点在于具有对信息增益的易理解性。本文对合取型集值序信息系统采用组合熵和组合粒度进行不确定性度量研究。
2 基础部分
2.1 集值序信息系统
定义1[9](信息系统)设一个信息系统 S=(U,AT ,V,f),其中U={x1,x2…,xn}是一个非空有限的对象集,每个xi(i≤n)为其中一个对象,AT={a1,a2…,am}是信息系统里非空有限的属性集,每个aj(j≤m)为其中一个属性,V是信息系统属性值的集合,f是U×AT到V的幂集P(V)的一个映射,即对∀x∈U,a∈AT,f(x,a)∈P(V)。
根据集值信息系统的定义,把集值信息系统中元素之间是合取关系或析取关系的集值信息系统称为合取型集值信息系统或析取型集值信息系统。若在集值信息系统某些属性值上建立优势关系,则把属性归为一种准则,把集值信息系统称为集值序信息系统,将合取型集值信息系统或析取型集值信息系统称为合取型集值序信息系统或析取型集值序值信息系统。本文仅介绍合取型集值序信息系统。
2.2 合取型集值序信息系统
例1 表1为一个合取型集值序信息系统,表示为学生学习能力的统计信息,其中U={x1,x2,x3,x4,x5,x6}表示6个不同的学生,AT={a1,a2,a3,a4}={理论能力,实践能力,应用能力,创新能力},V={a,b,c,d}={C语言,数据库设计,计算机网络应用,数据结构}。

表1 一个合取型集值序信息系统
如表中x1(a2)=表示学生x1至少掌握数据库设计,至多同时掌握数据库设计和数据结构,在合取型集值序信息系统中,集合元素之间的关系是合取关系,也即“且”关系,针对合取型集值序信息系统,定义如下优势关系。
定义2[12](优势关系)设一个合取型集值序信息系统S=(U,AT,V,f),∀A⊆AT ,定义的优势关系为={(x,y)∈U×U|||≥ ||˄ ||≥ |},其中a∈A,||⋅代表集合的基数。
下限集合表示一名学生至少掌握的专业课,上限集合表示一名学生可能掌握的专业课,没有定义各门专业课的重要程度,用掌握的专业课门数即基数来定义优势,这个优势关系可理解为在属性集合A中,x优于y当且仅当x下限中元素的基数大于或者等于y下限中元素的基数,同时满足x上限中元素的基数大于或者等于y上限中元素的基数。例上表x=a3(x3)=y=a3(x4)=,为了表示方便,V的下限用表示,V的上限用表示,由于此时=,>,所以在应用能力方面,学生x3优于学生x4。根据定义1,容易得出如下定理:
定理1 设一个合取型集值序信息系统S=(U,AT,V,f),∀A⊆AT ,可得:
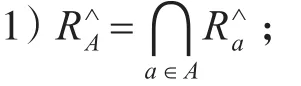
证明 1)
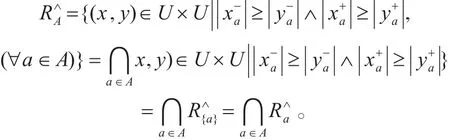
定义3(优势类)设一个合取型集值序信息系统S=(U,AT,V,f),∀A⊆AT ,设满足属性 a(a∈A)下优势关系优势类的集合表示为[={y∈U|(y,x)∈,论域U上所有优势类的集合表示为{[x∈U}。
定理2 设一个合取型集值序信息系统S=(U,AT,V,f),∀M,N⊆AT ,可得:
3)若 xi∈[xj],则 [xi]⊆[xj],其 中 [xj]= ∪{[xi]|xi∈[xj]} 。
同理可证2)成立。
3)若存在 xi∈[xji,j∈{1,2,…n},根据优势关 系 的 定 义 有 ∀a∈A, 即 (xi,xj)∈则||≥ ||˄ ||≥ ||, f(xj,a)⊆f(xi,a)同 理∀x∈[xif(xi,a)⊆f(x ,a ) ,所 以 f(xj,a)⊆f(x ,a ) ,有 x∈[,由定义3和定理2可得x∈[x],[x⊆[x,其中 [x=∪{[x|x∈[x},ijijjiij f(xi,a)∈p(v),f(xj,a )∈p(v)。
定义4(粒度粗细)设一个合取型集值序信息系 统 S=(U,AT,V,f),∀M∈AT,∃N∈AT,使 得[x]⊆[x],则称满足优势关系优势类的集合U/细于U/R,即M比N精细,记作M≺N 。
例2 根据表1所给出的合取型集值序信息系统,U={x1,x2,x3,x4,x5,x6},AT={a1,a2,a3,a4},设N={a1,a2},M={a1,a2,a3},各个优势类的集合为[x1]={x1,x3,x4,x6},[x2]={x1,x2,x3,x4,x6},[x3]={x3,x6},[x4]={x1,x3,x4,x6},[x5]={x1,x3,x4,x5,x6},[x6]={x3,x6},[x1]={x1,x3,x6},[x2]={x1,x2,x3,x6},[x3]={x3,x6},[x4]={x1,x3,x4,x6},[x5]={x3,x5,x6},[x6]={x3,x6}, 可得 [x]⊆[x],M ≺ N 。
定理3 设一个合取型集值序信息系统S=(U,AT,V,f),若 M≺N ,即 [x]⊆[x],则 | [x]|≤|[x],其中 |. |代表集合的基数。
证明 由定理2可得。
3 组合熵和组合粒度
3.1 知识的组合熵
定义5(组合熵)设一个合取型集值序信息系统S=(U,AT,V,f),∀A⊆AT定义知识A的组合熵为则0≤CE(A)<1。约定:当={[x]|x∈U}时,即优势关系的集合为单元素集,|=0,此时组合熵CE(A)取最大值1。由上述定义是优势关系上优势类的集合,|[ xi|表示在合取型集值序信息系统中优势关系优势类集合的基数。
定理4 设一个合取型集值序信息系统S=(U,AT,V,f),若 M,N⊆AT ,M≺N ,则CE(M)≥ CE(N)。
证明 若 M≺N,由定义知,∀xi∈U,使得[xi]⊆[xi], 即 ||[xi≤ ||[xi],于是CE(M)=)=CE(N),所以有 M≺N ,存在CE(M)≥CE(N)。
由定理4得出,当优势关系的集合越细时,组合熵的值也越大,集合越粗时,组合熵的值越小。组合熵反映了优势关系的分类能力,当组合熵的值越大,表示知识的不确定性越弱,区分能力越强。
例3 根据例2可得CE(N)=28/45,CE(M)=7/9,CE(M)≥CE(N),结果与定理4一致。
3.2 组合粒度
定义6(组合粒度)设一个合取型集值序信息系统S=(U,AT,V,f),∀A⊆AT ,定义知识A的组合粒度为,则有 0<CG(A)≤1。约定:当U/={[x]|x∈U}时,即优势关系集合为单元素集,|=0,组合粒度CG(A)取最小值0。
定理5 设一个合取型集值序信息系统S=(U,AT,V,f),若 M,N⊆AT ,M≺N ,则CG(M)≤ CG(N)。
证明 若 M≺N ,由 ∀xi∈U ,使得 [xi]⊆[xi],则 ||[xi]≤ ||[xi],于是 CG(M)=)=CG(N),所以有 M≺N,存在CG(M)≤ CG(N)。
例4 根据例2可得:CG(N)=17/45,CE(M)=2/9,CG(M)≤CG(N),结果与定理5一致。
结合定理4和5可以得出,当优势关系下的集合越细时,组合熵的值也越大,相反组合粒度值越小;集合越粗时,组合熵的值越小,组合粒度的值反而越大。那么组合熵组合熵和组合粒度之间是否存在某种关系,下面进行讨论。
3.3 知识的组合熵和组合粒度之间的关系
定理6 设一个合取型集值序信息系统S=(U,AT,V,f),∀A⊆AT ,知识A的组合熵和组合粒度有如下关系:CE(A)+CG(A)=1。
证明
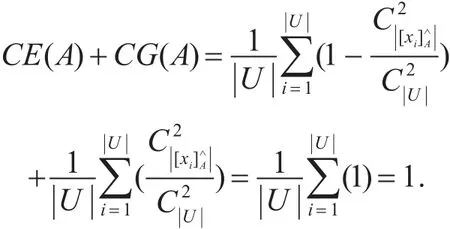
例5 根据例3与例4的结果可得CE(N)+CG(N)=1,CE(M)+CG(M)=7/9+2/9=1,满足定理6。
4 优势关系的优化
前面在定义优势关系时,比较x与y上下限中集合基数的大小,例如表1中x1(a2)与x4(a2)上下限的基数的大小相等,所以x1(a2)优于x4(a2),同时x4(a2)也优于x1(a2),在实际问题中并没有考虑其它因素来定义优势关系,例各门专业课重要程度和选修的时间等。现引入权值wi表示未考虑因素的重要程度,例定义C语言,数据库设计,计算机网络应用,数据结构的权值分别为3,4,5,6。定义如下优势关系:
定义7(优化后的优势关系)设一个合取型集值序信息系统S=(U,AT,V,f),∀A⊆AT,a∈A,定义优势关系为={(x,y)∈表示xi在属性a的下限或上限权值的求和。
注意,定义7满足定义2且上下限相等才存在的优势关系,那么这个优势关系可以理解为在属性集合A中,当x和y上下限集合基数相等,若满足x下限中所有元素权值的求和大于或等于y下限中所有元素权值的求和,且x上限中所有元素权值的求和大于或等于y上限中所有元素权值的求和,则定义x优于y。例如表1中 x1(a2)=x4(a2)=,得出 x1(a2)与 x4(a2)上下限的基数相等,权值=11,满足,可得在实践能力方面,学生x4优于学生x1。
定理7 设一个合取型集值序信息系统S=(U,AT,V,f),∀A⊆AT,∀a⊆A,是上优势关系相等的部分,可得:

证明 略
定义8(优化后的优势类)设一个合取型集值序信息系统S=(U,AT,V,f),∀A⊆AT,∀a⊆A,满足属性a下优化后优势关系的优势类表示为={y∈U|(y,x)∈,U上所有优势类的集合表示为{[x]|x∈U}。
定理8 设一个合取型集值序信息系统S=(U,AT,V,f),∀I,J⊆AT,R∑wi是R˄上优势关系相等的
AA部分,可得:
证明 略
例6 表2为一个合取型集值序信息系统,表示学生专业课能力统计信息,其中U={x1,x2,x3,x4,x5,x6}表示6个不同的学生,AT={a1,a2,a3,a4}={理论能力,实践能力,应用能力,创新能力},V={a,b,c,d}={C语言,数据库设计,计算机网络应用,数据结构},定义C语言,数据库设计,计算机网络应用,数据结构的权值分别为3,4,5,6。

表2 反映学生专业课能力的合取型集值序信息系统
定义9(优化后的粒度粗细)设一个合取型集值序信息系统S=(U,AT,V,f),∀I∈AT,∃J∈AT ,使得,则称满足优势关系优势类的集合U细于U,即I比J精细,记作 I≺J 。
例7 根据表2所给出的合取型集值序信息系统,U={x1,x2,x3,x4,x5,x6},AT={a1,a2,a3,a4},设J={a1,a2},I={a1,a2,a3},各个优势类的集合为,满足定理8,J⊆I⊆AT 则,且满足定义9
定理9 设一个合取型集值序信息系统S=(U,AT,V,f),若 I≺J ,即|,其中 ||.代表集合的基数。
5 优化后优势关系的组合熵和组合粒度
优化后优势关系的组合熵与组合粒度所满足的结论与优化前的结论是否一致,下面对优化后优势关系的组合熵和组合粒度进行讨论。
5.1 优化后的组合熵
定义10(优化后的组合熵)设一个合取型集值序信息系统S=(U,AT,V,f),∀A⊆AT 定义知识A的组合熵为0≤CE(A)<1 。 约 定 :当U/={[x]|x∈U},即优化后优势关系集合为单元素集,,此时组合熵CE(A)取最大值1。
定理10 设一个合取型集值序信息系统S=(U,AT,V,f),若 I,J⊆AT ,I≺J ,则 CE(I)≥ CE(J)。
证明 若 I≺J,由定义知,∀xi∈U ,[x]⊆,于是 CE(I)=)=CE(J),所以有I≺J ,存在CE(I)≥ CE(J)。
比较定理4和定理10,优化后优势关系组合熵与粗细程度之间关系与优化前一致。当优势关系下的集合越细时,组合熵的值也越大,集合越粗时,组合熵的值越小。
例8 根据例7可得:CE(J)=61/90,CE(I)=73/90 ,CE(I)≥ CE(J),结果与定理10一致。
5.2 优化后的组合粒度
定义11(优化后的组合粒度)设一个合取型集值序信息系统S=(U,AT,V,f),∀A⊆AT ,定义知识A的组合粒度为,则有0<CG(A)≤1。约定:当U/={[x]|x∈U}时,优化后优势关系集合为单元素集=0,此时组合粒度CG(A)取最小值0。
定理11 设一个合取型集值序信息系统S=(U,AT,V,f),若 I,J⊆AT ,I≺J ,则 CG(I)≤ CG(J)。
证明 若 I≺J,∀xi∈U ,则即,于 是 CG(I),所以有 I≺J ,存在 CG(I)≤CG(J).
例9 根据例7可得:CG(J)=29/90,CG(I)=17/90 ,CG(I)≤ CG(J),结果与定理11一致。
比较定理10和11,优化后优势关系的集合越细时,组合熵的值越大,相反组合粒度值越小;集合越粗时,组合熵的值越小,组合粒度的值反而越大,与优化前组合熵和组合粒度粗细粒度大小结论一致。
6 结语
集值信息系统是对不完备信息系统的一种拓展与延续,在现实空间中也广泛存在这类或约束条件更多的使用实例。本文在合取型集值序信息系统的二元优势关系上,引入组合熵和组合粒度对优势关系粗细程度的度量进行研究和探讨,针对满足优势关系但优势程度不同的情形进行了改进和优化,从而使改进后的优势关系更加符合实际情形,且在改进后的优势关系中,引入组合熵与组合粒度进行不确定性度量的研究,研究表明改进后的优势关系的组合熵与组合粒度之间的结论与改进前结论一致,即随着优势关系的逐步变细,其组合熵逐步递增,组合粒度逐步递减。但在实际问题中除了优势关系权值的不同,可能还会有其他条件的限制,如本文例子中,对计算机学院学生能力的合取型集值序信息系统中存在不同课程在不同时期的学习等,这都将是下一步深入研究的方向。
