稳健总体最小二乘拟合在地铁监测中的应用

陈开端

(福州地铁集团有限公司 福建福州 350001)

0 引言

福州市地处福建省东部，闽江下游沿海地带，亚热带季风气候造成的充沛降水以及闽江、乌龙江和城市内河组成的城市水系网络，使得福州市整个地下水的储备较为丰富。此外，福州市区内广泛分布有较大厚度的软土，其特点为强度低、可压缩性较高，在地面震动或者较大荷载的作用之下，容易产生固结变形，导致地面沉降，引发房屋、路面开裂等地质灾害。因此，在福州市区修建地铁是非常有难度的，必须时刻警惕坑内降水和土方开挖对坑内外水位以及路面沉降的影响。所以在地铁施工过程中，有必要采用合理的手段对施工围护结构的受力与变形、地表沉降、坑外水位以及周边环境进行数据上的监测。通过对监测数据进行分析，掌握结构的受力状态与变形状态，了解所监测对象的变形程度及变形趋势，及时发现施工过程中的安全隐患，采取相应的应急措施，保障地铁建设过程的安全稳定。

在地铁的监测过程中，由于现场施工条件问题，常常会发生监测数据因现场遮挡而产生的不连续，而为了分析监测数据的发展趋势以及修复这些不连续的情况，就需要对监测数据进行模型的构建，通过内插的方法还原不连续的数据。近年来，对监测数据进行分析的模型逐渐增多，目前常用的模型包括了曲线拟合法、灰色理论模型、卡尔曼滤波模型、人工神经网络模型、小波分析模型等。总体最小二乘曲线拟合法的基本原理是通过总体最小二乘的理论来求解曲线拟合模型中的未知参数。该方法由于同时考虑了观测值与系数矩阵的误差，因而具有无偏性，求解得到的结果精度比较高，能够有效的拟合得到监测数据的趋势模型。本文将总体最小二乘曲线拟合的方法应用于对地铁监测数据的模型构建中，并结合稳健估计的理论，提出了一种稳健的总体最小二乘曲线拟合法，在剔除监测数据中异常值的基础上，构建监测数据的趋势模型，有效预测了监测数据的发展趋势以及修复监测数据中的不连续情况。

1 稳健总体最小二乘拟合原理

1.1 最小二乘法(LS)曲线拟合法

曲线拟合法是趋势分析法中的一种，主要的原理是利用各种光滑曲线的数学模型来拟合实际数据，从而得到一个接近于真实数据变化的趋势模型。本文采用的是多项式拟合的模型，其模型方程如式(1)所示。

F(x)=a1xm+a2xm-1+…+amx+am+1

(1)

式中，a1,a2,…,am+1表示多项式拟合的系数，x为原始观测数据，m为多项式的次数。

假设总共有n个数据，则多项式拟合的误差方程可以写成式(2)的形式。

V=BX-L

(2)

其中，

(3)

则根据最小二乘的原理，可以得到待定参数的估值为：

X=(BTB)-1BTL

(4)

1.2 总体最小二乘法(TLS)曲线拟合法——(SVD法)

由式(2)、式(4)可知，最小二乘的方法在求解过程中，只考虑了观测矩阵L的误差。然而事实上，当观测数据中含有测量误差时，由观测数据所组成的系数矩阵B中也不可避免的存在误差。因此，为了能得到更加准确的结果，本文考虑了总体最小二乘的方法，将其运用到多项式曲线拟合的模型中，能够进一步提高拟合结果的精度。总体最小二乘在求解的过程中，认为系数矩阵B和观测矩阵L都包含误差，则式(2)可变形为：

(B+EB)X=L+EL

(5)

其中，EL分别由B矩阵和L向量的误差改正数组成，具体形式如下所示：

对式(5)的X的估计有多种方法，比较简单的是用奇异值分解(Singular Value Decomposition，SVD)的方法求解待定参数X的总体最小二乘解[20,23]。奇异值分解的形式如式(6)所示。

(6)

其中，

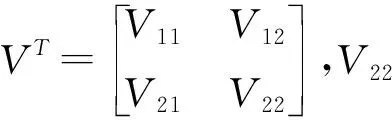
(7)

单位权中误差可根据式(8)进行计算。

(8)

其中n是样本数，f是参数数目。

由于TLS同时考虑了自变量和因变量误差，对所有需要修正的变量都进行了最小化约束，因此，利用TLS进行拟合求解不会因自变量和因变量的选择不同而产生差异，具有较LS更稳健的拟合结果[18]。

1.3 总体最小二乘法曲线拟合法(正交法)

奇异值分解的TLS将矩阵A中一列均为1的不含误差的常数矩阵进行了考虑，致使拟合结果变异。正交TLS是以所有观测点到拟合直线或平面距离的平方和最小为基准对参数进行解算，构建的算法最为合理。因此，正交TLS不仅具有较高拟合精度，同时还有较广泛的应用性。一般的[15,19,23]，多项式变换为：

F(x)=a0+a1x+a2x2+…+amxm=a0+a1X1+a2X2+…+amXm

(9)

其中X1=x,X2=x2，…,Xm=xm,

如果误差为Vx,Vy，(8)式变为：

y+Vy=a0+a1(X1+Vx1)+a2(X2+Vx2)+…+am(Xm+Vxm)

(10)

将(10)式变为正交式：

(11)

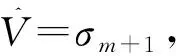
1.4 稳健的总体最小二乘曲线拟合法

有些加权总体最小二乘方法均没有考虑观测数据中可能存在粗差的情况，而现代测量手段趋向于向数据采集的自动化和快速化发展，其观测量中同时包含了粗差、系统误差和随机误差[18]。在平差处理中，如何发现和区分粗差观测量，并消除或减弱其影响，是提高平差成果精度的一个关键问题。由于地铁现场条件复杂，观测数据中会因为各种因素的影响存在粗差，因此有必要对观测数据进行粗差探测与剔除。稳健估计正是针对这一缺陷而提出来的，其目的在于构造某种估计方法，使其对于模型误差，特别是粗差具有较强的抵抗能力。稳健估计方法可以分为三大类，即M估计、L估计、R估计。本文结合了稳健估计与总体最小二乘拟合法，将二者应用于地铁监测数据的模型构建上，得到了一种稳健的总体最小二乘多项式拟合的方法，该算法的实现过程如下：

(1)利用2.2节介绍的原理进行一次总体最小二乘曲线拟合，得到参数的初始值；

(2)计算每个实际观测值与拟合值差的绝对值di；

(3)利用式(9)计算距离 的标准偏差；

(9)

(10)

(4)本文采用的稳健估计方法是由Huber在1964年提出的M-估计法，其基本思想是根据观测值残差的大小，对观测值赋予不同的权值，从而区分观测值中的粗差与正常值。根据M-估计法的准则，本文对每一个观测值的残差di进行判断，若第i个点到拟合曲线的距离di>2σ，则认为该点是异常点，应予以剔除，否则保留该点，计算式如下[21]：

(11)

(5)对经过筛选得到的观测数据再次进行总体最小二乘拟合，得到新的多项式拟合参数，完成稳健总体最小二乘拟合模型的构建。

2 实验与分析

2.1 实验方案

为验证本文提出方法的可行性，现以福州市地铁某在建工点的沉降监测数据作为实验对象。鉴于文章篇幅的限制，本文只截取其中一个沉降监测点近百日的数据进行分析，对其余各点的分析结果也基本相同。本文数据是由Trimble DINI03数字水准仪采集得到的，总共28期，具体的监测数据如表1所示。利用数据中的前20期数据进行模型拟合，并对最后1期数据进行预测，将预测得到的结果与实际数据进行比较，判断模型的预测精度。

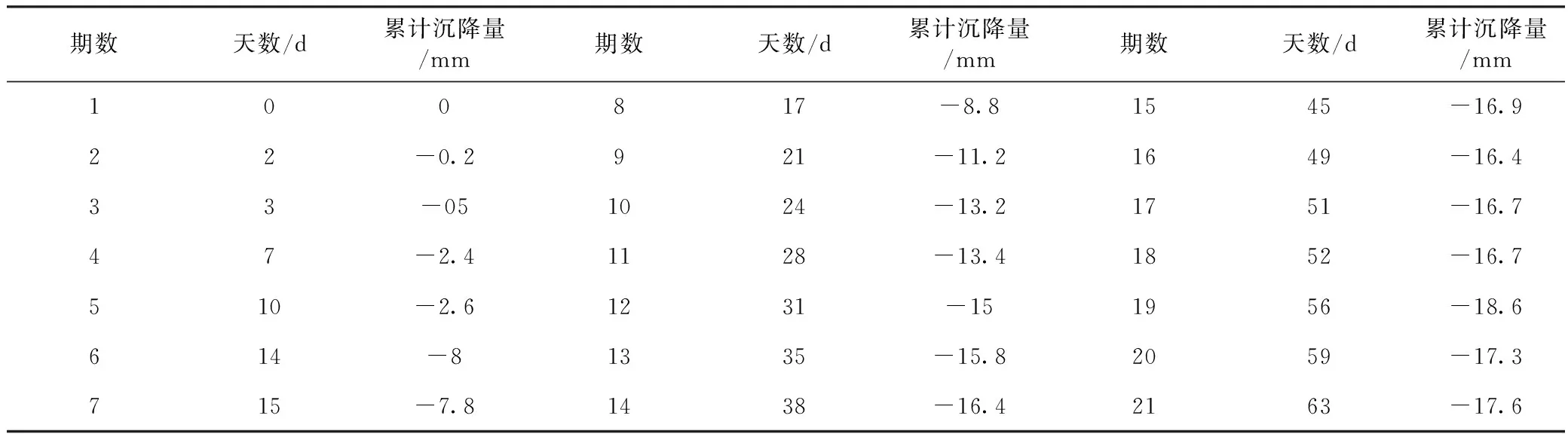
表1 原始沉降监测数据

2.2 实验分析

2.2.1最小二乘法和总体最小二乘法的比较

利用本文第二节提出的方法，对表1中数据进行最小二乘法、总体最小二乘法(SVD法,此处记为TLS1)和总体最小二乘法(正交法,此处记为TLS2)曲线拟合。根据对原始观测数据的分析，选取多项式的次数为3次。为更好地体现总体最小二乘拟合法的拟合效果，现将其与最小二乘拟合的结果进行对比分析得到的拟合结果如表2所示，第21个值最为预测检验值，计算结果如表3所示。

表2 模型拟合结果对比表

表3 模型预测结果对比表

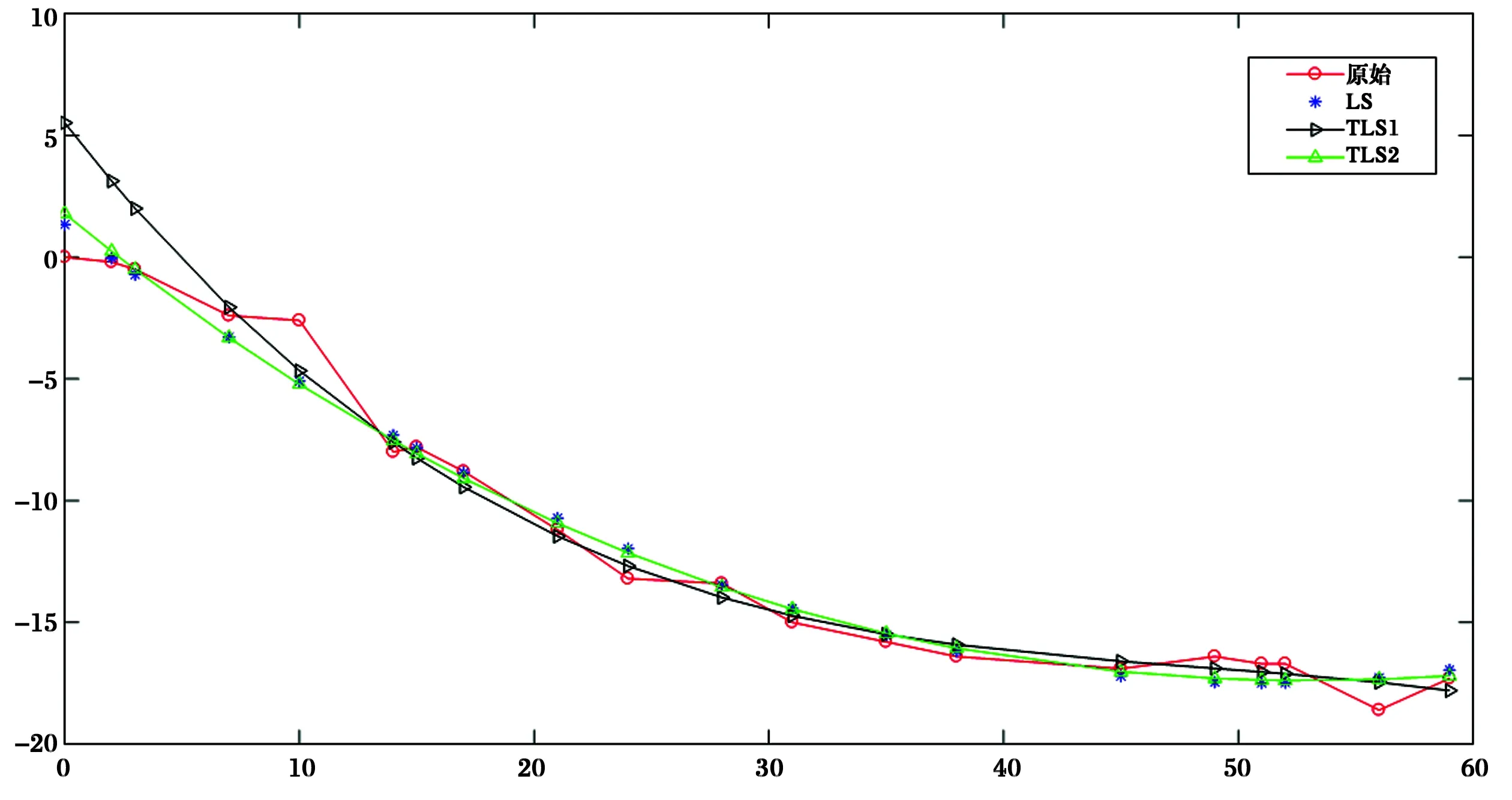
图1 LS、TLS1、TLS2拟合曲线图

由表2～表3和图1可以看出TLS所得的拟合曲线单位权中误差明显小于LS。进一步分析2种TLS的参数估计结果及精度发现，奇异值分解的TLS过多地考虑矩阵B中不存在误差的部分，致使精度明显优于其他方法，但拟合参数却已经发生变异，造成虚假的拟合误差最小现象。正交TLS考虑的是所有观测点到拟合直线距离的平方和最小，且合理地考虑了自变量和因变量误差，因此，其估计的参数更加接近实际值。综合考虑各种解的算法所得的参数及精度，可以看出正交TLS的拟合结果最优[20]。

2.2.2稳健总体最小二乘法的效果比较

根据M-估计法的准则，由Huber函数，对于残差计算出点列对应的P值如表4所示。

为更好地体现稳健总体最小二乘拟合法的拟合效果，根据表4的P值，现将在LS中去掉第1个、第5个、第10个、第19个异常点，在TLS1中去掉第1个、第2个，在TLS2中去掉第1个、第5个异常点，分别进行稳健总体二乘法，得到结果如表5所示。

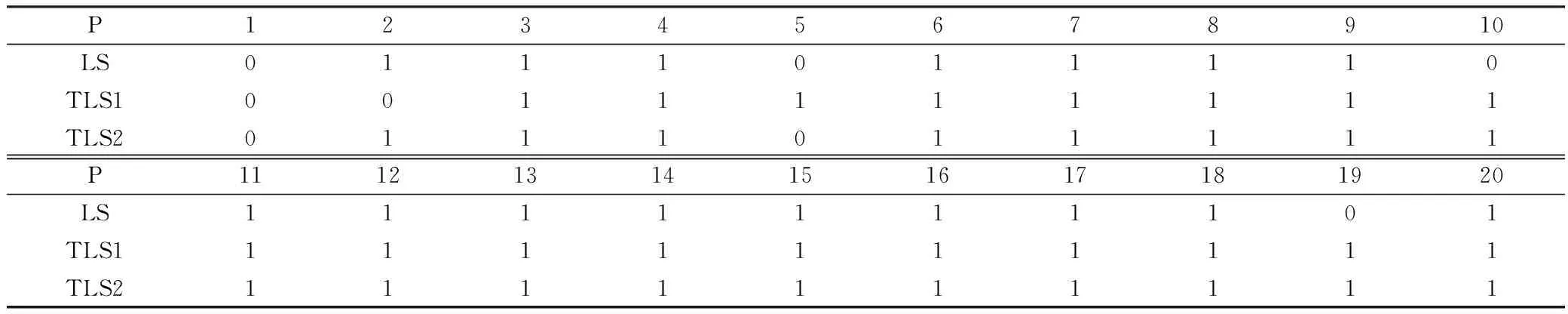
表4 三种拟合P值表

表5 模型拟合结果对比表

表6 模型预测结果对比表

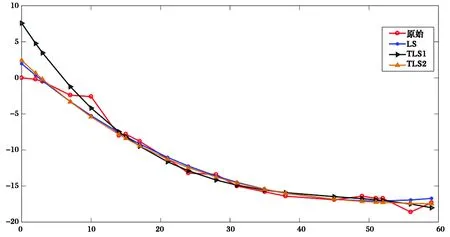
图2 稳健加权后的 LS、TLS1、TLS2拟合曲线图拟合曲线图

将由表4～表5和图2与表2～表3和图1相比较，明显稳健加权总体最小二乘法比总体最小二乘法和最小二乘法效果好得多。最小二乘拟合模型的验后单位权中误差为0.9 939mm，本文模型的验后单位权中误差分别为为0.21mm和0.49mm，3种方法的拟合曲线图如图2所示。从图2中可以发现，3种方法基本都能拟合原始观测数据的发展趋势，本文提出方法的拟合效果相比最小二乘拟合法会更佳，特别是正交法更佳。由表6可以发现，稳健总体最小二乘拟合法的预测结果，其平均绝对误差和平均相对误差都小于最小二乘拟合法的预测结果，预测结果与实际值的误差分别为0.4mm和 0.15mm，都在1mm以内，能够满足地铁监测的要求。因此，稳健总体最小二乘拟合法，特别是使用正交法的稳健总体最小二乘拟合法，较一般的最小二乘曲线拟合法而言，具有相对高的拟合、预测精度，预测结果稳定可靠，比较适用于地铁的施工监测过程中。

3 结论

本文利用稳健估计结合总体最小二乘的方法，对福州地铁某工程沉降监测数据进行了多项式曲线拟合，并对实测数据进行预测。结果显示，稳健总体最小二乘拟合法能较好地拟合监测数据的发展趋势，其预测结果相比一般的最小二乘拟合法而言，绝对误差和相对误差都较小，预测结果能控制在1mm以内，能够满足地铁施工监测的要求，因而对短期预测施工监测数据的发展趋势有较大的帮助，有一定的实际应用价值。