归宗悟理 建模解惑

骆星驰

（福建省泉州台商投资区玉坂小学，福建泉州 362100）

引 言

在日常的课堂教学中，客观存在很多知识点的讲解与探索体验，但学生往往停留在知其然而不知其所以然的阶段，师云亦云，生搬硬套，对知识点的“前世、今生、发展”没有纵向打通，缺乏横向拓展，教师未能引导学生归宗悟理，建模解惑，降低了学生学习的有效性和可持续性[1]。其实，小学数学中有些知识点可以归宗为整数乘除法的意义来加以理解、应用，学生对知识点悟通明理后，方能掌握得持久。

一、求几个几的和是多少的模型应用

在小学数学知识点中，有求路程、求总价、乘法分配律、解决“美元兑人民币”等问题。在学习过程中，教师可引导学生把此类问题进行“类比”，归宗为“整数乘法的意义”的应用，即求几个相同加数的和的简便运算，从学生的认知水平和已有经验出发，化难为易，进行迁移，借旧学新。

针对以上问题，在新课伊始，教师要充分铺垫，唤醒学生的已有经验。可出示3+3+3+3+3+3=( )×( )个，学生大多能脱口而出，5 个3 相加的和等于3×5，教师可追问：一般谁写在乘号前面，表示什么？（相同加数）乘号后面的数表示什么？（相同加数的个数）教师还可以在开始学习时强调并规定，把相同的加数放在乘号前面，相同加数的个数放在乘号后面。

例如，在教学北师大版小学数学四年级上册《路程、时间与速度》一课想一想、填一填中的求路程问题时，教师可以先引导学生分析已知条件和问题，然后让学生把图意口述编成一道完整的应用题：淘气从学校到少年宫每分钟走60 米，用了10 分钟，从学校到少年宫的路程是多少米？教师引发学生思考：求什么？怎么求？请尝试列式计算。当学生初步回答求的是路程，路程=速度×时间，60×10=600（米）后，教师要继续追问：为什么列式是60×10 而不是其他？学生讨论并发表意见后，可让一名学生上台演示，走1 步代表1 分钟走60 米，台下学生喊10 个1 分钟，台上学生走10 步，教师乘机提问：“他一共走了几个几？”这时学生们纷纷喊出10个60，师又问：“10 个60 怎么列式表示？”学生有了课堂开始的铺垫，基本上会说出求10 个60，列式为60×10。教师再一次强调，表示个数的10 要写在乘号后面，相同的60 米/分要写在乘号前面，然后从60×10=600（米）中再次追问学生60 表示什么？10 表示什么？600 表示什么？直观地一一对应，导出60(速度) × 10 (时间) =600（米）（路程）；反之亦然，路程=速度×时间。

再如，在教学北师大版四年级上册《乘法分配律》一课中问题串（四）时：请结合4×9+6×9 这个算式，说明乘法分配律是成立的，除了课本的提示方法外，也可以把它转化为整数乘法意义的模型来理解并加以解决，即把4×9+6×9 变形为9×4+9×6=9×4 个+9×6 个=9×(4+6)个 = 9×10 个=90。初始学习乘法分配律时，暂且先应用乘法交换律转化为相同的加数在乘号前面，相同加数的个数在乘号后面的统一模型，便于学生借助于整数乘法的意义理解算理。

又如，在教学北师大版五年级上册《人民币兑换》一课中问题串（一）时：美国小朋友玛丽给笑笑寄了1 本故事书，书的单价是6.70 美元，折合人民币多少元？（1 美元兑换人民币6.31 元）当学生尝试独立计算并讨论后，教师可“类比”运用整数乘法的意义模型，引导学生理解美元兑换人民币的解决方法和算理。为什么用6.31×6.7 而不用除法或其他方法计算？因为1 美元兑换人民币6.31 元，2 美元兑换2 个6.31元人民币，3 美元兑换3 个6.31 元人民币……类似地，6.7 美元可兑换6.7 个6.31 元人民币，所以“美元兑人民币问题”可转化为类似求几个几的总和问题，因此要用乘法解决，列式时仍然要强调表示个数的数写在乘号后面。

二、包含除的模型应用

在小学数学学习中，求时间、数量（份数）、“人民币兑换美元”等典型问题，都可以用包含除来理解并加以解决。

同样地，在新课铺垫环节，教师可以先借助于学生的已有经验，如从简单的生活问题入手，让学生思考并回答：100元人民币可换几张20 元的？怎么列式解决？100÷20=5（张）。为什么是5 张呢？100 里面包含了几个20？唤醒学生明白100 里面包含了5 个20，为新课的学习做好铺垫。

例如，在教学北师大版四年级上册《路程、时间与速度》中试一试问题串（一）求时间时，当学生理解题意以后，可让学生口头编述应用题：甲、乙两地相距140 千米，汽车每小时行驶70 千米，从甲地到乙地需要多少小时？教师先让学生思考求什么？怎么求？先尝试独立列式解答，接着让学生互相讨论为什么要这样列式？说说理由，并让一名学生上台演示，假定学生两大步远的距离为140 千米，学生走1 步代表1 小时行70 千米，学生走了2 步（2 个70 千米）到达乙地，让学生想想并说说140 千米里面包含了几个70 千米？结合线段图，直观地理解140 千米里面包含了2 个70 千米，140÷70=2，所以是2 小时，从而一一对应理解“路程÷速度=时间”；反之亦然，时间=路程÷速度。

再如，在教学北师大版五年级上册《人民币兑换美元》中的问题串（二）时：妈妈用600 元人民币可兑换多少美元？（1 美元兑换人民币6.31 元）教师可以引导学生理解题意为：把600 元人民币，分成若干份装进红包，每个红包装6.31 元人民币，这样每个红包里的6.31 元人民币兑1 美元，看看600 元人民币里面包含了几个6.31 元人民币，便是几美元。应用包含除模型列式为600÷6.31，用“讲道理”的教学方式相乘除或相加减，避免学生不知从何下手。

三、平均分的模型应用

小学生对“平均分”相对容易理解，为了加深学生对“平均分”的理解，可让学生上台模拟表演拔河比赛，首先故意安排3 个人对阵5 个人，这时学生会抗议安排不公平。为了公平要怎么调节呢？4 个人对阵4 个人（忽略胖瘦高矮），让学生充分理解平均分的含义，即每份数要相同。

在教学速度、单价、平均数（每份数）、耗油量、工作效率等典型问题时要用到平均分。以北师大版四年级上册《路程、时间与速度》一课中“猜一猜，谁走得快？”的教学为例。

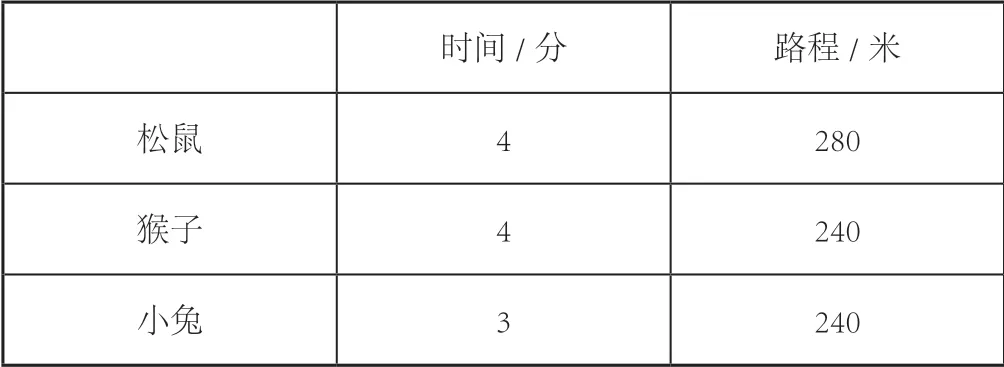
表1 竞走成绩表

首先出示竞走成绩表（见表1），引导学生观察得出“时间相同比路程”，路程长的速度快；“路程相同比时间”，时间少的反而快。接着是比较小兔和小松鼠谁更快，猜一猜路程不同时间也不同，无法直接比较怎么办？只好比较它们在单位时间里谁走得快，借助于线段图进行直观比较，体会到小兔走得快。通过平均分得出：小兔的速度为：240÷3=80（米/分）；松鼠的速度为：280÷4=70（米/分），80 米/分＞70 米/分，答：小兔走得快。

结 语

由此可见，在小学数学教学中，教师要引导学生归宗悟理，建模解惑，这样才能提高学生学习的有效性和可持续性。今后，笔者会继续践行“讲道理”的数学，努力做一名“讲道理的数学教师”。