Nonlinear behavior of the population dynamics of three-level systems in the presence of single photon absorption
2019-02-25AllamSrinivasaRao
Allam Srinivasa Rao
Photonic Sciences Laboratory,Physical Research Laboratory,Thaltej,Ahmedabad,Gujarat 380059,India
Keywords:nano-second laser,pico-second laser,nonlinear absorption,z-scan
1.Introduction
In recent decades,nonlinear absorption spectroscopy has widely been used to estimate spectroscopic parameters.The advantage of nonlinear absorption spectroscopy over linear absorption spectroscopy is that one can estimate the excited states properties,where the linear absorption transitions are forbidden by dipole transition selection rules. Depending upon the material’s characteristics,such as absorption crosssection and lifetime of excited states,their optical properties have to be studied in different time scale laser illuminations using cw,[1,2]nanosecond,[3,4]pico-second,[5-7]and femtosecond[6-8]lasers.The wide range of temporal modulations in the laser beam’s power(range from cw to atto-second)enhanced their applications in a broad range of science.[9-11]To make the best use of them in the point of spectroscopic applications,we should know the effect of laser beam temporal profile on the absorption.
The nonlinear absorption is determined by the volume of the material interacting with the probing laser beam,the incident laser pulse width,repetition rate,and energy.The cw and long pulse width lasers limited the experiments on nonlinear absorption and their applications[12-16]due to thermal effects and low nonlinear absorption coefficients of materials.Using a pulsed laser,[17,18]the absorption nonlinearity at low average power can be studied without any thermal effects.The nonlinear absorption analysis with short pulses is often accompanied by laser pulses repetition rate.Consequently,the repetition rate plays a key role in a nonlinear absorption study.While repetition rate apprises the next pulse arrival to excite the sample,the life-time of the excited states determines the number of absorption species(molecules/atoms)present in the excited state at a given time.Thus,it is important to include pulse width along with the pulse repetition rate when studying nonlinearabsorption.This article focuseson the effectofthe pulse width and its repetition rate on optical energy absorption.The reason behind the study of single laser pulse excitation of material is to understand the transient decay of optical energy.In recent years,much experimental work has been carried out on the study of transient life time spectroscopy in a single pulse excitation.[19-24]Our theoretical results can be directly used in both short pulse and long pulse excitation cases.The numerical simulation results of population dynamics in the time domain are further used to discuss the z-scan[25]absorption curves.
Materials can be classified into two main categories based on their optical absorptive properties,namely non-cascade systems and cascade systems.[26]The time-dependent populations in three level non-cascade and cascade systems under pico-,and nano-second laser pulses excitation are discussed in Sections 2 and 3,respectively.The intensity of Gaussianshaped temporal profile laser pulse can be written as
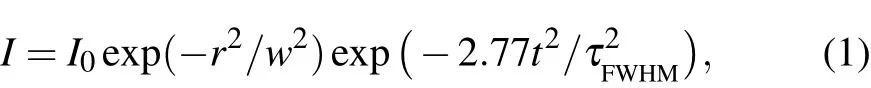
where,I0is the peak intensity,w is beam spot size,and τFWHMis the full width at half maximum(FWHM)of the laser pulse.The time-dependent populations can be studied with the rate equation technique[27-30]under the non-steady state condition.The photon flux intensity used in this article is 1017photons/s·cm2.
2.Three-level non-cascade system
The three-level non-cascade system is consists of one triplet and two singlet states.[31]While singlet states decay with fluorescence lifetime,triplet states decay with the phosphorescence lifetime.The schematic energy level diagram of three-level non-cascade system is shown in the inset of Fig.1.The transition from the ground state to the triplet state is forbidden by the dipole selection rule.In non-cascade energy levels,the time taken to finish a complete absorption process is longer than in cascade energy level systems due to meta-stable nature of triplet states.Consequently,non-cascade systems saturate at low intensities when compared with cascade systems.The population transfer and their redistribution among three energy levels can be understood by Eqs.(2a)-(2d).In these equations:Niis the number density of absorption species in the i-th state.The total number density of molecules N=∑Niand the fractional number density of each state is given by ni=Ni/N,which satis fies the condition∑ni=1.The absorption cross-section from the i-th level to the j-th level is σijand the decay time from the j-th level to the i-th level is τji.

The rate equations(2b),(2c),and(2d)give the respective rates of change of population in the 0-th,1st,and 2nd states.Throughout the population dynamics,the absorption species in the light-matter interaction volume satis fies the condition given in Eq.(2a).The time-dependent population in each energy level is obtained by numerically solving the coupled rate Eqs.(2b)-(2c)constrained by a condition given in Eq.(2a).
Figure 1 depicts the time-dependent population in the three-level non-cascade system in the presence of single-shot 100-ps laser pulse.The green curve represents the distribution of fluence(F)in the temporal realm.In time scale,the medium excited with a laser pulse with its central peak at t=50×10-10s.The initial conditions of population in the ground, first,and second excited states are n0(t=0)=1,n1(t=0)=0,and n2(t=0)=0 respectively.We can see the population dynamicsas:afterinitiating the excitation,the population in the ground state(n0)drastically decreased within the laser pulse domain and correspondingly one can see the population accumulated in the first excited state(n1)in the same vicinity.Due to the large inter-system crossing rate between the excited singlet(|2〉)and triplet state(|1〉),the pump population from ground state to the singlet state is transferred to the triplet state with a fast decay time(τ21=10-11s).Consequently,population in the excited singlet state,n2≈0.After laser pulse excitation,the population decay from the triplet state depends purely on its lifetime(τ10=10-6s).In the present experimental parameters at t=10-4s,the population in the triplet state completely decays to the ground state,i.e.,n1(t=10-4s)=0,and n0(t=10-4s)=1.

Fig.1.Population dynamics in the energy levels of the three-level noncascade system at 100-ps single laser pulse excitation for material parameters:σ02=10-17 cm2,τ10=10-6 s,τ20=10-9 s,and τ21=10-11 s.
The population dynamics of three-level non-cascade system under single 100-ns laser pulse excitation is illustrated in Fig.2.The central peak of the laser pulse is at t=50×10-8s.Even though excited with equal fluences enveloped by 100-ps and 100-ns laser pulses,due to the large peak power of 100-ps pulse with reference to 100-ns pulse,the depletion in the ground state population in the case of ps pulse excitation(Fig.1)is larger than the ns pulse(Fig.2).However,one can still see the considerable absorption present in the nanosecond laser pulse excitation.Thus,non-cascade systems can be used as a good nonlinear optical material for long pulse lasers at high average power.

Fig.2.Population dynamics in the energy levels of the three-level noncascade system at 100-ns single laser pulse excitation for material parameters:σ02=10-17 cm2,τ10=10-6 s,τ20=10-9 s,and τ21=10-11 s.
To investigate the effect of one pulse on its next pulse transmittance,the population dynamics in two-pulse excitation are graphically illustrated in Fig.3.Two 100-ps laser pulses are used to excite the medium at t1=50×10-10s with the first pulse and at t2=1.25×10-8s with the second pulse.Repetition time of pulses is tr=t2-t1=1.25×10-8s(80 MHz).The first pulse-generated population in the excited state is already shown in Fig.1.The second pulse arrival is within the decay time of triplet state lifetime(τ10)and the second pulse excited the un-depleted population of the ground state.Consequently,the population in the triplet increased after second pulse excitation.To show the entire transmittance curve,we used logarithmic time scale and due to this second laser pulse being at t2=1.25×10-8s,we were not able to resolve its shape.The clear shape of second pulse in the resolved time scale can be seen in the inset of Fig.3.

Fig.3.Population dynamics in the energy levels in the presence of two-100-ps-laser-pulses excitation for material parameters:σ02=10-17 cm2,τ10=10-6 s,τ20=10-9 s,and τ21=10-11 s.
As shown in Fig.3,in the presence of a finite population in the excited state,the depletion in the ground state reduced the absorption of light energy from the second pulse.Thus,the nonlinear transmittance curves behavior varies with the repetition rate.This leads to the uncertainty in the spectroscopic parameters extraction from the theoretical fit of transmittance curves.Therefore,it is necessary to consider the effect of repetition rate in the theoretical transmittance curve.As shown in Fig.4,the z-scan transmittance curve(open aperture z-scan)is analyzed as a function of number pulses interacted with the medium for laser pulse and material specifications used in Fig.3.The sample thickness and Rayleigh length used in the simulation are 100µm and 1 mm,respectively.In the single pulse excitation,all absorption species are present in the ground state.Hence,the ratio of the number of transmitted photons to the numberofincidentphotons completely depends on the excited states lifetime(blue line).In the presence of two pulse excitation,while the first pulse transmittance follows as the blue line,the second pulse sees the depleted ground state population.Consequently,the ratio of the number of transmitted photons to the number of incident photons is relatively much larger in the second pulse when compared with the first pulse.Consequently,the average two pulse transmittance is substantially large as compared with the single pulse excitation.A further increase in the number of pulses in the excitation process decreases the rate of increase in the transmittance due to saturation.In the present study,the z-scan transmittance curve saturates at four pulses excitation and has not seen any further increase in the z-scan transmittance with increasing the number of excitation pulses.In the presence of 1-kHz repetition rate laser pulse excitation,irrespective of the number of laser pulses excitations,the z-scan transmittance curve stays constant(it is equal to blue line in Fig.4)because the population from the excited state decays to ground state due to the first pulse before next pulse interacting with the medium.In this case,single pulse contribution in the absorption is enough to use in the z-scan transmittance curve to accurately extract the spectroscopic parameters.In a similar manner,one can see the same kind of changes in the z-scan transmittance curve for reverse saturable absorption/optical limiting.

Fig.4.The z-scan curve for different numbers of femto-second pulses excitations:σ02=10-17 cm2,τ10=10-6 s,τ20=10-9 s,and τ21=10-11 s.
3.Three-level cascade system
Three-level cascade systems[32-35]contain three energy levels,and the absorption and the emission takes place in a cascade.The energy level diagram of the three-level cascade system is given in the inset of Fig.5.The differential equation forms of population distribution among each energy level are given in Eqs.(3a)-(3d).

Figure 5 shows the time-dependent population in the three-level cascade system in the presence of single-shot 100-ps laser pulse,such as in a non-cascade system(Fig.1).In identical laser pulse excitation,the population decay in the three-level cascade system(Fig.5)is faster when compared with three-level non-cascade system(Fig.1)due to fast fluorescence decay time.The population in the second excited state(n2)is less than the population in the ground state(n1)because of σ01=10-16cm2> σ12=10-17cm2.In this case,the system acts as a saturable absorber and the z-scan curve has the form as shown in Fig.4.In another case(σ01<σ12),it is reverse saturable absorption and the z-scan curve will have the dip instead of a peak in the transmittance curve.Due to the negligible contribution from the second excited state in the absorption process,the transmittance curve is insensitive to the excited state absorption cross-section(σ12)and lifetime(τ21).It is inferred that to accurately measure the second excited state spectroscopic parameters,we have to use low repetition rate and high peak power ultra-short laser pulses while avoiding thermal damage;i.e.,single shot laser pulse excitation.[30]Fast decay allows cascade systems to use efficient optical limiters and saturable absorbers in ultra-short time scale laser pulses.
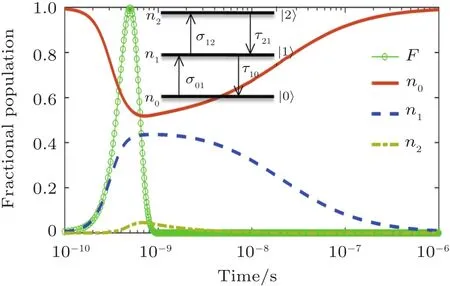
Fig.5.Population dynamics in the energy levels at 100-ps single laser pulse excitation for material parameters: σ01=10-16 cm2,σ12=10-17 cm2,τ10=10-9 s,and τ21=10-10 s.
Figure 6 illustrates the population distribution as a function of time under 100-ns single laser pulse excitation.The population depletion in the ground state is very low and these systems show considerably less absorption nonlinear optical properties in the ns and cw laser excitation when compared with non-cascade energy level materials.However,a pure optical nonlinear study(without thermal nonlinear contribution)in the cascade systems is not possible in the ns and cw laser illumination.

Fig.6.Population dynamics in the energy levels at 100-ns single laser pulse excitation for material parameters: σ01=10-16 cm2,σ12=10-17 cm2,τ10=10-9 s,and τ21=10-10 s.
4.Conclusion
We have demonstrated the effect of repetition rate on the nonlinear transmittance curve in the z-scan technique.Laser pulses with a width of 100 ns and 100 ps are chosen to study the population dynamics to show the population dynamics in long pulse and short pulse cases.In addition,we show how the peak intensity variation with pulse width plays a key role in population dynamics.The light-matter interaction is completely different in the long pulse excitation and short pulse excitation.For example,organic dye molecules[2]in the presence of their singlet and triplet states,while they act as noncascade energy level systems in the presence of long pulse excitation(Section 2),[4]in the presence of short pulse excitation become cascade systems(Section 3).[30]While non-cascade systems are good nonlinear optical materials in the cw and ns due to their large triplet lifetimes,cascade systems can be used as efficient optical nonlinear media in ultra-fast time scale absorptions.Depending upon the material’s spectroscopic parameters with respect to laser beam parameters,one has to choose a proper medium as saturable absorber/optical limiter for a given laser.These discussions can intrigue nonspecialists in the time domain nonlinear spectroscopy in the sense of understanding the temporal effects of laser pulses.Even though our numerical results of population dynamics in the presence of single pulse excitation cannot be seen directly in the experiment,we can be use them in the transient spectroscopy,pump-probe spectroscopy and z-scan.[36-43]In addition,using our single and multiple pulses excitation,one can understand the population dynamics in the presence of life times and absorption cross-sections.In the present article,time-dynamics are completely devoted to saturable absorption to understand the population dynamics of saturable absorbers and can be used to understand the basic phenomena in the qswitching pulse generation using saturable absorbers.[44-46]In a similar manner,one can study the population dynamics in reverse saturable absorption.
杂志排行
Chinese Physics B的其它文章
- Superlubricity enabled dry transfer of non-encapsulated graphene∗
- Synthesis and characterization of β-Ga2O3@GaN nanowires∗
- Low-energy(40 keV)proton irradiation of YBa2Cu3O7-x thin films:Micro-Raman characterization and electrical transport properties∗
- Preliminary investigation on electrothermal instabilities in early phases of cylindrical foil implosions on primary test stand facility∗
- Effects of secondary electron emission on plasma characteristics in dual-frequency atmospheric pressure helium discharge by fluid modeling∗
- In fluence of low-temperature sul fidation on the structure of ZnS thin films∗
