平衡鼓间隙对首级叶轮前泵腔压力及多级泵轴向力的影响

钱 晨，杨从新，富 友，张 扬，侯凯文



平衡鼓间隙对首级叶轮前泵腔压力及多级泵轴向力的影响

钱 晨，杨从新，富 友，张 扬，侯凯文

（兰州理工大学能源与动力工程学院，兰州 730050）

平衡鼓的轴向力平衡能力是多级离心泵发生故障并影响其寿命的关键因素。该文采用数值模拟方法，在多级泵的外特性、平衡管内压力和泄漏量的数值计算结果与试验结果基本一致的基础上，研究了平衡鼓间隙泄漏量变化对首级叶轮前泵腔的压力分布、首级叶轮及整个叶轮轴向力的影响。研究结果表明：首级叶轮前泵腔中的漩涡区是腔体内压力变化的主要原因。当平衡鼓间隙由0增大到0.5 mm时，首级叶轮的轴向力在间隙为0时最大，在间隙为0.3 mm时最小，其最小值为最大值的20.6%；整个叶轮所受轴向力随着平衡鼓间隙增大呈先减小后增大的趋势。无量纲化的平衡鼓间隙面积大于6.6×10-3时，由于平衡鼓前后压差较小，已无法有效平衡轴向力，在此范围轴承发生断轴的风险较大。该研究可为多级泵平衡鼓设计提供参考。

泵；压力；数值计算；首级叶轮前泵腔；平衡鼓间隙；轴向力

0 引 言

多级离心泵轴向力过大直接影响其运行稳定性，平衡和减小轴向力是目前研究多级离心泵的重要课题之一。多级泵的轴向力平衡装置主要有平衡盘和平衡鼓等，由于平衡鼓没有与动静金属直接接触，其运行可靠性较高，被广泛应用在节段式多级离心泵轴向力平衡机构中[1]。平衡鼓的工作原理是通过末级叶轮后泵腔与平衡腔之间的压差平衡轴向力[2]。平衡鼓在运行过程中，由于长期受到液体的碰撞或与壳体发生摩擦，平衡鼓间隙产生磨损，使平衡鼓间隙泄漏量逐渐增大[1-3]。而平衡鼓间隙泄漏流通过平衡腔底部的平衡管与吸水室相连，其间隙大小对首级叶轮前泵腔进口流量产生影响，引起首级叶轮前泵腔压力的改变[4-8]。

许多学者在平衡鼓轴向力平衡及平衡鼓间隙泄漏流方面做出了研究。Gordon 等[9]揭示了预旋和转子涡流速度对阶梯式和锯齿状平衡鼓间隙泄漏量的影响。Rui 等[10]通过试验和数值模拟方法分析了空化导致的平衡腔侵蚀引起平衡鼓间隙压力及流量的变化。张贤安等[11-12]通过单独对平衡鼓进行数值模拟，发现随着平衡鼓间隙增大，平衡鼓轴向力平衡能力迅速减弱。张翼飞等[13]通过试验方法确定了平衡鼓直径的大小。此外，许多学者在平衡鼓优化设计上也做了许多工作[14-17]。从上述研究中可以发现，关于平衡鼓的研究都只侧重于间隙流动对平衡鼓受力等局部特性的影响，而关于平衡鼓间隙泄漏量对首级叶轮前泵腔腔体内流动特性、首级叶轮和整个叶轮轴向力以及对平衡鼓轴向力平衡能力影响的研究尚未开展，因此，有必要对上述问题进行深入研究。

本文以兰州某石化公司助剂厂使用的高压双壳体11级节段式多级离心泵为研究对象，通过改变平衡鼓间隙大小，进行全流场数值计算，研究不同工况下，平衡鼓间隙对首级叶轮前泵腔流体的运动及压力分布、首级叶轮及整个叶轮轴向力的变化，同时将数值计算结果与试验结果进行比较，并分析了残余轴向力系数与比面积的关系，得到多级泵轴承发生断裂风险较大的范围。

1 模型与数值方法

本文选用的P101A型节段式多级离心泵，其主要设计参数为：设计流量=128 m3/h，级数=11级，单级扬程=106 m，转速=2 986 r/min，其过流部件主要参数如表1所示。应用Pro/E软件进行全流道几何建模，如图1所示。本文在原型泵平衡鼓间隙为0.2 mm的基础上，进行5次平衡鼓间隙的改变，分别为0、0.1、0.3、0.4、0.5 mm。

采用六面体结构化网格进行多级泵全流道数值仿真，并对近壁区进行网格加密，近壁区+（靠近壁面第一层网格的无量纲高度）小于5。选择效率作为准则来进行网格无关性验证，设计工况点泵效率和网格关系如图2所示，当网格数从4 800万增加到6 500万时，泵的效率绝对值增量小于0.01%，故采用4 800万网格进行数值计算如图2所示。部分部件网格图如图3所示。对于耦合面上网格尺度差异较大的区域，采用等比递增的网格划分形式，使网格合理过渡。

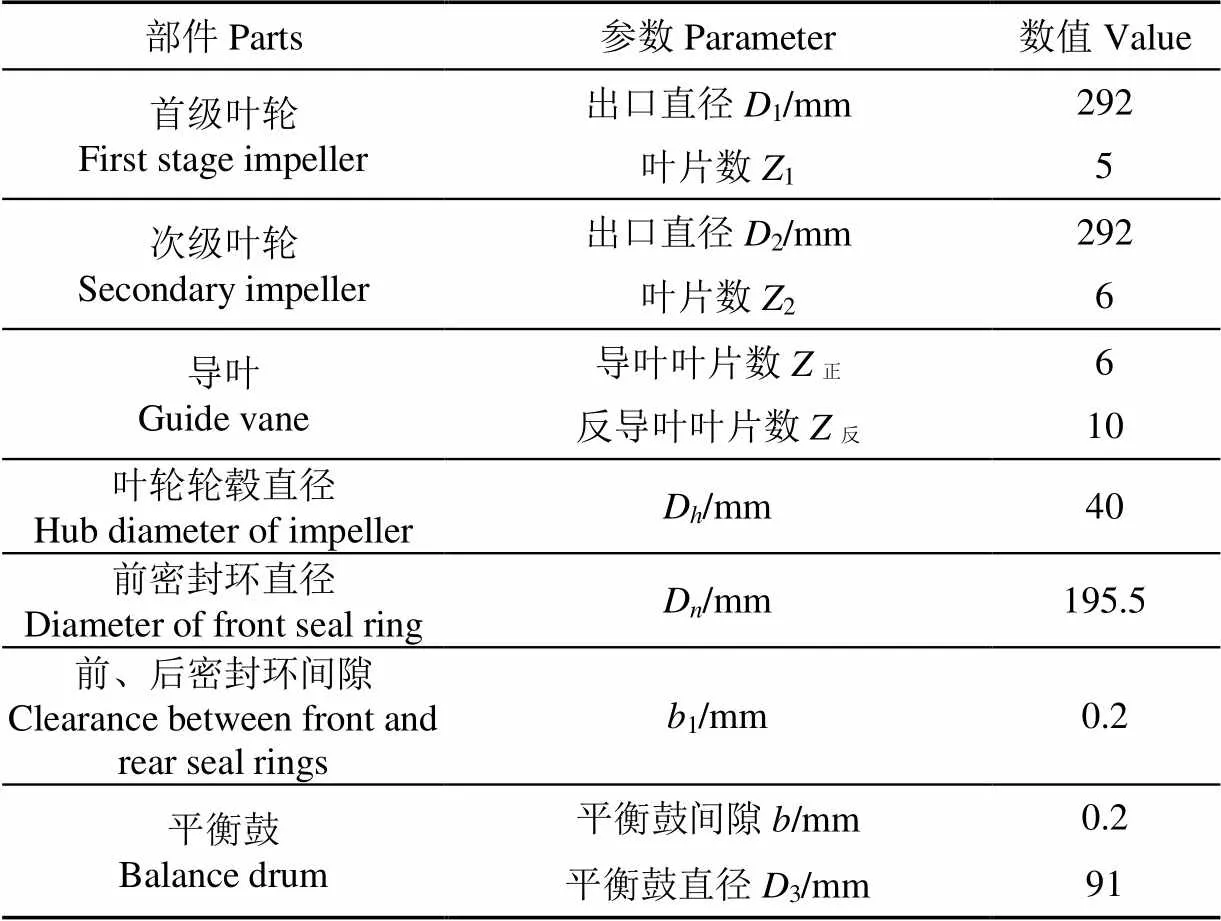
表1 多级泵过流部件主要参数

1.吸水室 2.首级叶轮 3.导叶 4.次级叶轮 5.末级导叶 6.压水室 7.平衡管 8.末级叶轮后盖板 9.平衡腔 10.平衡鼓间隙

1.Suction chamber 2.First stage impeller 3.Guide vane 4.Secondary impeller 5.Final stage guide vane 6.Water chamber 7.Balance tube 8.Rear cover plate of last stage impeller 9.Balance chamber 10.Balance drum clearance

注：1为首级叶轮出口直径，mm；D为前密封环直径，mm。

Note:1is the outlet diameter of the first impeller, mm;Dis the diameter of front seal ring, mm.

图1 多级泵计算模型

Fig.1 Computational model of multistage pump

利用FLUENT流体计算软件，将工作介质选取为清水，泵内流动设置为不可压缩定常湍流流动。应用SST-湍流模型，进口边界条件为速度进口，假定来流方向垂直于入口截面，给定来流速度的大小。出口边界为自由出流，认为流动充分发展，固体壁面给定无滑移条件。

图2 不同网格数下的泵效率

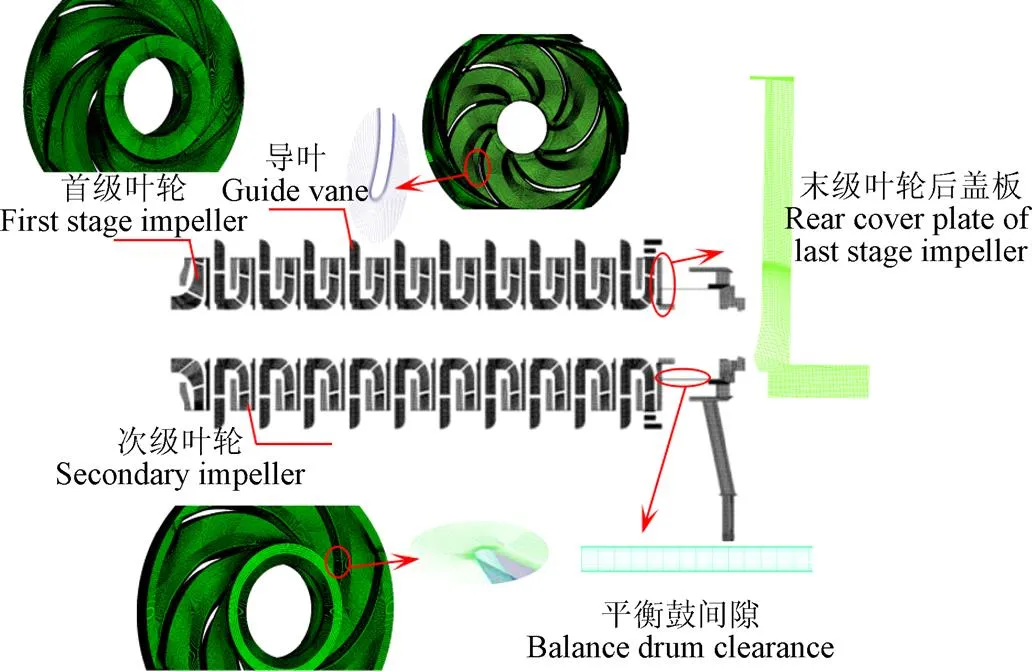
图3 多级泵网格图

2 模拟结果与试验验证

试验是在兰州石化公司助剂厂P101A泵的试验台进行，试验测试装置如图4所示。多级泵试验台是甲乙酮反应装置的一部分，试验泵主要将回流罐中的液体输送到填料塔进行氧化还原反应。试验台使用的电机为AMD400L2RBABM型电机（瑞士ABB公司）提供的最大功率为455 kW，可以满足泵运行的设计转速2 950 r/min；泵的进、出口液体压力用德国西门子公司的7MF403压力传感器测量，其测量误差为±0.075%；采用中国横河公司AE215型电磁流量计测量流量，其测量误差为±0.5%；转速与功率用安装在泵与电机之间的转速转矩传感器测量[18-20]。

1.泵出口 2.泵进口 3.扭矩仪 4.电机 5.试验多级泵 6.压力计 7.孔板流量计

在平衡管轴向距泵进口153 mm处安装上海蒙晖公司的MH6150型孔板流量计（0.5级）测流量，在239 mm处安装上海自动化仪表四厂生产的YB-150型标准压力计（0.4级）测压强。试验时，先从设计流量（128 m3/h）以20 m3/h量级逐渐递减到最小流量28 m3/h，后逐级递增大到最大流量248 m3/h，最后逐级调整为设计流量为一个试验周期。试验数据为同一流量下一个试验周期2次试验结果的平均值，试验与数值计算结果如图5所示。

图5 多级泵试验结果与数值模拟结果对比

从图5a可以看出，数值预测性能曲线与试验曲线变化基本一致，但模拟值始终低于试验值，这是主要由于数值模拟没有考虑机械密封和轴承摩擦所产生的能量损失，其中扬程、效率、轴功率的最大误差分别为4.17%、2.81%和4.25%。

对于高压双壳体多级泵而言，直接测量泵腔内的压强及平衡鼓间隙泄漏量的难度较大，因此本文通过测量平衡管内的压强及流量，并与模拟结果进行比较，从而验证文中采用的计算方法的可靠性。从图5b中可以看出，平衡管流量的计算值与试验值趋势基本一致，但试验值始终小于模拟值，这主要因为数值模拟没有考虑孔板流量计对管道内流动的影响，设计工况点平衡管流量最大误差为4.49%。平衡管内压强的计算曲线与试验曲线吻合较好，最大误差为2.5%，试验误差在允许范围内，说明本文选用的计算方法能够为本研究提供可靠保证。

3 数值计算结果及分析

3.1 首级叶轮前腔体压力分布

为分析平衡鼓间隙变化与首级叶轮前泵腔压力的关系，在设计流量下，分别截取多级泵首级叶轮前泵腔沿轴向的3个截面（如图1b所示）分别为：前泵腔进口截面（1-1截面）、前泵腔轴向中心截面（2-2截面）以及前泵腔出口截面（3-3截面），其压力云图从左至右如图6所示。

从压力云图6上可以看出，同一平衡鼓间隙下，首级叶轮前泵腔内液体压力由叶轮前泵腔进口截面至前泵腔出口截面沿轴向压力呈逐渐增大的趋势，这是因为腔体内的液体受到首级叶轮前盖板旋转影响，压力从进口至出口逐渐增大[21-26]。当平衡鼓间隙由0～0.5 mm增大时，首级叶轮前泵腔体内各截面的压力沿径向逐渐增大，尤其在前泵腔出口截面尤为明显，这是因为随着平衡鼓间隙增大，通过平衡管流入吸水室液体的压力增加，导致首级叶轮进口截面压力增大，由于受到前盖板旋转以及叶轮出口侧壁形状的共同影响，而侧壁对液体流动也存在一定的制约作用，故前腔出口截面压力变化较大；当间隙小于0.2 mm时，前泵腔进口截面和前泵腔轴向中心截面压力沿径向变化不明显；当间隙大于0.2 mm时，前泵腔进口截面和中心截面出现压力沿径向分布呈非对称性，且随着间隙增大，压力不均匀性更加明显，说明前泵腔内液体存在间隙泄漏流动，其主要由剪切流和压差流组成，近似为二维黏性层流运动[5]。

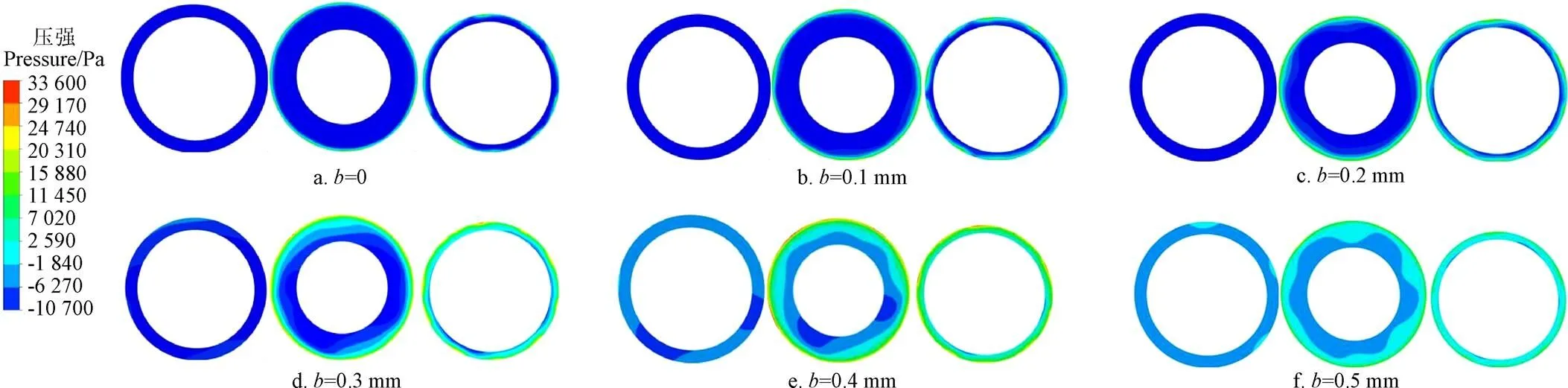
注：b为平衡鼓间隙，mm；图6a中3张图片从左至右分别为1-1截面、2-2截面、3-3截面，下同。

为进一步理清前泵腔压力沿径向分布规律，分别在0.5、和1.5流量下，取首级叶轮前泵腔在相同半径下0、90°、180°和270°处液体的压力平均值，并绘制出压力均值沿径向的变化曲线，如图7所示。由图7可知，首级叶轮前泵腔进口的液体压力呈平衡鼓间隙越大，压力越大的趋势，这是因为平衡鼓间隙较小时，经过平衡管流入吸水室的高压液体较少，因此进入前泵腔液体的压力较小，随着平衡鼓泄漏的高压流体增多，泵腔液体的压力逐渐增大。由于经过密封环间隙进入首级叶轮前腔的无旋液体受到叶轮旋转产生的离心力作用，故不同工况下，前腔内液体的压力呈抛物线型分布规律，这与文献[1]假设泵腔内压力呈抛物线型分布规律结论一致。

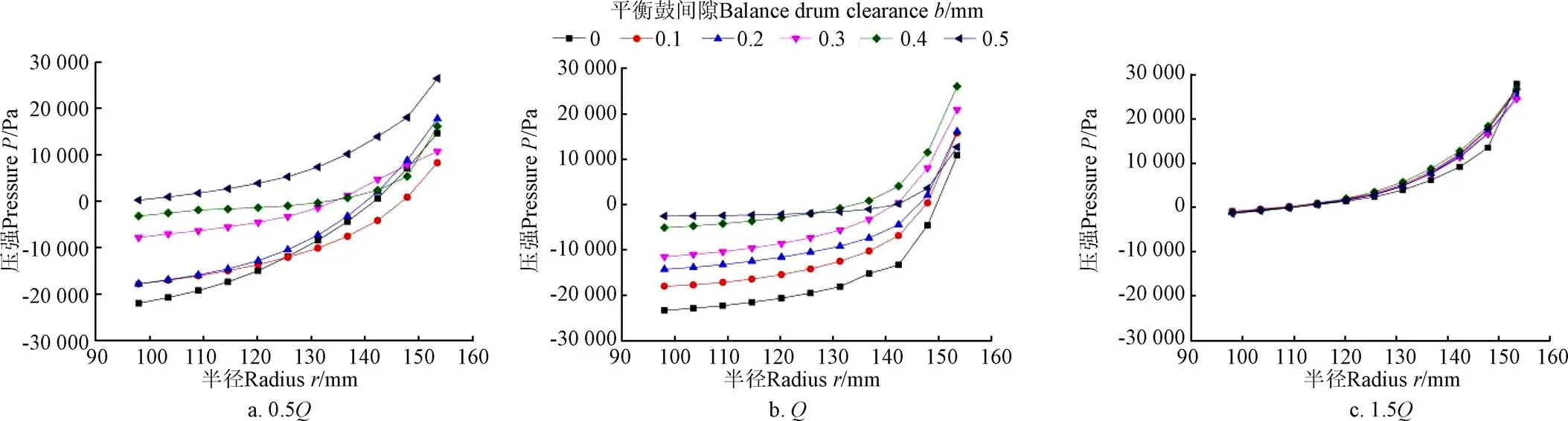
注：Q为设计流量，Q=128 m3·h-1。

由图7还可以看出，不同工况下，首级叶轮前泵腔液体的压力均值沿径向随流量的增大而逐渐减小。在0.5和1.5流量下，不同平衡鼓间隙下的压力增幅无明显规律性，两种工况下，平衡鼓间隙=0.3 mm时压力增幅最小，=0时压力增幅最大，最小增幅分别为最大增幅的50.7%和88.9%。设计流量下，间隙从0～0.4 mm增大时，压力增幅随平衡鼓间隙增大呈逐渐增加趋势，但在间隙0.5 mm时，压力沿径向增幅最小，在间隙为0时压力增幅最大，最小增幅为最大增幅的44.6%，说明随着流入前泵腔内高压流体增多，从叶轮出口向前泵腔回流的液体减少，压力变化减小；当>142 mm时，压力沿径向迅速增大，近似成线性分布，说明此时压力增幅较快，这是因为当接近前泵腔出口处时，泵腔内的液体与叶轮出口处沿径向回流的有旋流体相互碰撞，速度降低较快，故泵腔外径处压力变化较大。

3.2 首级叶轮前腔体流线分布

由于作用在叶轮上的轴向力主要取决于泵腔内部流动状态[3]，基于3.1节进一步分析首级叶轮泵腔内流体的运动形式，选取不同工况下，压力增幅最大和最小的3个平衡鼓间隙=0，0.3，0.5 mm，沿轴向截取首级叶轮前泵腔内的中心截面（=0），得到不同工况下，首级叶轮前泵腔流线图，如图8所示。由图8可知，不同工况下，3种平衡鼓间隙的首级叶轮前盖板内都有一个较大的漩涡区，且漩涡区随着流量的增大逐渐变小，说明该漩涡区是使腔体内压力变化的主要原因。相同工况下，平衡鼓间隙=0时，首级叶轮前泵腔内流线较紊乱，=0.3和0.5 mm时，前腔内流线分布较均匀。

图8 不同工况下首级叶轮前腔流线图

3.3 平衡鼓间隙对轴向力的影响

为了进一步分析平衡鼓间隙与首级叶轮轴向力的关系，通过数值模拟得到不同间隙下多级泵首级叶轮前盖板轴向力1、后盖板轴向力2、轮毂端结构引起的轴向力3、动反力[1]4以及首级叶轮总的轴向力的数值计算结果如表2所示。由表2可知，当平衡鼓间隙由0～0.5 mm增大时，首级叶轮前后盖板的盖板力1和2相比其他因素引起的轴向力取值始终较大，且后盖板力2方向指向叶轮进口，是产生轴向力的主要因素。前盖板力1和轮毂端结构引起的轴向力3随着间隙的增大而逐渐增加，这是因为当平衡鼓间隙增大时，高压流体使吸水室及首级叶轮前盖板压力升高，其值随着间隙增大而逐渐增加。动反力4则受进口速度变化的影响，其值稍有变化但不明显。首级叶轮总的轴向力随着平衡鼓间隙增大，总轴向力呈先减小后增大的趋势，在间隙为0时首级叶轮所受轴向力最大，在间隙为0.3 mm时所受轴向力最小，其最小值为最大值的20.6%，说明平衡鼓可有效减小首级叶轮所受轴向力。

表2 首级叶轮数值计算轴向力结果对比

设计工况下，平衡鼓间隙从0到0.5 mm时，平衡鼓平衡轴向力、11级叶轮总轴向力以及残余轴向力之间的关系如表3所示。由表3可以看出，随着间隙增大，平衡鼓平衡轴向力逐渐减小，这是因为当间隙增大时，末级叶轮后腔与平衡腔压差减小，平衡鼓平衡能力逐渐减弱。11级叶轮总轴向力随着间隙增大呈先减小后增大的趋势，这是因为随着平衡鼓泄漏量的增加，叶轮侧壁间隙内主流流动受到盖板旋转影响减小，轴向力减小，但当泄漏流继续增大时，泵腔内的低压流体与叶轮出口处高压流体碰撞加剧，使压力分布不均，轴向力增大。残余轴向力是指平衡鼓平衡轴向力与11级叶轮总轴向力之差，即止推轴承承受轴向力，残余轴向力随着间隙的增大逐渐增加的。许多文献认为，平衡鼓间隙越小平衡轴向力越大[11-12]；但通过计算发现，当间隙为0.1 mm时，平衡鼓平衡轴向力大于叶轮产生的轴向力，说明平衡鼓平衡轴向力过大；当间隙为0.2 mm时，残余轴向力最小，说明间隙为0.2 mm时平衡鼓轴向力平衡能力最好。

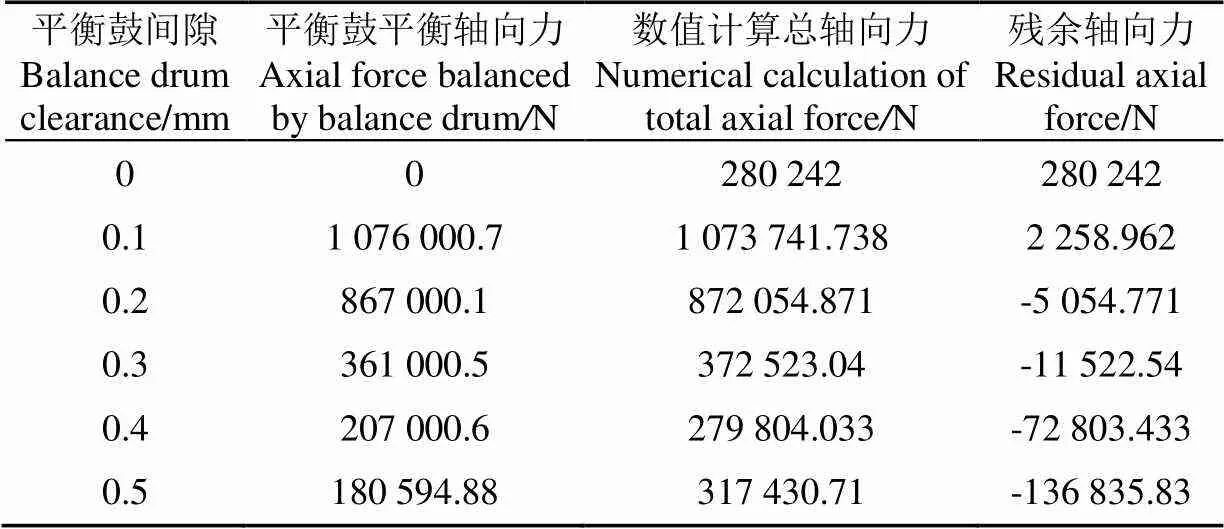
表3 不同平衡鼓间隙平衡轴向力结果对比

为了分析相似多级泵中，不同平衡鼓间隙尺寸对残余轴向力系数的影响，本文引入无量纲化的残余轴向力系数，以及无量纲化的平衡鼓间隙面积（即比面积），即平衡鼓间隙面积与平衡鼓面积的比值，其公式为

平衡鼓间隙0、0.1、0.2、0.3、0.4、0.5 mm，对应的比面积为0、2.2×10-3、4.4×10-3、6.6×10-3、8.8×10-3、11.01×10-3。绘制出=()关系曲线，如图9所示。

注：画圈部分为平衡鼓无法有效平衡轴向力区域。k'为平衡鼓间隙面积与平衡鼓面积的比值，即比面积。

从图9中可以看出，比面积增大时，残余轴向力系数减小；其中，由0增大到2.2×10-3时，降低明显，说明平衡鼓可以有效减小轴向力；当2.2×10-3<<6.6×10-3时，'逐渐由正值变为负值且下降缓慢，说明在此范围内，平衡鼓运行较稳定且可以平衡大部分的叶轮轴向力；当>6.6×10-3时，随着的增大负值降低较快，说明由于平衡鼓前后压差较小，已无法有效平衡轴向力，导致残余轴向力过大，因此在此范围轴承发生断轴的风险较大。

4 结 论

1）设计流量下，首级叶轮前泵腔内液体压力由叶轮前泵腔进口截面至前泵腔出口截面沿轴向压力呈逐渐增大。当平衡鼓间隙小于0.2 mm时，首级叶轮前泵腔体内各截面的压力沿径向分布较均匀，当间隙大于0.2 mm时，各截面内压力沿径向分布呈非对称性，且随着间隙增大，压力不均匀性更加明显。

2）当平衡鼓间隙由0～0.5 mm时，首级叶轮前泵腔中心截面压力值逐渐减小，呈平衡鼓间隙越大，前泵腔压力取值减小趋势。小流量和大流量下平衡鼓间隙为0.3 mm时压力增幅最小，其间隙为0时压力增幅最大，最小增幅分别为最大增幅的50.7%和88.9%；设计流量下，间隙为0.5 mm时，压力沿径向增幅最小，在间隙为0时压力增幅最大，最小增幅为最大增幅的44.6%。

3）不同工况下，首级叶轮前泵腔的漩涡区随着流量的增大逐渐变小，说明该漩涡区是使腔体内压力变化的主要原因。

4）随着间隙增大，11级叶轮所受总轴向力呈先减小后增大的趋势。无量纲化的平衡鼓间隙面积大于6.6×10-3时，平衡鼓无法有效平衡轴向力，该范围轴承发生断裂的风险较大。

[1] 关醒凡. 现代泵理论与设计[M]. 北京：中国宇航出版社，2011：498－530.

[2] 金建波. 平衡鼓平衡轴向力方法的研究与探讨[D]. 杭州：浙江工业大学，2010.

Jin Jianbo. Study and Investigation on the Axial Force Balance Method by Balance Drum[D]. Hangzhou: Zhejiang University of Technology, 2012. (in Chinese with English abstract)

[3] Johann Friedrich Gülich. Centrifugal Pumps[M]. Switzerland：Springer- Verlag Berlin Heidelberg 2008, 2010: 544－545.

[4] 刘在伦，董玮，张楠，等. 离心泵平衡腔液体压力的计算与验证[J]. 农业工程学报，2013，29(20)：54－59.

Liu Zailun, Dong Wei, Zhang Nan, et al. Calculation and validation of fluid pressure of balance cavity in Centrifugal Pump[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(20): 54－59. (in Chinese with English abstract)

[5] 董玮，楚武利. 离心泵叶轮平衡腔内液体流动特性及圆盘损失分析[J]. 农业机械学报，2016，47(7)：29－35.

Dong Wei, Chu Wuli. Analysis of flow Characteristics and disc friction loss in balance cavity of centrifugal pump impeller[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016，47(7)：29－35.(in Chinese with English abstract)

[6] Dong Wei,Chu Wuli. Numerical investigation of the fluid flow characteristic in the hub plate crown of a centrifugal pump[J]. Chinese Journal of Mechanical Engineering, 2018, 31(1): 64.

[7] Dong Wei, Chu Wuli. Numerical investigation of fluid flow mechanism in the back shroud cavity of a centrifugal pump[J]. Journal of Applied Fluid Mechanics, 2018, 11(3): 709－719.

[8] 董玮，楚武利. 离心泵后泵腔内液体压力数值分析与验证[J]. 机械工程学报，2016，52(4)：165－170.

Dong Wei, Chu Wuli. Numerical analysis and validation of fluid pressure in the back chamber of centrifugal pump[J].Journal of Mechanical Engineering, 2016, 52(4): 165－170. (in Chinese with English abstract)

[9] Gordon Kirk, Rui Gao. Influence of preswirl on rotordynamic characteristics of labyrinth seals[J]. Tribology Transactions, 2012, 55: 357－364.

[10] Rui Gao, Gordon Kirk. CFD study on stepped and drum balance labyrinth seal[J]. Tribology Transactions, 2013, 56: 663－671.

[11] 张贤安，金建波. 平衡鼓间隙尺寸对多级泵轴向平衡能力影响的分析[J]. 流体机械，2013(41)：49－53.

Zhang Xianan, Jin Jianbo. Analysis on the influence of balance drum gap sizes on axial balanced capacity in multistage pumps[J]. Fluid Machinery, 2013(41): 49－53. (in Chinese with English abstract)

[12] 林玲. 平衡鼓间隙对离心泵轴向力平衡的影响[J]. 轻工机械，2013(6)：13－16.

Lin Ling. Effect of balance drum clearance on axial force balance of multistage centrifugal pumps[J]. Light Industry Machinery, 2013(6): 13－16. (in Chinese with English abstract)

[13] 张翼飞，杨从新. 平衡鼓直径的实验确定法[J]. 水泵技术，1996(5)：24－27.

Zhang Yifei, Yang Congxin. Method for determining balanced diameter of multistage pump[J]. Pump Technology, 1996(5): 24－27. (in Chinese with English abstract)

[14] 欧阳武，袁小阳，宋建军，等. 平衡鼓和平衡盘的系统模型及应用[J]. 机械科学与技术，2012，31(11)：1731－1734.

Ouyang Wu, Yuan Xiaoyang, Song Jianjun, et al. System modeland application of balancing drum and balancing disc[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(11): 1731－1734. (in Chinese with English abstract)

[15] 汪建华，戴静君. 平衡鼓和平衡盘联合结构的优化设计[J].汉江石油学院学报，2000，22(2)：52－54.

Wang Jianhua, Dai Jingjun. Optimum design of the joint structure of balance drum and balance disk[J]. Journal of Hanjiang Petroleum Institute, 2000, 22(2): 52－54. (in Chinese with English abstract)

[16] 汪建华，周志宏，赵子传. 注水泵双平衡鼓装置的优化设计[J]. 石油机械，2000，28(8)：8－11.

Wang Jianhua, Zhou Zhihong,Zhao Zizhuan. Optimum design of double balance drum device for water injection pump[J]. Petroleum Machinery, 2000, 28(8): 8－11. (in Chinese with English abstract)

[17] 陆河权，牟介刚，郑水华，等. 凹槽深度对新型平衡鼓性能影响的研究[J]. 浙江工业大学学报，2012，40(5)：559－566.

Lu Hequan, Mu Jiegang, Zheng Shuihua, et al. Study on the influence of the depth of groove on the performance of novel balance drum[J]. Journal of Zhejiang University of Technology, 2012, 40(5)：559－566. (in Chinese with English abstract)

[18] 陈云富. 离心泵泵腔内压力分布规律的研究[D]. 兰州：兰州理工大学，2005.

Chen Yunfu. The Research of Pressure Distribution Rule in the Chamber of Centrifugal Pump[D]. Lanzhou: Lanzhou University of Technology, 2005. (in Chinese with English abstract)

[19] 张春晋，孙西欢，李永业，等. 螺旋流起旋器内部流场水力特性数值模拟与验证[J]. 农业工程学报，2018，34(1)：53－62.

Zhang Chunjin, Sun Xihuan, Li Yongye, et al. Numerical simulation and verification of hydraulic characteristics of internal flow filed in spiral flow generator[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(1): 53－62. (in Chinese with English abstract)

[20] 李伟，季磊磊，施卫东，等. 基于Hilbert-Huang变换的混流泵流动诱导振动试验[J]. 农业工程学报，2018，34(2)：47－54.

Li Wei, Ji Leilei, Shi Weidong, et al. Experiment of flow induced vibration of mixed-flow pump based on Hilbert-Huang transform[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(2): 47－54. (in Chinese with English abstract)

[21] 李伟，施卫东，蒋小平，等. 多级离心泵轴向力的数值计算与试验研究[J]. 农业工程学报，2012，28(23)：52－59.

Li Wei, Shi Weidong, Jiang Xiaoping, et al. Numerical calculation and experimental study of axial force on multistage centrifugal pump[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(23): 52－59. (in Chinese with English abstract)

[22] Cao Weidong,Dai Xun,Hu Qixiang.Effect of impeller reflux balance holes on pressure and axial force of centrifugal pump[J]. Journal of Central South University, 2015, 22: 1695－1706.

[23] Wang Chuan, Shi Weidong, Li Zhang. Calculation formula optimization and effect of ring clearance on axial force of multistage pump[J]. Mathematical Problems in Engineering. DOI:10.1155/2013/749375.

[24] Zhou L, Shi W, Li W, et al. Numerical and experimental study of axial force and hydraulic performance in a deep-well centrifugal pump with different impeller rear shroud radius[J]. Journal of Fluid Engineering, 2013, 135(10): 104501-1－104501-8.

[25] BjÖrnW,Friedrich B,Hans D. Investigation of the flow in the impeller side clearances of a centrifugal pump with volute casing[J]. Journal of Thermal Science, 2012, 2(3): 197－208.

[26] Yogesh J. Shear and preeure driven flow and thermal transport in microchannels[C]//Proceedings of the Sixth International ASME Conference on Nanochannels, Microchannels and Minichannels (ICNMM2008). Darmstadt, Germany, 2008: 1677－1688.

Influence of balance drum clearance on pressure of front cavity of first stage impeller and axial force of multistage pump

Qian Chen, Yang Congxin, Fu You, Zhang Yang, Hou Kaiwen

(,730050,)

The ability of the balance drum to balance the axial force is the key factor for the failure of multistage centrifugal pump. However, during the operation of the balance drum, due to the long-term collision with the liquid or the friction with the casing, the leakage amount at the balance drum clearance is gradually increased, resulting in the balance drum being worn. Therefore, studying the leakage flow is critical to the ability of the balance drum to accurately balance the axial force of the entire impeller. In this paper, three-dimensional turbulent flow of multistage centrifugal pump was simulated by using the CFD code FLUENT. Besides, steady simulation was conducted for different operating points of the pump, the turbulence was simulated with shear stress transportation(SST) turbulence model together with automatic near wall treatment. CFD results were compared with those from the model test. And the results of the pressure and leakage in the balance pipe and the external characteristics of the multistage pump were basically consistent with the experimental results. Moreover, the maximum errors of head, efficiency and shaft power were 4.17%, 2.81% and 4.25% respectively, but the experimental flow rate of balance pipe was always greater than the simulated one. This was mainly because the influence of orifice flowmeter in the pipe had been not taken into account in the numerical simulation. The maximum error of the flow rate of the balanced pipe at the design point was 4.49%. The maximum error of pressure was 2.5%. It showed that the calculation method selected in this paper could provide a reliable guarantee for this study. The results showed that at the design flow rate, the liquid pressure in the front cavity of the first impeller increased gradually along the axial direction from the inlet section to the outlet section. When the balance drum clearance was less than 0.2 mm, the pressure distribution along the radial direction was uniform in each section. But when the clearance was more than 0.2 mm, it was asymmetric. Furthermore, with the increase of clearance, the pressure inhomogeneity became more obvious. Moreover, at 0.5(is design flow,=128 m3/h) and 1.5flow rates, there was no obvious regularity of pressure increment along the radial direction under different clearances. The pressure increment was the smallest when the balance drum clearance was 0.3 mm, and the biggest when the balance drum clearance was 0. And under the above 2 conditions, the minimum increments were 50.7% and 88.9% of the maximum, respectively. When the clearance increased from 0 to 0.5 mm, under design flow rate, the pressure increased gradually along the radial direction. Wherein, when the clearance was 0 and 0.5 mm, the pressure increment was the maximum value and the minimum value, respectively, and the minimum value was 44.6% of the maximum value. Besides, there was a large vortex region in the front cavity of the first impeller, when the clearance of balance drums was 0, 0.3 and 0.5 mm, respectively. The vortex region decreased gradually with the increase of flow rate, which indicated that the appearance of the vortex region was the main reason for the change of pressure in the cavity. In addition, with the increase of clearance, the total axial force of 11 stage impellers decreased first and then increased. And when non-dimensionalized balance drum clearance area was greater than 6.6×10-3, the balance drum could not effectively balance the axial force. Furthermore, the bearing had a greater risk of fracture in this range. This research can provide useful reference for design of balance drum and prediction of risk of bearing fracture.

pumps; pressure; numerical calculation; front cavity of first stage impeller; balance drum clearance; axial force

10.11975/j.issn.1002-6819.2019.02.005

TH311

A

1002-6819(2019)-02-0033-07

2018-07-16

2018-12-30

甘肃省自然科学基金资助项目（061707）；兰州市人才创新创业项（2015-RC-29）

钱 晨，讲师，研究方向为多级泵泵腔流动机理的研究。Emai：495980912@qq.com

钱 晨，杨从新，富 友，张 扬，侯凯文. 平衡鼓间隙对首级叶轮前泵腔压力及多级泵轴向力的影响[J]. 农业工程学报，2019，35(2)：33－39. doi：10.11975/j.issn.1002-6819.2019.02.005 http://www.tcsae.org

Qian Chen, Yang Congxin, Fu You, Zhang Yang, Hou Kaiwen. Influence of balance drum clearance on pressure of front cavity of first stage impeller and axial force of multistage pump[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(2): 33－39. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.02.005 http://www.tcsae.org