成品油中转油库选址问题研究

（北京物资学院 信息学院，北京 101149）

1 引言

成品油配送分为一次配送和二次配送，一次配送是成品油从炼油厂运输到中转油库的过程；二次配送指成品油从中转油库运到加油站或最终用户的过程。中转油库是连接成品油一次配送和二次配送的重要环节。中转油库选址位置直接影响成品油一次配送和二次配送的物流成本。

针对中转油库选址问题已有部分学者开展了研究工作。辜勇等利用重心法研究了单个和多个油库选址问题[1]；杜乐乐等利用最大覆盖模型研究了拟建造油库数量有限情况下的选址问题[2]；姜玉梅等基于安全环保角度对拟建油库的选址和设计进行了研究[3]；吴勤旻等构建了一个二层优化模型，针对油库建设成本和二次运输成本提出了确定理想选址区域和可行点的相关方法[4]；米晓芳等研究了考虑碳成本的油库选址问题[5]；李横等[6]和张卫明等[7]结合军用油库的特殊性，分别研究了基于遗传算法和基于改进粒子群算法的军用油库选址优化问题。以上研究大部分以成品油二次配送成本极小化为主要目标，很少同时考虑成品油一次配送和二次配送总成本，而且以上研究都是从已有的油库备选点中选择油库位置，文献中尚未发现关于不考虑备选点情况下的油库选址问题的研究结果。由于实际进行油库选址时可能并没有现成的油库备选点，因此有必要在没有油库备选点的前提下综合考虑成品油一次配送和二次配送成本，研究成品油中转油库选址问题。

本文将在没有油库备选点的情况下，同时考虑成品油一次配送和二次配送成本，以拟建油库位置坐标为决策变量、成品油一次配送和二次配送成本和油库运行成本之和极小化为目标，建立成品油中转油库选址问题的混合整数规划模型，并设计求解模型的两阶段算法，寻求中转油库的最佳位置。

2 成品油中转油库选址问题的数学模型

成品油中转油库选址问题可以描述为：在某一地区有一座炼油厂（序号为0），n个加油站（序号分别为1,2,…,n）。已知炼油厂的位置坐标为(a0,b0)，加油站j的位置坐标为(aj,bj)，加油站j的需求量为qj,为了建立成品油配送网络，拟在该区域内最多建立m个中转油库。第i个中转油库建设费用为ci，最大容量为Pi，已知从炼油厂到中转油库的单位运输费为e（元/t·km）, 从中转油库到加油站的单位运输费为h（元/t·km）。问如何选择中转油库位置，才能使成品油一次配送和二次配送成本以及中转油库建设成本之和最低？

为了建立数学模型，定义如下决策变量：

(xi,yi)：第i个中转油库的位置坐标；

fij：从中转油库i运往加油站j的成品油数量；

ri：从炼油厂运往中转油库i的成品油数量。

成品油中转油库选址问题可以表示成如下混合整数非线性规划模型:

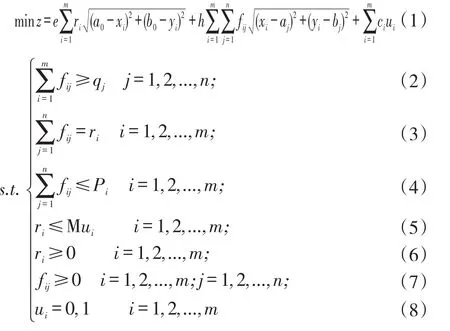
目标函数（1）表示极小化成品油一次配送和二次配送成本以及油库建设成本之和；约束条件（2）表示满足各个加油站的需求量；约束条件（3）为中转油库流量平衡约束；约束条件（4）表示从中转油库运往各个加油站的成品油之和不超过其最大容量限制；约束条件（5）表示中转油库的建立条件；约束条件（6）-（8）表示变量取值约束。

3 算法设计

成品油中转油库选址问题的数学模型是一个混合整数非线性规划模型，对于小规模问题可以直接利用Lingo软件编程求解，对于大规模问题直接求解混合整数非线性规划运行时间太长，因此需要设计求解模型的快速有效算法。本节将根据成品油中转油库选址问题数学模型的特点，设计求解问题的两阶段算法。

第一阶段：确定拟建立的中转油库个数并根据加油站的位置和需求量将加油站进行分组，使得每组加油站恰好由一个中转油库提供配送服务。第二阶段：根据炼油厂和每组加油站的信息，确定每个中转油库的位置坐标。

3.1 第一阶段的算法步骤

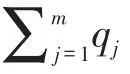
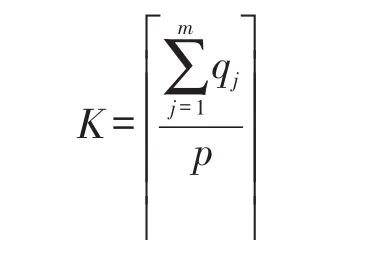
第2步：随机选择K个加油站作为分组的中心点，确定每个分组拟建立的中转油库容量。

第3步：计算每个加油站到各个中心点的距离，在考虑中转油库容量限制的前提下按照加油站到中心点的距离由近到远将各个加油站划分到一个最佳的分组中。方法是：对于每一个加油站，首先选择离其最近的分组，判断将加油站加入该分组以后，分组中加油站的总需求量是否超过油库最大容量限制，如果不超过，则将加油站加入该分组，否则考虑下一个分组，直到选择出一个合适的分组为止。

第4步：根据分组以后的结果，计算每组加油站对应的重心点坐标。将每组加油站对应的重心点作为新的中心点，转第3步。

重复第3、4步，直到分组结果稳定或迭代次数达到预先设定的最大值。

3.2 第二阶段的算法

经过第一阶段分组之后，每组加油站恰好被划分到一个分组中，每组加油站恰好可以由一个中转油库提供服务。由于每组中包含的加油站位置坐标、需求量、炼油厂位置坐标等信息均已知，确定各组加油站对应的中转油库最佳位置的问题可以表示成一个无约束优化问题。

假设第k组包含的加油站序号集合为Gk，则第k组加油站的总需求量为，为该组加油站提供服务的中转油库最佳位置(xk,yk)是下列无约束优化问题的最优解：

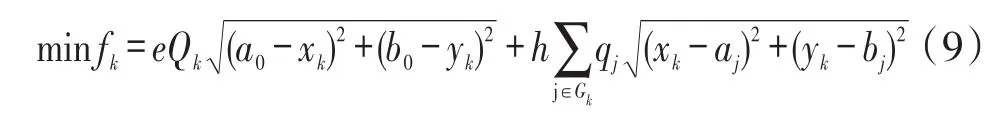
其中第一项表示从炼油厂到中转油库的总运费，第二项表示中转油库到该组中各个加油站的总运费。

该模型可以直接利用Matlab优化工具箱中的fminunc函数求解。其调用格式为[x,fval,exitflag,output]=fminunc('fun',x0,options)；其中fval是返回目标函数在最优解x点的函数值，x0是初始参数，exitfalg是返回算法的终止标志，fun是目标函数,options设置优化选项参数。

4 算例分析

4.1 小规模算例

某地区有一个炼油厂（序号为0）和12个加油站（序号为1-12），炼油厂和加油站的位置坐标及需求量见表1。各个油库的最大容量均为40t，每个油库建设费用为13万元，从炼油厂到中转油库的单位运输费用为30元/t·km，从中转油库到加油站的单位运输费用为50元/t·km。试确定该地区的中转油库位置使得成品油配送总成本最低。

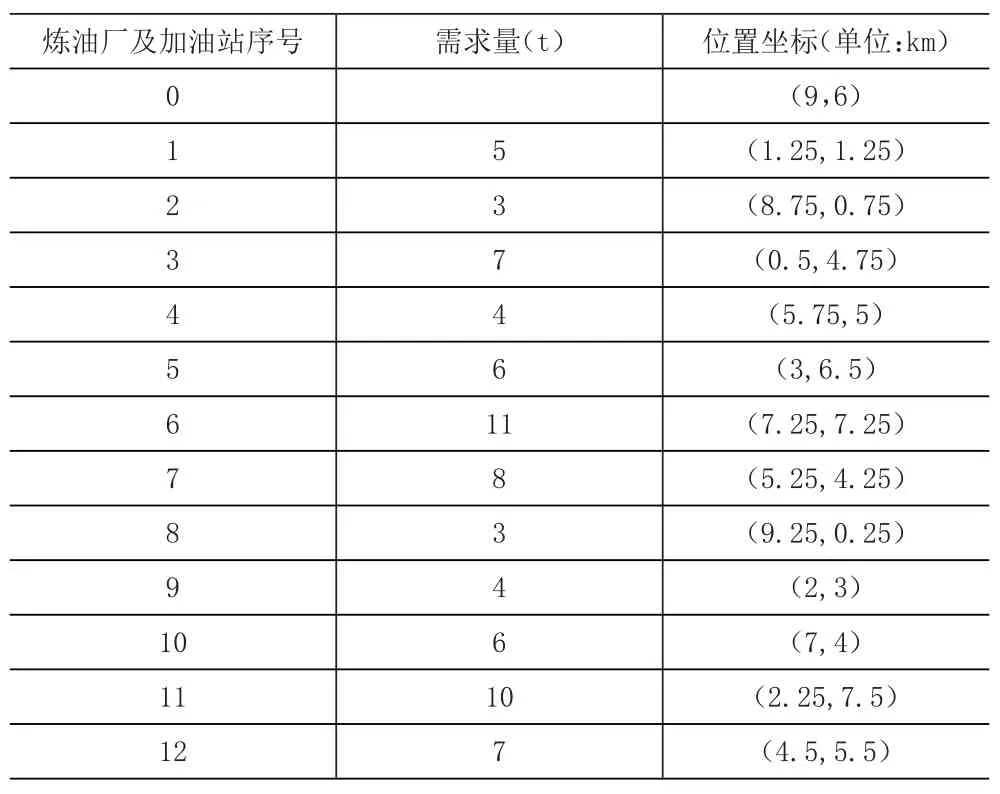
表1 炼油厂及加油站位置坐标和需求量

（1）利用Lingo软件求解混合整数规划模型得到精确最优解。首先利用Lingo11.0软件编程求解混合整数规划模型，程序运行100h仍未结束，手动终止程序，记录程序运行得到的局部最优解为：一共需要建立两个油库，两个油库的位置分别为（8.279 1，5.765 4）和（4.5，5.5），两个油库服务的加油站总需求量分别为34t，40t。建设两个油库及成品油一、二次配送费用总和为277 199.6元。各个油库位置及服务的加油站序号见表2，其中加油站4同时由两个油库提供服务。

表2 油库位置及服务的加油站序号

（2）利用两阶段算法求近似最优解。利用两阶段算法求解本例，用matlab编程，在AMD A10-8700P Radeon R6，10 Compute Cores 4C+6G 1.80GHz处理器上运行，经过0.585s，得到问题的近似最优解：共需要建立2个油库，两个油库的位置坐标分别为：（4.5，5.5），（6.231 1，7.725 5）；油库建设成本和一次配送、二次配送总成本为277 067.754 9元。各个油库服务的加油站序号见表3。

表3 各个油库服务的加油站序号

比较两种算法的计算结果可以看出，一方面，lingo程序求解混合整数规划模型无法在短时间内得到全局最优解，经过100h运算得到的仍然是局部最优解，两阶段算法的总运行时间不足1s，因此两阶段算法具有明显的计算时间优势；另一方面，两阶段算法得到的近似最优解总费用比lingo程序运算100h得到的局部最优解更好，其目标函数值减少了131.845 1元，因此，两阶段算法的计算效果也明显优于直接求解混合整数规划模型的结果，因此两阶段算法适合大规模问题的求解。

4.2 大规模算例

根据北京地区100个加油站的位置信息构造大规模算例验证模型和算法的有效性。100个加油站位置分布情况如图1所示，各个加油站的需求量取5-20（t）的随机数，炼油厂坐标为（116.6,40.2），假设每个油库的建设费用均为20万元，拟建的中转油库最大容量均为260t，从炼油厂到中转油库的单位运输费用为40元/t·km，从中转油库到加油站运输费用为60元/t·km。

根据以上数据，利用两阶段算法求解，程序运行0.74s得到近似最优解，该地区需要建设5个中转油库为加油站提供服务，油库建设成本及一、二次配送成本之和为1 021 333.65元，油库位置及服务加油站的情况见表4和图1。由同一个中转油库服务的加油站用相同的图形表示在图1中，其中实心图形表示中转油库，对应空心图形表示油库所服务的加油站。从图1可以看出，由同一个中转油库服务的加油站位置较为集中，该结果与北京地区实际中转油库及加油站的分组情况大体一致。

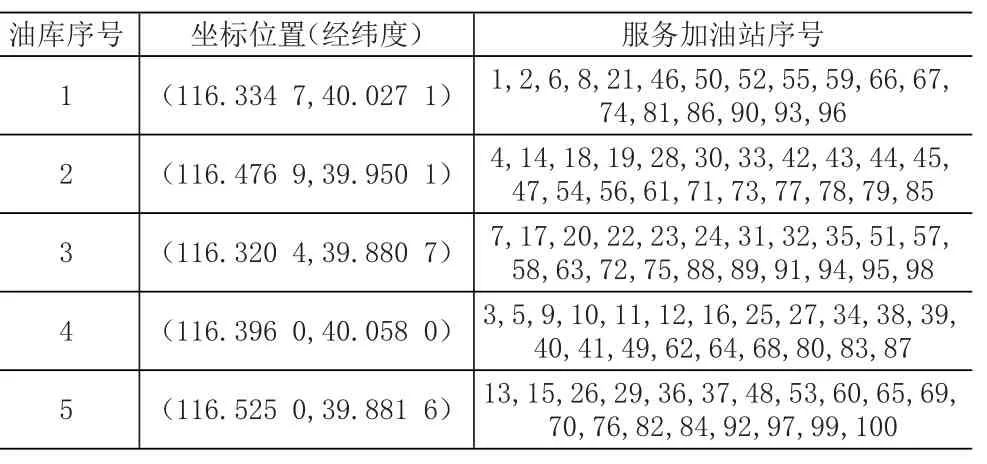
表4 油库位置及服务的加油站序号

图1 北京地区5个中转油库的选址位置及服务的加油站情况

5 结语

本文研究了中转油库选址问题，综合考虑了成品油一次配送、二次配送成本以及中转油库建设成本，以中转油库位置坐标为决策变量、总成本极小化为目标函数，建立了混合整数规划模型，并设计了求解模型的两阶段算法。利用具体算例验证了模型和算法的有效性，模拟计算结果显示，对于小规模问题，运行两阶段算法不足1s就可以得到近似最优解，其目标函数值优于用lingo软件直接求解混合整数规划模型运行100h得到的局部最优解。对于包含100个加油站的大规模算例，两阶段算法仍然可以在短时间内得到近似最优解。

本文研究中，仅考虑了一个炼油厂的情况，且没有考虑炼油厂到中转油库的道路运输能力限制，实际中可能有多个炼油厂，炼油厂到中转油库的道路运输能力可能有限制，而且在不同位置建立中转油库的建设成本也会有较大的差别，后续研究中我们将考虑多个炼油厂、道路运输能力限制以及油库建设成本与地理位置关系等因素，建立不同场景下的中转油库选址问题的数学模型，并设计求解模型的算法，为解决实际问题提供决策依据。