新型磁流变阻尼器的仿真方法研究
2019-02-25李勇涛郑建国
李勇涛,郑建国
(南京理工大学 机械工程学院, 南京 210094)
磁流变阻尼器(MRD,即Magnetorheological Damper)具有一般减振器件所没有的阻力可控性能,利用流体在磁场作用下的流变特性,对冲击载荷具有良好的控制缓冲效果[1]。磁流变的种类颇多,对应的粘度模型也不尽相同。除了在不同的磁场下表现出不同的屈服应力,在不同的剪切速率下,粘度也可能发生较大改变。在磁流变阻尼器中,流体在间隙处不同的位置也会受到不同的磁化强度[2]。而应用于火炮反后坐的MRD,都具有很高的速度,用常见的动网格模拟方法又很难保证精度。基于以上五点,这给应用于武器反后坐的MRD数值模拟带来很大的困难。对于MRD的仿真研究,大多都以静态局部压力模拟和耦合场模拟为主。耦合场难以明确粘度模型也难以构造模型的动力学模型,而静态模拟阻尼器实际工况也不是各个时刻的静态叠加[3]。到目前为止,还没有一个准确的理论描述磁流变效应,因此在FLUENT(一款流体仿真软件)单纯地导入材料特性并不能准确模拟实际流场的状态[4]。
针对以上问题,作者首先在ANSYS中建立阻尼器活塞模型并对其磁场仿真,得不同区域的BSUM(总磁通密度值),然后利用ICEM-CFD建立其内部全流场计算模型,进而在FLUENT进行瞬态模拟,通过UDF(用户自定义函数)和基于区域整体运动的方法将拟合出的有关I与τy的式子导入不同的区域参与计算,从而较为精确的仿真出阻尼器工作时不同时刻的内部流场状态。
1 新型磁流变阻尼器结构
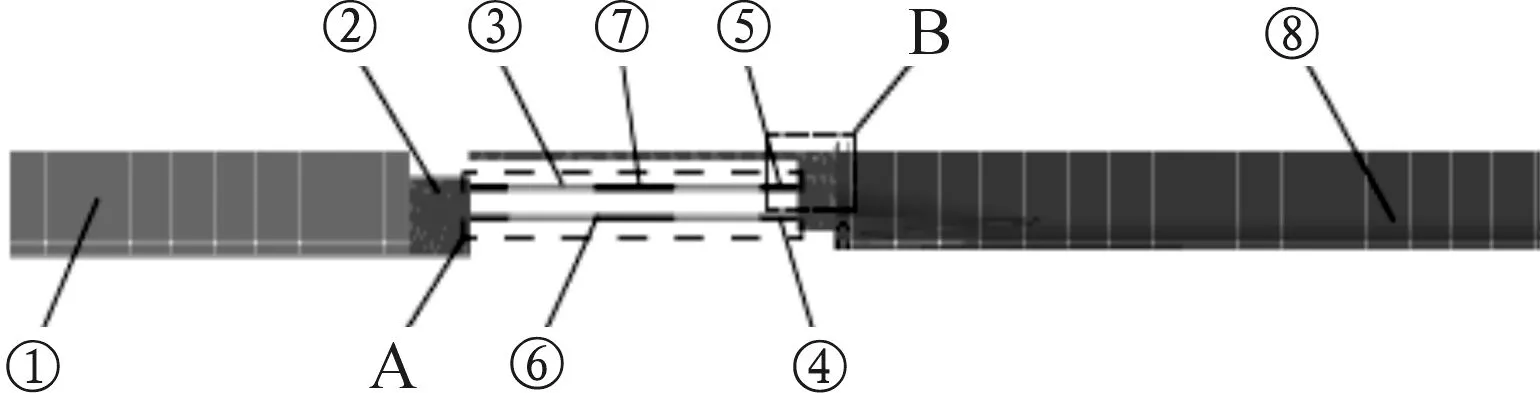
研究对象是双杆双通道式阻尼器,其共有4组线圈,轴向两线圈电流方向相反,横向相同。结构示意图如图1。

1.外壳;2.第1层筒;3.第2层筒;4.第3层筒; 5.固定装置;6.线圈;7.内阻尼间隙;8.外阻尼间隙;9.轴
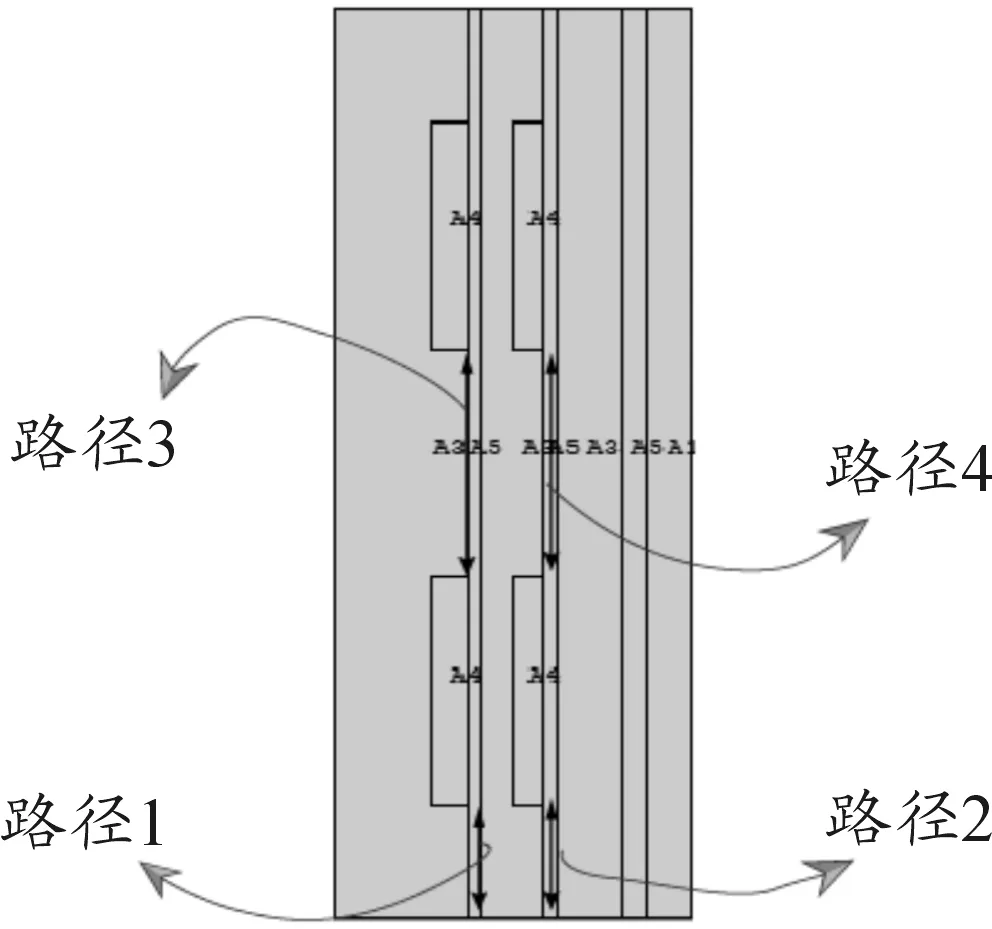
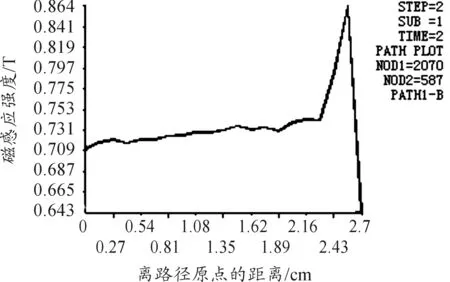
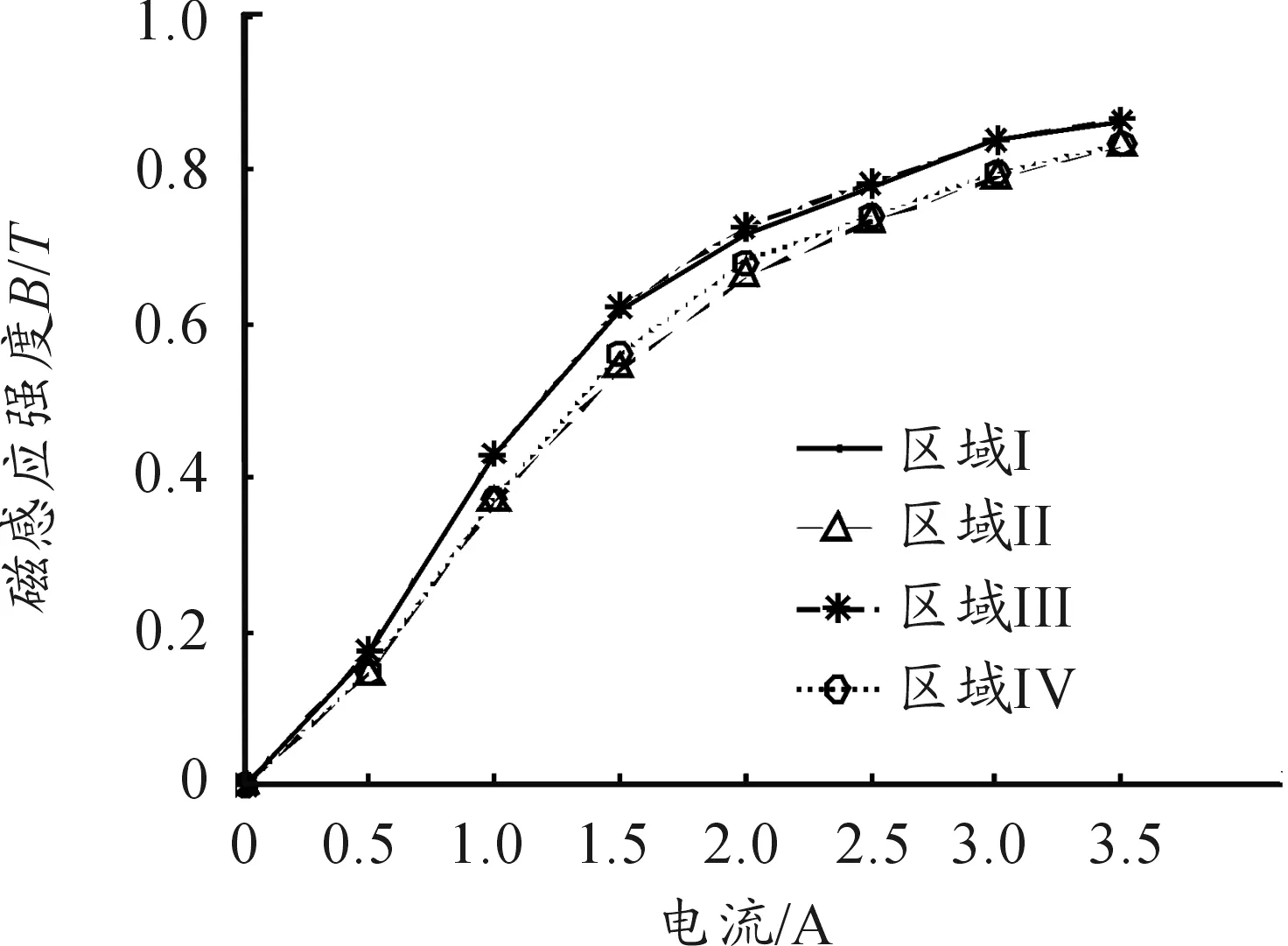
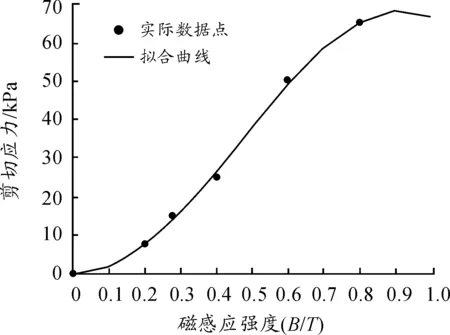
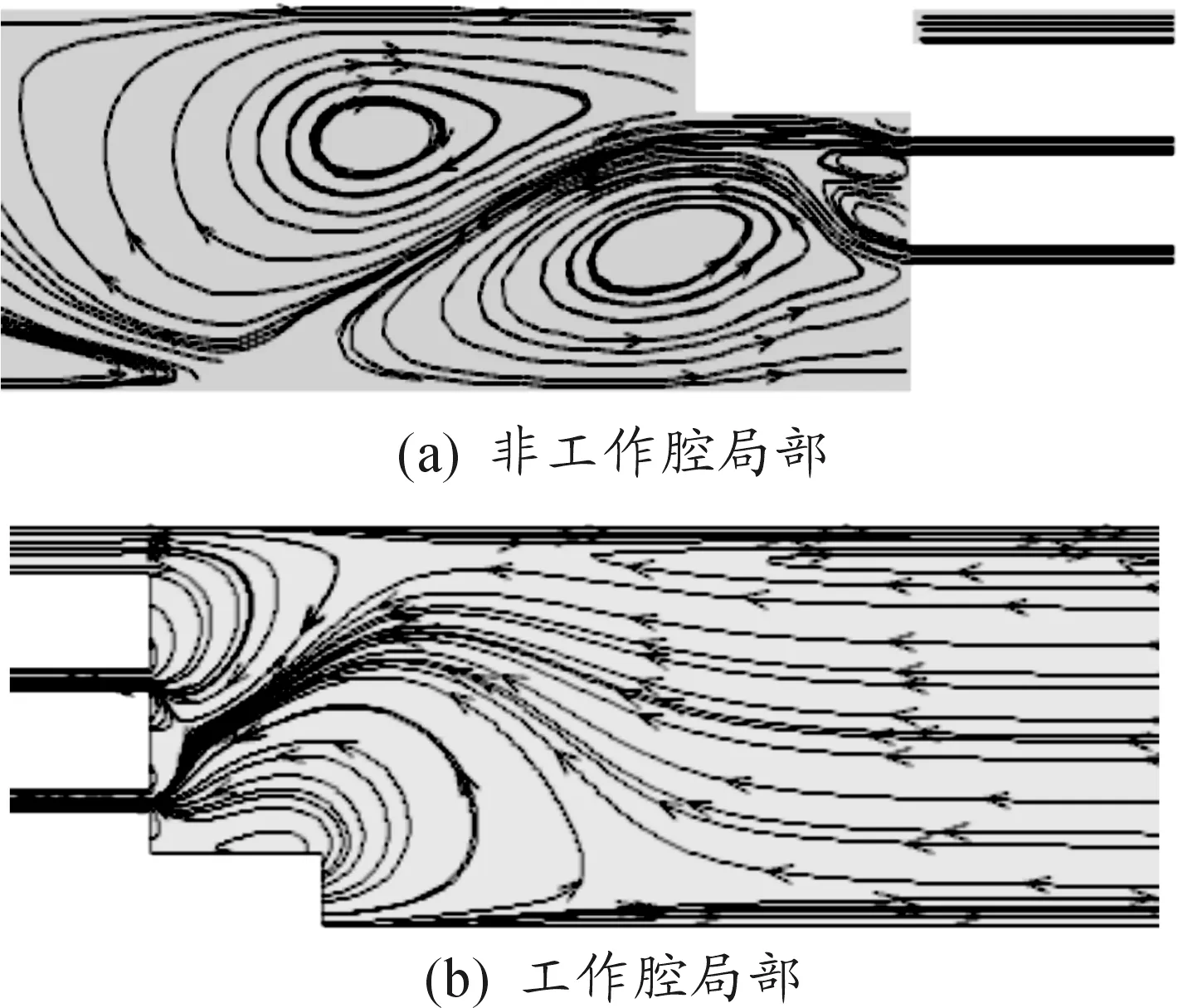
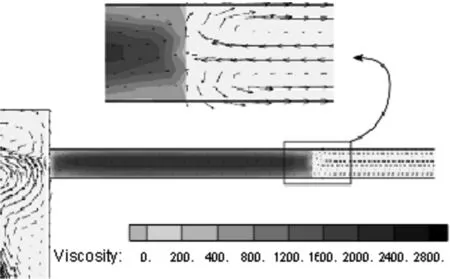
磁流变效应是指体在场作用下,流体的表观 黏度发生了巨大的变化, 甚至在磁场强度达到某一临界值时,流体停止动而固化并具有定的抗剪切。磁流变效应作为一种殊物理材料,还表现出固体所特有的屈服现象。采用MRF-132LD磁流变液,由于后坐MRD比普通的MRD经历更大的速度,粘度模型选用Herschel-Bukley模型[5]。图2为H-B和bingham剪切屈服应力和剪切速率的关系。0 图2 两种模型的曲线 在ANSYS中建模并仿真,按照穿过阻尼通道磁感应强度的分布,分为4个区域,在其中分别定义路径,如图3所示。沿着路径对磁感应强度积分,最终将积分后的值除以路径长度,得出均值。分别模拟电流为0.5 A、1 A、1.5 A、2 A、2.5 A、3 A、3.5 A时的情况。 图3 区域中定义的路径 图4为2 A电流下路径一的磁感应强度分布曲线,图5为此电流下的云图。图6表示不同的电流下,通道各区域的磁感应强度大小。 图4 路径1磁感应强度分布曲线 图5 磁感应强度分布云图 图6 不同电流下激活区各区域磁感应强度模拟结果分析 1) 从图4可见,除个别点外,同一区域磁感应强度分布均匀差距在0.03T之间,做平均处理比较合理。 2) 从图6可见,区域Ⅰ与区域Ⅲ、区域Ⅱ与区Ⅳ的BSUM值相近,将其视为内外两大区域。内阻尼通道率先有饱和的趋势,外阻尼通道随后。在MATLAB中拟合得到B-I关系: B1=-0.001 3I3-0.070 9I2+0.513 7I-0.020 8 (1) B2=-0.006 3I3-0.028I2+0.414 4I-0.016 7 (2) 对活塞两侧腔室上(不包括活塞及其周围区域)部分划分四边形结构化网格为运动变形区。采用三角形非结构化网格对剩余部分划分,此部分为运动非变形区[7]。根据磁场强度分布不同将两个通道划分为10个部分,区域内部边界类型为interior[8]。活塞周围不适合网格光顺或者重构,但是活塞附近一部分关键流动区域在整个运动过程中,形状并未发生变化。令这部分区域作整体运动,将变形区域移到阻尼器两端较为规则的边界区域。后坐时,网格在左端边界生成,在右端边界消亡。该方法最重要特点是要让间隙处的网格随活塞一起运动,这样就方便UDF对流体进行定义,使不同时刻流经通道的流体在激活的对应位置赋予不同的粘度属性。 根据区域状态的不同共分为8个部分,分别合理设置这些区域的网格。共91 218个网格,最小网格高度0.2 mm,最小正交质量为0.55。如图7所示为其整体网格图,图8为通道部分局部网格图,图9为活塞附近区域网格图。 1.运动变形区Ⅰ;2.运动非变形区;3.非激活区;4.激活区Ⅰ;5.激活区Ⅱ;6.激活区Ⅲ;7.激活区Ⅳ8.运动变形区Ⅱ 图8 A通道局部网格图 图9 B区域局部网格图 在PROFILE文件指定运动速度,用插值的方法生成数据驱动边界。通常这一速度应由冲击载荷由理论计算转化产生,但为了避免带来计算误差,这里通过实测火炮后坐速度产生。动网格采用铺层法,分裂率为0.4,合并率设为0.1。 FLUENT中H-B模型粘度公式 (3) (4) 根据该型磁流变液的数据,采用多项式拟合其屈服应力和磁感应强度的关系,如图10所示为其拟合效果图,拟合得到: τy=-1.866 06e5B3+2.611 22e5B2-8.162e3B (5) 图10 拟合MRF的τy-B曲线 仿真初始温度为15 ℃,采用couple求解器,2D轴对称模型。湍流模型选用RNGk-ε模型,由于阻尼器内部压力急剧变化,压力项选用PRESTO!的插值方法。为了提高模拟的准确度,动量方程采用二阶迎风格式离散。时间步长为1×10-5s。 分别仿真出不同电流下阻尼器内部的工作状态,在Tecplot中分析处理数据,以下数据均为1A时刻。图11为不同时刻活塞附近流体的压力分布云图,0.026 s为速度最大时刻。图12为0.026 s最大速度时刻两个腔室的流线图,图13为0.036 s时刻流体的粘度图。图14位后坐结束时刻速度矢量和粘度云图。 图11 不同时刻部分局部流体压力云图 图12 0.026 s时刻流线图 图13 0.036 s的区域三四附近流体的粘度云图 图14 0.17 s后坐结束时刻速度矢量图和粘度云图 为了进一步验证模型的准确性,取阻尼器压力腔的一点P进行压力测试,如图15。以某小型火炮为实验装备进行小射角(θ<15°)射击实验,并与模拟结果进行了对比,如图17所示。选用压电式压力传感器Y1001型,灵敏度为0.1 pC/KPa,量程为0~30 MPa,非线性小于1%FS,如图16为其传感器安装位置。 图15 压力腔中取点的位置 图16 压力腔压力传感器的安装 图17 压力腔模拟结果与实验数据曲线 1) 图11所示不同时刻部分局部流体压力云图表明,后坐时远离活塞区的流体压力分布比较均匀,非工作腔始终处于低压状态,活塞运动对附近流体产生“吸引”作用,AP1周围出现负压区域,随流动时间的增加而增加。在阻尼通道AP3有较大的压力梯度,且出口出现负压。工作腔压力分布比较均匀。 2) 从图12(a)所示的流线图表明,由于阻尼通道强烈的节流作用,流道内压力下降而流速急剧上升,在出口处形成淹没射流。两股射流碰撞、交汇,由于引射作用,形成漩涡。流动类似于高雷诺数的二维后向台阶流,可以看出在两个较大台阶附近均形成漩涡,漩涡中心形成负压。除此之外在阻尼通道附近还有3个小漩涡。从图12(b) 所示的流线图表明,在工作腔靠近间隙的流体流线弯曲,说明流动变化较大而远离活塞的地方流线分布均匀,近似于层流。 3) 由图13所示的粘度云图可知,在被磁化的区域,远离阻尼通道中心线的流体磁流变液剪切速率较高,粘度较小。而在中心的流体剪切速率较小,轴线附近几乎为零,此时流体粘度很大表现为刚体的特性。对比图18这符合该阻尼器的流动工作模式[10],一定程度上说明使用的粘度模型和本次仿真的准确性。图14说明当0.17 s后坐停止时,激活区域非激活区流体粘度相差很大,体现了MRF的流变特性。激活区的磁流变液表现出刚体特性其流速几乎为零,起到“关门”作用。而在非激活区,流体由于惯性仍继续有较小的流动但受到“门”的阻碍,所以在碰撞后形成两股小绕流。 图18 流动模式示意图 4) 图17表明仿真误差在7%之内,在加速阶段效果较为理想,但在峰值和降速阶段有误差。误差之所以产生,可能是因为在模拟时,对结构简化造成。 模拟相同的冲击载荷,不同电流下工作腔与非工作腔的阻尼器工况,得出压力曲线。通过压强-力公式在Tecplot中得出阻尼力与时间曲线,如图19所示。 图19 阻尼力-时间曲线 从图19可以看出,阻尼力的峰值随着电流的增加而增加,而工作时间随着电流的增加而减小。这是因为随着电流的增大,粘度增大,流体对活塞的阻尼力增大。 1) 通过瞬态模拟对阻尼器内部流体的各项参数动态监测和控制,不仅可以节约实验成本,也有助于深入研究阻尼器的工作特性和磁流变液的粘度模型。 2) 文中提出的将UDF和基于区域整体相结合的模拟方法能够反映阻尼器内部实际流动特征和流动细节,对磁流变阻尼器的CFD瞬态模拟有参考意义。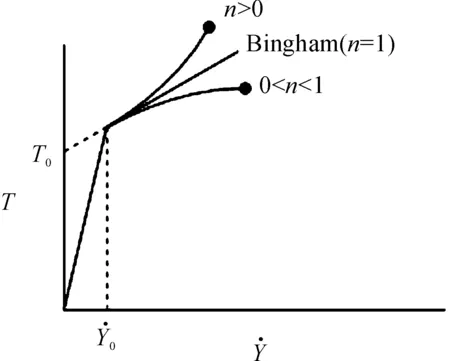
2 磁流变阻尼器的磁场模拟

3 磁流变阻尼器的流场模拟
3.1 计算模型的建立


3.2 计算方法

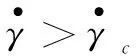
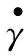
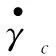
3.3 模拟结果



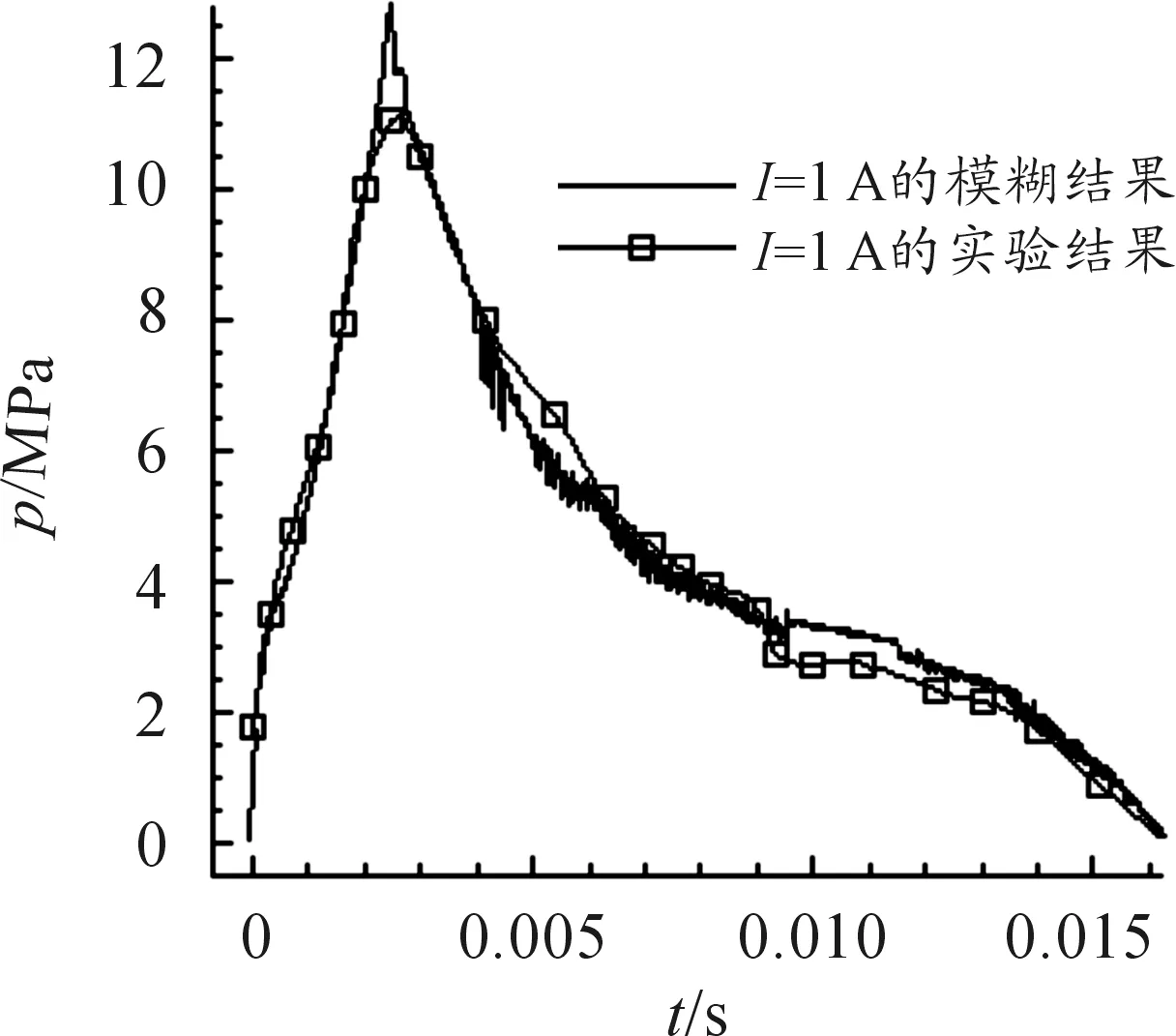
3.4 结果分析
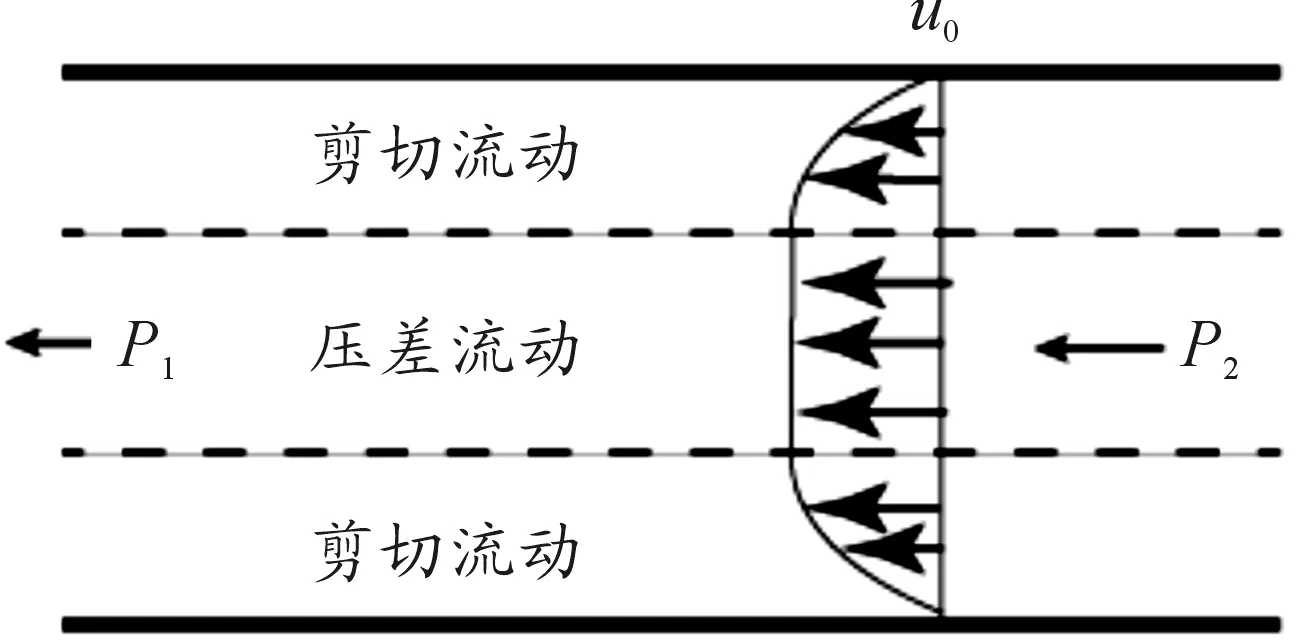
3.5 各电流下MRD阻尼力与时间关系
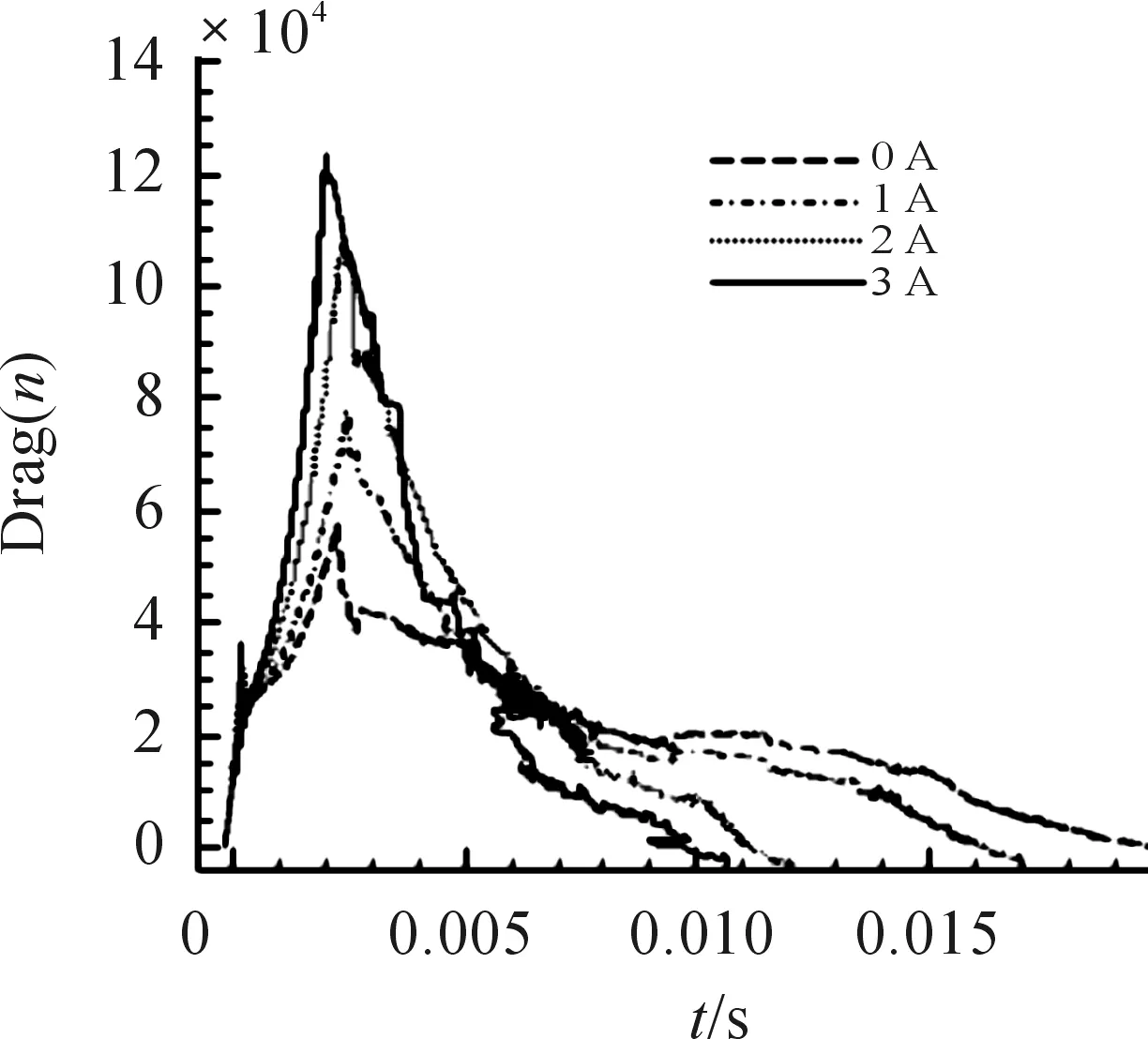
4 结论
