海洋目标单卫星探测系统分析

黄 璜，赵继广，魏 斌

(中国人民解放军战略支援部队航天工程大学， 北京 101400)

大海上目标包括商用用船、舰船、渔船等，海洋目标的监视大多使用光学、雷达和电子侦察卫星[1]。对于各种侦察手段来说，每种侦察系统都是不一样的。许多学者也是依据海洋目标的侦察系统开展了许多研究。吴炜琦、张育林等[2]建立了海洋目标探测卫星的通用性效能模型，该模型的依据是分析了影响目标探测概率的三类因素。徐一帆、谭跃进等[3]总结分析了天基海洋监视中的各种信息处理技术，并对于以后天基海洋监视的发展给了分析。万志、任建伟等[4]针对海洋目标，计算分析得出了侦察海洋目标最佳的宽波段为0.5～0.9 μm。

对于光学侦察卫星来说，它的一般分辨率都比较高，并且大多数海洋目标在光学图像上容易被区分。但图像的一般幅宽比较窄，气象条件对于光学成像的影响一般也比较大。所以对于一个单卫星侦察系统来说，衡量它的指标有很多，但要能准确反映出整个系统的特点则需要选取一些比较代表性的指标。

从前面分析也可以看出，对于海洋目标单卫星探测系统来说，首先就是要确定好侦察性能的指标，本文就是分析整个系统的信噪比和覆盖概率对整个海洋目标探测系统给出评价。

1 单卫星探测系统指标选取

对单卫星对地侦察进行能力分析，关键在于选取合理的评价指标。下面列举了以下几个关于探测能力的指标。

1) 调制传递函数

调制传递函数[5]用输出与输入图像间频谱之比来表示，它表示了天基光学探测系统再现空间目标的能力，包含确定图像质量的两个可测量数量，即图像的分辨率和对比度。光学探测系统以看作是一系列具有一定频率特性的子系统。总系统的传递函数等于各子系统传递函数之积。对于本文来说，其目的是对大海上目标卫星的探测能力分析。调制传递函数主要对系统的目标探测能力和识别能力进行分析。而本文着重分析相机系统的探测能力。因此本文不采用调制传递函数作为一个评价指标。

2) 探测距离

探测距离是指在一定探测条件下可以检测到目标的最大距离。在大多数光学探测系统性能分析中，探测距离被用作衡量设备的目标探测能力的重要指标[6]。探测距离与目标状况、外界环境、光学系统和探测器的性能参数等有关。系统所获取的信号强度与探测距离成反比，即距离越远，获得信号越弱，对目标的探测越困难。对于本文来说，以探测距离作为指标因覆盖面不全而使评价效果降低。

3) 虚警概率和探测率

虚警通常发生在系统对空间目标进行探测时，错误的将非目标认定为目标，或在没有目标的情况下误报发现目标[7]。虚警概率表示为误报的非目标数与实际存在的非目标数的比值。

探测率是光学探测系统探测能力的最终结果体现，探测率的大小能够最直观地描述系统的探测能力。探测率的大小与虚警概率有很大的关系，在探测结果分析中可表示为认定目标数与实际存在的目标数的比值[7]。

探测率与虚警概率在系统工作时能够衡量系统最终的探测能力，但是它们无法很好地与对地观测目标光学探测系统的焦距、视场等性能参数建立联系，并且本文只是对单卫星对海洋目标进行侦察，所以不满足本文对探测能力分析的要求。

4) 信噪比

系统对目标进行探测时，目标到达系统的信号与整体噪声的比值称为探测信噪比。光学探测系统执行目标探测任务时，是否能够探测到目标是系统探测能力高低的直接体现。在一定空间环境及探测条件下，要使目标能被探测到，首先应使其在接收面上的光能量(或照度)能被系统的接收器感受到，此外，像面上目标和背景的对比度要达到一定的比值要求，此即信噪比(SNR)最关心的问题。

而光学遥感图像信噪比是光学遥感器获取数据质量的重要评估标准，是对光学遥感器信噪比的实际评估。它主要取决于仪器的性能，还与环境条件、大气条件等其他因素有关。图像数据的信噪比可以在在很大程度上反映遥感器的信噪比性能。

5) 分辨力和灵敏度

有4中不同的分辨力：一是时间分辨力，表示按发生时间区分事件的能力；二是灰度级分辨力；三是谱分辨力；四是空间分辨力。其中对于卫星探测能力来说，时间分辨力是指卫星系统对多个目标重复侦察的时间间隔，探测目标时间分辨能力是时间分辨力的倒数。

灵敏度是有关可以测量的最弱信号。取在系统输出端产生的信噪比为1的信号为其值。灵敏度取决于光学系统收集光线的特性、探测器的响应以及系统的噪声，与分辨力无关。而系统整体的响应取决于分辨力和灵敏度。

6) 地面覆盖率

对于单卫星侦察海洋目标来说，地面覆盖率表示在任务时间内对任务区域覆盖到的面积和任务区域之比。这对于单卫星侦察来说，也是目标是否能被侦察到的第一步。这也是单卫星侦察海洋目标的基础。

综上所述，本文着重分析单卫星系统的信噪比以及单卫星的在一定时间内的覆盖率。

2 单卫星探测系统信噪比模型建立

对于对地侦察来说是一个复杂的光电转换过程。具体过程如图1所示。

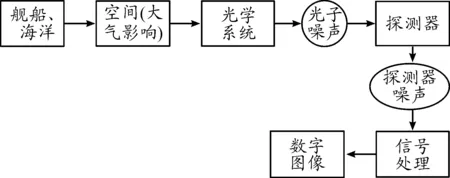
图1 光电转换图

因此，如果要建立海洋目标的信号探测模型，就要对光电转换的各个环节进行分析。而对于整个探测系统来说，就是要建立从太阳辐射、目标散射、大气衰减、相机入瞳以及相机镜头衰减、到达探测器最后信号处理形成图像整个过程的物理模型。

对海洋目标光学探测系统的探测信噪比不仅与系统自身性能密切相关，同时还受到外界观测条件、环境等因素的影响。图2给出了对地目标光学探测系统信噪比与系统影响因素之间的关系。

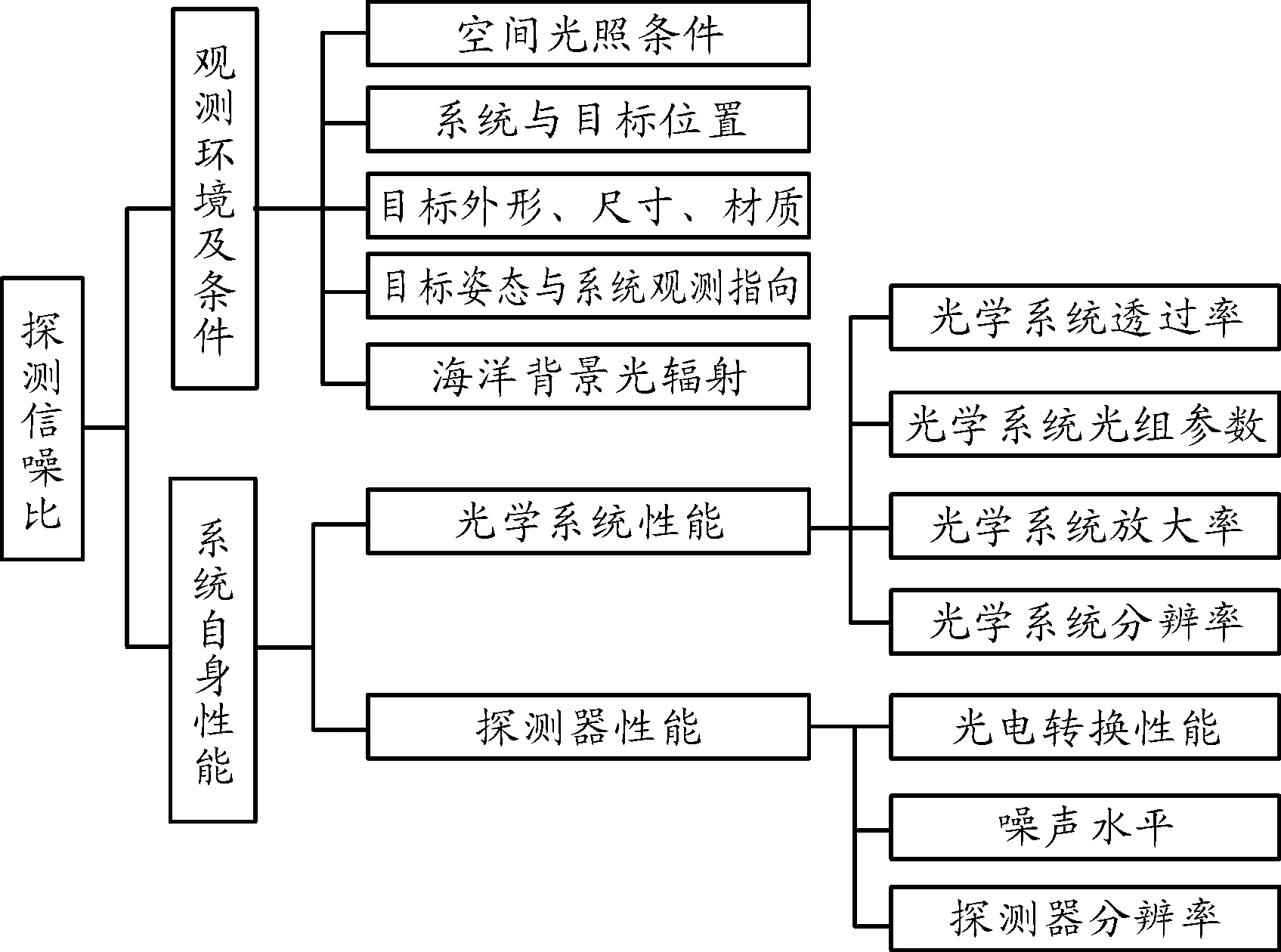
图2 探测信噪比影响因素图

2.1 空间光照条件

在计算太阳的辐射出射度时，通常认为太阳是一个绝对温度为 5 900 K的黑体。根据普朗克黑体辐射公式，太阳在一定光谱范围内的辐出度为[8]：

(1)

式(1)中，λ1、λ2为光谱范围；T=5 900 K为太阳的黑体温度。通过引入第一辐射常数C1=2πhc2=3.742×10-16W·m2，和第二辐射常数C2=hc/k=1.434 88×10-2m·k，上式可以化简为：

(2)

假设太阳的辐射出射度在空间各个方向上是均匀分布的，则太阳在λ1～λ2光谱范围内的辐射强度为[9]：

(3)

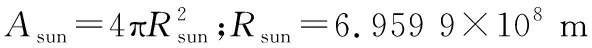
根据距离平方反比法则，太阳对海洋目标的辐照度为：

(4)

式(4)中，Dreal为卫星到海洋目标的距离。

2.2 信号探测模型

设目标卫星-探测系统连线与系统光轴方向的夹角为θ，Et为海洋目标在单卫星探测系统入瞳处产生的辐照度，则光学系统的物面照度为：

Eobj=Et·cosθ

(5)

夹角θ大小与系统的视场角有关，当视场角较小时，夹角θ可以忽略不计。

设光学系统镜头口径为D，透过率为τo，焦距为f′，则光学系统的像面照度为[10]：

(6)

设探测器接收到的辐射均匀地分布在M个像元上,Mte为探测器像元总个数，Ate为探测器像元阵列总面积，则目标在探测器上单色光谱的辐射功率为：

(7)

则此时单色光谱反射造成的传感器输出信号的光电子数为：

(8)

因此，目标可见光反射辐射造成传感器输出信号的光电子数为：

(9)

式(9)中，QE(λ)为探测器的量子效率；FF为探测器的填充因子；τint为积分时间；v为光电子离开探测器表面时的速度，近似等于光速c；λ为光谱波长。

2.3 系统噪声模型

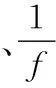
1) 光子噪声

光子噪声[11](Shot Noise)又称散粒噪声，源于光子流的随机性质。光子噪声与频率无关，因而不会限制器件的动态范围，但是它决定了光学检测系统的噪声极限值，特别是当光学探测系统工作在低照度、低反差的条件下，由于采取一切可能措施降低各种噪声，光子噪声成为主要的噪声源。光子噪声的主要来源为目标反射信号和暗电流信号。设ND为暗电流产生的光电子数，Nobj为目标反射产生的光电子数。则光子噪声为：

(10)

2) 热噪声

热噪声(Thermal Noise)是电子的随机运动引起的，所有温度的半导体，无论是否有外加电流通过，都有热噪声，所以几乎所有电路中都存在热噪声，影响信号的传输。热噪声是覆盖整个频率范围的白噪声。热噪声产生的光电子数目表示为[12]：

(11)

式(11)中，B为热噪声等效带宽，由于热噪声覆盖整个频率范围，所以B是由电路工作带宽所决定的；R是电阻值；k是波尔兹曼常数；T是电阻的绝对温度；τint为积分时间；q为单位电荷电量；Ntn为观测时段内热噪声累计产生的电子数目。

3) 复位噪声

图像传感器在工作时，每帧数据读取完毕，进行下次光信号采集之前都先要对光敏元件进行复位。在复位开关与低电阻电源断开时，部分电荷会残留于电路电容上。下一次开关打开时，噪声将在电阻的输入端引入，这就是复位噪声[13]。复位噪声可以用电子数目的方式近似表示为：

(12)

式(12)中，k为波尔兹曼常数；T为电容绝对温度；C为电路电容大小。因此复位噪声也被称为KTC噪声。

4) 1/f噪声

1/发f噪声，又称闪烁噪声、低频噪声。对于MOS晶体管，栅氧化层和硅衬底的界面处的电子会被界面处的能态随机地俘获，随后又被这些能态释放。结果在漏电流中产生了“闪烁”噪声。闪烁噪声的平均功率不容易预测。1/f噪声也可用光电子数目表示为[13]：

(13)

式(13)中，Ks是一个与工艺有关的常量；W×L为器件面积；Cox是单位面积的电容；R2与频率f成反比，所以该噪声称为1/f噪声。

5) 固定模式噪声

固定模式噪声(FPN)是由于器件的失配，即空间非一致性造成的，它不随图像帧变化而变化，对所有图像帧的影响都一样[14]，故称其为固定模式噪声。

光照条件下固定模式噪声FPN包括偏移和增益两部分。其中偏移部分就是暗信号非一致性，为常数；增益部分是光响应非一致性，它的幅度随着光强而变化。它们之间有如下关系[13]：

NFPN=NDSNU+NPRNU

(14)

综上可知，可知整个探测系统的噪声为：

(15)

最后可知单卫星探测器的信噪比模型为：

(16)

3 单卫星覆盖模型

卫星的覆盖模型如图3所示。

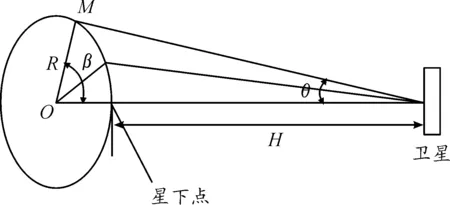
图3 覆盖模型图

图3中，θ为卫星的视场半角，β为卫星的对地面的覆盖角。在不考虑卫星侧视情况下，则探测器在地球表面所探测的区域如图3区域。

(17)

对于相机侧摆成像仪、扫描式成像仪、推扫式成像仪的成像模式都为球面四边形覆盖模式。如图4所示。

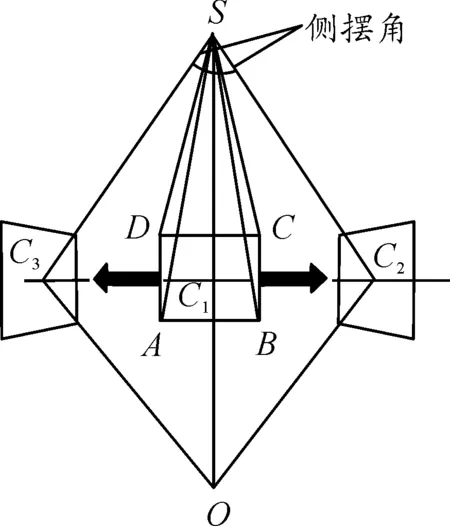
图4 卫星扫描图

由图4可知，ABCD为卫星扫描区域，O1为星下点，O为地心，扫描区域在侧摆角的作用下发生了改变。所以只要计算ABCD成像点经纬度即可。见图5。

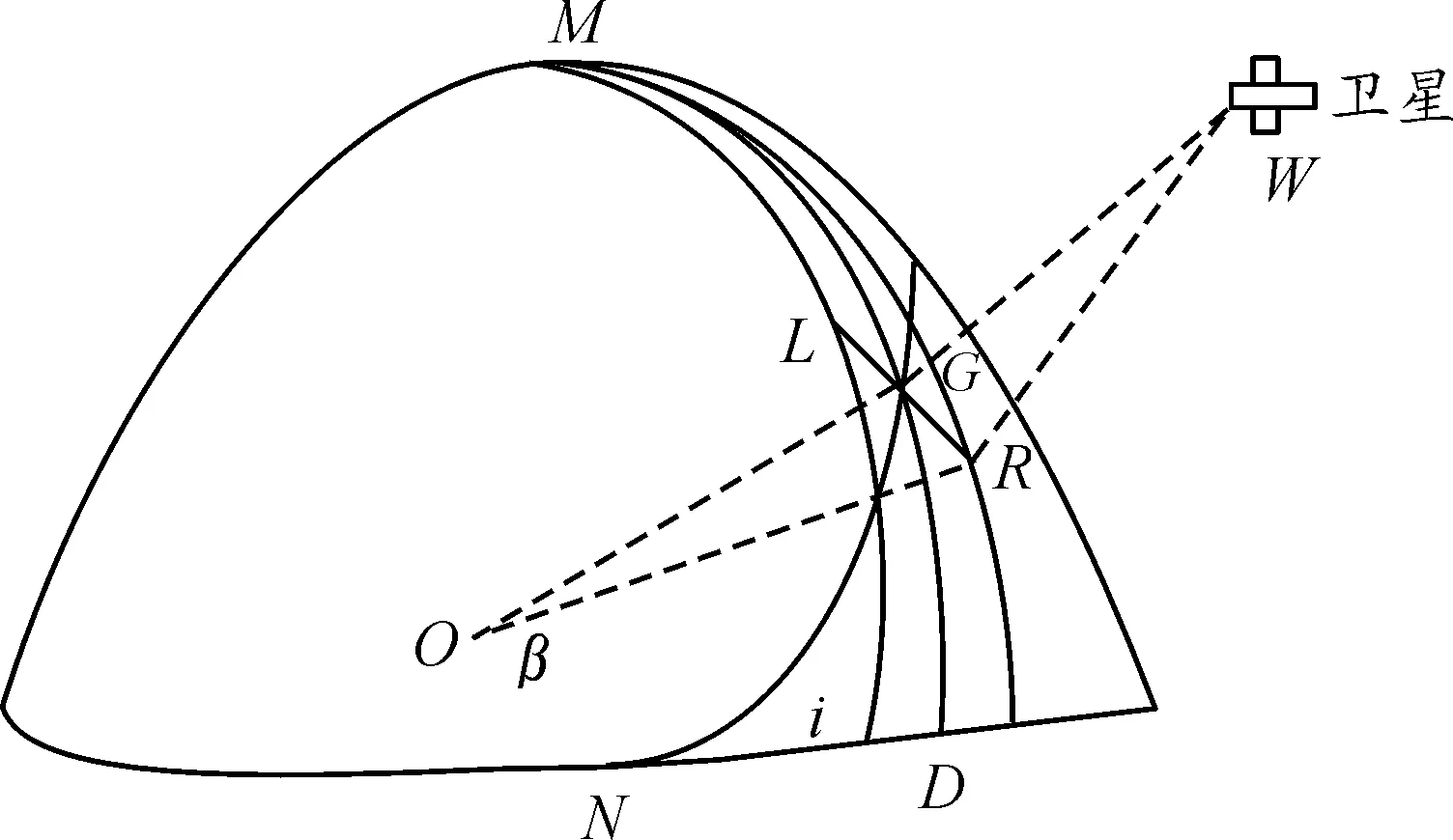
图5 成像经纬度示意图

图5中，M为北极点，N为轨道生交点，某时刻卫星的星下点的赤经和赤纬分别为α和δ，方位角为A，赤经圈与赤道的交点为D。过G作垂直于星下点的大圆弧，在大圆弧上与G的角距为β的点分别为L(αL,δL)，R(αR,δR)。随着卫星的运动，则L、R形成的轨迹即为覆盖带的外沿轨迹。根据球面三角形余弦公式的得：

cosMR=cosMGcosGR+

(18)

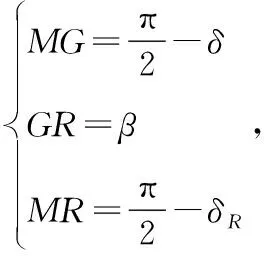
sinδR=sinδcosβ-cosδsinβsinA

(19)

已知卫星在该时刻的轨道根数，在直面球面三角形NGD中，有

(20)

代入式(19)消去A可得R点的赤纬为：

sinδR=sinisinμcosβ-cosisinβ

(21)

同样可得L点的赤纬为：

sinδL=sinisinμcosβ+cosisinβ

(22)

则在L和R点纬度情况下以及星下点G的经纬度情况下，确定L和R的经度。

cosGR=cosMGcosMR+sinMRsinMGcos(λR-λG)

(23)

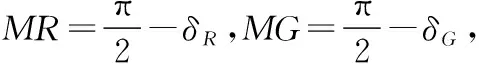
cosβ=sinδRsinδG+cosδRcos(λR-λG)

(24)

(25)

同样可得到L点的经度为

(26)

因此当知道星下点的经纬度和覆盖地心角，有上面推导可知，先计算出L、R的纬度δL、δR，再计算出经度λL、λR。关于(25)、(26)正负号的规定，当轨道倾角i>90°，(1)式取“+”，(2)式取“-”；当轨道倾角i<90°，(1)式取“-”，(2)式取“+”。

对地覆盖率的计算，大多都是采用网格点分析法，结合前面分析的依据卫星星下点经纬度计算对地覆盖的边界点。

网格点分析法。就是将所要探测的区域按一定比例分为许多个点，每个点的经纬度(λi,φi)，卫星覆盖的区域为M，如果(λi,φi)在M确定的区域内，则该网格点被覆盖，否则没被覆盖。其中采用面积覆盖率来表示单卫星对地覆盖情况。

面积覆盖率指在网格点的覆盖区域内，每个点代表的面积几乎相等。所以在仿真的过程中将探测到网格点Ncover,区域内的总网格点数为Ntotal，则在仿真时间内对该区域内的覆盖比为Pfu为：

(27)

4 仿真分析

为了对单卫星的信噪比做一个静态下的计算，参照STAR1000传感器，设定计算参数如表1所示。系统SNR静态计算结果如表2所示。

假设系统采取了抑制外部噪声的措施，外部噪声已经很小，因此，模型中暂不考虑外部噪声的影响，光子噪声中只包含目标反射产生的光电子数和暗电流产生的光电子数，如表2所示。

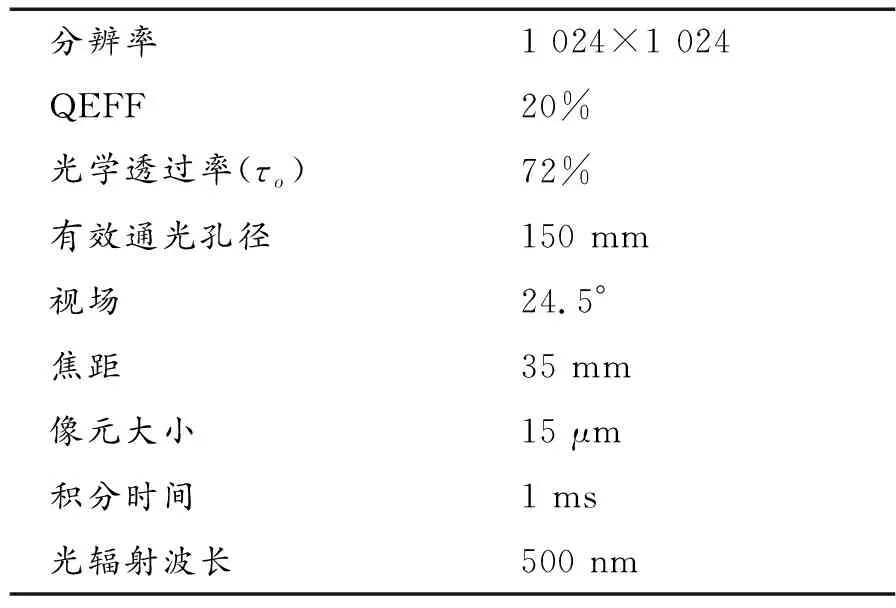
表1 卫星传感器参数

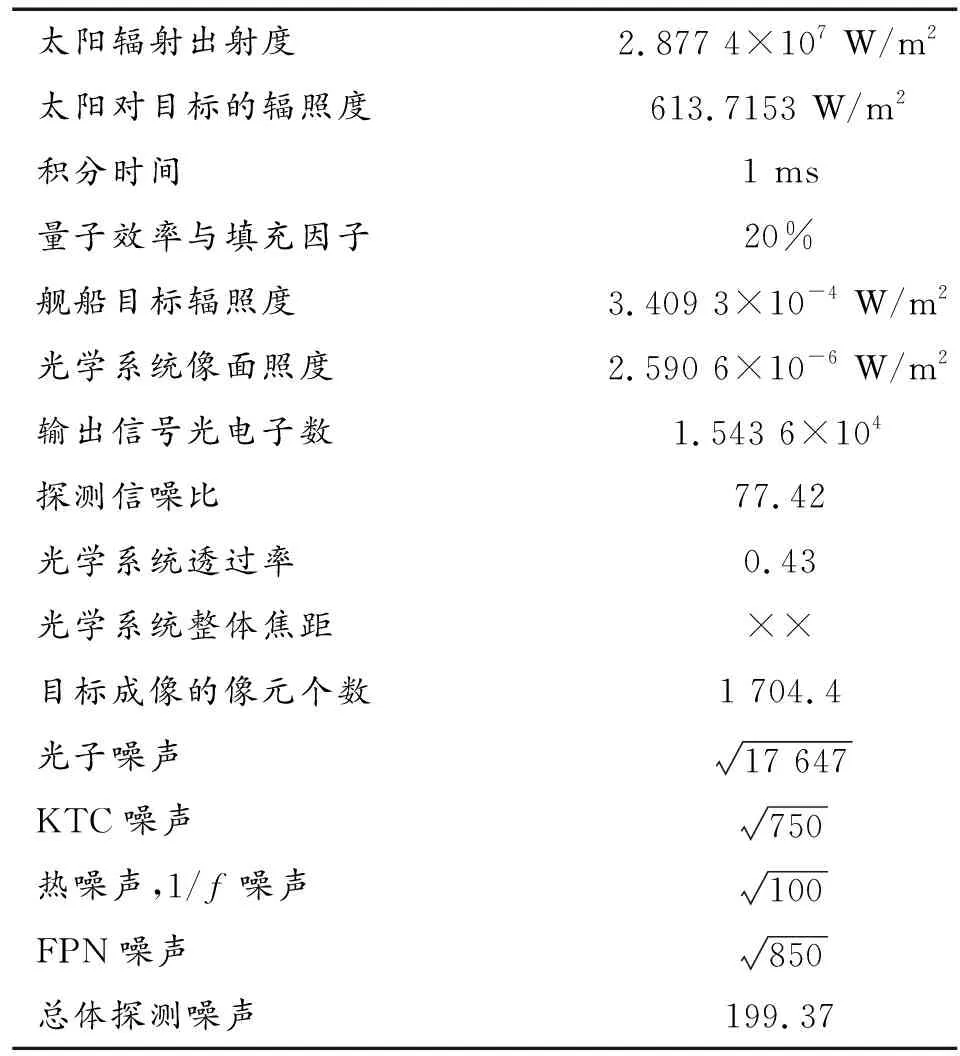
表2 系统SNR静态计算结果

对于单卫星的覆盖情况，采用STK软件对一特定区域进行了仿真，并且计算了初始时刻卫星覆盖边界点的经纬度与覆盖模型计算得到的边界点的经纬度做了一个比较。具体参数如表3所示。

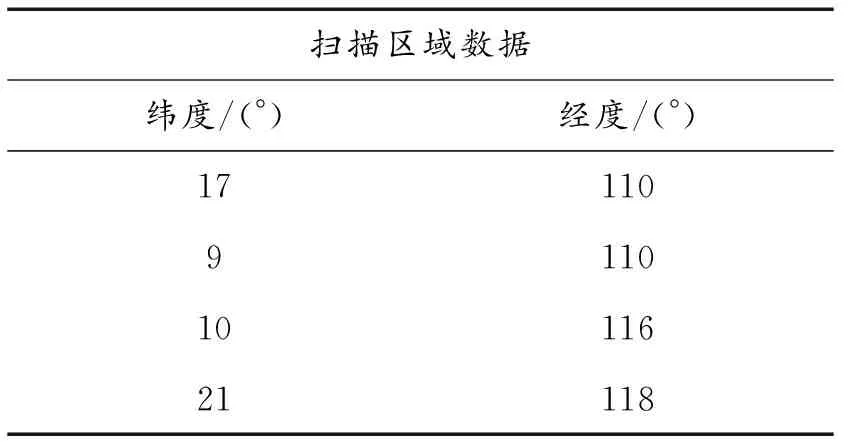
表3 扫描区域设置参数

在初始时刻，卫星扫描区域边界点的经纬度比较如表4所示。

表4 仿真结果对比

从上面表格可以看出，所建立的地面覆盖模型的计算结果与STK仿真结果相差很小，这也从一方面验证了所见对地覆盖模型的适用性。

设置卫星扫描时间为一天，探测器的为矩形扫描，视场角为5°。通过一天的扫描得到了最后总的覆盖率达到了84.59%。具体情况如图6所示。

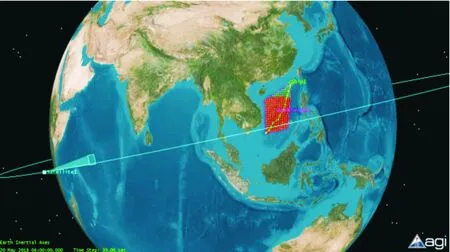
图6 STK仿真示意图

5 结论

1) 本文选取了信噪比和对地覆盖率两个指标。一方面建立了单卫星探测器的信噪比模型，并计算了静态情况下的SNR值。另一方面依据STK软件，验证了所建对地覆盖模型的适用性。为分析和研究天基对海洋目标侦察提供了理论依据。

2) 本文没有仿真出动态情况下的SNR值的变化，在计算对地覆盖模型时，没有考虑探测器背景以及目标背景对信噪比模型的影响。所以以后在分析天基系统时应该将背景考虑进去，并要着重考虑探测器本身对探测系统带来的影响。