非线性偏微分方程的精确行波解
2019-02-25王书敏薛瑞梅姚若侠
王书敏,薛瑞梅,姚若侠
(陕西师范大学 计算机科学学院,陕西 西安 710119)
0 引 言
20世纪60、70年代,人们对非线性问题共性的研究形成了一个交叉学科—非线性科学[1]。利用计算机符号计算[2]和自动推理技术,非线性科学研究取得了巨大的进步。目前,国际上比较有代表性的符号计算软件有:MACSYMA,REDUCE,mu-MATH,Maple,Mathematica,Matlab,Python等。Maple是由加拿大滑铁卢大学和Maplesoft公司共同研发的科学计算软件,内置高端技术解决建模和仿真中的数学问题,具有强大的符号计算和数值演算功能,以及交互式编辑环境。
对非线性偏微分方程的研究是非线性科学研究的重要分支,涉及生物学[3]、物理学[4]、力学[5]以及计算机科学[6]等领域。求解非线性偏微分方程的精确行波解是其中的一部分,现有的求解方法有:齐次平衡法[7-8]、指数函数法[9-11]、反散射变换法[12]、Darboux变换法[13]、辅助函数法[14]等。
文中应用Maple软件的PDEtools工具包进行辅助函数算法的应用,plots工具包模拟方程解的三维图形。通过修正算法中参数m的取值范围,研究Benjamin-Bona-Mahony方程(BBM方程)[15]行波解的变化。BBM方程是由Benjamin、Bona和Mahony于1972年研究提出的一个正则化的非线性长波方程,作为改进的KdV方程,主要用于对1+1维上单向传播的小振幅重力波进行建模。
1 修正的辅助函数算法分析
采用辅助函数算法求解如下形式的非线性偏微分方程:
P(u,ut,ux,uxt,uxx,utt,…)=0
(1)
其中,u=u(x,t)是势函数;P是关于u(x,t)及其各阶偏导数的多项式,具体步骤如下:
步骤1:利用行波变换u(x,t)=u(ξ),ξ=kx+ct,其中ξ为行波变量,c为波速,将方程1转换为如下常微分方程:
P(u,u',u'',…,u(n))=0
(2)
步骤2:通常,假设式2有如下形式的解:
(3)
文中修正m的取值范围,即假定式2有如下形式的解:
(4)
其中,ai是待定常数;m可以通过齐次平衡法求得。
假设f(ξ)满足辅助常微分方程:
f(ξ)'=f(ξ)2+λf(ξ)+μ
(5)
方程5具有如下不同形式的解,其中C0是积分常数。
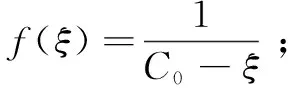
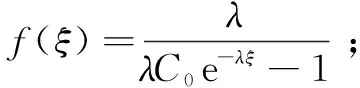




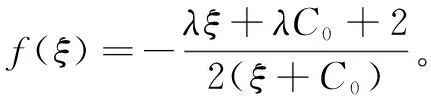
步骤3:两种情形下,分别将式3和式5、式4和式5代入式2,合并方程左端关于f(ξ)的多项式,并令各幂次项系数等于零,得到关于k,c,ai的代数方程组。
步骤4:借助Maple求解步骤3中的代数方程组,将求得的参数k,c,ai和式5的解代入式3和式4,即可得到非线性偏微分方程(式1)的行波解。
2 算法应用与实现
调用Maple软件的PDEtools工具包,根据第1节中的算法步骤,考虑如下形式的BBM方程[15]。
ut+αux+βuux-γuxxt=0
(6)
其中,α,β和γ是非零任意常数,将行波变换u(x,t)=u(ξ),ξ=kx+ct代入式6可得到如下常微分方程:
cu'+αku'+βkuu'-γck2u'''=0
(7)
利用齐次平衡法确定m=2。
情形1:将m=2代入式3,式7有如下形式的解:
u(ξ)=a0+a1f(ξ)+a2f(ξ)2
(8)
将式8和式5代入式7中,按照前述方法,Maple符号计算代码如图1所示:

图1 Maple符号计算代码
得到一个代数方程组并求解,得到参数k,c,ai(i=0,1,2)的解如下:

a1=a2λ,a2=a2
将参数解和辅助方程(式5)的解代入式8,即可获得BBM方程的精确行波解,其中ξ=kx+ct。调用Maple软件的plots工具包,设置参数值,即可得到解的三维图。
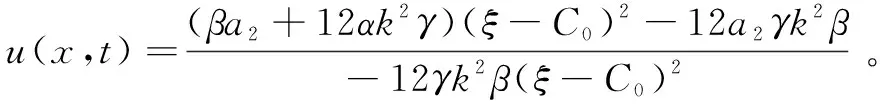

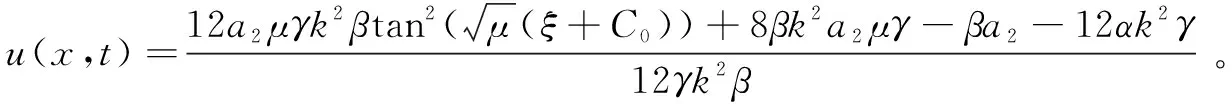
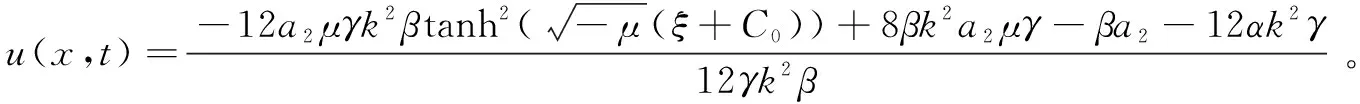
取k=1,a2=1,μ=-12,α=1,γ=1,β=1,C0=0,对应的三维图如图2所示。

图2 三维图(1)
解5:当λμ≠0,λ2>4μ时
取k=1,a2=1,λ=4,μ=3,α=1,γ=3,β=1,C0=1,对应的三维图如图3所示。
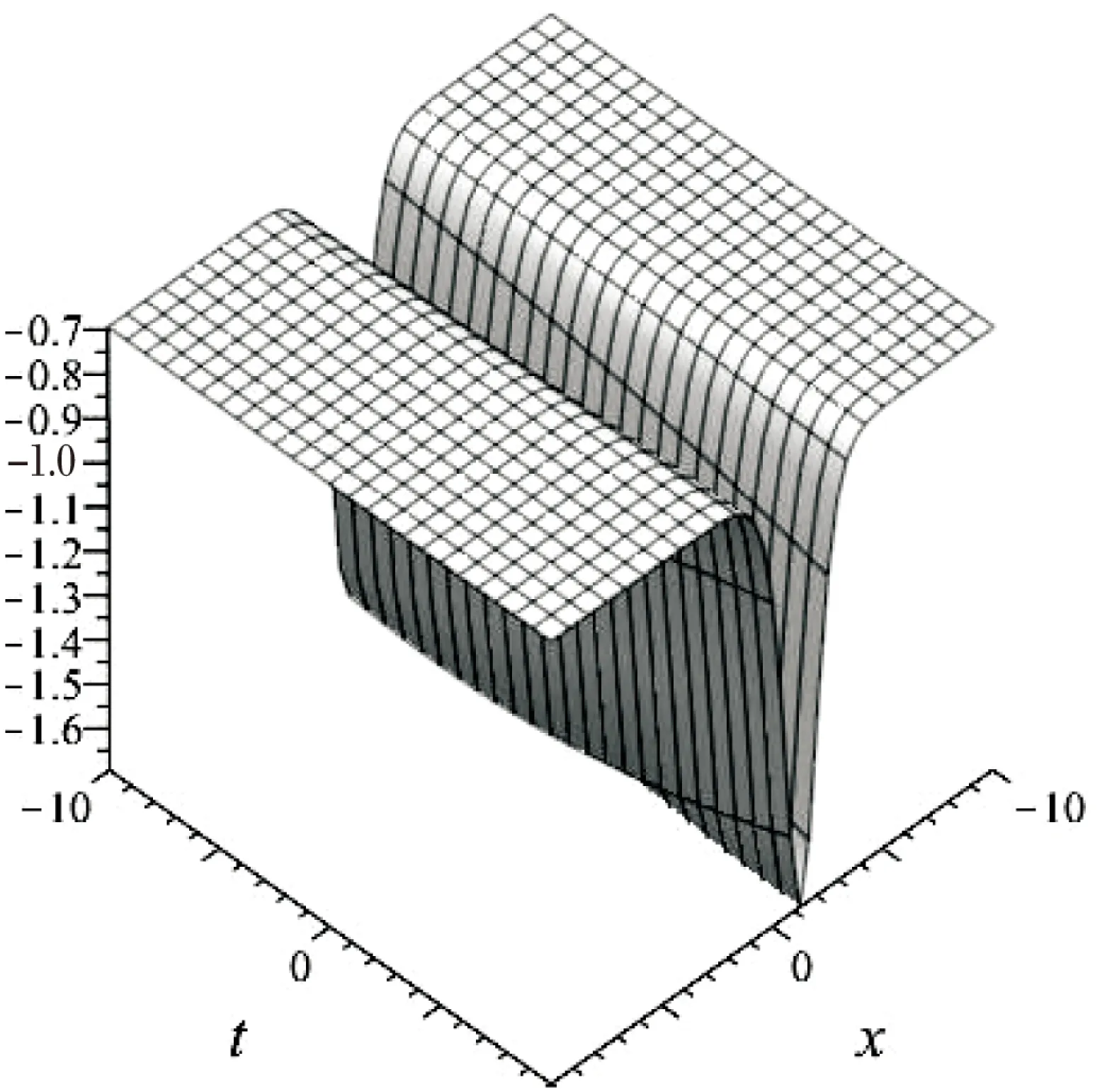
图3 三维图(2)
解6:当λμ≠0,λ2<4μ时,

情形2:把m=2代入修正m取值范围的式4,则式7解的形式如下:
u(ξ)=a-2f(ξ)-2+a-1f(ξ)-1+a0+
a1f(ξ)+a2f(ξ)2
(9)
将式9和式5代入式7,具体求解过程及大致Maple代码如上所述,求得参数k,c,ai(i=-2, -1,…,2)的四组解:
第一组解:
第二组解:
第三组解:
第四组解:
对比以上四组参数解,第一组和第三组中a-2和a-1取值为零。研究表明,第一组和第三组参数解求得的BBM方程行波解与情形1获得的方程行波解在形式上相似。故以第二组解为例,求解并获得BBM方程的精确行波解如下,其中ξ=kx+ct。
解1和解2两种情况求得的解分别为零和常数,以下不做列举。


解5:当λμ≠0,λ2>4μ时,
u(x,t)=
解6:当λμ≠0,λ2<4μ时,
u(x,t)=
取k=1,λ=4,μ=5,α=2,β=1,γ=1,C0=1,对应的三维图如图4所示。
解7:当λμ≠0,λ2=4μ时,
取k=1,λ=4,μ=4,α=2,β=1,γ=1,C0=1,对应的三维图如图5所示。
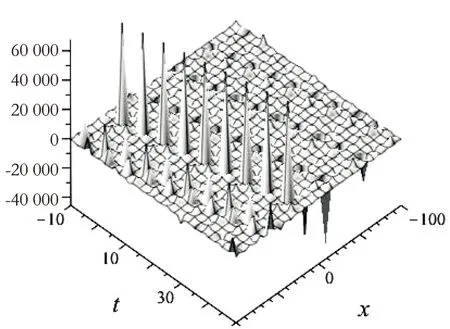
图4 三维图(3)
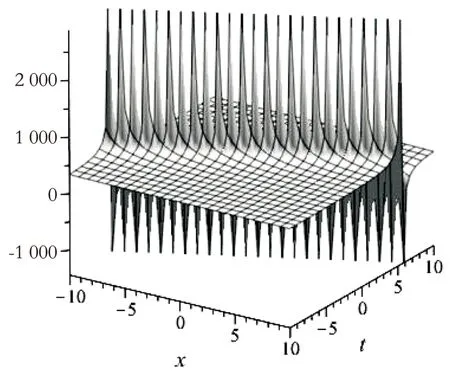
图5 三维图(4)
3 结束语
借助符号计算系统Maple的PDEtools工具包计算BBM方程精确行波解,通过修正辅助函数算法,研究方程解的变化。对比修正参数m取值范围前后,情形1获得一组参数解,情形2获得四组参数解,进而情形2求得了更为丰富的方程行波解。通过plots工具包,情形2求得的方程解的三维模型图更加有利于人们对非线性现象的探究。
