An Entity-Association-Based Matrix Factorization Recommendation Algorithm

Gongshen Liu, Kui Meng, , Jiachen Ding, Jan P. Nees, Hongyi Guo and Xuewen Zhang

Abstract: Collaborative filtering is the most popular approach when building recommender systems, but the large scale and sparse data of the user-item matrix seriously affect the recommendation results. Recent research shows the user’s social relations information can improve the quality of recommendation. However, most of the current social recommendation algorithms only consider the user's direct social relations,while ignoring potential users’ interest preference and group clustering information.Moreover, project attribute is also important in item rating. We propose a recommendation algorithm which using matrix factorization technology to fuse user information and project information together. We first detect the community structure using overlapping community discovery algorithm, and mine the clustering information of user interest preference by a fuzzy clustering algorithm based on the project category information. On the other hand, we use project-category attribution matrix and user-project score matrix to get project comprehensive similarity and compute project feature matrix based on Entity Relation Decomposition. Fusing the user clustering information and project information together, we get Entity-Association-based Matrix Factorization (EAMF) model which can be used to predict user ratings. The proposed algorithm is compared with other algorithms on the Yelp dataset. Experimental studies show that the proposed algorithm leads to a substantial increase in recommendation accuracy on Yelp data set.

Keywords: Collaborative filtering, matrix factorization, recommender system.

1 Introduction

With the rapid development of information technology and Internet, we gradually move into the era of big data. To extract valuable information from massive amount of data is a big challenge for both information consumer and information provider. The recommender system is developed to help users find their interested information, and let information provider target their customers more efficiently, which is a win-win solution. At present,the recommender system has been widely adopted to several Internet fields [Ricci, Rokach,Shapira et al. (2011)].

The recommendation algorithm is the core of a recommender system. The collaborative filtering (CF) recommendation algorithm is one of the most successful recommendation technologies [Su and Khoshgoftaar (2009)]. The fundamental assumption of CF is that if user X and Y give similar rates tonitems, or have similar behaviors (e.g. buying, watching,and listening), they will give similar rate on other items. CF recommendation algorithm divides users with similar behavior, and recommends items to them. Versus the contentbased recommendation algorithm, CF recommendation algorithm is not limited by the content analysis technology. However, CF recommendation algorithm faces the challenges such as data sparsity, scalability, synonymy, and gray sheep [Su and Khoshgoftaar (2009)].The rapid expansion of Internet and its users even make these worse.

Social network analysis shows that users of the same community often show a similar interest and behavior characteristics because of social factors [Krebs (2017)]. Therefore,in recent years the socialization recommender system with user’s social attributes has become the research hotspot in recommender system. Usually traditional trust-based socialization recommendation algorithm only utilizes direct trust relationship among the users. With Internet scale increasing, the direct trust relationship between users becomes sparse inevitably. Moreover, the basic assumption of a trust-based socialized recommendation algorithm is that the user’s interest preferences are similar to or are affected by their trusted users [Yang, Guo, Liu et al. (2014)]. In fact, the user's interest preferences are multifaceted, and usually are different from each other. A single direct social relationship could not characterize the difference exactly.

In this paper, we propose a recommendation algorithm named Entity-Association-based Matrix Factorization (EAMF) that integrates user information and project information together. We use overlapping community discovery algorithm to find user's community information, which avoids the sparseness of data caused by the use of direct social relations, and cluster user interest preference based on the project category information considering the user preference differences of the same community. These two kinds of information are merged together to cluster user character. On the other hand, we use project-category attribution matrix and user-project score matrix to get project comprehensive similarity and compute project feature matrix. Fusing the user clustered character and project feature matrix together, we get Entity-Association-based Matrix Factorization (EAMF) model which can be used to predict user ratings.

2 Related works

The traditional collaborative filtering recommendation algorithm is divided into memorybased method and model-based method [Bobadilla, Ortega, Hernando et al. (2013)]. In recent years the collaborative filtering recommendation algorithm based on the matrix decomposition model has been widely used as a branch of the model-based method. It can transform high-dimensional user-project scoring matrix into low-dimensional matrix product which represents the implicit eigenvector of user and project, and relieves accuracy decreasing caused by sparse data. The application of matrix decomposition technique in recommender system is first proposed in Koren et al. [Koren, Bell and Volinsky (2009)]. The probability matrix decomposition model is proposed in Salakhutdinov et al. [Salakhutdinov and Mnih (2007)].

In socialization recommendation algorithm, the matrix decomposition technique is combined with various social attribute of users. It gets better user implicit eigenvectors by adding the correlation constraints in the process of matrix optimization decomposition,which assumes that user and their trusted users have similar interest preference or are affected by each other. SoRec model is proposed in Ma et al. [Ma, Yang, Lyu et al.(2008)]. It is a type of social spectrum regularization deformation method, which applies matrix decomposition technique to trust matrix. The user implicit eigenvector is generated during the decomposition optimization of user-project scoring matrix and trust matrix. STE model is proposed in Ma et al. [Ma, King and Lyu (2009)]. In STE, the items in the user-project scoring matrix are the combination of user’s personal preference and their trusted friend’s preferences. In the decomposition optimization, it get a weighted average of the users’ score and his friends’ score to the same item, which makes the recommendation results interpretable. SocialMF model is proposed in Jamali et al.[Jamali and Ester (2010)]. It assumes that the implicit eigenvector of the user is determined by the implicit eigenvector of his friend, and defines the concept of trust propagation during the decomposition optimization. However, these socialized recommendation algorithms use only the user’s direct social relationship. When direct social relationship is sparse, the recommendation results will be unacceptable. Yang et al.improve SocialMF model [Yang, Steck and Liu (2012)]. They distinguish user categoryspecific social trust to different items and different friends, and divide friend circle according to the items they rated, which further intensify the problem of data sparsity.Guo et al. take the characteristics of trust diversity into consideration [Guo, Ma and Chen(2013)], and propose a trust strength aware social recommendation method, StrengthMF,assuming that a trust relation does not necessarily guarantee the similarity in preferences between two users. StrengthMF can acquire a better understanding of the relationship between trust relation and rating similarity, but the algorithm is still limited by the problem of direct social relations sparsity. Li et al. [Li, Wu, Tang et al. (2015)] introduce overlapping community discovery algorithm into the socialization recommendation algorithm. They focus on the constraint of regular term in objective function, and propose two models to reduce the impact of preference difference among users in the same community. Huang et al. propose an overlapping community detection algorithm named LEPSO [Huang, Li, Zhang et al. (2017)], which is a meta-heuristic approach, combining line graph theory, ensemble learning, and particle swarm optimization (PSO) together.They transform the overlapping community detection problem into a disjoint community detection problem on line graph, and use ensemble clustering techniques to optimize modularity of the line graph. Li et al. [Li, Zhang and Li (2017)] use both user generated contents and relationships between users to build a probabilistic user interests model,design a user interest propagation algorithm (UIP), and combine the UIP algorithm with classical matrix factorization to form a new rating prediction method, namely MF-UIP.Experimental studies show that MF-UIP outperforms existing algorithms.

3 Matrix factorization recommendation algorithm based on internal entity relationship

The flow of our Entity-Association-based Matrix Factorization (EAMF) recommendation algorithm is shown in Fig. 1.

Firstly, the overlapping community discovery algorithm is used to obtain the community structure of the social network, and so we get the user cluster based on community structure. According to project category information and user behavior record, the user preference vector is synthesized with the category distribution vector and the category professional vector. Using the fuzzy C-mean clustering algorithm, we get the user cluster based on interest preferences. Then, we can quantify target user’s preferences to above user clusters it belongs to, here is community structure based user cluster and interest preference based user cluster, and regularize these two user clusters respectively.

Figure 1: The flow chart of matrix factorization recommendation algorithm

On the other side, we calculate Scoring-based project similarity with users’ historical rating information, and Category-based project similarity with project category information respectively. It is easy to obtain project relevance based on comprehensive similarity (project similarity clustering) and project feature matrix.

With these two kinds of information, user-based and project-based, we can use matrix decomposition model of fusion entity-related information to forecast the user’s interest to the project.

3.1 Problem definition

We represent, U={u1, u2,…,um} as the set of all users in the recommender system;

V={v1,v2,… ,vn} represent the set of all projects; C={c1, c2,… ,cq} represent the set of all project categories; andm, n, qrepresents the number of users, projects and categories respectively. R=(Rij)m×n,Rij∈ {1,2,3,4,5}, represent user-project score matrix, and

Rijrepresents user ui’s score to the project vj. T=(Tij)m×m,Tij∈ {0,1} represent the user’s social relation matrix, and Tij=1 represents user uiand user ujare friends. We require a bidirectional confirmation of the user's social relations, so the matrixTis a symmetric matrix.

3.2 Clustering based on community structure

In recommender system, user clusters and the social links between users constitute a large social network. Usually, it is assumed that the user and its direct friends often have similar interests, or may influence each other. Base on such assumption, some researches[Ma, Yang, Lyu et al. (2008); Ma, King and Lyu (2009); Massa and Avesani (2004)] add user’s social relations information to optimize traditional collaborative recommendation algorithms. However, in large-scale social network, there exists a long tail effect[Fortunato (2010)], that is, only a few social users have many social relations, and the vast majority of users only have a small number of social relations. Therefore, it is necessary to dig out other valuable information from the social network, where there is community structure in social network. Users in the same community share the same characteristics, such as similar geographical location, same industry sector, or common interest topics, and have more or less impact on each other. Moreover, users inevitably belong to multiple communities. Such overlapping communal information reflects different characteristics of a user.

Research on overlapping communities in social network is a hotspot in the field of community discovery in recent years [Wang, Liu, Pan et al. (2016); Wang, Liu, Li et al.(2017)]. Here we directly use the overlapping community discovery algorithm to obtain the social network in the recommendation system. BIGCLAM algorithm is an overlapping community discovery algorithm for large communal network [Yang and Leskovec (2013)]. It is based on the assumption that overlapping nodes are closely connected, and it is improved from the nonnegative matrix decomposition model. The experiment in Li et al. [Li, Wu, Tang et al. (2015)] show that using the community discovering result of BIGCLAM algorithm as constraint, the recommender system can obtain better recommendation results. Here we choose BIGCLAM algorithm to discover overlapping community in the user’s social network.

User’s interests among different communities are not the same. In Li et al. [Li, Wu, Tang et al. (2015)] they use average of all users’ score vector in user-scoring matrix as community score vector. The similarity of the user’s rating vector corresponding to the community score vector of the user in the community is represented as the degree of user’s interest to the community. However, the contribution of each user to the community is different. Compared to users at the edge of the community structure, users who have more friends and direct social relationships are more representative to the community. Based on this hypothesis, we use the score vector of all users and the number of community friends to obtain the weighted community score vector.

Here, Ω(i) represents all users in community i; friendi(g) represents user ui’s direct social friends in community i;represents user score vector. According to Eq. (1),users who have more direct social relationships contribute more to the community score vector. Then, we calculate the Pearson correlation coefficient of the community score vector and the user score vector to obtain the similarity between them.

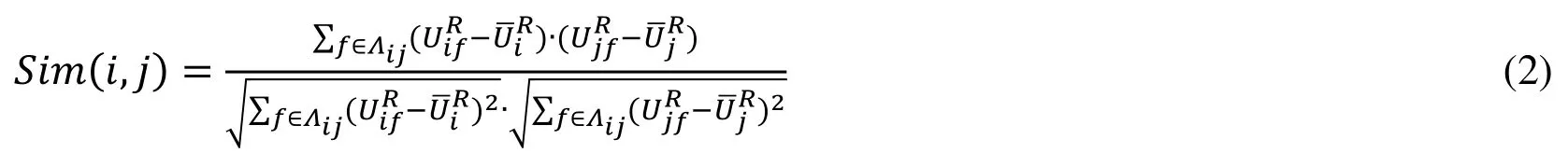
Where Aijis non-zero collections of user score vector. The output range of Pearson correlation coefficients are [-1, 1]. Here we use functionf(x)=(x+1)/2to map the output range to [0, 1].

Thus, we get the user community information based on the social network structure. The similarity between the user score vector and the community-rating vector of the community represents the user’s interest to the community.

3.3 Clustering based on interest preference

The overlapping community discovery algorithm divide users according to social network structure, and usually users belonging to the same community have similar characteristics or mutual influence. However, users in the same community may still have different preferences. For example, although those who love science fiction movies are grouped into one community, they may have different favor in music, game, travelling and so on. It is necessary to sub-group users in the same social network community. So, a fuzzy clustering algorithm based on interest preference is proposed. The algorithm utilizes the user's behavior record and the category of the project to find users who have similar preferences with the target user at generalization level.

3.3.1 Category distribution vector

The items that a user has rated may belong to different categories, and the user’s ratings percentage of the items in a category is proportional to one’s interest in that category. The distribution vector of the categories of all items that the user uihas rated can be described as follows:

Here，Piis the item collection that the user uihas rated;is the rated item collection by user ui, which belongs to category ck.

3.3.2 Category professional vector

In addition to the difference in the number of ratings for different categories, the more interest a user has in a category, the higher his or hers rating will be in this category. The well-known search engine algorithm, HITS, is used to calculate the user’s professionality in a category.

User’s historical behavior data is used to calculate one’s professionality. However, one always has different professionality in different categories. It is necessary to discuss one’s professionality respectively.

Here are two assumptions. First, if a user has rated a number of representative projects in a category, the user is familiar and professional with the category. Second, if a project has been rated by a lot of professional users, the project is representative in this category. So,for each category, one's professionality and project’s representativity can mutually reinforce each other.

For each category, one project’s representativity is the professionality sum of the users who has rated the project, and the user’s professionality is the representativity sum of projects that one has rated.

If User-project rating matrix is R ∈Rm×n, for categoryuser-project rating matrixis the number of projects belonging to categoryis a representation vector of the representativity of each project belonging to categoryis a professional vector representing the professionality of each user to categoryck.

For each category:

1) Initialize user professionality vector ℎkand project representatively vectorak, and make

2) From Eq. (4), we can get akand ℎk:

1) Normalize akand ℎk, to make

So, we get the professionality vector ℎkfor all users under each category. Choosing the value of specific position from each vector to form a vector, and normalizing it, we can get category professionality vector of respective specific position user.

3.3.3 Category preference vector

The user’s category preference has a positive relationship with user’s rating distribution and professionality in that category. So, we can obtain the user category preference vector through weighting operation with the same position value of category distribution vector and category professional vector.

Here Pre(i)kis user ui’s preference to categoryck. The category preference vector of all users is used as the sample data in following clustering algorithm.

3.3.4 Clustering objective function

Fuzzy C-mean clustering [Bezdek, Ehrlich and Full (1984)] is a relatively mature algorithm in fuzzy clustering analysis. It optimizes the objective function to obtain the membership grade of each sample point to a cluster, that is, the sample point can belong to multiple clusters at the same time, according to the nature of user preference in the recommendation system. Minkowski distance is always used when calculating the similarity between the sample point vector and the cluster-like center point vector in the fuzzy C-mean clustering algorithm.

When p=1, D(X,Y) is Manhattan distance. When p=2, it is Euclidean distance.

However, the user-project scoring matrix in the recommender system is sparse. Most users only score a few categories of projects, so the user category preference vector is sparse too. If we directly use Minkowski distance to calculate similarity, it might not get satisfying clustering result.

So we optimize similarity calculating method as follows:

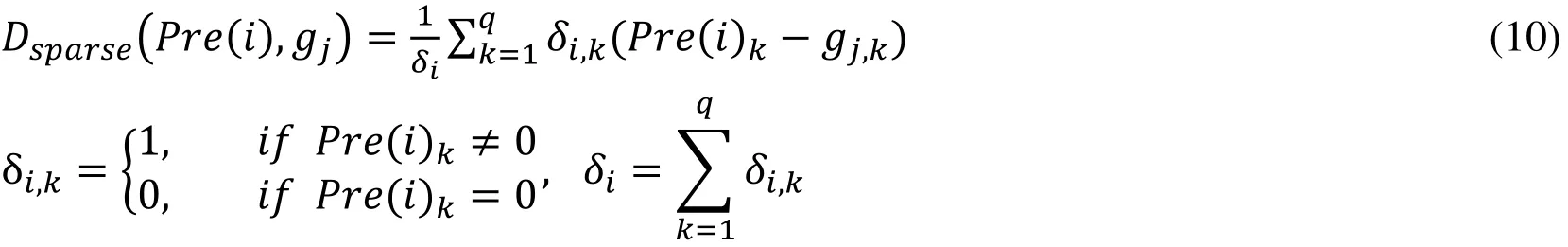
We assume the number of clusters is l. In Eq. (10), gjis the vector of a certain cluster j(j=1,2,…l). gj,kis the kth element in gj. We calculate the similarity from those non-zero elements in user category preference vector.

The objective function is defined as bellow.

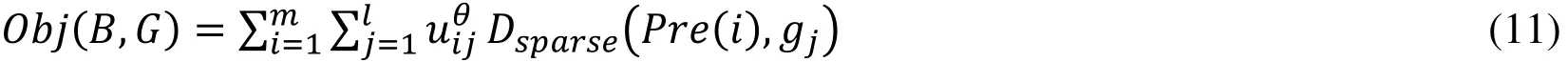
Here, uij∈ [0,1] is user ui’s membership grade to cluster ψj, and uijsatisfieswhich is user cluster membership matrix. G=(g1,g2,… ,gl)Tis cluster center matrix, and θ ∈ [0,∞] is Clustering fuzzy degree,usually it is set as 2 [Xu and Wunsch (2005)].

3.3.5 Clustering algorithm

The preference-based fuzzy clustering algorithm updates the user cluster membership matrixBand the cluster center matrixGby iteration, and approaches the objective function until the error value of the objective function converge to the preset threshold.

1) Randomly initialize the user cluster membership matrixUto satisfychoose cluster amountland clustering ambiguity θ, and determine the convergence threshold ε∈ (0,1) and maximum number of iterations tmax．

2) Update the cluster center matrixG

3) Update the cluster membership matrixB

The element uijin user cluster membership matrixBrepresents user ui’s interest degree to interest cluster ψj. Users in the same cluster have similar general preferences.

3.4 Project relevance based on comprehensive similarity

In traditional project-based collaborative filtering recommendation algorithm, the project similarity is obtained by calculating the rating similarity among common user sets in the user-project scoring matrix. However, such method requires that there are plenty of users,who have scored two items at the same time. Otherwise, we will not obtain accurate project similarity. Moreover, this approach does not take the properties of the project itself into account. Project category information is important to describe the basic information of the project. Compared with other projects, the project belonging to the same category are obviously more similar to each other. The reliability of the algorithm can be improved effectively if project category information is considered in the similarity calculation method.

3.4.1 Scoring-based project similarity

First, we obtain project similarity based on scoring by the column vector in the userproject scoring matrix. Elements in the column vector represent users’ score to that project. The scoring-based project similarity is calculated by improved Pearson correlation coefficient. We add user activity constraint in Pearson correlation coefficient calculating.

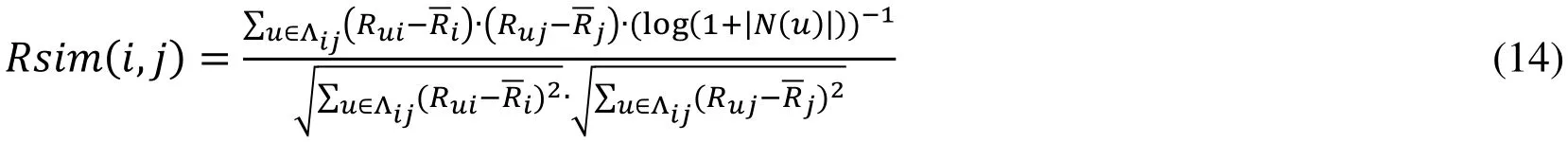
Here, Λijrepresents the position set where all elements in both project rating Riand Rjare not zero,urepresents the user who has rated projectiandj,N(u)represents the rated project set by useru. We can usef(x)=(x+1)/2to map the output to [0,1]. From Eq. (14),it is obvious that the higher the user activity is, the less the user can contribute to the project similarity.

3.4.2 Category-based project similarity

Usually many projects in the recommender system belong to multiple categories. The project can be presented as a vector of Boolean values on the category dimension, and each Boolean value reflects the project category information. We assumed that the more projects are included in one category, the greater generality the category is, and the less similarity the included projects have. The category-based project similarity is calculated using improved cosine similarity, which bases on the category generality. Thus, a category generality constraint is added to the cosine similarity.

Here,Crepresents category collection, and δicis a Boolean, if project j belongs to categoryc, then δic=1, else δic=0. N(C) represent project collection in categoryc,andN(all)represents all project collection. Formula (15) shows that the greater generality a project is, the less it could contribute to the project category similarity.

We choose the larger one from scoring-based project similarity and category-based project similarity. After normalization, project relevance based on comprehensive similarity is obtained.

Considering about computational complexity, only top 100 projects with the highest similarity to each project are recorded.

3.5 Matrix decomposition method based on entity relation decomposition

3.5.1 Probability matrix decomposition model

Matrix decomposition model is widely used in collaborative filtering recommendation algorithms. It decomposes the user-project scoring matrixRinto two low-dimensional matrix products.

Where U ∈ ℝk×m, V∈ ℝk×n, k ≪ min(m,n). The forecast score user uigives to project vjis the transpose of the ith column in low-dimensional matrixU,, multiples by the jth column inV, Vj. So, Uiis called as user implicit feature vector and Vjas project implicit feature vector. The PMF model is also decomposing user-project score matrixRinto the product of user implicit feature vectorUand project implicit feature vectorV.User’s number ismand project’s number isn, which is R ∈ ℝm×n, U ∈ ℝk×m, V∈ℝk×n, k≪ min(m,n). Assume that the conditional distribution probability of the observable data in the score matrix is as following:

Here, N(x|u,σ2)represents the probability density function of the Gaussian distribution with meanuand variance σ2.is an instruction function. If useruihas scored projectvj,then

The implicit feature matrix of both the user and the project satisfy the Gaussian transcendental with a mean of zero.

3.5.2 Matrix decomposition method based on entity relation decomposition

In fact, friends influence one’s consumption choice and users are more willing to believe their friends recommendations. The relationship between projects also impact on user consumption decision. Users are usually more interested in the project that is similar to his favor ones. A matrix decomposition model based on entity relation decomposition is proposed. The model uses the user social matrixTand the project similarity matrixS,and optimizes the implicit feature matrix of these two entities with joint decomposition of the scoring matrixR.

The improved matrix decomposition model is shown in Fig. 2. The user social relations matrixTcharacterizes the information between users. Like SoRec model, we decompose T into user implicit feature matrixUand social relationship implicit feature matrixP,where P ∈ ℝk×m. In addition, the project similarity matrixSrepresents relationship between projects, and it can be decomposed into project implicit feature matrixVand similarity implicit feature matrixQ, where Q ∈ ℝk×n.

Figure 2: Entities relationship based matrix factorization model

Suppose the user social relations matrixTand the project similarity matrixShave the following conditional distribution probability:

Suppose that social relationship implicit feature matrixPand similarity implicit feature matrixQalso satisfy the Gaussian priori with the mean equals zero.

So, we can join user rating information, user social relations and project similarity together through the shared implicit feature space. Using Bayesian derivation, we can obtain joint posterior probability distribution of matrixU, V, P, Q.

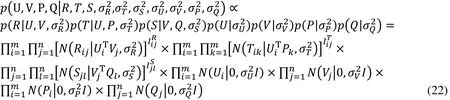
In order to maximize the joint posterior probability distribution, we take logarithm of above equation.

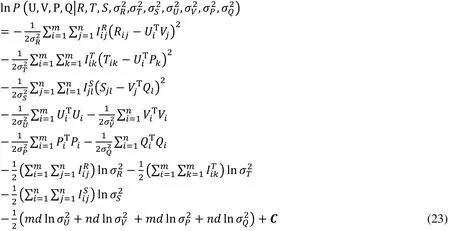
Here,Cis a constant that does not depend on the model parameters. To maximize posteriori probability of U,V,P,Q is equivalent to minimize the following error square and objective functions.

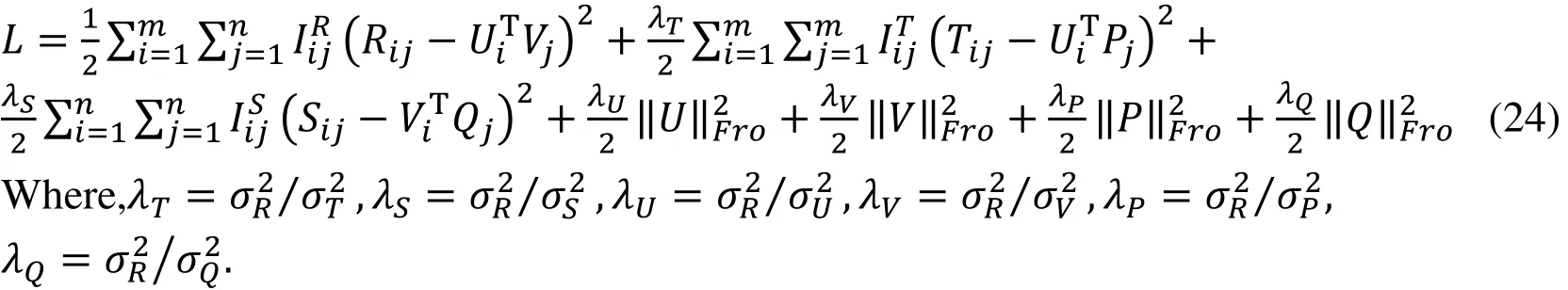
So, a matrix decomposition model based on entity relation decomposition is obtained.

3.5.3 Regularization terms based on double clustering

In real life, the decisions we make are often influenced by friends or domain authorities.In Sections 3.2 and 3.3, we get the user social network community clustering information and user generalization interest preference clustering information. The former gathers together users who interact with each other and who have the same characteristics. The latter gathers together users who have similar interest preference in multi-domain. It is clear that the similarity of the target user with the user in the same set is higher than that of the user with who does not share any of the sets. Besides, the user’s interest preference is close to the average interest preference of all the users in the same set. And the user interest degree in different sets is different. Based on the above assumptions, we improve the matrix decomposition model proposed in Ma et al. [Ma, Zhou, Liu et al. (2011)] and introduce new regular items.

Here, λZ(λZ＞0) is the coefficient of adjusting clustering regularization.is an instruction function. If useruiis in the community Υℎ(ℎ=1,2,…,cn), thenelserepresent userui’s interest degree to communityis also an instruction function. If useruiis in interest preference clusterrepresents userui’s interest degree to interest preference cluster Ψg. Ωℎ,g(i)represents the user collection who are in the same social networking community Υℎand the same interest preference cluster Ψgas userui. At this point, a regular term based on user double clustering is obtained.

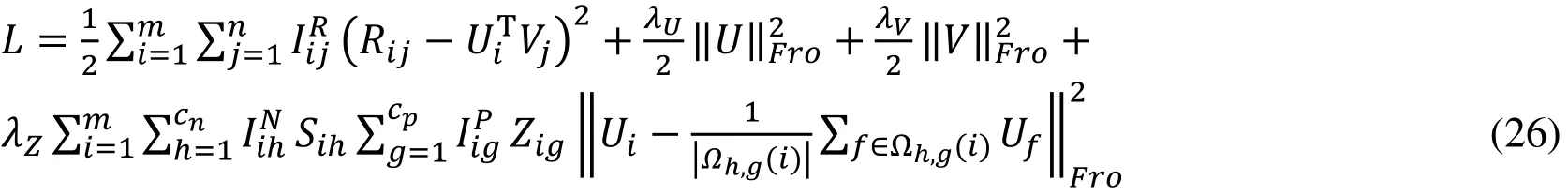
3.5.4 Entity-Association-based matrix factorization

We add the user double clustering regular term into the matrix decomposition model based on entity relation, and get the final matrix decomposition model, Entity-Association-based Matrix Factorization (EAMF). The objective function is shown in Eq. (27).

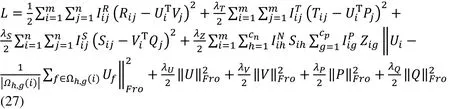
The local optimal solution of user implicit feature matrixUand project implicit feature matrixVare obtained by stochastic gradient descent method. The corresponding partial derivative is shown in Eq. (28).

The elements inUandVare updated along the gradient descending direction through iterations.

4 Experiments and evaluation

4.1 Data set

Yelp.com is one of the largest local business review sites in the world. It not only allows users to review or rate merchants, but also is an Internet company with distinguished social characteristics. It encourages active interaction between users, and a user can create a two-way confirmation of friendship with other users. The dataset we use to test the proposed algorithm is provided by Yelp. The dataset consists of 84,541 users, 43,252 items, 918,617 project scores and 725,603 two-way friend relationship information.Among them, the project score is an integer from 1 to 5, and all projects are divided into 12 categories. Detail information of the dataset is shown in Tab. 1.

4.2 Contrast algorithm

In order to verify the accuracy difference between the proposed algorithm and other algorithms, we choose the following algorithms as contrast algorithms.

BaseMF: Basic matrix decomposition model proposed in Bobadilla et al. [Bobadilla,Ortega, Hernando et al. (2013)], which does not add user social relationship information or project category information.

SocialMF: Matrix decomposition model combining user trust relationship information proposed in Jamali et al. [Jamali and Ester (2010)]. It assumes that the user vector is determined by his friends’ user vector. And the concept of trust propagation is introduced into the decomposition optimization process.

SoReg: The concept of socialized regularity is first added into matrix decomposition model in Ma et al. [Ma, Zhou, Liu et al. (2011)]. So, the user’s preference is similar to the average of his friends.

MFC: Overlapping community discovery algorithm is added into matrix decomposition model in Li et al. [Li, Wu, Tang et al. (2015)]. It distinguishes community difference on the basis of SoReg algorithm.

CircleCon: In Yang et al. [Yang, Steck and Liu (2012)], it is assumed that one’s trust to his friends is different according to different category. They divide the user trust network via project category on the basis of the SocialMF algorithm.

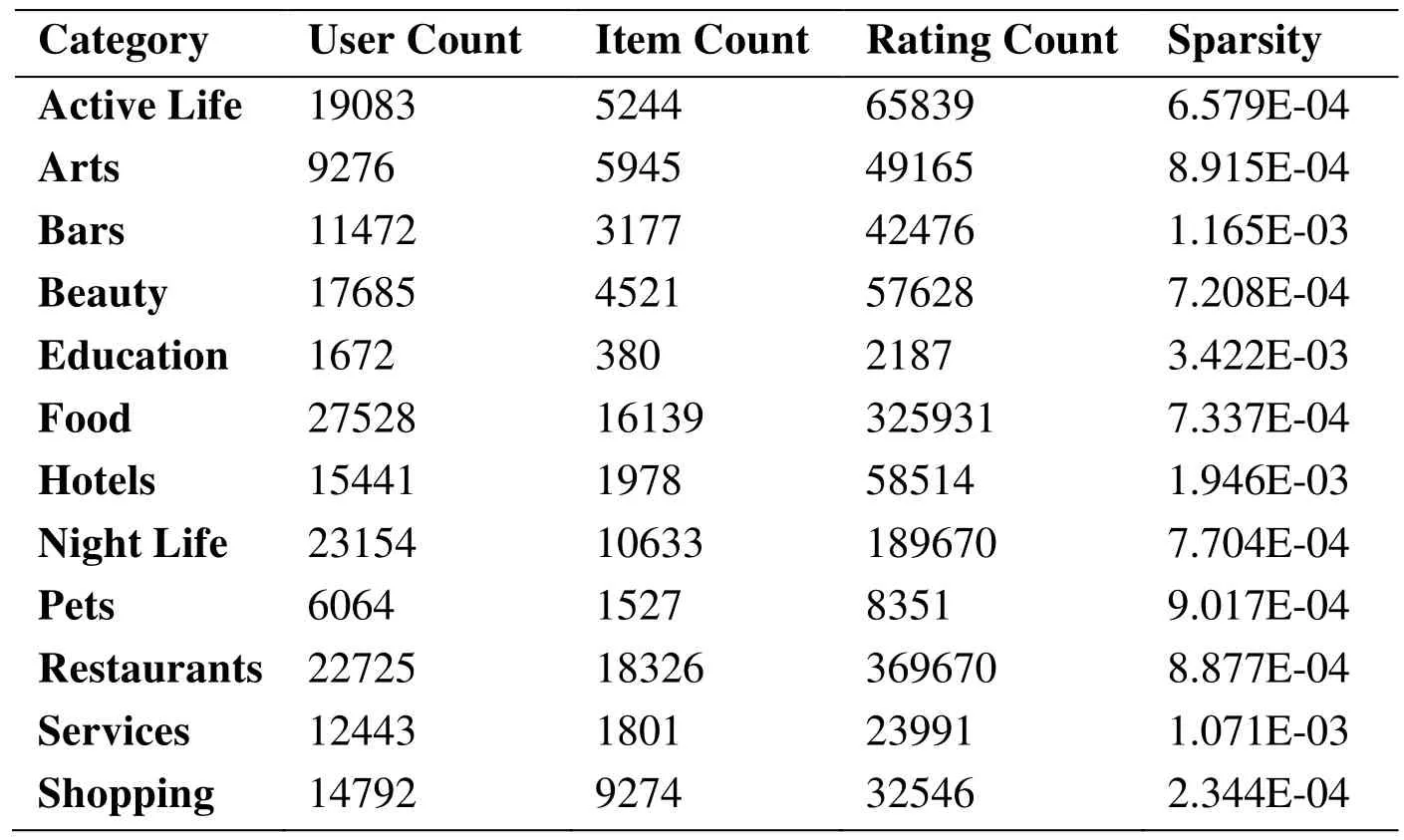
Table 1: Configuration of nodes

4.3 Evaluation index

Here we use five cross validation method. The data set is randomly divided into five parts.In each experiment, four of them are selected as a training set and the remaining one is a test set. The final evaluation data is the average of 5 tests.

We use MAE (mean absolute error) and RMSE (root mean square error) as the evaluation criteria.

Here, Rtestrepresent all users and projects in test set. RijRij represent the real score user uigave to project vj.represent the forecast score user uiwill give to project vj. Rtest represent the number of scores in test set. The smallerMAEandRMSEare, the more accurate the recommendation is.

4.4 Experiment results and analysis

4.4.1 Determine the weighting factorλs

λsrepresent the proportion of project comprehensive similarity in matrix decomposition model, which is the recommended method dependence on project relevance. If λsequals 0, it means that the algorithm does not consider about project relevance, just like SoRec model. If λsapproaches ∞, it means that only project relevance is considered. If λsequals other values, it means that it is considered in the algorithm about association influence among user direct social relations, project similarity, and project score matrix.Here, we take λsas {0.1, 0.5, 1, 5, 10, 20, 50} and the results are shown in Fig. 3.

It can be seen in Fig. 3, that λsinfluents the recommendation accuracy greatly. If λsis small, MAE and RMSE are high, which means low accuracy. As λsincreasing, MAE and RMSE gradually increase correspondingly. It indicates that project-related information plays a positive role. When λsis 5, the best result is obtained. After that the accuracy reduces again. The reason may be that excessive consideration of project relevance influence to results leads to the decrease of implicit eigenvector proportion in score matrix decomposition.

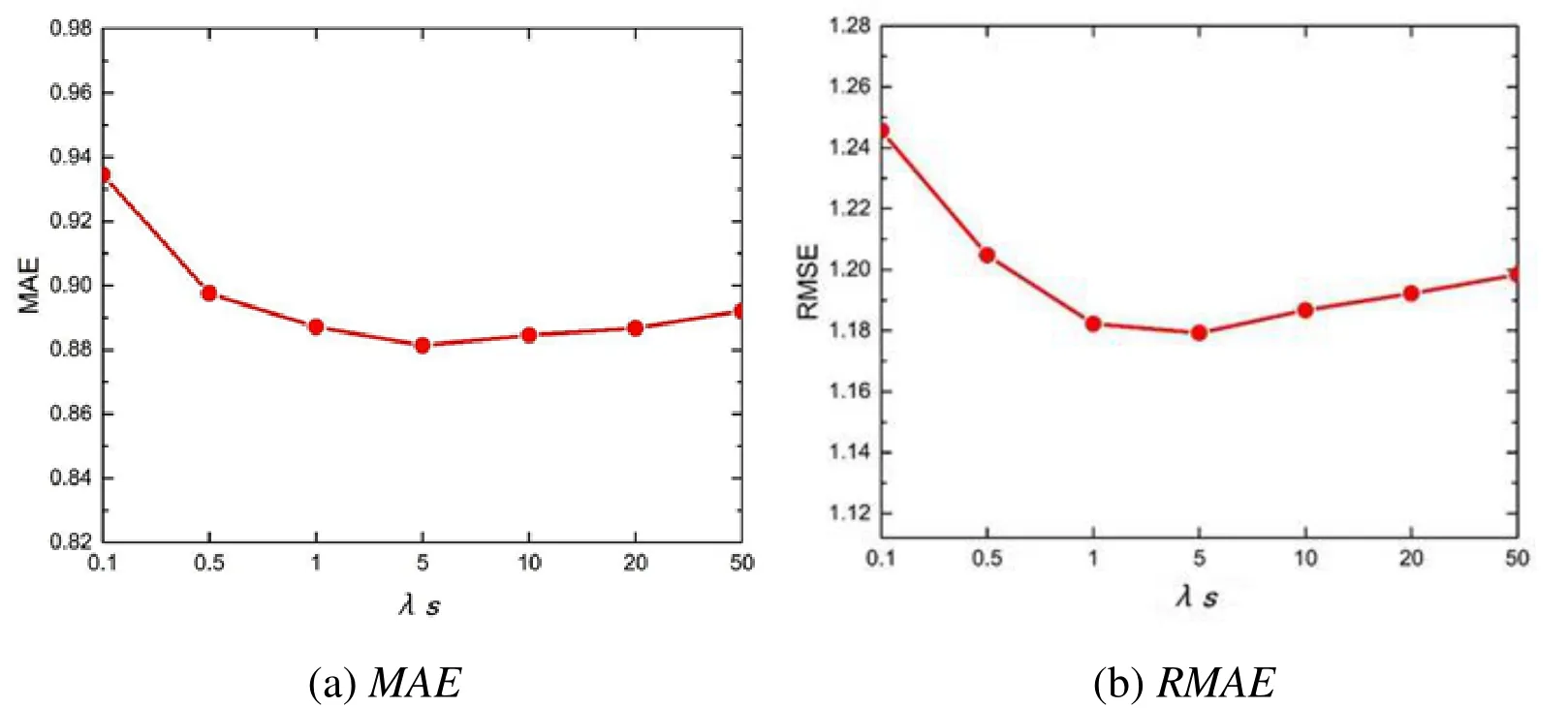
Figure 3: Impact of parameter λs

4.4.2 Determine the number of interest cluster l

lrepresents the number of generalized interest clusters that are divided by all users’behavior records and project category information. Here, we chooselfrom 5 to 25 with Step 5 and recordMAEandRMSEwith differentl. In order to understand the impact oflon the recommended results, we take five groups of experiments with different regular term coefficient λZ. The results are shown in Fig. 4.

It can be seen from Fig. 3, for different λZ, the accuracy is nearly the same with differentl. Iflis too large or too small, it will have a negative impact on the recommended results.Whenlis 15, MAE and RMSE are minimal at the same time. Iflis too small, the fuzzy clustering results cannot clearly distinguish users at different levels of interest. Similarly,iflis too large, there will be too many clusters, which may weaken the expression of user’s general interest.

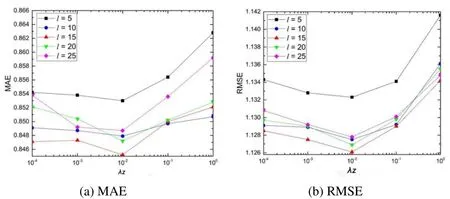
Figure 4: Impact of parameter l

4.4.3 Determine regular term coefficientλZ

λZrepresent the proportion of user social network overlapping community information and the interest preference fuzzy clustering information in matrix decomposition model.When λZis 0, the proposed model is equivalent to the basic matrix decomposition model.Take the value of λZas {0.0001,0.001,0.01,0.1,1}, and record MAE and RMSE with different λZ. Similarly, we took five group of experiments with differentlto show λZ’s influence in recommendation. The result is shown in Fig. 5.

Figure 5: Impact of parameter λZ

As can be seen from Fig. 4, for differentl, the accuracy is almost the same with different λZ. When λZis small, MAE and RMSE are relatively high. As λZincreases, MAE and RMSE decrease. The optimal accuracy is achieved when λZis 0.01. After that, the accuracy reduces again.

We think it is concerned with that additional information we used in the algorithm. When λZis too small, the additional information has little effect to obtain better user implicit eigenvector. Likewise, when λZis too large, the additional information effect too great in vector optimization.

4.4.4 Result comparison of different recommended algorithms

We can see that when λsis 5,lis 15 and λZis 0.01, our proposed algorithm, EAMF, can obtain the best recommendation result. Moreover, we compare EAMF algorithm with related algorithms described in Section 3.2. First, five cross validations determine the parameter of all algorithms in the experiment. Both regular term coefficients λUand λVare 0.01, and the dimension of user and project implicit eigenvector is 10. In SocialMF,SoReg, MFC, CircleCon algorithm, social regular coefficient λZis set as 0.01, 0.01,0.001, 0.01. β in SoReg algorithm is set as 0.5. The results are shown in Tab. 2.

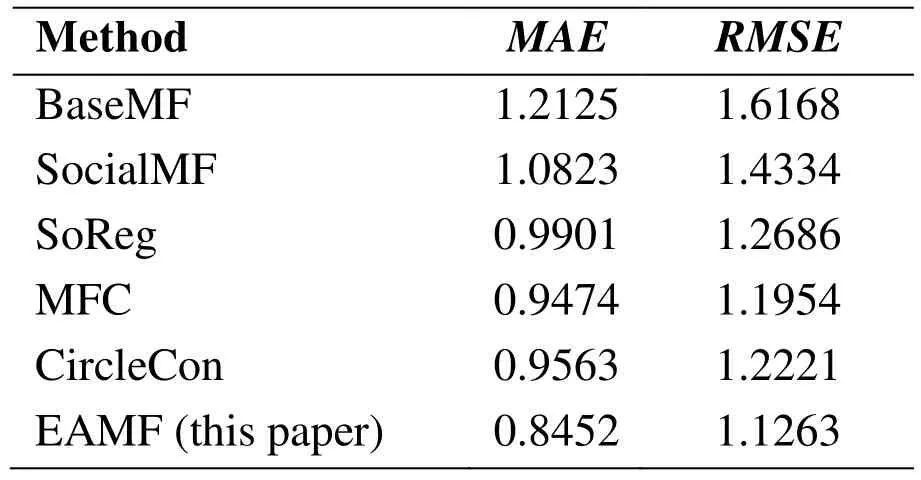
Table 2: Comparisons of EAMF and other methods

We can find from Tab. 2, EAMF algorithm, proposed in this paper, is more accurate than other algorithms. The result of BaseMF algorithm is worst because it only takes userproject scoring into account. SocialMF, SoReg, MFC algorithms do not simultaneously use user social information and project category information. The CircleCon algorithm directly divides the user by projects which are rated, while the user social relationship under a single project category may be sparse. EAMF algorithm model take project relevance as an influencing factor that is as important as user relevance, and optimizes the measurement of user relevance in the above-mentioned socialized recommendation algorithms. Therefore, it gets better recommended results.

5 Conclusion

Most traditional socialization recommendation algorithms just base on direct social relations which face with the problem of sparse social information. Because they do not take into account the impact of user interest preferences, those algorithms lead to high MAE and RMSE. Moreover, most algorithms only focus on user’s characters while ignoring that project attribute is also important in item rating.

We propose an Entity-Association-based Matrix Factorization recommendation algorithm which fuses user information and project information together. It clusters users by social relations and interest preference respectively, characterizes projects by user’s rating history and project category information, and combine the project feature matrix with user clustering matrix to predict user ratings. Experiment shows that considering the project feature, we can get better recommended results.

Acknowledgement:This work was supported by the National Natural Science Foundation of China (61772337, 61472248 and U1736207), the SJTU-Shanghai Songheng Content Analysis Joint Lab, and program of Shanghai Technology Research Leader (Grant No. 16XD1424400).