Using Imbalanced Triangle Synthetic Data for Machine Learning Anomaly Detection

Menghua Luo , Ke Wang Zhiping Cai , Anfeng Liu, Yangyang Li and Chak Fong Cheang

Abstract: The extreme imbalanced data problem is the core issue in anomaly detection.The amount of abnormal data is so small that we cannot get adequate information to analyze it. The mainstream methods focus on taking fully advantages of the normal data,of which the discrimination method is that the data not belonging to normal data distribution is the anomaly. From the view of data science, we concentrate on the abnormal data and generate artificial abnormal samples by machine learning method. In this kind of technologies, Synthetic Minority Over-sampling Technique and its improved algorithms are representative milestones, which generate synthetic examples randomly in selected line segments. In our work, we break the limitation of line segment and propose an Imbalanced Triangle Synthetic Data method. In theory, our method covers a wider range. In experiment with real world data, our method performs better than the SMOTE and its meliorations.

Keywords: Anomaly detection, imbalanced data, synthetic data, machine learning.

1 Introduction

Anomaly detection is to discover the abnormal data patterns not following the normal data behavior, in which the abnormal data is also called outlier, stain, inconsistent point or novelty depending on the application field. In our paper, we do not make a distinction between them. Anomaly detection is widely used in many fields, such as fraud detection[Zhang and He (2017); Anderka, Priesterjahn and Priesterjahn (2014)], disease detection[Pham, Nguyen, Dutkiewicz et al. (2017); Jansson, Medvedev, Axelson et al. (2015)],intrusion detection [Jabez and Axelson (2015); Kim, Lee and Kim (2014)], identification system [Huang, Zhu ,Wu et al. (2016); Ibidunmoye and Elmroth (2015)] and fault diagnosis [Dong, Liu and Zhang (2017); Purarjomandlangrudi, Ghapanchi and Esmalifalak (2014)]. In all these application fields, the abnormal data contains very important information. For instance, the fraud behavior of credit card always leads to economic loss. The abnormal data from the Internet in the intrusion detection may imply the sensitive information leakage from the attacked host. Hence, it is of great significance to improve the effect of anomaly detection.

There are mainly three kinds of approaches to solve the anomaly detection problems. The first one is the statistical model [Kourtis, Xilouris, Gardikis et al. (2017); Harada,Yamagata, Mizuno et al. (2017); Han, Jin, Kang et al. (2015)]. This kind of model needs to select the measure set describing the subject behaviors. Then build the detecting model based on the normal data. Next, choose an evaluation algorithm to calculate the distance between the current subject behavior and the detection model. At last, decide whether the behavior is an anomaly by some kind of decision-making strategy. This method can learn subject behavior adaptively. But if the adaptivity is exploited by the intruders, the anomaly may be treated as normal behaviors by the detecting model. The measure set is always assumed to be conformed to the Normal Distribution or Poisson Distribution,which is not in conformity with the real situation. The second method is the prediction model [Pang, Liu, Liao et al. (2015); Andrysiak, Ukasz, Chora et al. (2014); Pallotta,Vespe and Bryan (2013)]. In this method, the detected object is usually the time series of the events. If there is a big difference between the actual events and the prediction results,it shows that there is an anomaly. The low quality time series patterns are gradually excluded and the high quality ones are left through layers of screening. It is adaptable to the changes in the detected behavior and detects the anomaly that cannot be detected by the statistical model. The third approach is the detecting model based on machine learning [Kulkarni, Pino, French et al. (2016); Bosman, Liotta, Iacca et al. (2014)]. In recent years, these methods become more and more popular. The most significant character is to detect the anomaly by the normal data. Without too much hypothesis, the methods are widely applied in various areas. In all these approaches, the deep learning[Erfani, Rajasegarar, Karunasekera et al. (2016); Li, Wu and Du (2017)] method attracts much attention due to its powerful fitting ability. However, the number selection of the layers and units is mainly dependent on engineering experience and lack of theoretical guidance, which leads to its poor interpretability. The parameters calculation and adjustment need amounts of computing resources to support, which limits its universal extension.

For all the methods mentioned above, the relative large number of normal data plays a leading role. To get higher anomaly detection rate, complex similarity measure, lots of priori knowledge or artificially set thresholds are introduced, by which the false positive rate has been raised as well. In our work, we jump out of this way of thinking and turn to utilize the limited number of abnormal data. In the angle of data science, anomaly detection belongs to the imbalanced data problems. In the imbalanced data problems, the technique focusing on minority samples is called over-sampling, in which the Synthetic Minority Over-sampling Technique (SMOTE) and its improved algorithms have become the present standard. The artificial examples are generated randomly in the selected line segment in SMOTE and its meliorations. In this paper, we propose a new generating technology, the Imbalanced Triangle Synthetic Data (ITSD) method, breaks through the limitation range of the line segment. In our work, the SMOTE and its mainly improvements are treated as the baselines. With real world data of different domains, our ITSD method performs better than the baselines in both precision and recall. And there is a relatively balanced effect on normal data and abnormal data.

This paper is organized as follows. Section 2 briefly reviews the related works.Imbalanced Triangle Synthetic Data method is specified in Section 3. In Section 4, we describe experimental results and analysis in detail. Finally, we make a conclusion in Section 5.

2 Related work

From the view of imbalanced data problems, the normal data of anomaly detection is called the majority samples while the anomaly is the minority sample. In order to balance the imbalanced data, there are two basic ideas: one is reducing the number of the majority samples; the other is increasing the minority samples. We summarize the relevant works from these two aspects.

From the perspective of majority samples, the extraction of representative samples is the main work, called under-sampling [Lu, Li and Chu (2017)]. Two common specific methods are Ensemble method [Ren, Cao, Li et al. (2017)] and Cascade method[Kotsiantis (2011)]. The former trains N classifiers parallelly to vote the final result. The latter one is a serial method, which keeps the incorrectly classified majority samples and puts them into the next classifier training. These methods work on the balance of the data,but the extraction makes information missing more or less.

To the minority samples, the expansion of minority samples is the core target, named over-sampling. The duplicated samples method is simple, also called the randomly oversampling, with which a preliminary attempt still has a certain effect on some data sets.The Synthetic Minority Over-sampling Technique (SMOTE) [Chawla, Bowyer, Hall et al.(2002); Gutié rrez, Lastra, Bení tez et al. (2017)] is a standard of the existing methods,which randomly generates artificial examples on a selected line segment. Due to its influence, kinds of improvement algorithms emerged in the past years. SMOTE Boost[Chawla, Lazarevic, Hall et al. (2003)] integrates SMOTE and boosting together.Borderline-SMOTE [Han, Wang and Mao (2005)] divides the minority samples into three groups, DANGER, SAFE and NOISE, where different groups have their own generating ways. ADASYN [He, Bai, Garcia et al. (2008)] is an important improvement of SMOTE,which generates the synthetic examples by the proportion of the majority ratio. SVMSMOTE [Nguyen, Cooper and Kamei (2011); Wang, Luo, Huang et al. (2017)] generates artificial support vectors by SMOTE and gets good experimental results. Although these algorithms have different generating tricks, the core generating method is still the selected line segment way. To break through this generating method is our key task.

Besides, there are some methods focusing on adjusting themselves to adapt the specific application requirement. Cost sensitive method [Krawczyk and Skryjomski (2017); Roy and Rossi (2017); Li, Zhang, Zhang et al. (2018)] introduces a cost matrix with domain knowledge to adjust the imbalanced data weights. In some applications, feature selection[Moayedikia, Ong, Boo et al. (2017); Bektas, Ibrikci and Özcan (2017)] helps to improve the recognition rate of the minority. One-class classification method [Krawczyk, Woniak and Herrera (2015)] tries its best to shrink the boundary of the majority examples without considering the minority samples distribution. To a certain type of applications, it may be an effective way. But the promotion effects particularly depend on the characteristics of the dataset or domain knowledge.

In our research, we aim to maximize the use of the existing data, both the majority and the minority. We propose an Imbalanced Triangle Synthetic Data method to go beyond the existing artificial examples generating method, which has a good universality.

3 Imbalanced triangle synthetic data method

In this section, we first introduce the Imbalanced Triangle. Then, on this basis, we describe our generating method in detail. The whole process makes the Imbalanced Triangle Synthetic Data Method (ITSD).

3.1 Imbalanced triangle

In the data space, the majority samples and the minority samples are separated by the hyperplane which is called the classification hyperplane in machine learning, as shown in Fig. 1(a). From both sides of the hyperplane, we take three data points to form a triangle which we name it the Imbalanced Triangle, as shown in Fig. 1(b).

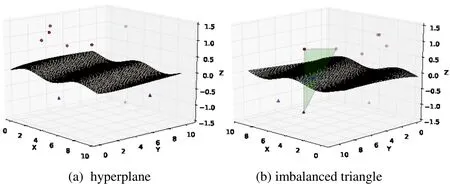
Figure 1: The imbalanced triangle passing through the hyperplane

We assume that there are n points on one side of the hyperplane and m points on the other side. There areImbalanced Triangles in all. The abundance of quantity brings theoretical advantages to our generating method. The process of proof is as follows.

Proof.Imbalanced Trianglevs.SMOTE line segment in amount

m+n≥3 To make sure the existence of the triangle.

n≥1 are the number of minority samples.

m＞n are the number of majority samples.

Ntriis the number of Imbalanced Triangles:

Nlineis the number of line segments in SMOTE:

Ntri-Nline=

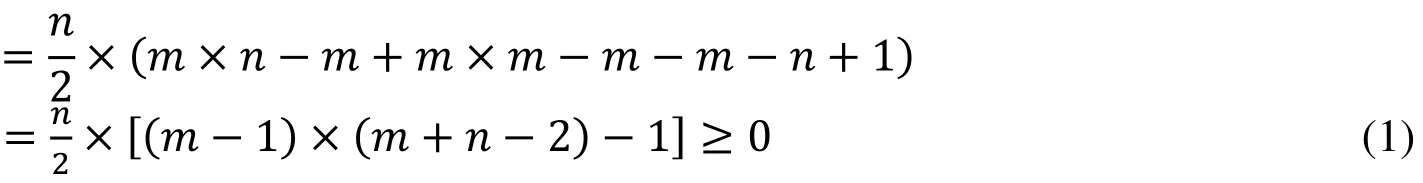
There is an important character of the Imbalanced Triangle: The Imbalanced Triangle must be intersected with the hyperplane and the intersection line is a classification line. In another simple word, there must be a classification line in the Imbalanced Triangle. This character inspires our generating method: If the synthetic examples are generated in the Imbalanced Triangle, we can make all these artificial samples as the minority by controlling the classification line.

In anomaly detection, the data distribution is usually extremely imbalanced (m＞＞n).This problem, in our Imbalanced Triangle, is just an advantage. In Imbalanced Triangle,the vertexes are the given original data points, the edges are from the SMOTE line segments and the whole area corresponds to the space between the majority and the minority. The generating method of SMOTE based algorithms selecting only edges means to neglect the most space. To maximum the minority data information, we select the whole area as the generating space of the synthetic minority examples. From Eq. (1),we can infer that if we reduce m in a reasonable range, our Imbalanced Triangle still has more numbers than the SMOTE line segments in theory.

3.2 The ITSD generating method

The generating method is the core of the over-sampling synthetic technology. We compare the present methods and adjust them as the basis of our method.

In SMOTE and its improved algorithm, the generation process almost uses Eq. (2). It randomly picks up xj, one of the k nearest neighbors of the selected minority sample xi,and then generate artificial sample xgwith Eq. (2), where λ∈(0,1). In simple words, xgis selected randomly on the line segment (xi,xj). In SMOTE-borderline2, the parameter λ is adjusted (λ∈ (0,0.5)) to make the generated examples close to the minority sample xi.

In data explanation, we interpret Eq. (2) as adding disturbances or noises, as Eq. (3).Obviously, thehere is the key point of the algorithm design. In other words, Eq.(2) is a specific form of Eq. (3).

In our generating method, to break through the limitation of Eq. (2) and Eq. (3), we propose our Imbalanced Triangle formula in Eq. [eq:tri]. First we find the top k nearest neighbors of each example in minority class. Then synthetic samples are generated by the formula in Eq. (4), where random numbers α, β, τ and ς ∈ (0,1), instead of the SMOTE generating method in Eq. (2). Hereis the generated example, andare three points in the k nearest neighbors. Especially,is the selected minority example itself, andhas to be the first majority example in the k neighbors, whereis another point in the top k. This method generating the synthetic samples in a triangle range determined byis a fixed vertex and the other two vertexes are random points in line segmentsIn simple words, there are two steps in our generating method: The first one is to select a sub triangle of the Imbalanced Triangle; the second step is to generate a random point in the triangle of the first step. To simplify the problem, we may set α =1 and β =1, which means the range is the whole Imbalanced Triangle

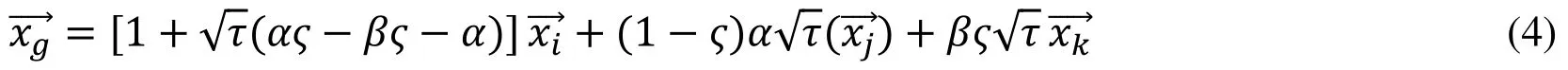
Proof.Derivation Process of Eq. (4)

Comparing the classic generative method in SMOTE and its improved algorithms, our generative approach is more efficient. All the Imbalanced Triangles cover more areas where the minority samples may appear than the line segments in old methods, which reflects the characteristics of the minority data distribution better. What is more, the fixed minority example vertex and its nearest majority point make a bigger probability of the artificial example generating between the hyperplane and the minority samples than the pure random way. After obtaining the synthetic samples closing to the data distribution,we mix the synthetic examples and the minority samples together as the extended abnormal data. According to the specific anomaly detection application requirement, we can transform the extremely imbalanced data problems to common imbalanced problems or relative balance supervised learning. After this transformation, the anomaly detection problem is easy to deal with by a machine learning classification method. In this section,we clarify the Imbalanced Triangle Synthetic Data method and analyze its theoretical advantages comparing to the existing approaches. Its good performances dealing with real world data are shown in the next section.

4 Experiment and result

In this section, the empirical analysis of our method is stated. We make comparisons with seven baseline approaches, using five real world data sets of different anomaly detection fields.

4.1 Data sets

We use five datasets from the UCI open data2http://archive.ics.uci.edu/ml/index.phpto examine our ideas. German Credit (GM)dataset3http://archive.ics.uci.edu/ml/datasets/Statlog+%28German+Credit+Data%29is from the fraud detection, which has 1,000 instances and 20 attributes. The original data has 700 majority samples and 300 minority samples. We adjust the imbalanced rate to 450:50 in the training set.

Haberman’s Survival (HM) dataset4http://archive.ics.uci.edu/ml/datasets/Haberman%27s+Survivalis from the disease detection, which contains 306 instances and 3 attributes. The original data has 225 majority samples and 81 minority samples. We adjust the imbalanced rate to 170:25 in the training set.

Breast Cancer Wisconsin Original (BCW) dataset5http://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+%28Original%29is also from the disease detection,which records 699 instances and 10 attributes. With the missing values removed, the original data has 444 majority samples and 239 minority samples. We adjust the imbalanced rate to 220:15 in the training set.

The Pima Indians Diabetes (PID)6http://archive.ics.uci.edu/ml/datasets/Pima+Indians+Diabetesis another dataset from the disease detection, which has 768 instances and 8 attributes. The original data has 500 majority samples and 268 minority samples. We adjust the imbalanced rate to 250:20 in the training set.

Spambase (SB) dataset7http://archive.ics.uci.edu/ml/datasets/Spambaseis from the identification system, which collects 4,601 instances and 57 attributes. The original data has 2,788 majority samples and 1,813 minority samples. We adjust the imbalanced rate to 1000:25 in the training set.

4.2 Experimental settings

We choose seven approaches in our experiment as the baselines: the original imbalanced data without preprocessing, random over-sampling (ROS), SMOTE, SMOTE-SVM,SMOTE-borderline 1, SMOTE-borderline 2 and ADASYN.

In anomaly detection evaluation, the anomalies and the normal data should be separated.We calculate the f1-scores of the majority and the minority respectively, in order to compare the balanced effects of the algorithms for imbalanced data.

To verify the universality of the algorithms, we select four commonly used classifiers with different principles: Decision Tree (DT), Logistic Regression (LR), Support Vector Machine (SVM) and Naive Bayes (NB).

Figure 2: The experiment results

4.3 Experimental results and discussions

In order to adapt to the requirements of abnormal detection, we set the training set as extremely imbalanced as possible. Using ITSD and the seven baseline methods, we respectively evaluate the F1-Scores of the minority examples (anomalies) and the majority samples (normal data) with the four classifiers mentioned above. The experiment results are shown in Fig. 2. In all the five datasets, our ITSD method and the other seven approaches have steady performances in DT and LR. In NB, there is a little reasonable fluctuation. But in SVM, the results are unstable and volatile. The performances of the majority are a little better than the minority. Due to the contribution of the synthetic data, the gaps are not so large as in the original extremely imbalanced data.

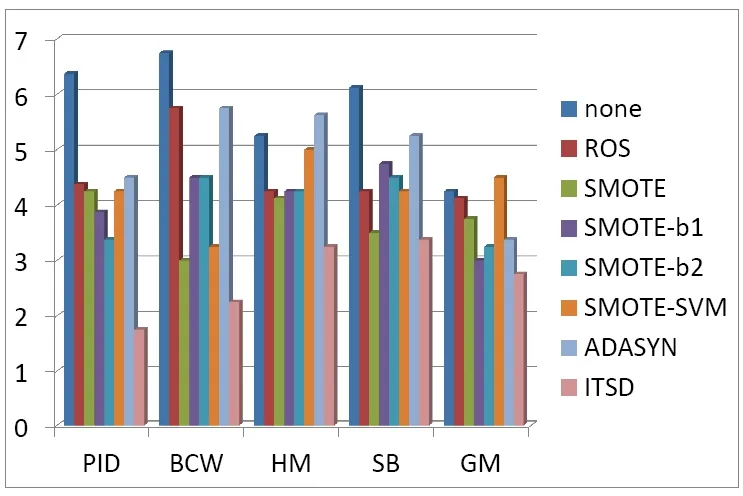
Figure 3: Ranking of all the methods

We sort all the rankings of the methods and the final ranking is shown as Fig. 3. From the figure, it can be seen that our ITSD method performs the best in all these approaches. In all the five anomaly detection datasets of different domains, the ITSD method achieves the best F1-score than the seven baselines. To the four classifiers of different theoretical basis, our approach gives the most stable performance.

5 Conclusion and future work

In this paper, we propose an Imbalanced Triangle Synthetic Data (ITSD) method to deal with the anomaly detection problems and to break through the limitation of the existing line segments generating method. We analyze its theoretical advantages in a mathematical way and use the experimental results of real world data to verify its empirical effect.Experimental results demonstrate that the ITSD method can be applied in multiple anomaly detection fields and performs relatively steadily under different classifiers. In following work, we aim to study the correlations between the abnormal data and the normal samples in the extremely imbalanced anomaly detection problems.

Acknowledgement:This research was financially supported by the National Natural Science Foundation of China (Grant No. 61379145) and the Joint Funds of CETC (GrantNo. 20166141B020101).