一种基于DCS-KF的高移动稀疏信道估计方法

袁伟娜， 王嘉璇

(华东理工大学 信息科学与工程学院， 上海 200237)

信道估计技术是无线通信技术中的重要环节，其准确与否直接影响到通信系统的整体性能，研究信道估计技术具有重要的意义。在快速移动的环境中，如高速铁路等场景，信号频率会产生多普勒效应，使得在1个符号周期内信道将快速变化，这样大大增加了需要估计的信道参数的数量。对此，文献[1-3]研究了基于小波基和基扩展模型(Basic Expansion Model, BEM)的时变信道模型，该模型可以较好地拟合快时变信道特性，降低了待估计参数数量。文献[4]对每个正交频分复用(Orthogonal Frequency Division Multiplexing ,OFDM)符号块对应的快时变信道分别进行BEM建模，采用最小二乘(Least Squared, LS)和线性最小均方差(Linearly Minimum Mean Square Error, LMMSE)对BEM系数进行估计。文献[5]考虑了信道的时域相关性，采用卡尔曼滤波(Kalman Filter, KF)对相邻符号对应的BEM信道模型系数进行估计，获得信道估计。而在郊区、山区等信道环境，信道多径是由几个具有明显响应值的主径和大部分响应值近似为零的径组成，即信道多径时延分布是零散的。如果仍然采用传统方法，系统性能会降低。文献[6-10]研究了基于压缩感知(Compress Sensing, CS)算法的稀疏时不变和时变信道估计问题。文献[11]中针对单个符号内信道响应不变而相邻符号间变化的慢时变稀疏信道，采用KF与CS相结合的算法进行信道估计。分布式压缩感知(Distributed Compress Sensing, DCS)[12-13]是CS的扩展，对于具有联合稀疏性的信号组可以实现一次联合重构。文献[14]基于DCS研究了时不变稀疏的多入多出正交频分复用(Multiple Input Multiple Output Orthogonal Frequency Division Multiplexing, MIMO-OFDM)系统信道估计。

上述文献仅考虑了信道的某一个或两个特性进行研究，本文同时考虑了符号间相关性、信道的快时变性和稀疏特性，提出了一种联合KF和DCS信道估计的新方法。

1 系统模型

采用BEM基模型，信道响应表示为

( 1 )

式中：n=0,1,…,N-1，N定义为采样总点数;l=0,1,…,L-1，L定义为在最大时延内的总径数。在1个OFDM符号周期内，用h(n,l)表示第n个采样点第l径的信道响应；bq(n)为BEM基函数；gq(l)为BEM的系数；Q为BEM的阶数。一般地，在一个OFDM符号内，BEM系数是不变的。由于基函数由一组固定的正交基组成，所以待估计的参数数量由N×L个降到(Q+1)×L个。一般情况下Q远小于N，因此大大的降低了待估计的参数数量。

式( 1 )的BEM公式写成矩阵形式为

( 2 )

式中：bq=[bq(0),bq(1),…,bq(N-1)]T;Gq为N×N维的Toeplitz循环矩阵；h为N×N维的时域信道矩阵。

( 3 )

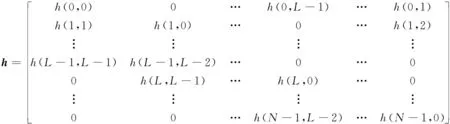
( 4 )

假设系统已同步，去除循环前缀(Cyclic Prefix,CP)后，OFDM系统的时域接收信号为

( 5 )

式中：x，y分别为发送与接收的信号；w(n)为均值0，方差为σ2的加性高斯白噪的第n个采样点；( )N定义模为N的循环移位。

式( 5 )写成矩阵形式为

y=hx+w

( 6 )

式中：

y=[y(0),y(1),…,y(N-1)]T

x=[x(0),x(1),…,x(N-1)]T

w=[w(0),w(1),…,w(N-1)]T

则相应的频域接收信号为

Y=FhFHX+W=HX+W

( 7 )

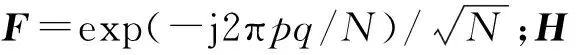
将式( 2 )带入式( 7 )有

( 8 )

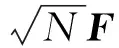
令Aq=Fdiag(bq)FH，式( 8 )可以表示为

( 9 )

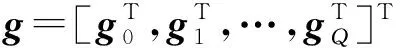
Y=AΔg+W

(10)

再令S=AΔ，那么频域接收信号可最终为

Y=Sg+W

(11)

2 基于DCS-KF的快时变稀疏信道估计

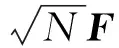
本文采用CS估计稀疏信道主径位置时，需要先建立CS的观测方程。在基于梳状导频的OFDM系统中，1个符号周期内的子载波数为N，导频符号数为NP，第p个导频符号在整个子载波的位置为Pp，p=0,1,…,NP-1。如果将发送端所有导频信号为XP，那么相应的接收端信号YP可为

YP=HPXP+WP

(12)

式中：XP，YP为NP×1维的向量；WP是NP×1维的导频处噪声；HP是NP×NP维的信道频域响应，第p个导频位置处的信道频响，可为

(13)

式(13)也可以用式(14)表示

(14)

因此，在1个符号周期内，可将所有导频符号位置所对应的信道频响为

H(P)=Φh

(15)

式中:

H(P)=[H0,H1,…,HNp-1]T

h=[h0,h1,…,hL-1]T

其中，Φp,l为NP×L维的元素，Pp为第p个导频在子载波中的位置。

本文假设多个OFDM符号内多径时延保持不变，则每个信道参数具有相同的稀疏部分，符合文献[9]中介绍的适用于DCS的联合稀疏模型，因此采用DCS估计稀疏主径位置。

将第j个OFDM符号导频处的稀疏信道模型为

(16)

本文假设每个符号内导频位置相同，则每个观测矩阵也相同。由相邻J个OFDM符号组成的信号组对应的联合稀疏模型为

(17)

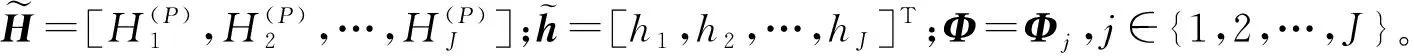
同时正交匹配追踪(Simultaneous Orthogonal Matching Pursuit，SOMP)算法是从最优匹配追踪算法(Optimal Matching Pursuit，OMP)的扩展而来，区别在于SOMP每次迭代中挑选与信号组残差最匹配的原子，建立DCS的观测方程后，基于文献[9]中模型采用DCS-SOMP重构算法估计稀疏主径位置。具体步骤为

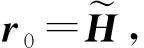
Step2最匹配原子索引为

其中,ej为单位列向量，φi为Φ第i列；

Step3更新索引集Λt=[Λt-1,λt]；

Step4计算已选原子集下信号的LS估计值为

其中,ΦΛt是Φ中与Λt对应列;

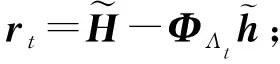
Step6如果tε，则t=t+1，重复Step1～Step5，否则迭代终止。

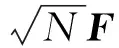
考虑到信道的时域相关性，采用KF算法估计BEM系数，进而获得信道估计值。首先，采用自回归模型(Auto Regressive, AR)[15]来表征相邻OFDM符号间信道响应随时间变化的线性平滑关系。为了降低算法复杂度，采用一阶AR模型

hm,l=Ah,lhm-1,l+um,l

(18)

式中:hm,l定义为第m个OFDM符号内第l径的信道时域响应向量;Ah,l定义为信道系数状态转移矩阵;um,l是协方差为Ul复高斯向量，表示模型误差。

hm,l的BEM模型可以写作

hm,l=Bgm,l

(19)

式中:hm,l=[hm(0,l),hm(1,l),…,hm(N-1,l)]T;gm,l=[g0(l),g1(l),…,gQ(l)]T;B=[b0,b1,…,bQ]定义为BEM基系数的矩阵;bq=[bq(0),bq(1),…,bq(N-1)]T。

对经过BEM转换后的基系数建立类似AR模型

gm,l=Ag,lgm-1,l+um,l

(20)

式中:Ag,l是BEM基系数状态转移矩阵;um,l为协方差，Ul的模型误差。通过尤尔-沃克(Yule-Walker)方程可以求得AR模型参数为

(21)

因为BEM系数是零均值的相关复高斯变量，其相关矩阵为

(BHB)-1BHRhl(s)B(BHB)-1

(22)

又由于本文采用的是Jakes模型信道，则

(23)

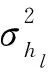
将每径的AR模型结合，可表示为

gm=Aggm-1+um

(24)

最终将式(24)看作是KF算法状态方程，将第m个符号所对应的频域接收信号(见式(11))看作是KF算法的测量方程，进一步表示为

(25)

采用KF算法进行多个OFDM符号的BEM基系数估计，具体步骤为

Step1初始化

(26)

Step2时间更新

(27)

Step3测量更新

(28)

式中:gm|m-1为参数的预测值;gm为参数的估计值;Pm为估计误差的协方差矩阵;Pm|m-1为预测估计误差的协方差矩阵。得到多个符号的BEM系数估计值后，根据BEM模型得到主径位置处信道估计值，其他位置处值近似为0。

3 实验仿真

本文基于Matlab仿真平台，对算法进行验证。仿真中，真实信道采用符合Jakes模型的Rayleigh多径衰落信道，QPSK调制，梳状导频结构，选用GCE-BEM，阶数Q=2，其余参数设置见表1。重复试验100次的平均主径位置估计准确度为

(29)

信道归一化最小均方误差为

(30)

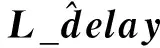
表1 仿真参数表

在归一化多普勒频移fnd=0.3(即移动速度v=450 km/h)的情况下，DCS和CS进行主径估计的准确度情况，见图1。

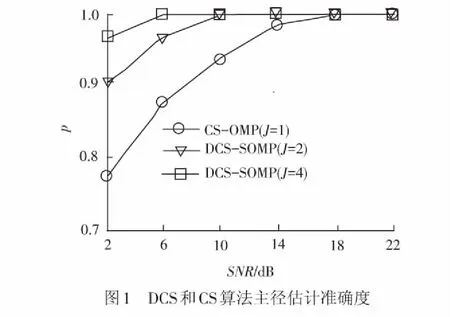
其中，CS-OMP(J=1)表示采用CS的OMP算法对单个OFDM符号进行估计，DCS-SOMP(J=2)表示采用DCS的SOMP算法对2个OFDM符号进行联合估计，DCS-SOMP(J=4)表示采用DCS的SOMP算法对4个OFDM符号进行联合估计。由图1可以看出，在信噪比SNR较低时，信道噪声干扰较大，对估计准确度有所影响。在相同的较低SNR情况下，由于使用了多符号间信道相关性，采用DCS-SOMP估计的准确度高于只针对单个符号的CS-OMP，而J=4时DCS-SOMP的估计准确度较J=2有所提高。而随着SNR的增加，信道状态变好，估计准确度增加，在较高SNR情况下，三者具有相近且较高的准确度。

不同条件下，采用DCS和CS结合KF算法进行快时变稀疏信道估计性能见图2。其中，DCS-KF表示采用DCS对主径位置估计准确度高时信道估计的性能，CS-KF表示在同等条件下采用CS对主径估计准确度低时信道估计的性能。从图2(a)可见，在信噪比SNR=15 dB时，随着fnd从0.05增加到0.3，对应于移动速度从75 km/h增加到450 km/h，载波间干扰增加，信道估计性能降低。从图2(b)可见，在fnd=0.2(即移动速度v=300 km/h)时，随着SNR增加，信道状态变好，信道估计性能有所提高。此外，结合图1可见，在DCS-KF主径估计准确度比CS-KF高的情况下，其信道估计性能也优于CS-KF。

4 结束语

针对快时变稀疏环境下OFDM系统的信道估计问题，本文提出1种信道估计的新方法。新方法同时考虑到了信道的稀疏性和信道的时变性，先采用DCS技术对主径位置进行估计，然后采用KF算法对主径位置的信道BEM基系数进行估计，进而获得了信道的估计值。通过仿真验证，该方法在快时变稀疏环境下可以提高主径估计准确度，从而提高了信道估计的性能。