二重化两电平与三电平整流器等效关系的证明

王鹏展， 李华伟， 曹天植， 王 昕， 徐建忠

(1. 北京交通大学 电气工程学院， 北京 100044; 2. 中铁电气化局集团有限公司 设计研究院，北京 100166;3. 国网冀北电力有限公司 电力科学研究院， 北京 100045； 4. 国网宁夏电力有限公司 检修公司， 宁夏 银川 750011)

牵引变流器是动车组交流传动系统的核心部件，随着高速铁路快速发展以及南、北车的合并，对牵引变流器的选择逐渐有了归一化的趋势。目前变流器网侧部分主要有两电平整流器与三电平整流器2种结构。两电平脉冲整流器结构简单，三电平脉冲整流器性能更为优良。文献[1-6]详细介绍了CRH1到CRH5型动车组的牵引传动系统，仿真分析了牵引变流器在不同工况及控制策略下的性能。目前对三电平整流器各输出特性的研究方法主要采用计算机建模仿真[6-8]，该方法不能揭示各种特性产生的机理。文献[9-10]利用双重傅里叶变换详细分析了两电平整流器网侧输出电压谐波特性，但没有涉及多重化两电平的研究。文献[11]分析了考虑死区时间的两电平整流器输入侧PWM波形，但缺乏理论与仿真的对比。文献[12]使用3D几何墙模型推导了三电平整流器交流侧电压表达式并给出了实验验证，虽然该方法能够揭示交流侧电压谐波的产生机理，但其计算过程比较复杂，且未对2种整流器的等效性进行严谨证明。文献[13-14]对三电平整流器网侧电流进行了深入研究，但没有对直流侧电压进行分析。

本文从两电平与三电平整流器的调制方式入手，在不考虑直流二次纹波影响的条件下，推导了二重化两电平整流器的开关函数，并通过计算和仿真等方法，从多个角度对2种整流器的等效关系进行了证明。说明在一定的相位关系下，二重化两电平整流器与三电平整流器开关函数，交流侧电压及其谐波分布，以及直流侧电压具有等效性。对于动车组变流器归一化问题的定量分析提供了理论支撑。

1 两电平与三电平整流器的拓扑结构

1.1 两电平脉冲整流器的主电路结构

两电平脉冲整流器主电路原理见图1[15]。其中，uN,LN,RN分别为牵引变压器二次侧额定电压、等效电感、等效电阻；iN为整流器输入电流；uab为整流器交流侧电压；Cd为直流电容；Ud为整流器直流侧电压；R为负载电阻；idc为直流侧总电流；ic为电容电流；id为负载电流。

定义2个桥臂开关函数Sa和Sb。每个桥臂上下2个开关管的驱动信号互反，使得2个开关函数均有0，1两种取值，得到整流器交流侧电压与直流侧电压的关系为[16]

uab=(Sa-Sb)Ud

( 1 )

1.2 单相三电平脉冲整流器的主电路结构

二极管钳位式单相三电平脉冲整流器主电路结构见图2。同样依据A，B 2个桥臂的开关导通关系，定义其2个桥臂的理想开关函数为SA和SB，每个桥臂上的4组开关管的开关组合使2个开关函数均有-1，0，1三种取值。其交流侧输入端的电压可表示为

( 2 )

式中：ΔU为直流侧两电容上的电压差。

图2中，C1，C2分别为直流侧电容1、电容2；U1，U2分别为直流侧电容1、电容2电压；i1，i2分别为直流侧电容1、电容2电流；o为连接点。

2 2种整流器开关函数的等效证明

2.1 两电平与三电平整流器的调制方式

两电平脉冲整流器的PWM调制中，a，b两相的三角载波相位相同，调制波反相，a相调制波大于其三角载波时，Sa为1，否则为0，b相调制过程与之类似。在三电平整流器A，B两相的调制波与载波的相位均相差180°，且载波又分为正侧载波和负侧载波。当A相的调制波大于正侧载波时，SA为1，小于负侧载波时，SA为-1，介于两者之间时SA为0。2种整流器均采用单极性调制，采样方法为自然采样法，不考虑器件死区，得到调制波形见图3。

对比2种脉冲整流器的调制过程，两电平整流器交流侧输入端开关信号波形与三电平整流器一相上的PWM开关信号波形相同，即SA=Sab，此时2种电平的调制波频率相同，而三电平PWM的载波频率为两电平PWM载波频率的2倍。显然在一定的相位关系下，可以通过2个两电平整流器的开关函数代替单个三电平整流器的开关函数。

2.2 二重化两电平的开关函数

通过前面的分析可知，可以通过图4的两电平整流器的二重化等效1个图5的三电平整流器。二重化的2个整流器的调制波相位反相时，可以产生与三电平整流器A，B 2个桥臂相同的开关信号。

图4、图5中，uN，L，R分别为牵引变压器二次侧电压、漏感、电阻参数。其中，uN1=-uN2=uN3。

由于调制过程中，三角载波的角频率远大于调制波的角频率，因此在1个载波周期中可认为调制波的值恒定。

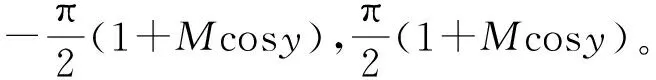
设两电平整流器a相上开关函数傅里叶级数为

( 3 )

当m=0时

a0=1+Mcosy

( 4 )

m≠0时

( 5 )

( 6 )

其中用到的雅克比-安格尔展开式为[17]

( 7 )

式中：ζ，θ为自变量；k为阶数；J0(ζ)为0阶贝塞尔函数；Jk(ζ)为k阶贝塞尔函数。

将式( 5 )、式( 7 )、式( 8 )代入式( 4 )，整理得单相两电平a相桥臂上的开关函数为[18]

cos(mx+ny)

( 8 )

式中：Jn为n阶贝塞尔函数;x=x=ωct+θc；y=ω0t+θ0。其中，θ0为调制波的初相位，θc为载波的初相位。

两电平整流器b相的调制过程与a相类似，调制波相位相差180°，推得b相桥臂的开关函数为

( 9 )

联立式( 8 )和式( 9 )，本文推得单个两电平整流器的开关函数为

Sab1(t)=Sa(t)-Sb(t)=

(10)

两电平整流器开关信号应同三电平整流器一相上的开关信号相同，故根据单相三电平整流器A，B两相调制波与载波的相位关系，得到另一个两电平整流器的开关函数为

Sab2(t)=Mcos(y-π)+

(11)

式(10)与式(11)相减，二重化两电平开关函数为

S12(t)=Sab1(t)-Sab2(t)=

(12)

式中:S12(t)为二重化两电平开关函数；Sab2(t)为另一个两电平整流器的开关函数。

2.3 二重化两电平整流器交流侧电压

假设二重化两电平整流器直流侧电压Udc为定值，不考虑直流二次纹波的影响，则其交流侧的电压为

0.5u12(t)=[Sab1(t)-Sab2(t)]Udc=UdcMcosy+

(13)

式中：u12(t)为二重化两电平整流器交流侧电压；Udc为二重化两电平整流器直流侧电压。

若令ωc=1 000π,ω0=100π，调制深度M=0.8，直流侧电压Udc为100 V。对式(13)计算可得0.5倍二重化两电平整流器交流侧电压，见图7(a)。 仿真可得单相三电平整流器交流侧电压波形，见图7(b)。

由于地理位置、开发条件和国家政策的原因，西沙群岛群岛邮轮旅游仅停靠全富岛、银屿岛和鸭公岛三座岛屿，线路单一。因全富岛、银屿岛和鸭公岛三座岛屿面积小，成熟开发的旅游产品少，游客体验好感度下降。加之西沙群岛的地理位置，极易受台风影响，邮轮旅游产业脆弱性高。

通过计算所得二重化两电平整流器交流侧电压波形与仿真所得单相三电平整流器交流侧电压波形对比发现，电压波形基本一致。只是计算波形受迭代次数限制产生了少许毛刺，但与仿真电压值的偏差在±1%之内。

对计算所得二重化两电平整流器交流侧电压与仿真所得三电平整流器交流侧电压进行谐波分析，对比了部分次数谐波含量，见表1。

表1 部分谐波含量的计算与仿真结果对比

注：谐波含量=谐波幅值/基波幅值×100%。

理论计算与仿真分析2种方式所得的谐波分布与含量基本一致，谐波含量误差在2%以内。通过网压波形与谐波特性的对比说明，二重化两电平整流器的开关函数表达式应同样适用于单相三电平整流器。

3 2种整流器交流侧电压与谐波特性等效证明

模拟整流器实际运行工况，采用瞬态电流控制。2种整流器交流侧电压均为1 500 V，直流侧目标电压为3 000 V。其中，2个两电平整流器交流侧输入电压和调制波相位均相差180°，载波相位相差为90°，载波频率为500 Hz；单相三电平整流器的载波频率为1 000 Hz。

仿真分析分别得到二重化两电平整流器和单相三电平整流器的交流侧输出电压，见图8。对图8的电压波形进行谐波特性分析，见图9。

通过对比可以看出，2种整流器仿真所得网压波形、谐波分布和谐波含量基本一致，谐波主要集中在偶次倍载波频率附近，且只含有奇数次谐波；证明了二重化两电平交流侧电压波形与谐波特性与三电平整流器相一致。

4 2种整流器直流侧电压等效证明

4.1 额定工况变为轻载时的直流侧电压

对二重化两电平整流器和单相三电平整流器的直流侧输出电压进行仿真分析。仿真初始时为额定负载，第3 s时负载减半。

仿真分析分别得到二重化两电平整流器和单相三电平整流器的直流侧输出电压,见图10。

当负载减小的瞬间，2种整流器的直流侧电压在短时间内会有轻微波动，但在反馈控制下，电压会在很短的时间内恢复成给定值并保持稳定。2种整流器在额定负载和轻载工况时均能维持稳定的直流电压。

4.2 额定工况变为过载时的直流侧电压

参数保持不变，仿真分析到3 s时，负载增加50%,见图11、图12。

在负载突然增大时，2种整流器直流侧电压虽有轻微下降，但依然能够快速恢复为给定值。由于反馈控制过程中2种整流器的PI参数选取不同，对输出结果造成一定的影响。但2种整流器均能在0.5 s内使直流侧电压达到给定值。不同的负载情况下，直流侧电压均能稳定在给定值附近，二次纹波系数约为3%，只是在负载突变瞬间会产生1 s左右的电压波动。通过以上对比验证了2种整流器直流侧电压的等效性。

5 考虑死区效应的整流器交流侧电压等效证明

在实际工作中，为了防止同一桥臂上2个功率器件出现直通现象，变流器需要设置死区时间，使器件导通时间延迟一个td，死区时间的引入使输出电压出现电压偏差。两电平整流器1个桥臂上的电压偏差为[19]

(14)

采取前文思路，通过载波移向，逐个求出每个桥臂的电压偏压，最终得到二重化两电平整流器的电压偏差为

cos[(2n+1)ω0t]

(15)

式中：Δu为二重化两电平整流器的电压偏差；fc为三角载波的频率；td为器件导通延迟时间。

考虑死区时间对二重化两电平整流器交流侧等效电压的作用，可以先忽略直流侧二次纹波的影响，然后将式(15)与式(13)相加。假设死区时间为5 μs，可得二重化两电平整流器交流侧电压，见图13。

同样设置死区时间为5 μs下，二重化两电平与三电平整理器交流侧电压仿真波形，见图14。

通过公式推导与仿真分析所得结果对比发现，考虑死区效应之后，二重化两电平与单相三电平整流器交流侧电压波形仍基本保持一致。证明在考虑死区效应时，2种整流器也是等效的。

6 结束语

本文以两电平与三电平脉冲整流器为研究对象，通过比较2种整流器的脉宽调制方式，得出二重化的两电平整流器与三电平整流器的开关信号等效关系；在此基础上，从调制中占空比变化的角度，经过傅里叶级数展开，推导出了二重化两电平整流器模型的开关函数表达式。通过理论计算与建模仿真可知，二重化两电平整流器的开关函数表达式同样适用于三电平整流器；并且对比了2种整流器的交流侧电压及其谐波分布，不同工况下的直流侧电压以及考虑死区时间后的交流侧电压波形。多角度验证了二重化两电平与三电平整流器的等效关系。鉴于二重化两电平整流器没有三电平整流器的中点电位平衡问题，不需额外的控制策略，不仅具有三电平整流器同等的功能，还略具优势，因此在本文所讨论的范围内，可以用二重化两电平整流器取代三电平整流器。