基于单子带信号重构改进算法的电机故障诊断
2019-02-22邹运
邹运
(大庆油田有限责任公司第二采油厂第五作业区地工队,黑龙江 大庆 163000)
1 问题描述
1.1 电机轴承发生故障的原因
电机的故障一般在轴承上,电机轴承会发生破损、表面剥落、压痕、磨损、裂纹、点蚀、胶合、变色以及锈蚀等多种异常现象,主要原因有异常推力载荷引起的损伤、内外环倾斜造成的损伤、落入异物造成的损伤、润滑不良造成的损伤、微小震动的影响、装配不良造成的损伤以及电蚀等。
1.2 电机轴承各元件的特征频率
滚动轴承类型以角接触型球轴承为例,假设滚道与滚动体之间为纯滚动接触,轴承中各元件均无受力变形。
滚动体缺陷的旋转特征频率:当滚动体上有一个缺陷时,每当滚动体自转一周的时候,滚动体缺陷的旋转特征频率为:
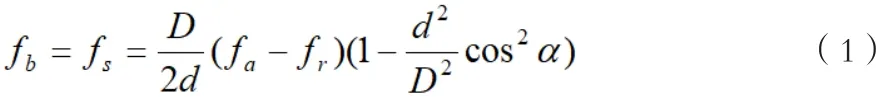
内滚道(外环)缺陷的旋转特征频率:当缺陷在内滚道上时,相对滚动体质心旋转一周,内滚道缺陷的旋转特征频率为:
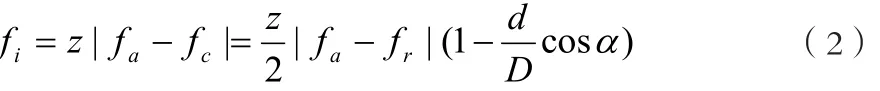
外滚到(内环)缺陷的旋转特征频率:当缺陷在外滚道上时,相对滚动体质心旋转一周,外滚道缺陷的旋转特征频率为:
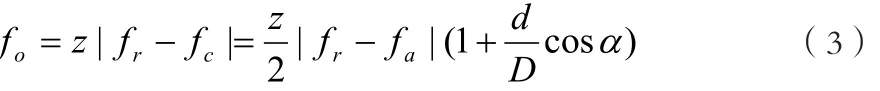
因此,当电机轴承发生故障时,都有各自的故障特征频率。
2 单子带信号重构算法
2.1 Mallat算法及频率混叠现象
离散小波变换(Mallat)算法在小波分析中与FFT在傅里叶分析中的作用类似,降低了计算量和数据量。算法为:

重构算法:
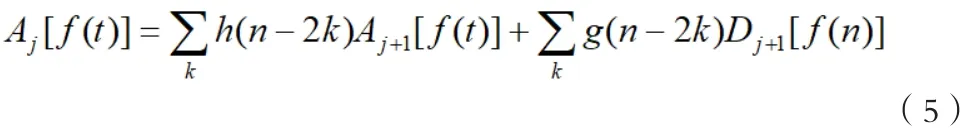
在Mallat算法中,G,H,g,h四个滤波器的关系为:
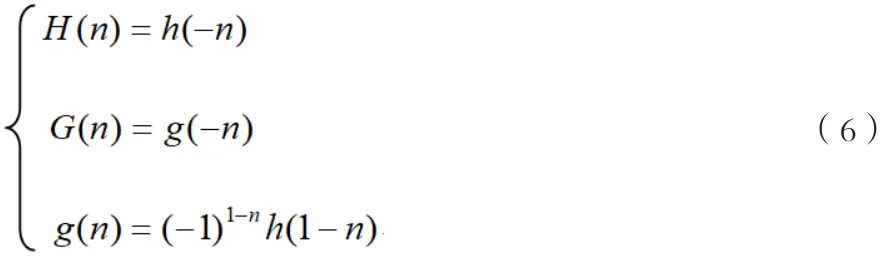
利用 Mallat 算法进行信号分解,从滤波的角度来看,是将信号的频带二进划分成一系列子带的过程。Mallat算法在这三个环节内会出现频率混叠现象。
2.2 单子带信号重构算法
虽然Mallat算法中,隔点插零与隔点采样都存在频率混叠现象,但方向相反,即在隔点采样中的频率折叠又在隔点插零中纠正了过来,如果两者同时作用,错误分量会抵消。把信号按Mallat分解算法进行分解,得到各尺度上的小波系数;然后将各子带上的小波系数分别重构至与原始信号相同的尺度。单子带重构算法是一个将信号分解到一系列二进划分频带上的过程,隔点采样中的频率折叠在隔点插零中得到纠正。所得到的子带信号与原始信号具有相同的采样频率。
3 单子带信号重构的改进算法
假设小波滤波器是理想的,由于频率折叠相反,去掉了单一子带里没用的频率成分,单子带重构信号中就没有频率混淆了。单子带重构的改进算法如图1。

图1 单子带重构改进算法
(1)算子CH、ch、CG
设x(n)为2j上低频子带小波系数,Nj为2j尺度的数据长度,W=e-j2π/Nj,则CH、ch的计算式:

其他:
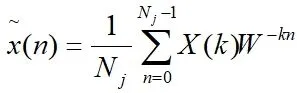
CG的计算式:

其他:
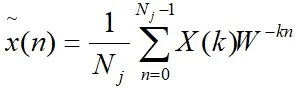
(2)在取得近似部分Aj过程中,消除频率混淆的方法
②把快速傅里叶变换结果中频率比fs/2j+1大的谱值设为零;
③将置零后的值做IFFT;
④把IFFT的值隔点采样,将结果Aj做下一步分解。
(3)在取得细节部分Dj过程中,消除频率混淆的方法
①Aj-1与g卷积后,用表示,对快速傅里叶变换;
②把FFT结果中f ≤fs/2j+1的频谱值设为零;
③将置零后的值IFFT,结果Dj不再隔点采样。
(4)在自近似部分Aj单子带重构过程中,消除频率混淆的方法
在2j上,没有被隔点采样的信号进行重构,不进行隔点插零,而是在第2j-1上进行隔点插零。在开始的重构中没有虚假频率成分,后来产生的虚假成分会被h滤掉,便消除了Aj重构过程的频率混淆。
(5)在自细节部分Dj单子带重构过程中,消除频率混淆的方法
①设Dj重构的结果是dj,将dj快速傅里叶变换;
②把FFT中非[fs/2j+1,fs/2j]的部分谱值设为零;
③把置零后的值IFFT,所得值即为准确的dj。
4 实验结果分析
用傅里叶变换处理故障信号的结果如下:

图2 用傅里叶变化处理故障信号运行结果
如图2所示,轴承润滑状态不良时引起的轴频振动能量占了绝对优势,很难分辨出其他的频率成分。
用基于小波的常规单子带信号重构算法和改进的单子带信号重构算法对故障信号进行处理,选用db10为基本小波,将信号分解至三层,其结果分别如图3、4所示。
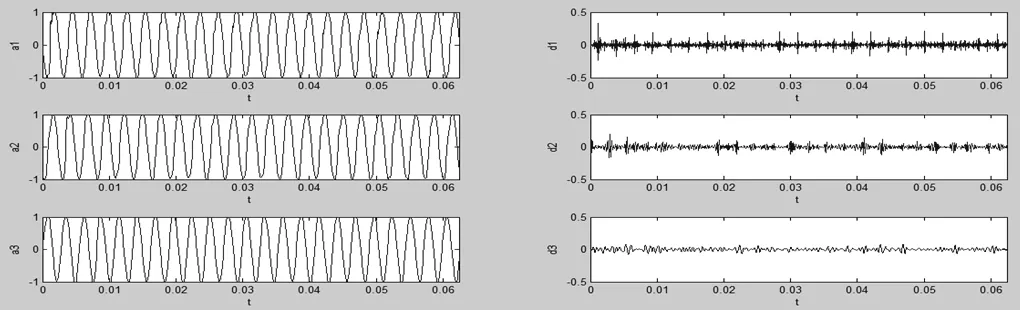
图3 用常规算法处理故障信号运行结果
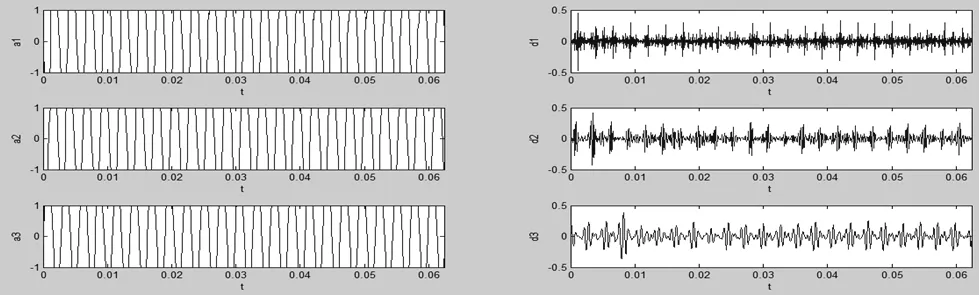
图4 改进算法处理故障信号运行结果
如上图可清楚地看到故障冲击特性,除了轴承润滑状态不良,还存在其他故障。再比较两图中的d2,会发现隐约有一点瞬态冲击的迹象。
并发现子带d2中明显有等间距的冲击存在,在时间上与d1同步。证明改进的单子带信号重构算法与常规算法相比,信号处理效果更好。
冲 击 信 号 时 间 为 0.002727, 则 频 率 为,非常接近理论频率368Hz,可诊断为电机的滚动轴承外环发生了故障。
5 结语
上述实验中,本文利用快速傅里叶变换(FFT)和快速傅里叶逆变换(IFFT)的改进算法对各子带信号处理,能够准确地提取出隐含的以及较微弱的初期故障信号特征,有效的克服了信号分解与重构时的频率混叠问题。
