几种公建能耗异常数据修正方法的比较
2019-02-22王蕊
王 蕊
(杭州市城市建设科学研究院,浙江 杭州 310003)
公共建筑能耗是建筑能耗的重要组成部分,“十二五”期间我国建筑能耗总量呈现持续增长趋势,据《中国建筑能耗研究报告(2017)》统计,截止到2015年,全国建筑能耗8.57亿t标准煤,其中公共建筑能耗2.92亿t标准煤,占建筑能耗总量的34%。随着互联网的发展及大数据时代的到来,“用数据说话”来进行能耗管理成为必然。然而,现实生活中,由于公共建筑功能复杂、数据传输系统、配电设备寿命、环境多变等因素的影响,往往导致能耗监测平台收集的数据不准确,甚至缺失,这就使得能耗监测平台难以发挥相应的作用。
为了解决上述问题,我们需要对能耗监测平台采集的数据进行甄别、补充。本文以杭州市建筑节能信息管理平台为数据来源,比较分析几种能耗异常数据的修正方法,并通过实验检验几种能耗异常数据修正方法的有效性、准确性。
1 能耗异常数据修正方法概述
能耗监测平台不仅可以用于观测公共建筑当前能耗消耗情况,还可以通过历史能耗数据综合分析公共建筑的用能特点,实现节能管理,所以保证高质量的能耗监测数据十分必要。但是,现实生活中由于各种外界因素的干扰,采集到的能耗监测数据往往不能达到所需要求。数据异常主要存在三种问题:1)数据丢失,由于传输信号中断导致的“0”数据或空数据问题;2)数据错误,由于差分的计量方式导致的数据极值或负值问题;3)数据不平衡,由于计量设备配备不齐全导致的能耗监测数据超高问题[1]。
为了提高能耗监测数据质量,需要剔除异常数据并补充合理的预测值,目前有很多基于数据统计的智能算法用于缺失值的补充,如SVD算法、聚类算法、模糊理论、多元回归预测分析等,但这类算法需要大量的有效历史数据进行训练,建立准确的数学模型来预测。而公共建筑实时能耗监测数据并不完整,用复杂算法对单一变量(电能)进行研究,难以建立准确的数学模型,且算法计算时间长。
本文选取了三种能耗监测异常数据修正的方法,并通过实验分析比较三种方法对公共建筑能耗异常数据修正的有效性、准确性。
1.1 一阶差分法
一阶差分法是较为常见的剔除异常数据的方法,它认为当系统的采样频率符合奈奎斯特采样定理时,相邻两个采样点间的数值相差不大[2],即
xt-1-xt-2=xt-xt-1
因此,可以通过t-1时刻和t-2时刻的值对t时刻的能耗值进行预测,即
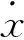
1.2 最大阈值法
能耗数据变化规律具有相似性、周期性,因此短期内相似日的能耗数据变化应维持在一定范围内[3],如果某一时刻能耗检测值超出这一范围,则认定为异常值剔除。最大阈值公式如下:
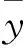
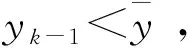
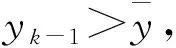
综上所述,最大阈值法只考虑异常时刻前的能耗值,可以满足能耗监测数据当日修正的要求,从而提高监测数据质量。
1.3 MkNNI算法
1968年Cover和Hart提出了KNN算法的概念(图1),因其思路简单、易于实现、准确度较高的特点,常被用于数据分类[4],随着人们对KNN算法的不断改进,其应用范围也越来越广泛,并在人脸识别、文字识别、医学图像处理等领域取得了较好的效果[5]。同时,KNN算法也是常见的数据填补方法,其计算过程如下[6-7]:
1)构建数据矩阵Z(包含缺失项);
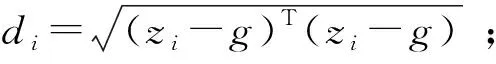
3)选取k个di最小的数据作为目标数据的最近邻;
4)计算目标数据的最近邻加权系数
5)计算最近邻加权平均值填充缺失值

但是,在公建能耗数据中存在一类不同于上述异常数据的值,他们并非异常,但不符合公共建筑能耗变化的客观规律,这类数据通常定义为噪声。如果KNN算法选取的最近邻包含噪声数据,则会影响填充数据的精度,所以文献[8]提出了一种相互最近邻算法——MkNNI算法,实现缺失数据和最近邻完全数据的相互k最近邻,有效解决了存在噪声的问题。给定完全数据集T和参数k,x的相互k最近邻数据为:
Mk(x)={xi∈T/xi∈Nk(x)∩x∈Nk(xi)}
其中,Nk(x)是x的k最近邻数据集。
《企业会计准则》重新制定关于企业内部研发费用的会计处理,批准其符合标准可资本化。促进了无形资产的会计处理和信息披露的标准化。然而,实际运用中,行业标准缺乏标准型和统一性,企业往往依赖主观判断和内部未来计划标准去进行实际会计操作,研发支出费用化或资本化不仅从一方面可说明企业会计处理的谨慎性,其装化为无形资产可调整利润,无形中提高了市场乃至社会对于相关信息的披露要求。

图1 MkNNI算法说明图
例如,图1中x的k=3最近邻为x1、x2、x3,同样的x1、x2、x3的k=3的最近邻分别是{x,x2,x7}、{x,x1,x7}、{x4,x5,x6}。最终得到x的相互k=3最近邻为{x1、x2}。
用MATLAB实现MkNNI算法的伪代码如下:
1 能耗数据规范化;
2 While (循环次数为当月天数)
3 目标数据与基础数据逐条计算欧式距离;
4 End
5 从完全数据集中得到目标数据的k个最近邻Nk(x);
6 For 每个最近邻y∈Nk(x)
添加到Mk(x)中 ;
8 If (Mk(x)≠ø))
9 用Mk(x)中每条数据的加权平均值填充目标数据;
10 Else
11 用KNN算法填充目标数据
12 End
2 实验结果分析
杭州市城市建筑能耗监测平台是对区域内建筑能耗的总体管理和分析,主要为政府建筑节能管理服务[9]。本文选取杭州五洋宾馆2017年9月的能耗监测数据来检验以上三种能耗异常数据修正方法的效果,并用RMSE评价指标衡量准确率,计算公式如下:
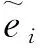
图2是杭州五洋宾馆2017年9月的逐时能耗监测数据,可以看出能耗监测数据的变化呈明显的周期性和相似性。在实际工况中,能耗异常数据包括“0”数据或恒定数据、单点数据异常、连续时刻数据异常,下面本文主要针对后面两种异常情况进行数据验证,其中,异常时刻数据剔除后用“0”代替计算。
1)单点数据异常
我们选取杭州五洋宾馆2017年9月21日0时至23时的能耗监测数据为目标数据,随机剔除4个时刻的数据为异常点,见表1。
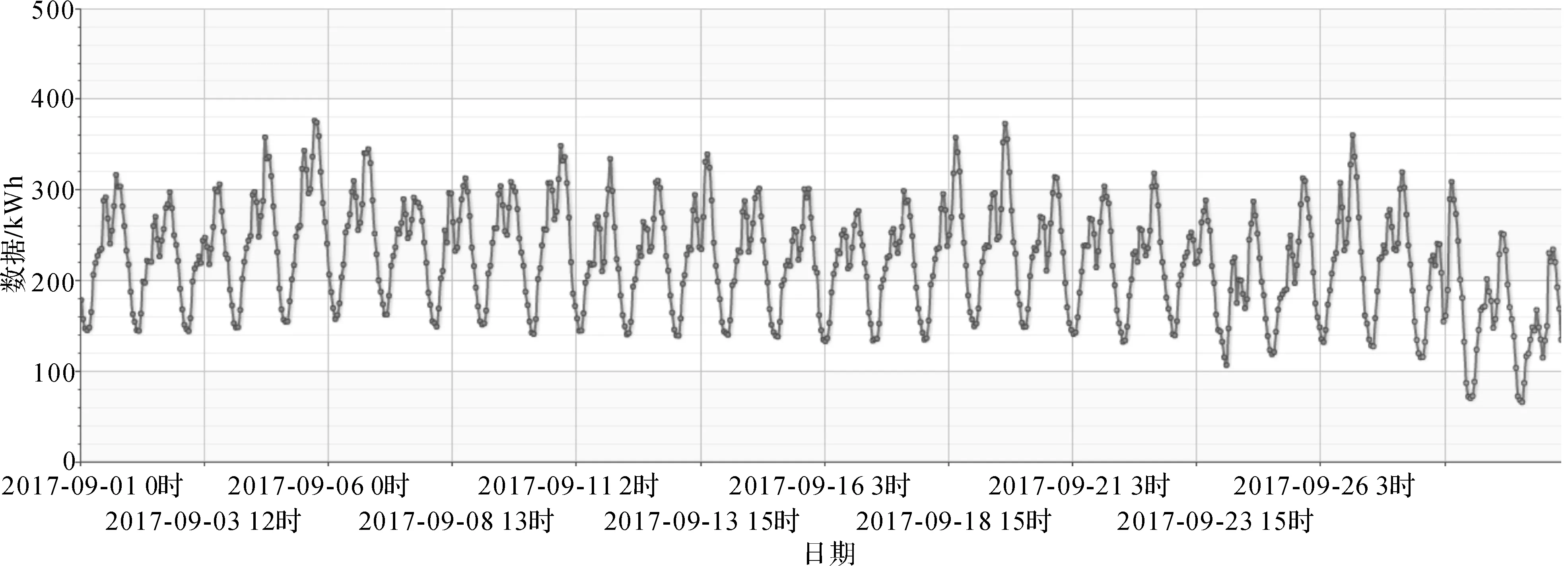
图2 杭州五洋宾馆2017年9月逐时能耗监测数据

时刻0时1时2时3时4时5时6时7时8时9时10时11时能耗值17015314514101591872100239238268时刻12时13时14时15时16时17时18时19时20时21时22时23时能耗值26725121502642900292285254216195
分别用MkNNI法、一阶差分法、最大阈值法对异常点的数据进行修正填充,得到结果见表2。通过计算三种修正方法的均根方差RMSE值可以看出,MkNNI算法的修正结果远远好于一阶差分法和最大阈值法。图3反映了三种方法修正数据逼近原数据的情况。其中,最大阈值法在异常时刻的修正值远远大于实际监测值,误差偏大,修正效果不理想;一阶差分法在数据变化拐点处,修正值的变化趋势与实际值相反,如在15时由于数据变化趋势反向导致修正值远远小于实际监测值,修正效果较差;MkNNI算法在各个异常时刻的修正值均在实际监测值附近浮动,且变化趋势与原数据一致,误差小,修正效果较好。
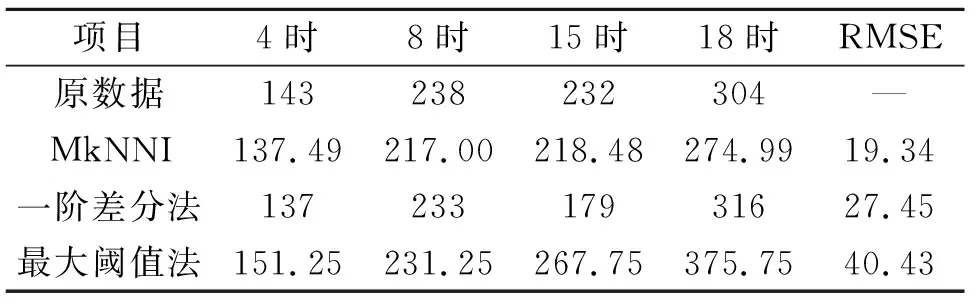
表2 三种方法修正单点异常数据结果及RMSE值
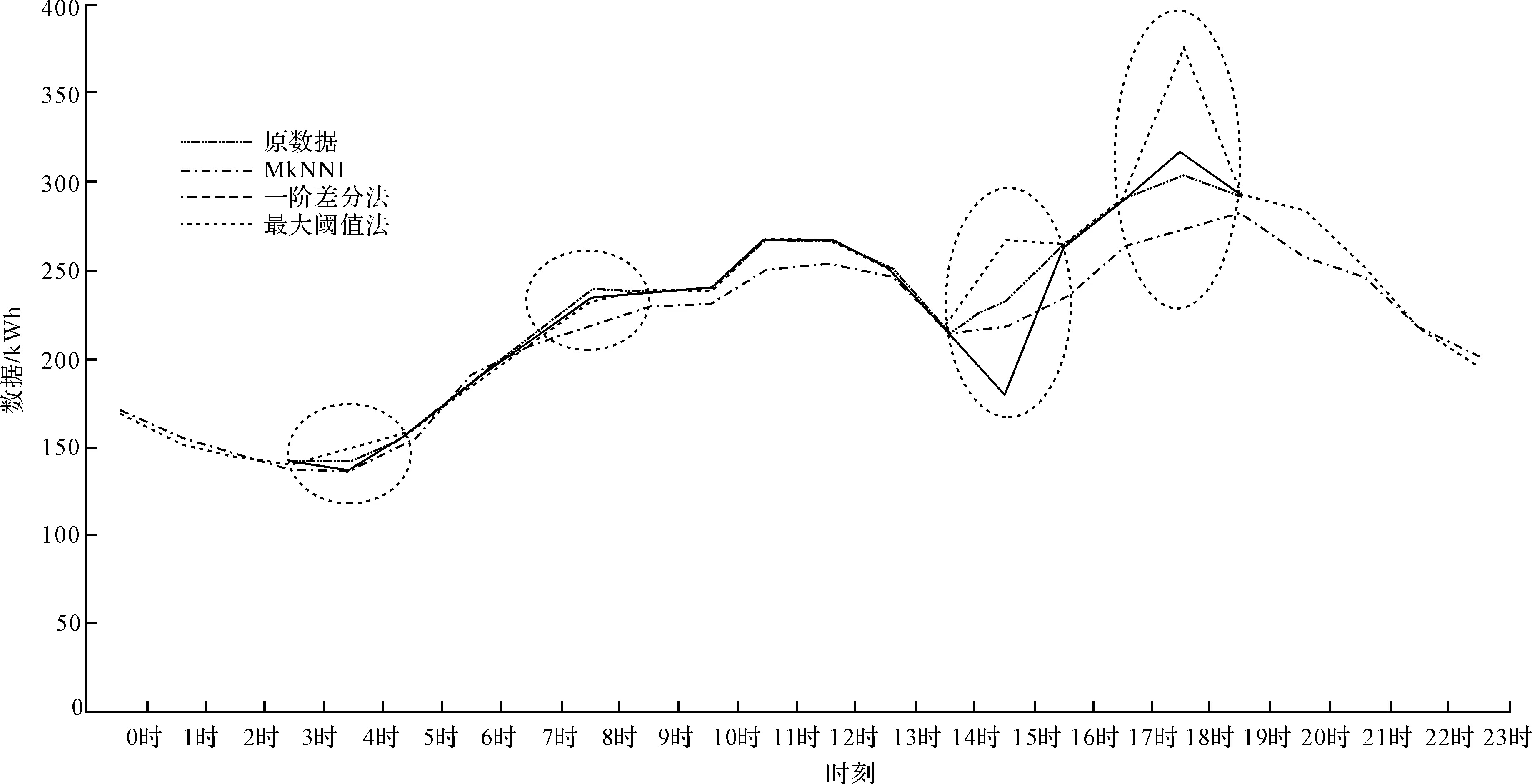
图3 单点数据异常情况下三种方法修正结果对比图
2)连续时刻数据异常
我们选取杭州五洋宾馆2017年9月27日0时至23时的能耗监测数据为目标数据,随机剔除8个连续时刻的数据为异常点,见表3。

表3 含连续时刻数据异常能耗监测数据表
通过三种方法得到的异常值修正结果见表4,从均根方差RMSE来看,MkNNI算法依然是修正效果最好的。而图4也反映出,MkNNI算法最逼近实际监测值;一阶差分法明显在连续时刻数据异常的情况下,无法预测数据变化趋势,且在14时修正数据与实际变化趋势相反,修正值失真;最大阈值法得到的所有修正值均偏大于实际监测值,修正效果均不理想。

表4 三种方法修正连续时刻数据异常结果及RMSE值
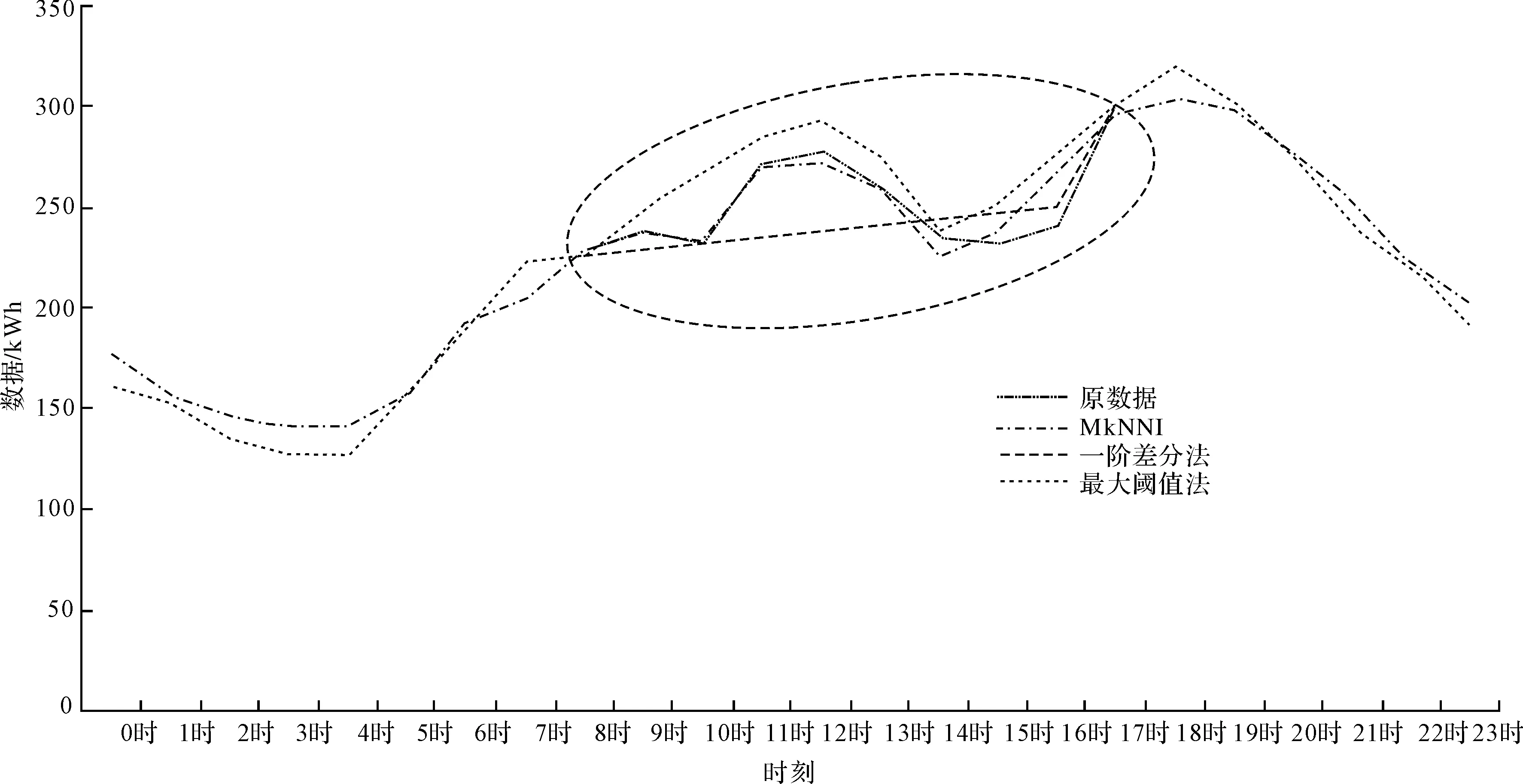
图4 连续时刻数据异常修正结果对比图
3 结 语
在数据统计方面,一阶差分法、最大阈值法和最近邻法,是比较常见的、易于实现的缺失值填充方法。公共建筑能耗监测数据具有比较明显的规律性、相似性和周期性,但天气、建筑类型等外界因素对不同类别的公共建筑能耗量有较大的影响,而最大阈值法进行数据修正时往往要参考至少近一个月的数据,由于时间范围过大,这就导致修正结果与实际监测值偏差较大,修正效果差。公共建筑能耗监测平台的监测数据是时间规范化后的差分数据,而非电表直接读取的累积值,所以当监测数据连续异常时,一阶差分法不能准确地预测能耗数据的变化趋势,在监测数据变化的拐点处,就会出现修正值与实际数据变化趋势完全相反的偏差,使得修正结果失真。相互最近邻算法(MkNNI)无论是单点数据异常还是连续时刻数据异常,都能够很好地逼近实际的能耗监测值,修正偏差在可接受范围内。
综上所述,比较之下相互最近邻法(MkNNI)对公共建筑能耗异常数据修正效果明显,对能耗各种异常情况的修正准确率较高,且算法简捷,满足对公共建筑能耗异常数据修正的要求,可以作为参考,用于公共建筑能耗数据异常的修正。但是,MkNNI算法对于连续24 h“0”数据或恒定不变数据的失真情况,修正效果不佳,有待进一步探索研究。
