双层样本中界面对太赫兹时域光谱的影响研究
2019-02-21詹洪磊陈儒王焱赵昆
詹洪磊 陈儒 王焱 赵昆


摘要:针对多层样本中界面对太赫兹时域光谱的影响问题,利用太赫兹时域光谱测试了由不同粒径制成的单、双层沙粒压片,获得了单、双层压片样本的太赫兹时域谱。结果表明,双层样本的单位厚度太赫兹峰值衰减系数明显小于单层样本的单位厚度衰减系数。因此,在研究双层样品太赫兹光谱响应时应添加某个系数以消除由样品的界面反射影响,且该系数与材料的特性有关。
关键词:太赫兹波;界面反射;吸收系数
中图分类号:TN761 文献标志码:A
引言
太赫兹(terahertz,THz)光谱是一种波长介于微波和红外之间的光谱,可用于检测材料和岩石的物理性质。在实际应用中,材料的腐蚀、老化、硬化、破壞、印刷、涂膜、粘结、复合等等都与材料的界面密切有关,因而在材料的太赫兹光谱表征方面,界面的反射特征对光谱检测结果具有重要的影响。表面光滑的样品的光谱反射率较高,表面粗糙的样品的光谱散射损耗较高,而双层样品中存多个界面,多界面间的反射特性对太赫兹光谱检测结果会造成更加复杂的影响。
目前,透射式太赫兹光谱是太赫兹检测的重要手段。物质对太赫兹波的吸收是材料太赫兹光谱信号衰减的主要原因之一,大多数材料具有较低的反射率。一般的样本(亦称为样品)是由颗粒经液压机压制而成,从而制得的压片具有光滑的界面,通过透射式太赫兹光谱可以检测样品的光谱特征。然而,颗粒内部的反射干扰(标准具)和界面间的反射特性仍可能影响样品材料的光谱特性,并且现有的测试方法基本是单个样品测试为主,多样品在测试过程中存在界面反射,使得多层样品的光学参数分析出现较大误差。因此,本文通过多样品太赫兹光谱研究了样品间的界面反射问题,阐述了样品界面太赫兹光谱反射的机制,包括样品界面间的多次反射信号、多样品所导致的吸收光谱数据与单一样品测试结果不一致等。对于多样品,常需要考虑或消除影响太赫兹检测中的界面反射问题,因而本研究可为复杂体系的太赫兹检测提供参考。
1太赫兹光谱检测原理
太赫兹波是频率在0.1~10 THz的电磁波,因此其在界面的反射特性符合电磁波的反射原理。对于正常入射的电磁波,照射厚度为d的薄层时,薄层的有效反射系数Reff和透射系数Teff可表示为:
式中:R01为从介质1反射到介质0的场反射系数;R10为从介质0反射到介质1的场反射系数;k1为波数。从薄样品中提取折射率通常需要使用数值方法求解式(1)或式(2)。如果样本足够厚,只能检测到第一个发射脉冲,R10变为零时,即可计算反射系数。在实验室环境中,通常使用单一样品进行太赫兹光谱检测,所获得的结果仅受样品的界面反射和内部吸收和散射的影响。
2实验方法
实验中选取沙粒粉末作为测试样品,通过筛网筛分出不同尺寸的沙粒,沙粒的平均直径分别为51um、61um、74um、84um、96um、106um,误差在+10um之内。为了获得更坚实的压片样品,压片时加入了对太赫兹波几乎透明的聚乙烯粉末(即直径约为50um的粘结剂)。将每个样品按照0.8 g沙粒和0.8 g聚乙烯粉末的比例进行混合,并将混合均匀的粉末置于20 MPa压力下进行3 min压片,最终得到直径为3 cm、厚度约为1.74mm±0.40mm的压片样品。
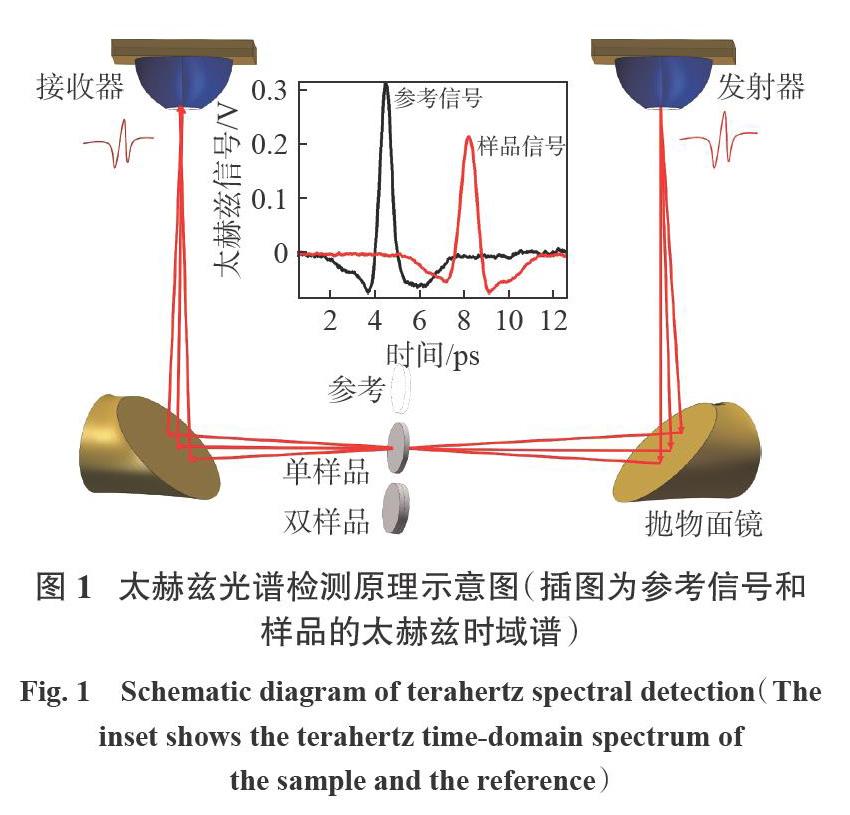
太赫兹光谱检测原理如图1所示。利用透射式太赫兹时域光谱仪对压片样品进行测试,测试时样品固定在相同位置,使得太赫兹波垂直穿过样品的中心。太赫兹源辐射的太赫兹波经抛物面镜反射照射到样品上,再经第二个反射镜反射被探测器接收。通过扫描发射器激励脉冲和探测脉冲之间的相对时间延迟可以获得太赫兹波的时间相关性,位于两个抛物面镜之间的样品也会引起时间延迟并使太赫兹信号减小。
为了避免水蒸气对实验的影响,在氮气环境下进行透射式太赫兹时域光谱测试实验。每次测试前先测试一次氮气作为参考信号,再对样品单独测试,结束后进行双样品(两个不同样本叠加在一起)测试。将沙粒尺寸相近的两个压片叠加在一起固定在相同位置进行测试,在两片叠加测试结束后,将两个样品互换位置继续测试,以保证测试的准确性。由此可以得到5组叠加样品测试数据,这些样品的颗粒直径组合分别是51um+61um、61um+74um、74um+84um、84um+96um、96um+106um。测试过程中,对每个测试样品进行3次测试,并取3次平均值来计算光学参数。将快速傅里叶变换应用于时域数据以获得频域谱,利用光谱的幅度和相位信息获得样品在太赫兹频段的吸收系数和折射率。
3结果与讨论
在氮气环境中扫描不同沙样压片,获得其太赫兹时域谱并对光谱进行处理分析,结果如图2所示。图2(a)为利用傅里叶变换获得的太赫兹频域谱,图中既包含6个单独测试样本的太赫兹时域谱,又包含了具有相近粒径叠加测试的双样品太赫兹时域谱。由图2(a)可看出,参考信号峰值在4.5 ps时为0.310 v,由于THz波通过样品折射引起的时间延迟,单个沙粒压片信号相对参考信号的时间延迟约为4.0 ps。随着沙粒直径从51um增加到106um,沙样压片的信号峰值从0.211 v降至0.125 v。单个沙粒压片中的信号衰减是由样品吸收、界面反射和内部散射引起的。可以看出,样本粒径越大,频域频谱中的截止频率越低。
双沙粒样品压片信号相对参考信号的时间延迟约为8.0 ps,是单个样品压片信号延迟的2倍,这是因为与单个样品压片测试相比,太赫兹波通过2层样本的光程是单个样品的2倍。对于信号幅值,51um+61um的信号峰值在12.1 ps时为0.170 v,峰值低于2次单次样品测试的信号,双沙粒样品压片的单峰随着沙粒直径的增加而减小,粒径从51um+61um增加到96um+106um,样本峰值从0.170v降至0.090v。
同时,在太赫兹时域光谱图中,时间较大时样本还存在明显的太赫兹时域波形,图2(b)显示了在26.5 ps到33.0 ps的延迟时间内的THz信号,这是由于THz波在压片样品界面间的内部反射,较小的信号表现为单个样本测试图像,如图2(c)的左侧所示。太赫兹波光程d与延迟时间△t之间的关系表示为
式中:n为样品的折射率;co为真空中的光速。如图2(c)的右侧所示,双样品测试可以获得较大延迟时间的太赫兹时域谱,样品中THz波的光程可以通过式(3)获得。由于具有2个相同光路的波的叠加,双样品的峰值大于单个样品的峰值。图2(d)为具有相近粒径和不相近粒径样品的双重样品测试结果,基于此可区分出不同尺寸的样品的延迟时间短且相近尺寸的样品的延迟时间长。这是因为不同尺寸的样品的折射率略低于相似尺寸的樣品。不同样品THz波的折射率可表示为
衰减系数β是由β=Ep-Ref/Ep-sam计算所得,Ep-Ref是参考信号峰值,Ep-sam是样品的信号峰值。d为压片样品的厚度,β/d对d的变化趋势如图3所示。其中,位于51um、61um、74um、84um、96um、106um处的数据点为单独样品测试的衰减系数,位于2个尺寸点中间的数据为附近2个叠加测试样品的衰减系数,为了除去样品厚度对实验结果造成的影响,衰减系数除以2倍的平均厚度得到单位衰减系数,如图3最下方圆形数据点所示。由图可知,当衰减系数除以2倍厚度时其衰减系数便小于单独测试的单位衰减系数。通过计算差值可知,当叠加测试样品的单位衰减系数除以1.5倍时,可使叠加样本的单位厚度衰减系数与单个样本趋于一致,此时存在10%的误差,即在10%的误差范围内可以认为叠加测试样品衰减系数符合单独测试样品的单位衰减系数。
根据样品的太赫兹时域谱,可计算得到样品的光学参数,如折射率、吸收系数、介电常数。不同测试样品的吸收系数如图4所示,频率范围为0.05~0.42 THz,其中实线为单个测试样品的吸收系数曲线,虚线为叠加测试样品的吸收系数。由图可知,随着频率的增大,不同测试样品的吸收系数均会增大,这主要是基线呈现上升趋势导致的。而颗粒尺寸越大的样品其增大的幅度也越大,曲线的基线有整体的提升。其中,当频率到达0.36 THz时,大颗粒尺寸的样品开始有明显的震荡,这是由于大尺寸的压片样品对太赫兹波存在米氏散射所造成。2片叠加测试样品的吸收系数均位于2片单独测试样品的吸收系数中间位置。为了更加清晰地显示,选取了3个频率对不同尺寸的测试样品的吸收系数进行分析,结果如图4左上角所示。由图可知,0.10 THz频率下所有尺寸样本的吸收系数较小,0.20 THz与0.30 THz频率下吸收系数均会随着尺寸的增加而增大,且0.30 THz的增加幅度更大。THz时域光谱入射光强度pE和出射光强度PR表示为:
式中:p1为THz波信号的衰减系数;pa为测试样品的吸收系数;pr为样品界面反射引起的反射损耗;ps为少量内部太赫兹波散射损失。
根据图4可以得出,无论对压片是单独测试还是叠加测试,吸收系数随着测试样品颗粒平均尺寸的增加而增加,衰减系数则不然,在叠加测试的过程中损耗会有所增加,这是由于叠加测试时太赫兹波会在样品内部反射及散射造成了比单个样品更加大的损耗。因此,为了在后续的实验中消除这种影响,在计算衰减系数的过程中,对于多层样本不能根据原始经验直接计算样品的单位衰减系数。为了消除样品内部反射和散射造成的损失,需要在除以厚度的基础上进一步除以一个相关系数,这个系数随样品本身材料的不同而变化。
4结论
通过单一压片测试及2片不同颗粒尺寸样品叠加测试,得到不同样本的太赫兹时域谱以及相关光学参数。研究表明:在太赫兹时域光谱中,表面光滑的样品存在一个延迟较大的太赫兹时域波形,样品叠加测试时这一现象会更加显著,不论样品是否进行叠加测试,随着样品沙粒尺寸的增大吸收系数也增大;对于界面的影响,仅考虑由界面因子计算的单位衰减系数的方法不适合于叠加测试,其原因是叠加测试时样品本身没有变化,吸收系数与颗粒尺寸呈现正相关关系,但在叠加测试的过程中,反射损耗和散射损耗更加强烈,因此,在计算衰减系数的过程中压片厚度的选择应考虑材料的具体特性。
