双排桩支护结构计算模型改进与分析

王 杰 韩 磊 徐云峰

（中国建筑第八工程局有限公司，上海 200122）

0 引言

双排桩是近年来发展的一种新型深基坑支护结构，由于其整体刚度大、不需要内支撑、方便施工等优点，已有较多成功的工程应用实例，同时双排桩的理论研究也引起了众多研究者的兴趣［1-8］。传统的设计计算方法将双排桩视为嵌入土中的门式框架，通过经验的方法人为给定作用在前、后排桩上的水土压力，进而采用结构力学的分析方法计算双排桩的内力和变形［9-10］。现行的建筑基坑设计规程［11-12］考虑双排桩和桩间土相互作用，将桩间土简化为一维的弹簧。考虑到该模型中桩端的边界条件设置难以反映桩土共同作用，郑 刚等［13］提出了改进的平面杆系有限元模型。也有研究者注意到了桩间土的土拱效应［14-15］和桩顶连系梁的变形协调作用［9，16］，此外研究者们还分析了带内支撑［17］以及锚索的双排桩［18-19］支护结构受力性能。Ohori等［20］将双排桩视为埋于土中的伯努利梁，假定桩间土为线弹性体，忽略桩顶连系梁的作用，建立了双排桩的控制方程，并采用解析和数值方法进行了求解。考虑到目前工程实际中桩顶除了设置连梁，还设置了配筋面板，作为材料堆放及车辆运输通道等，桩顶连梁对双排桩的约束较强。本文改进了Ohori等［20］的计算模型，将桩顶连梁设为刚体，采用数值方法将改进的模型与平面应变有限元模型计算结果进行了比较分析。研究表明，改进的Ohori模型能较好地反映双排桩支护结构的工作性状，计算简便，值得在实际工程中应用推广。

1 计算模型和控制方程

Ohori等［20］提出的分析模型为了计算简便，忽略双排桩之间联系梁板与桩顶冠梁的连接作用，将双排桩间土的受力和变形分析简化为平面应变问题，双排桩及桩间加固土体共同作用，组成基坑的支护体系。考虑到目前工程实际中桩顶除了设置连梁，还设置了配筋面板，有效提高了桩顶连梁的刚度，因此本文假定连梁为刚体，与前、后排桩之间为刚接，双排桩底与土体之间为铰接，如图1所示。双排桩的位移控制方程如下：

式中：yA为后排桩位移；yB为前排桩位移。

图1 改进的双排桩计算模型（模型1）

σA和σB满足如下方程：

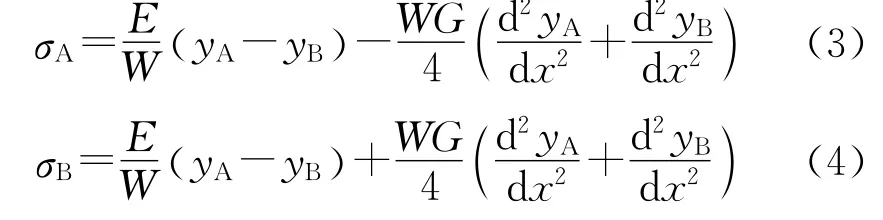
式中：E为桩间土弹性模量；G为桩间土剪切模量；W为前、后排桩间距。

考虑如下工况：基坑开挖深度为D，地层均匀。前、后排桩的距离为W，桩间土为线性弹性体。土压力为主动土压力，坑外水土压力根据实际地层确定采用水土分算或者合算，坑底土体与前排桩的作用采用文克尔地基模型。方程组（1）、（2）的边界条件为

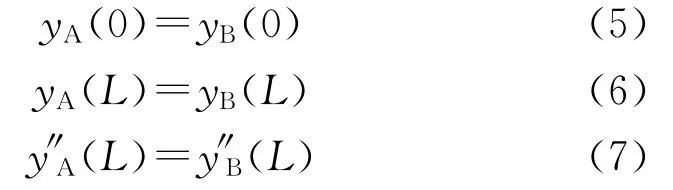
将边界条件和参数带入方程组（1）、（2），即可求出双排桩的位移函数，进而可以求出其弯矩，剪力等，也可以求出土体中的应力。

2 平面应变模型

双排桩平面应变模型如图2，将双排桩及桩间土体简化为连续体，桩端为铰支座。根据平面应变假设，取单位宽度的实体结构作为计算模型，通过刚度等效法，将前、后排桩简化为均匀的墙体，厚度计算公式为h=（式中d为桩距，Dp为前、后排桩直径）。

图2 双排桩平面计算模型（模型2）

根据分析模型假定条件，双排桩及桩间土的控制方程可写为：

式中：u为水平向位移；υ为竖向位移；εV为土骨架体积应变μ为剪切模量，μ=E/2（1+υ）；E为弹性模量；ν为泊松比；λ′、μ为Lame常数，λ′=Eν/（1+υ）（1—2υ）。

方程的边界条件如下：桩底及桩间土下边界为位移边界u=0和υ=0，后排桩背部为力边界条件σx=—pA，前排桩坑底上部为自由边界，坑底下部为力学边界条件σx=PB，桩顶及连系梁表面为自由边界。

3 改进的Ohori模型与平面应变模型对比分析

参考《基坑工程手册》［9］中的算例，取计算参数如下：基坑开挖深度10 m，围护桩长18 m，前、后排桩桩径1 m，桩距1.2 m，前、后排间距3 m，前、后排桩之间连系梁宽1 m，高0.3 m，前、后排桩与连系梁之间按固接考虑；坑外土层c=18 kPa，φ=22°，γ=18 kN/m3，地下水位深度3 m，本算例中坑外水土压力采用水土分算。混凝土弹性模量30 GPa，泊松比0.2，桩间土弹性模量E=5 MPa，泊松比0.25。为简便起见，本文仅分析了基坑土方开挖至坑底这一工况。

图3给出了改进的Ohori模型（模型1）和平面应变有限元模型（模型2）前、后排桩的水平位移和弯矩，图中z为桩体竖向深度变化范围，由图可知，后排桩的整体变形比前排桩大，这和文献记录的工程实测结果一致［13］。受桩顶连梁的作用，前、后排桩顶部的位移相等。桩顶以下，后排桩的位移大于前排桩的位移，因此桩间土处于受压状态。同时图3还显示模型1和模型2计算出的桩体位移和弯矩分布曲线相似，前排桩的位移和弯矩相差较小，采用模型2计算的后排桩位移和弯矩略小于模型1的计算结果。综上所述，改进的Ohori模型计算结果与平面应变有限元模型计算结果基本一致，说明改进的Ohori模型双排桩受力、变形合理，能较好地反映双排桩支护结构的工作性状，适合用于双排桩工程的设计和计算。

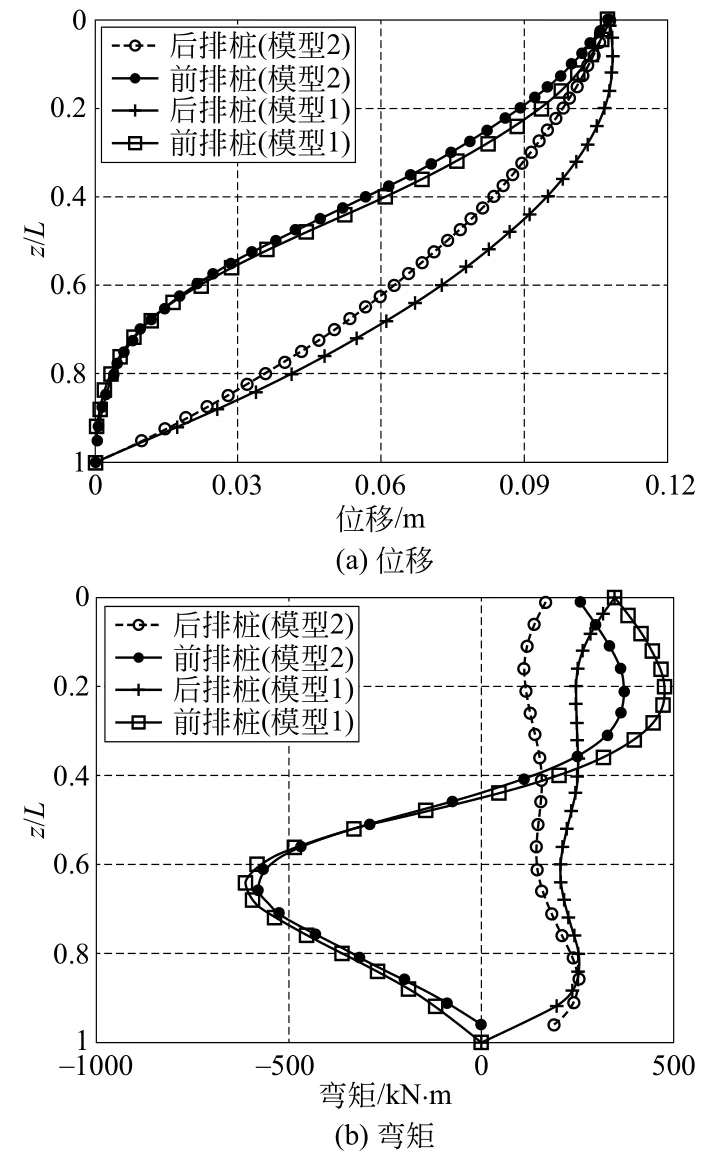
图3 前、后桩体计算结果比较

4 桩间土性质的影响分析

为了进一步比较桩间土的工程性质对两个模型计算结果的影响，本节通过参数分析，研究了桩间土弹性模量E变化时桩体水平位移的变化。为了简便起见，本节仅给出了前排桩的位移。桩间土的弹性模量E变化范围为0.5～32 MPa，算例其他计算参数同上节。

从图4可知，当桩间土弹性模量较小时，两个模型计算结果非常接近，当桩间土弹性模量变大时，两个模型的计算结果差别变大，但最大位移差约为最大位移的3%，因此，改进的Ohori模型的计算结果具有足够的精度。同时，还可以发现桩间土弹性模量的增大有助于减小双排桩的位移。

图4 前排桩位移随桩间土弹性模量变化

5 桩间土宽度对前、后排桩土压力的影响

通过以上分析可知，改进的Ohori计算模型具有足够的精度，能够满足工程计算的需要。现行的基坑支护设计规范中双排桩计算模型中将桩间土简化为弹簧模型，依此模型，桩间土对前、后排桩的压力相等。本文改进的Ohori计算模型将桩间土设定为线弹性模型，考虑了桩间土对前、后排桩的差异土压力。本节通过参数分析，研究了桩间土宽度变化对前、后排桩侧压力的影响。

双排桩间土宽度变化对前、后排桩侧压力的影响规律如图5所示，图中Dp为前、后排桩桩径，由图5可知，当桩间距从0.5Dp变化至8Dp时，桩间土对后排桩的土压力大于前排桩，土压力差随桩间距的增加而增加。从图中也可以看出，当桩间距小于4Dp时，作用在前、后排桩的土压力差小于5%，规范中将桩间土假定为弹簧模型是合理的，但是当桩间距大于4Dp时，作用在前、后排桩的土压力差距则比较明显，因此，不能再将桩间土假定为弹簧模型，采用本文提出的改进的Ohori模型更为合理。

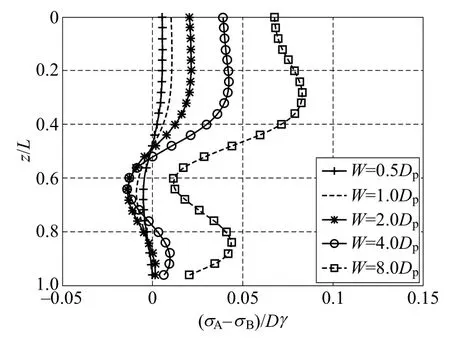
图5 桩间土对前、后排桩的压力随桩间距的变化

6 结论

本文通过数值计算和参数分析，比较了改进的Ohori双排桩计算模型和平面应变有限元模型的计算差别，并讨论了前、后排桩的桩间土弹性模量和双排桩间距变化时，前、后排桩的位移和土压力变化规律。得到结论如下：

1）改进的Ohori模型计算双排桩计算简便，精度可靠，可以用于双排桩的设计和计算。

2）桩间土弹性模量的增大有助于减小双排桩的位移，因此，在双排桩的设计和施工过程中，应该采取合理的措施加大桩间土弹性模量，以起到更好的支撑作用。

3）双排桩间距小于4Dp时，采用弹簧模型模拟桩间土的工作性状是合理的；双排桩间距大于4Dp时，作用在前、后排桩的土压力差距则比较明显，采用本文提出的改进的Ohori模型更为合理。

收稿日期：2018-09-19