区段强干扰下的列车运行调整研究
2019-02-21牛红霞张大勇
牛红霞,张大勇
(郑州铁路职业技术学院 运输管理学院,河南 郑州 451460)
0 引言
按图行车是铁路运输组织的基本要求,然而突发设备故障、恶劣天气等异常事件会影响运行秩序和运行安全[1],会使列车偏离既定的运行计划,引起运输秩序紊乱。高速铁路列车运行速度快、行车密度高,对运输秩序的波动较为敏感。当运输秩序受到干扰时,调度员需要及时调整,尽量恢复按图行车或减少列车运行秩序紊乱带来的影响[2]。弱干扰下的列车运行调整问题主要目标是在尽量短的时间内恢复按图行车、减少运输干扰波及范围;强干扰条件下的列车运行调整问题则需对列车运行计划进行重新制订并确定是否需要取消列车,主要目标是根据干扰情况确定受干扰区段的列车运行顺序、避免由于线路基础设施不满足列车运行而造成列车在途长时间停车[3]。
目前,国内外对弱干扰条件下的列车运行调整研究较多,而强干扰条件下的实时调度问题研究较少[4-5]。高速铁路在强干扰发生时的运行调整工作主要依靠调度员的经验判断人工指挥,不仅工作强度大而且方案有效性、科学性难以保证,因而以区段发生强干扰为背景,有针对性地对列车运行调整模型及相应求解方法进行研究。
1 问题描述
考虑在双线区段内的某区间单方向线路发生影响行车组织的强干扰情景,如线路中断、电气化铁路接触网中断等,列车无法按图运行,引起列车运行秩序紊乱。为明确问题,结合我国铁路实际进行以下假设:①区段为双线,正常运行时上下行线路分别使用;②区段某区间单条线路中断,另一条线路正常行车不受影响;③线路区段满足区间反向行车需求;④区段内各车站上下行到发线分别使用,忽略列车进路排布影响;⑤除强干扰情况发生区段外,其余区段满足列车正常运行条件;⑥在进入干扰区段前各列车按图运行。上述假设条件可简化问题建模并不影响问题的一般性。
区段强干扰示意图如图 1 所示,双线区段车站 2 和车站 3 间下行线路受强干扰影响中断,此时该区间组织双向行车。由于强干扰,需确定各列车通过该区段的顺序,列车不能运行在车站等待,故需根据干扰预测时长考虑沿线各站能力限制,决定各始发站尚未发出的列车是否取消。

图 1 区段强干扰示意图Fig.1 Example of section strong interference
2 模型构建与求解
根据现有研究[6-7],结合我国铁路实际情况,以事件-活动网络为基础,构建混合整数线性规划模型描述强干扰条件下的列车运行调整问题。
2.1 模型构建
2.1.1 事件-活动网络表述
以集合E表示事件,集合A表示活动,宏观层面线路网络可抽象为事件和活动构成的网络N=(E,A),事件-活动网络示意图如图2所示。根据事件类型不同,可将集合E分为到达事件集合Earr⊂E和出发事件集合Edep⊂E;根据活动类型不同,可将活动分为列车活动a∈Atrain(图2中实线)和间隔活动a∈Ahead(图 2 中虚线 )。
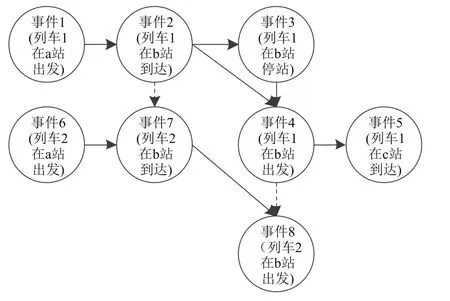
图2 事件-活动网络示意图Fig.2 Example of event-activity network
列车活动a∈Atrain可表示列车在区间内的运行a∈Arun或在车站的停站a∈Adwell;间隔活动a∈Ahead表示列车在车站的到发间隔或反向运行时在区间的运行间隔。基于事件-活动网络,可将列车在区段内的运行、停车等表示为各项事件的集合,显然列车运行图可以由全图所包含的所有事件表示,而各类行车间隔约束、车站能力约束等就可以由各类活动表示。于是,列车运行调整可以表示为实际所包含的各类事件,通过实际包含的各类事件与原列车运行图所包含各类事件的比较,实现对运行调整的量化并构建数学模型对其进行优化和求解。
2.1.2 相关符号定义
列车根据等级不同可以分为不同种类,当受强干扰影响时,列车运行时刻会偏离原有列车运行图,为明确描述各类约束条件,对相关符号定义如下。T为列车集合,分为下行列车集合T down⊂T和上行列车集合T up⊂T;S为区段内所有车站集合,s∈S;S m为区段内中间站集合,设区段内共有车站n个,1≤n≤m;Seg为相邻车站间的区间集合,seg∈Seg;qe为事件e的图定发生时刻;xe为事件e的实际发生时刻;Ωe为计划列车运行图,有为实际列车运行图为事件e的晚点时间为事件e的早点时间为事件e的晚点惩罚值为事件e的早点惩罚值;λt为列车t的取消罚数;te为事件e对应的列车;D为时间最大允许偏离值;M1为当日运行图周期,有M1= 1 440 ;M2为正整数参数,M2>M1。
2.1.3 目标函数
强干扰情况下的列车运行调整主要目的是使列车尽量按照原图行车、减少实际运行图与计划运行图偏离,同时为满足运输需求及机车、车辆、动车组等交路需要,尽量减少列车取消。由此确定目标函数为列车偏离计划运行时刻与取消造成罚数的加权最小值,计算公式为
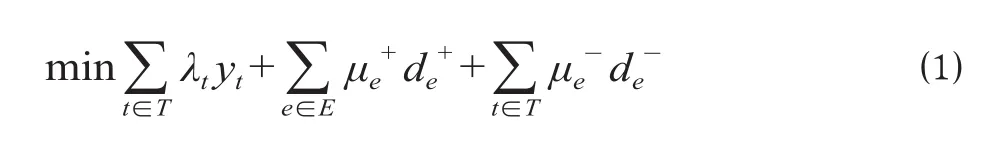
2.1.4 约束条件
干扰条件下的列车运行调整模型需满足一定的逻辑约束及列车在区段内运行的行车组织约束。我国列车运行图虽然基本为非周期列车运行图,但为缩减问题规模,可将列车运行图以天为单位进行单元化处理。在建模时考虑一天内的列车运行调整问题,对过表列车则顺延至下一个周期(后一天)处理。
(1)逻辑约束。表示各事件的基本时间关系,具体如下。

公式 ⑵ 表示取消列车转移至下一周期(后一天),从而避免对其他列车的干扰;公式 ⑶ 表示列车实际出发时刻不早于图定时刻;公式 ⑷、公式 ⑸ 分别表示事件的晚点、早点时间;公式 ⑹、公式 ⑺ 限制列车的最大晚点及早点允许值;公式 ⑻、公式 ⑼、公式 ⑽ 为相关变量的取值范围约束。
(2)行车组织约束。限制列车在区间的运行间隔时间及在站的出发、到达间隔时间,并保证同一时间同一闭塞区间内仅允许一列列车运行。当列车在区间内追踪运行时,区间运行间隔时间由区间追踪间隔时间决定;当列车在区间反向运行时,不允许对向列车由前方车站发出驶向该区间,此时运行间隔时间表现为先进入区间列车在该区间内的运行时间,需要根据具体列车运行状态确定区间运行间隔时间。相关约束的具体表现形式如下。

公式 ⑾ 表示占用同一运输资源的相邻事件e,f间隔时间应满足相应时间约束,根据列车运行状态不同,该约束可表示同向列车在站的到发间隔时间或者反向列车在同一站的到发间隔时间,La为相应的列车在区间内的最小运行间隔时间,同时由于M2>M1,因此可保证取消列车与其他列车间的区间运行间隔;公式 ⑿ 规定了同向列车在同一站出发或到达及反向列车在同一站的到达或发车需满足先后顺序;公式 ⒀ 中s及s'表示沿列车运行方向的两相邻车站,即s'为s的前方相邻站;公式 ⒁表示事件e,e'及事件f,f '分别属于同一列车,于是公式 ⒀ 至公式 ⒁ 就保证了通向列车在区间内不发生越行情况;公式 ⒂ 中a= (e,f)表示列车在区间的运行或在站停站活动,对应地,当其表示列车在区间运行时La表示列车在区间的最短运行时分,当其表示列车在车站停站时La表示列车在该站的最短停站时分。
(3)车站能力约束。发生强干扰条件下列车应在车站停车等待干扰结束,因此需要考虑车站能力的限制。在某列车到达某站时,该站的停留列车数可由在此时间之前到达该站的列车总数与从该站出发的列车总数之差表示,为确定某时刻某站的剩余能力,定义车站活动a= (e,f)∈Astation表示该站某出发列车与后续到达列车之间的活动,La表示同一到发线列车出发与后续列车接入同一股道间的最小接车间隔时间。设表示列车tf在车站s的到达事件,间隔活动子集为列车tf到达车站s与同向列车te到达车站s之间的间隔活动。同理,定义车站活动子集为列车tf在车站s站出发与同方向列车te在车站s到达之间的活动。相关约束的具体表现形式如下。
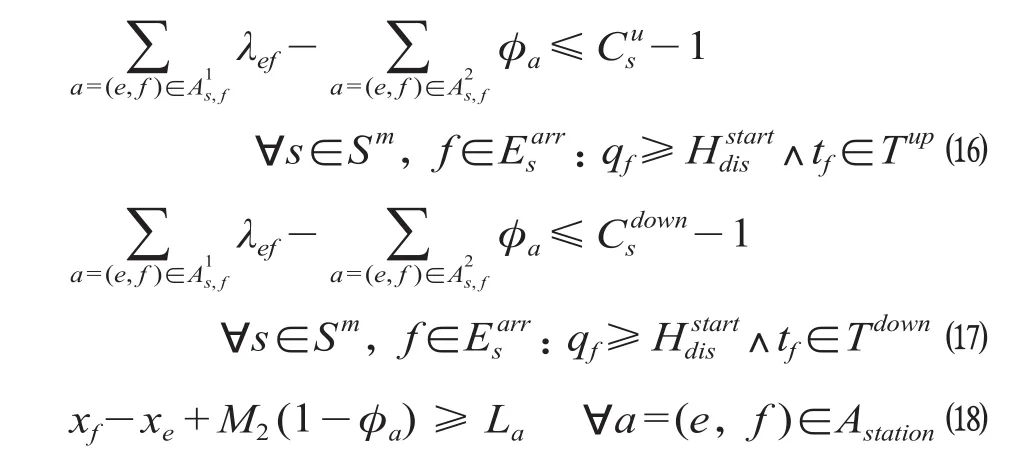
式中:φa为0-1变量,为当列车te在同向列车tf到达车站s之前从车站s出发时为1,否则为0;公式 ⒃ 和 公 式 ⒄ 中 的为车站s在列车tf到达之前已到达的同方向列车数量表示车站s在列车tf到达之前已发出的同方向列车数量分别为车站s的上下行到发线数量,于是公式 ⒃ 和公式 ⒄ 就保证在任意时刻任意车站至少有一条到发线可供列车tf使用为强干扰发生时刻;公式⒅保证同一到发线的已发出列车和后续到达列车间的最小间隔时间,La为对应间隔时间。
(4)在途列车不可取消约束。根据我国现有的调度规则,在强干扰发生时已经从始发站发出的列车应安排在中间站停车等待干扰结束后继续运行,而尚未从始发站发出的列车可根据实际情况和强干扰预测持续时间由调度部门决定是否发出或取消。为此需限制已发出列车的取消。相关约束可表示为
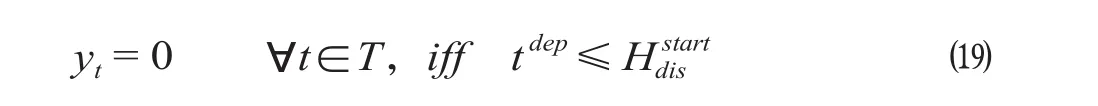
式中:t dep为列车t在始发站的发车时刻。
(5)列车取消均衡约束。当线路区段发生强干扰时,部分在强干扰发生时未从始发站发出的列车可能由于线路及沿途车站能力限制需要取消运行。由于发生强干扰的区段仅能维持单线运行,因此相较于取消双方向列车,显然取消单方向列车从线路通过能力角度更为有利。但是,由于考虑交路需要,取消单方向列车会严重影响运输秩序,甚至造成移动运营设备周转困难,从而进一步扩大运输秩序影响范围与时间。因此,从实际生产角度考虑,在考虑取消列车时应均衡考虑上下行方向列车。基于此,针对上下行不同方向同种类列车构成的集合p及p',提出列车取消的均衡约束。
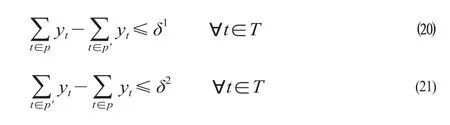
式中:公式⒇、公式(21)分别表示上下行同种类列车取消数量的差值限制,其中参数δ1,δ2分别为给定的上下行列车取消数量差值允许值,可根据实际情况设定。
(6)干扰前按图行车约束。根据假设条件,在强干扰发生之前列车应按照原有列车运行图运行,由此提出干扰发生前的按图行车约束为:
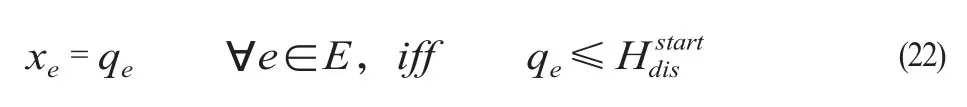
2.2 模型求解
目标函数 ⑴ 式及相应约束条件公式 ⑵ 至公式(22)构成一个混合整数线性规划模型。该类问题可由商业优化软件在较短时间内得到高质量的解。根据模型特点,采用CPLEX对所提出的模型进行求解,以便在较短的时间内得到较高质量的解。
3 实例分析
3.1 算例概况
以郑西高速铁路(郑州东—西安北)为例,验证模型的有效性。该线路全长538 km,区段内始发站为郑州、郑州东、洛阳龙门、西安北站(跨线列车视为接入站始发列车,以简化问题处理),考虑到郑州端有多个始发站且部分列车需经由既有线转入郑西高速铁路,算例以郑州西站为实际起点,共包括车站10个,区间9个,列车运行线125条,存在300 km/h (G类高速列车)和250 km/h(D类高速列车) 2种运行标尺,选取其中曹古寺—西安北的27对长途高速动车组列车运行线为例(G类高速列车26对,D类高速列车1对)进行验证。郑西高速铁路中间站到发线数量如表1所示,各区间列车运行时分如表2所示。

表1 郑西高速铁路中间站到发线数量 条Tab.1 Number of station lines of intermediate stations in Zhengzhou-Xi’an high-speed railway
3.2 计算实验
(1)强干扰场景设置。由于强干扰类型及发生地点具有一定随机性,因此假设强干扰表现形式为区间某方向线路中断,同时假设发生强干扰区间及持续时间如表3所示。
表3中场景1表示巩义南至洛阳龙门方向区间于10 ∶ 00起发生强干扰,持续时间分别为30 min、60 min,期间区间相反方向线路、信号设备运转正常,其他场景参照上述描述。
(2)计算结果。基于Visual Studio平台以C语言编程实现所述模型,调用ILOG CPLEX12.6以内置分支切割算法求解。相关参数设置为:对D类高速列车,取消惩罚值设为3 000,列车在站到达晚点罚数设为2,早点罚数设为1;对G类高速列车,取消惩罚者设为5 000,列车在站到达晚点罚数设为3,早点罚数设为2;事件最大允许偏离时间D设为30 min,考虑到实际调度指挥对时效性的要求,将求解时间上限设置为10 min,运行调整结果如表4所示。

表2 郑西高速铁路区间运行时分 minTab.2 Section operating time of Zhengzhou-Xi’an high-speed railway

表3 强干扰区间及持续时间Tab.3 Section strong interference location and duration
3.3 结果分析
根据计算结果可知,不同干扰场景对列车运行的影响不同,模型的求解时间及目标函数值亦不同,但各场景下模型均在短时间内得到了快速求解,可见模型能够满足现场调度生产对于时效性的需要。综合分析所得结果,得到以下结论。
(1)各场景中巩义南至洛阳龙门区间(上下行)接近正午时刻(11 ∶ 00)、干扰时间持续较长(90 min)情境下对列车运行的影响最为严重。
(2)相同区间内干扰持续时间越长,列车运行的影响越严重。
(3)算例所述干扰情境下均无列车取消,有利于移动运输设备的正常运用周转。
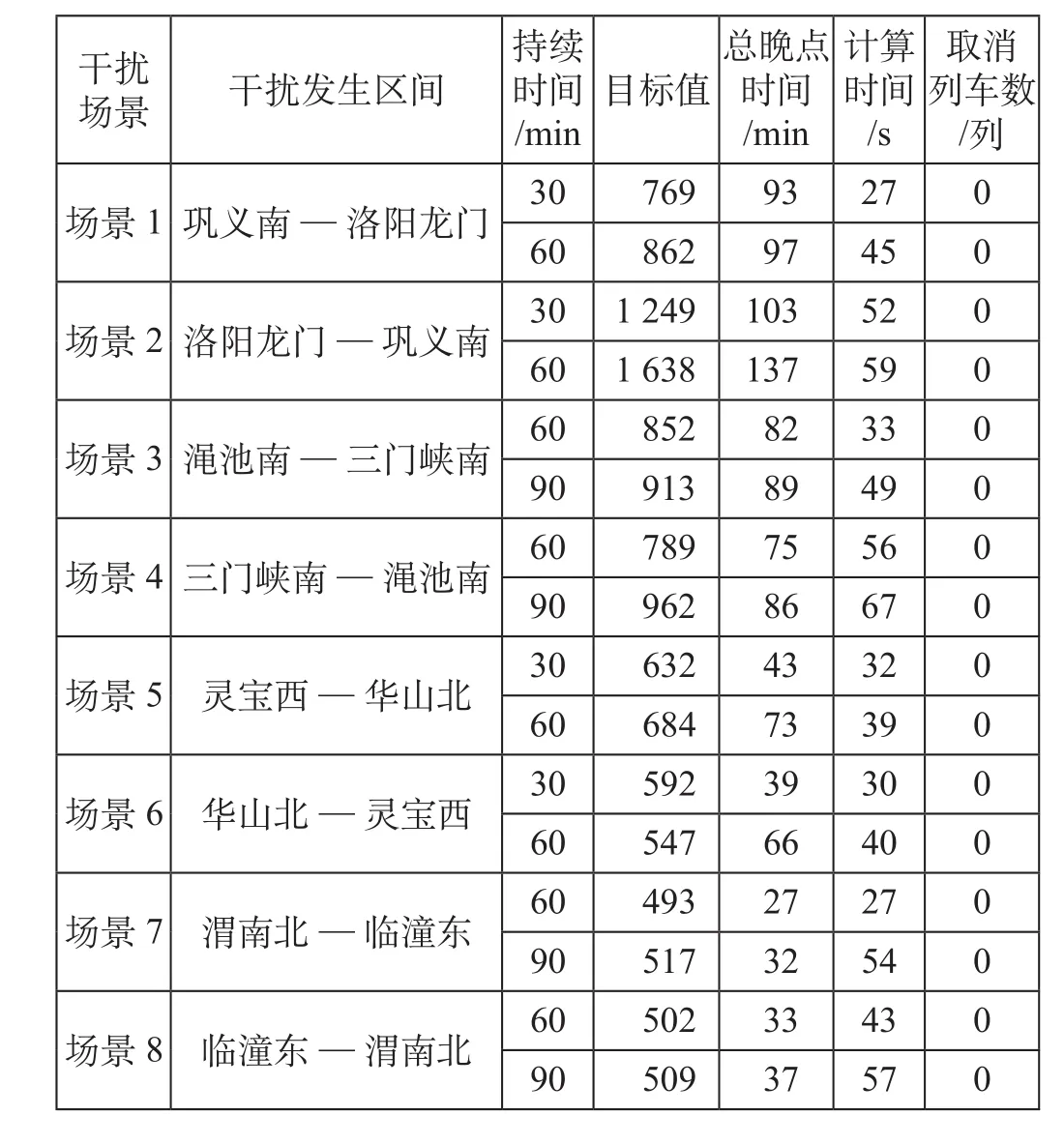
表4 列车运行调整结果Tab.4 Results of rescheduling
(4)所采用模型能够高效地求解强干扰条件下的列车运行调整问题,所得结果质量良好。
4 结束语
列车实时调度需要在短时间内综合各类影响列车运行的因素,快速求得可行方案指导列车运行进行相应调整。通过构建强干扰条件下的列车运行调整混合整数规划模型,采用CPLEX对模型进行求解,代替以往根据列车运行调度的经验指挥,是列车运行调度指挥智能化、自动化的重要方向,根据郑西高速铁路实际运行图数据进行的验证说明了模型的有效性。值得注意的是,研究假设上下行到发线分别独立使用,并且忽略了不同进路间的冲突,建模层面较为宏观,同时假设强干扰持续时间已知,在后续研究中,应进一步考虑车站进路排布约束,并考虑干扰持续时间不确定时的列车运行调整策略[8]。
