逆流自吸效应对页岩油储层坍塌压力的影响研究
2019-02-20邓富元何世明赵转玲
邓富元,何世明,赵转玲,汤 明,李 恒,刘 森
(1.油气藏地质及开发工程国家重点实验室(西南石油大学),四川成都610500;2.中石化中原石油工程有限公司钻井工程技术研究院,河南濮阳457001)
据统计,在钻进泥页岩地层时,发生的井眼失稳问题大部分是由地层中黏土水化膨胀引起的,影响泥页岩中黏土矿物水化的主要因素有井眼与地层之间压差、化学势以及毛细管力等[1]。就井眼和地层之间压差而言,国内外学者进行了大量研究,建立了各种多场耦合模型,分析了渗流引起的地层孔隙压力对井眼失稳的影响规律 。除此之外,Yu Mengjiao和 T.J.Ballard等人[7-8]通过试验,发现泥页岩中形成的化学势差会影响水和溶质离子的扩散程度;沈建文和马天寿等人[9-10]建立了溶质离子扩散模型,对井周孔隙压力的变化规律进行了分析。但由于页岩油通常赋存于低孔低渗致密泥页岩地层中,采用水基钻井液作为循环介质时,井眼中的水相和含油井壁接触时产生的毛细管力不容忽视[11-14]。因此,近年来国内外一些学者对此进行了研究,通过大量实验验证了欠平衡钻井过程中逆流自吸效应的存在[15-20];另外,M.Naseri和肖绒等人[21-22]基于油水两相流理论,分析了欠平衡钻井过程中的水侵规律,但是没有进一步分析水侵后的泥页岩井眼稳定情况。为此,笔者建立了考虑逆流自吸效应下的页岩油储层井眼失稳模型,分析了地层因素和钻井参数对井眼失稳的影响规律,以期为欠平衡钻井过程中的井眼稳定性预测和合理调整施工参数提供理论依据。
1 逆流自吸作用下的水侵模型
欠平衡钻井过程中,地层流体在一定欠压差条件下流入井筒。可是,当水基钻井液与井壁接触时,仍然存在指向地层的毛细管力,欠平衡压差可能无法全部克服毛细管力,因而导致井筒钻井液在毛细管力作用下自发进入地层,这就是逆流自吸效应[9]。页岩油储层的水侵是油水两相流动过程,欠平衡钻井过程中,水基钻井液侵入储层可简化为一维水驱油模型。该模型的假设条件为:页岩油储层为水湿地层且各向同性,为孔隙性介质;在水侵过程中,不考虑储层孔隙压力的改变,流体黏度和体积系数恒定;忽略流体重力的影响;油相与水相接触后不互溶。
基于上述假设条件,根据质量守恒和油水两相流达西定律,得到油水两相流连续性方程为[23]:

式中:r为到井眼轴线距离,m;K为页岩油储层的绝对渗透率,D;Kro和Krw分别为页岩中油相和水相的相对渗透率;μo和μw分别为页岩中油相和水相的塑性黏度,Pa·s;Bo和Bw分别为页岩中油相和水相的体积系数;po和pw分别为页岩中油相和水相的分压力,Pa;pc为油水毛细管力,Pa;Sw为含水饱和度;t为钻井液与井壁的接触时间,s;φ为页岩油储层孔隙度。
为了求解油水两相流连续性方程,可根据欠平衡钻井操作条件设定其边界条件。初始时刻边界条件:
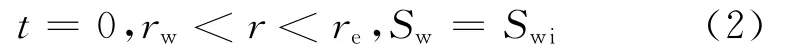
储层内边界条件:
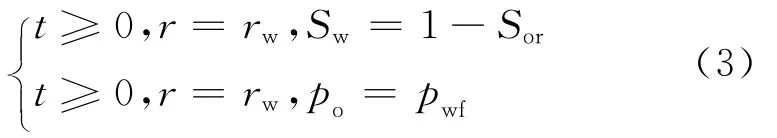
储层外边界条件:

式中:rw为井眼半径,m;re为储层外边界半径,m;pwf和pi分别为储层井筒流体压力和油藏边界压力,Pa;Sor和Swi分别为油藏束缚油饱和度和原始含水饱和度。
结合油水界面毛细管力方程[24]和两相相对渗透率方程[21],可以辅助分析求解得到毛细管力作用下油水两相流连续性方程数值解:

式中:θow为油水两相接触角,(°);σow为油水两相界面张力,N·m;A,B和c为常数,可以根据油藏特点由试验得出(本文取某油田经验值,A=0.9,B=0.8,c=4)。
欠平衡钻井地层参数:地层深度为3 100.00m,地层孔隙压力当量密度为1.20g/cm3,孔隙度为0.08,渗透率为0.8mD,初始含水饱和度为0.22,束缚油饱和度为0.25,储层油相黏度为25mPa·s,油相体积系数为1.2。
欠平衡钻井施工参数:水基钻井液密度为1.15g/cm3,钻井液滤液黏度为5mPa·s,钻井液滤液体积系数为1.0,井眼半径为241.3mm。
联立方程(1)、(5)和(6),运用 MATLAB编程可以求解得到井眼附近地层含水饱和度随欠压差值和钻井时间的变化规律,结果如图1和图2所示(无因次径向距离指r/rw,下同)。
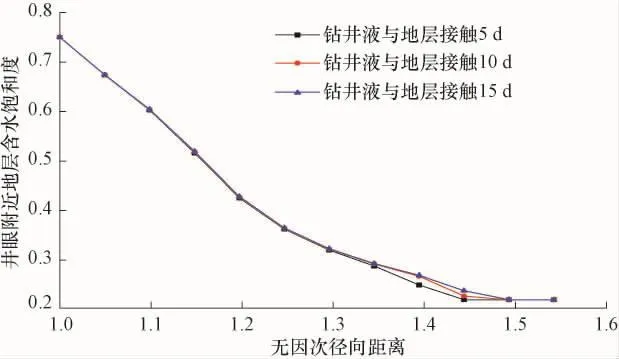
图1 毛管力作用下井眼附近含水饱和度随时间和无因次径向距离的变化规律Fig.1 Variation law of water saturation near borehole with time and dimensionless radial distance under capillary force
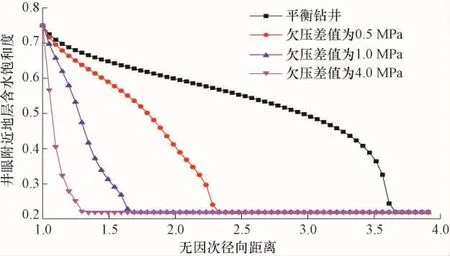
图2 不同欠压差值下钻井10d后井眼附近含水饱和度随无因次径向距离的变化规律Fig.2 Variation law of water saturation near borehole with dimensionless radial distance after 10days of drilling under different under-pressure
由图1可知,当水基钻井液与页岩地层接触时,在毛细管力作用下,水相不断驱动油相前进。当钻井液与地层接触5d后,约1.45倍井径附近含水饱和度已经达到地层原始含水饱和度。但是,随着钻井液与地层接触时间的增长,钻井液滤液侵入储层的深度会继续增加,而且由式(5)可知,毛细管力随含水饱和度增大而减小,因此15d时含水饱和度推进速率降低。
由图2可知,在欠平衡钻井过程中,不考虑滤饼对渗透性的影响,钻井10d后,钻井液侵入距离随欠压差值增大而增加。若地层孔隙压力等于井筒压力,钻井液只在毛细管力作用下进入地层,水侵深度约为井眼半径的3.7倍。分析认为,这是因为在欠平衡条件下地层与井筒之间存在指向井眼的压差,阻止流体进入地层,所以随着欠压差增加,钻井液侵入距离变短,侵入总量减少。所以,在欠平衡钻井过程中,为了降低钻井液侵入页岩油储层带来的影响,可以提高钻井速度,合理调整欠压差值。
2 水化作用对岩石力学特性参数的影响规律
对于水敏性页岩,由于地层中含有膨胀性黏土矿物,钻井液水分子进入黏土矿物晶层结构,会使层间距离扩大,发生晶格取代,造成黏土矿物体积膨胀。而地下岩石又处于约束状态,必然会在地层中产生膨胀应力,这种应力与地层原始应力叠加,就可能提高地层剪切破坏的趋势和可能性。国外学者[25]对不同的页岩样品进行了分析,发现岩石的强度特性与地层含水量有关。
国内学者针对泥页岩天然岩心也进行了吸水试验[26],发现弹性模量、泊松比及水化后的泥页岩黏聚力和内摩擦角均随页岩含水量出现规律性变化:

式中:E为岩石吸水后的弹性模量,MPa;E1和E2为系数,可由试验求得,根据经验值取E1=4×104,E2=11;W 和Wa分别为地层含水质量比和地层原始含水质量比;ν为地层岩石吸水后的泊松比;C(r,t)和C0为岩石吸水后与初始含水量下的黏聚力,MPa;φ(r,t)和φ0为岩石吸水后与初始含水量下内摩擦角,(°)。
根据岩石孔隙性结构,推导了岩石含水饱和度和地层含水质量比之间的关系:

式中:ρwf和ρs分别为钻井液滤液和页岩骨架的密度,g/cm3(取ρwf=1.20g/cm3,ρs=2.57g/cm3);Vw和Vs分别为岩石中含水体积与页岩骨架体积,cm3。
由式(7)—式(11)可分析得到页岩在欠压差为0.5MPa条件下发生逆流吸水后井眼附近岩石力学特性随含水饱和度的变化规律,结果如图3所示。

图3 欠压差为0.5MPa时页岩吸水后井眼附近岩石力学特性随无因次径向距离的变化规律Fig.3 Variation law of rock mechanical properties near borehole with dimensionless radial distance after shale water absorption under-pressure difference 0.5MPa
由图3可知,欠平衡钻井过程中,随着钻井时间的增长,由于近井附近钻井液滤液的侵入,含水饱和度增大,页岩油储层弹性模量、黏聚力和内摩擦角都降低,泊松比增大,从而降低了井眼稳定性。
3 逆流自吸作用下的井周应力模型
3.1 原地应力产生的井周应力
在页岩地层欠平衡钻进过程中,可以近似认为地层均质、各向同性,为线弹性材料,并且井壁围岩一直处于平面应变状态[1]。对于垂直地层,基于线弹性力学的基本理论,C.Fairhust推导得到了原地应力下的井周围岩有效应力分布公式[27]:
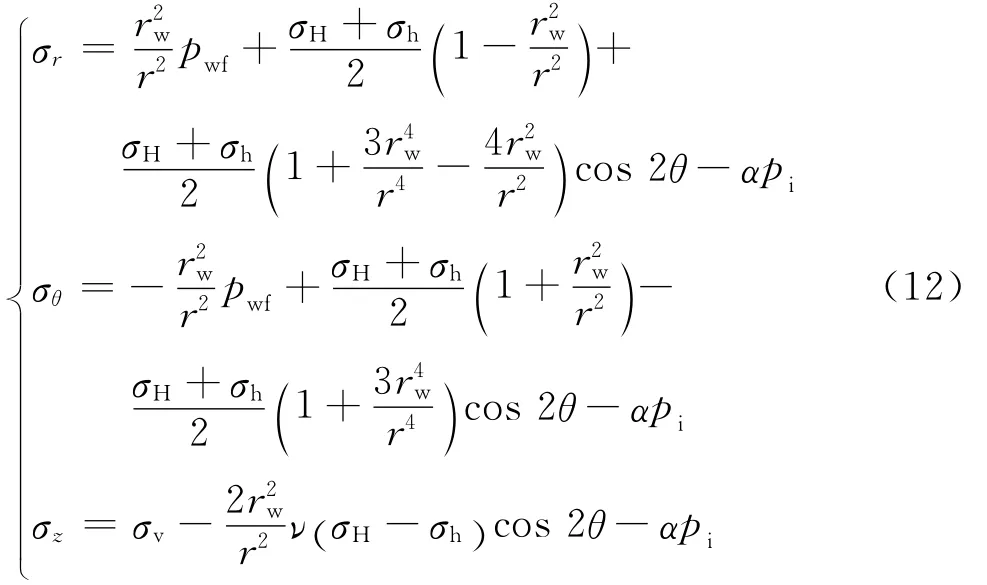
式中:σr,σθ,σz和σv分别为地层径向应力、周向应力、轴向应力和上覆地层应力,MPa;σH和σh分别为地层最大地应力和最小地应力,MPa;θ为井周角,(°);α为biot系数。
3.2 考虑水化应变作用下的井周应力
水化作用下的井周围岩应力应变(水化应变)平衡方程为[24]:

结合相应的边界条件σr|r=rw=pwf和σr|r→re=S(均匀的远场地应力),通过求解应力应变平衡方程,最终得到水化应变作用下的径向位移为:

式中:u为水化应变作用下的径向位移,m。
根据应变几何方程,可得到水化作用产生的径向和周向水化应变为:

垂向水化应变可利用泥页岩吸水试验得到的经验公式进行求取:

式中:k1和k2为膨胀系数,分别取值0.070 8和11.080 0;εrr,εθθ和εv分别为水化引起的径向、周向和垂向应变。
由式(13)—式(16)可得到考虑平面二维空间圆柱坐标系内因水化应变产生的水化应力:
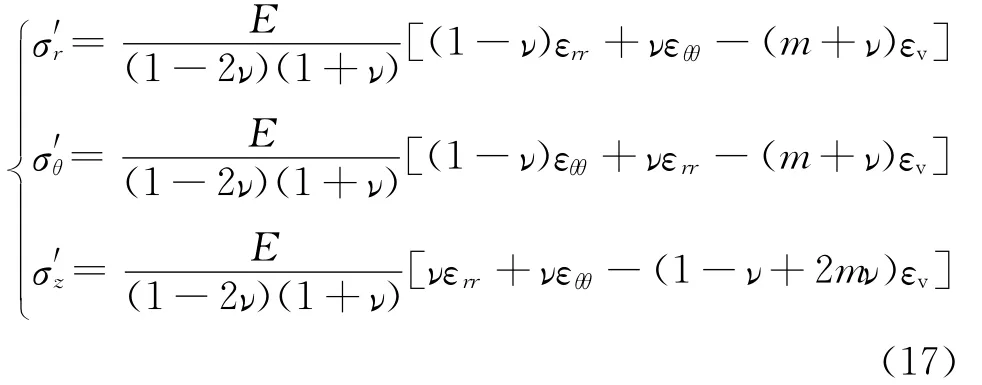
式中:σ′r,σ′θ和σ′z分别为水化后附加的地层径向应力、周向应力和轴向应力,MPa;m为各向异性比值,定义为地层膨胀后产生的水平面应变和垂直平面内的应变比值,一般由试验确定(本文取经验值0.71)。
3.3 逆流自吸对井眼附近地层孔隙压力的影响
在多相流渗流介质中,常采用有效平均孔隙压力pi表示孔隙压力。当储层中流体介质为油水两相时,有效平均孔隙压力可表示为:

3.4 页岩吸水后井周有效应力分布
井眼有效总应力由2部分组成:一部分是泥页岩水化应变产生的水化应力,另一部分是由原地应力产生的应力。由此可得到页岩油储层吸水后的井周应力为:
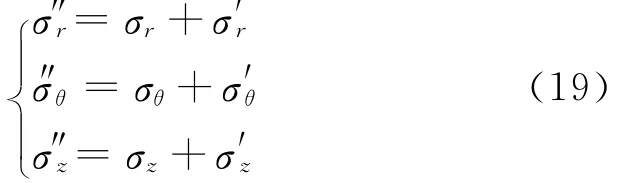
式中:σ″r、σ″θ和σ″z分别为页岩油储层吸水后的地层径向应力,周向应力和轴向应力,MPa。
对直井,根据岩石主应力分析,可以发现岩石的最大和最小主应力分别是周向应力σ″θ和径向应力σ″r。
4 页岩油储层坍塌应力影响因素分析
基于逆流自吸作用下的钻井液水侵模型,分析了页岩油储层应用水基钻井液钻进时井眼附近的含水量变化规律,根据储层岩石力学参数随含水量变化规律,就可以通过井周应力模型分析钻井参数(欠压差值)、地层因素(孔隙度和渗透率)和钻井液性能(表面张力)等对页岩油储层坍塌压力的影响规律。
4.1 页岩油储层井眼坍塌压力分布规律
为了研究欠平衡钻井过程中力化耦合条件下孔隙性页岩油储层井眼附近地层的坍塌压力变化规律,采用了以下基础地质力学数据:最大主应力当量密度为3.2g/cm3,最小主应力当量密度为2.1g/cm3,垂向主应力当量密度为2.5g/cm3,初始黏聚力为6.69MPa,初始内摩擦角为36.76°,其他数据同前文。图4所示为页岩油储层井眼稳定模型求解思路,图5所示为欠压差值为0.5MPa(钻井液密度为1.183 5g/cm3)时,钻井10d后井眼周围地层坍塌压力当量密度随无因次井径和井周角的变化规律。
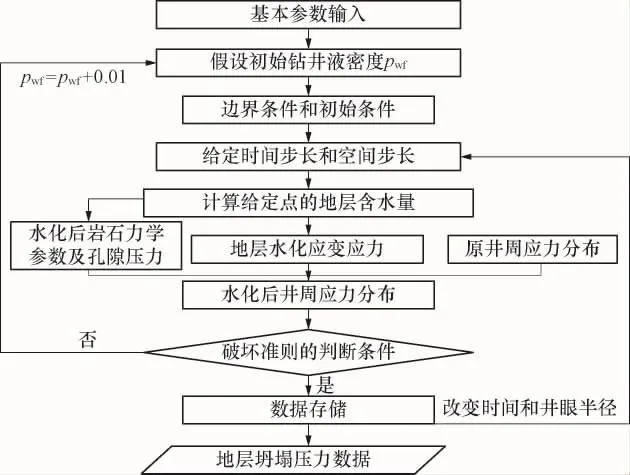
图4 页岩油储层井眼稳定模型求解流程Fig.4 Solution flow of borehole stability model

图5 井眼周围地层坍塌压力随无因次径向距离和井周角的变化规律Fig.5 Variation law of formation collapse pressure equivalent drilling fluid density around borehole with dimensionless well radius and well round angle
由图5可知,随着无因次径向距离增大,坍塌压力当量密度逐渐降低,无因次径向距离为1.30处的坍塌压力当量密度约为1.125g/cm3,低于钻井液密度,所以能维持该位置处的地层稳定;同时,随着井周角的变化,井眼周围地层坍塌压力当量密度呈现出规律性变化,井周角为90°和270°时的坍塌压力当量密度最大,地层越容易发生坍塌失稳;井周角为180°和360°时的坍塌压力当量密度最小,地层最稳定。
4.2 欠压差值对坍塌压力的影响
钻井10d后不同欠压差下井眼附近地层坍塌压力当量密度随径向距离的变化规律见图6。

图6 钻井10d后不同欠压差下井眼附近地层坍塌压力随无因次径向距离的变化规律Fig.6 Variation law of formation collapse density with radial distance near borehole under different under-pressure difference after 10days of drilling
由图6可知,随着欠压差值增大,钻井时间相同情况下水侵距离越近,同一地层处的地层坍塌压力当量密度越小。分析认为,这是因为水化应力与地层含水饱和度有关,随着欠压差值增大,钻井液进入地层的阻力增大,侵入量减少,含水饱和度降低,所以水化效果越弱,同一半径处的坍塌压力当量密度越小。
不同欠压差下的最大井径扩大率如图7所示。

图7 不同欠压差下的最大井径扩大率Fig.7 The maximum hole diameter enlargement rate under different under-pressure difference
由图7可知,欠平衡钻井过程中,欠压差值为2MPa时井眼最大扩径率最小,表明在该地质条件下欠压差值为2MPa时最合理。分析认为,当欠压差值小于2MPa时,钻井液密度相对较大,但钻井液在毛细管力作用下侵入页岩地层,页岩水化起主导作用,产生的的水化应力较大,降低了井眼稳定性;相反,当欠压差值大于2MPa时,页岩水化能力较弱,钻井液密度也很小,不足以有效支撑井壁,所以钻井液对井眼的支撑作用开始占主导地位,井眼稳定性也随之降低。
4.3 地层渗透率对坍塌压力的影响
以欠压差值2MPa钻井10d后,渗透率对井眼附近地层坍塌压力和最大井径扩大率的影响情况分别如图8和图9所示。
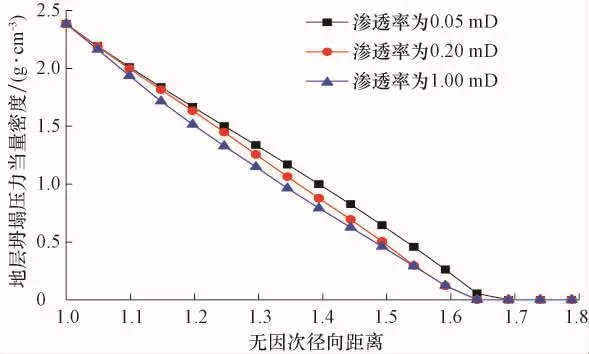
图8 欠压差2MPa条件下钻井10d后渗透率对井眼附近地层坍塌压力的影响Fig.8 Influence of permeability on formation collapse density near borehole after 10days of drilling at under-pressure difference of 2MPa

图9 欠压差2MPa条件下钻井10d后渗透率对最大井径扩大率的影响Fig.9 Influence of permeability on maximum hole diameter enlargement rate after 10days of drilling at under-pressure difference of 2MPa
由图8可知,随着地层渗透率增大,同一地层处的地层坍塌压力当量密度减小。由于毛细管力与地层绝对渗透有关,由式(5)可知,当页岩地层绝对渗透率增大时毛细管力减小,侵入地层的钻井液滤液减少,页岩水化能力减弱,井眼附近地层同一位置处的坍塌压力当量密度减小。
由图9可知,随着渗透率增大,井眼最大井径扩大率减小。由于渗透率增大,毛细管力作用减弱,钻井液滤液侵入地层的距离减小,同一地层处的含水饱和度就会降低,所以当欠压差值恒定(钻井液密度不变)时,井眼最大扩径率会减小。
4.4 孔隙度对坍塌压力的影响
在欠压差值为2MPa条件下钻井10d后,孔隙度对井壁附近地层坍塌压力的影响情况如图10所示。

图10 欠压差为2MPa下钻井10d后孔隙度对坍塌压力的影响Fig.10 Influence of porosity on collapse pressure after 10days of drilling at under-pressure difference of 2MPa
由图10可知,随着地层孔隙度增大,地层坍塌压力当量密度增大。分析认为,地层孔隙度的增大引起了地层总毛细管力的增大,从而提高了井眼附近的含水量,加剧了页岩地层水化,最终使井周地层坍塌压力增大。
不同孔隙度下的最大井径扩大率如图11所示。

图11 不同孔隙度下的最大井径扩大率Fig.11 The maximum hole diameter enlargement rate at different porosity
由图11可知,最大井径扩大率随着页岩地层孔隙度增大而增大,并且页岩地层的孔隙度与最大井径扩大率基本呈线性关系,拟合相关系数达到99.929%。
4.5 界面张力对坍塌压力的影响
不同钻井液的表面自由能是不一样的,因此当钻井液与页岩地层接触时,产生的界面张力会有区别。研究了欠压差为2MPa条件下钻井10d后不同界面张力下钻井液侵入地层后坍塌压力的影响规律,结果如图12、图13所示。

图12 欠压差2MPa条件下钻井10d后界面张力对坍塌压力的影响Fig.12 Influence of surface tension on collapse pressure after 10days of drilling at under-pressure difference of 2MPa

图13 不同界面张力下的最大井径扩大率Fig.13 The maximum hole diameter enlargement rate under different surface tension
由图12、图13可知,随着界面张力的不断增大,地层坍塌压力当量密度增大,最大井径扩大率也增大。分析认为,这是因为界面张力增大加强了地层毛细管力作用,使侵入地层的钻井液含量增大,加剧了页岩水化,从而增大了井眼附近地层坍塌压力当量密度;同时,最大井径扩大率也随界面张力的增大而增大。
5 结 论
1)页岩油储层在采用水基钻井液欠平衡钻进时,由于逆流自吸效应的存在,井筒钻井液滤液仍然会进入地层,使得井眼附近地层含水饱和度升高。
2)井眼附近地层含水饱和度的升高会影响地层岩石力学特性,即岩石泊松比增大,岩石弹性模量、黏聚力和内摩擦角减小。
3)欠平衡钻井过程中存在逆流自吸效应时,随着欠压差值增大,地层坍塌压力减小,最大井径扩大率先减小后增大;随着渗透率增大,地层坍塌压力减小,最大井径扩大率减小;随着孔隙度增大,地层坍塌压力增大,最大井径扩大率增大;随着界面张力增大,地层坍塌压力增大,最大井径扩大率增大。
