困油压力对滑动轴承润滑状态的影响*

(1.宿迁学院机电工程学院 江苏宿迁 223800;2.成都大学机械工程学院 四川成都 610106)

外啮合齿轮泵(简称为齿轮泵)是一种泵送油液的动力元件，应用极其广泛。但该泵的结构会引起困油现象[1]，造成困油压力急剧升高，使轴和轴承受到很大的冲击载荷[2-3]，并引起振动和摩擦副润滑失效等严重危害[4-6]。虽然卸荷槽可以部分地缓解困油的压力峰值[7-8]，但要彻底消除困油现象也不可能[1]。

目前，在泵轴几何设计和轴承-轴颈润滑设计方面[9-10]，所依据的外载荷(即泵从动轮上径向力)计算，多是基于过渡区液压力线性分布假设的静态计算方法[9-10]。而动态困油压力和动态液压力分布对轴承-轴颈间润滑状态的影响，目前除定性描述外，尚无相关定量分析的文献报道。为此，本文作者在前期动态困油压力和动态液压力分布的研究基础上，建立困油压力与轴承外载荷的时变关系，以期获得困油压力对泵用滑动轴承的润滑状态的定量影响，为轴承的全流体润滑设计提供依据。

1 滑动轴承润滑状态

摩擦学中常用油膜比厚λ描述两摩擦面之间的润滑状态。当λ<1时，处于边界润滑状态；1<λ≤3，处于混合润滑状态；λ>3，处于流体润滑状态[11]。针对泵用滑动轴承，λ是轴承-轴颈间的最小油膜厚度与其综合粗糙度之比，设计上应尽量满足如式(1)所示的纯流体润滑状态要求。

λ=hmin/σ>3⟹hmin>3σ

(1)

式中：hmin为轴承-轴颈间的最小油膜厚度，mm；σ为其综合表面粗糙度，mm。

2 最小油膜厚度计算

在给定边界的情况下，对应于泵从动轮上的总径向力，为保证轴承-轴颈间纯流体润滑状态的设计要求，单个有限宽的从动轮轴所必需的承载量系数[11]为

Cr(Fr)=FrΔ2/(2ηωφd4)

(2)

式中：Cr为所必需的承载量系数；η为润滑油平均动力黏度，Pa·s；Fr为从动轴上的总径向力，N；ω为轴颈角速度，rad/s；φ为轴的宽径比；d为轴直径，mm；Δ为轴承-轴颈的直径间隙，mm。

轴颈-轴承所能提供的承载量系数，取决于轴承的包角(入油口和出油口所包轴颈的夹角)、相对偏心率和轴的宽径比φ[11]。当轴承的包角(120°，180°或360°)和φ给定时，经过反求换算，相对偏心率则可由式(3)求出。

Cp(γ)=Cr(Fr)⟹γ(Fr)

(3)

式中：Cp为能提供的承载量系数；γ为轴颈-轴承的相对偏心率，其定义为轴颈-轴承的偏心距与半径间隙之比。因此，轴颈-轴承间的最小油膜厚度为

hmin(Fr)=0.5Δ[1-γ(Fr)]

(4)

3 承载量系数的多项式拟合

若轴颈-轴承是在非承载区内进行无压力供油，且设流体动压力是在轴颈与轴承衬的180°的弧内产生，则不同γ下所能提供的承载量系数值[11]，如表1所示。

表1 不同相对偏心率下承载量系数值(φ=0.8)Table 1 The bearing capacity factor at different relative eccentricity with the width diameter ratio of 0.8

采用Excel软件的“插入→图表→XY散点图→趋势线→多项式→选项→显示公式”的功能，可以得出对应的拟合多项式。由于多项式的最高阶次只能为6，故以表1中的γ=0.7作为分界点，进行如式(5)所示的两段拟合。需要注意的是，拟合时γ的第一个数值须转换成Excel所要求的默认值1，且“显示公式”中系数的小数点位数要足够，这里取8位，否则拟合值跟实际值差距很大。

(4)

式(4)中第1、2段拟合多项式的系数，如表2所示。表1中数据的多项式拟合曲线，如图1所示，与表1中的数据非常吻合。

表2 承载量系数的多项式拟合系数(φ=0.8)Table 2 Polynomial fitting coefficients of bearing capacity factor with the width diameter ratio of 0.8

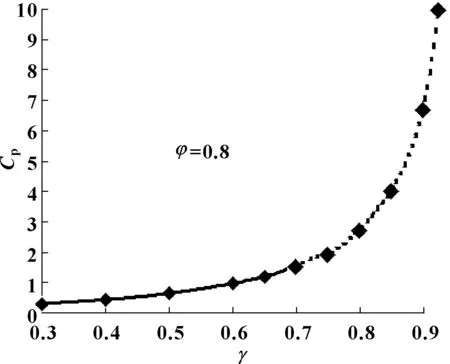
图1 φ=0.8时承载量系数随相对偏心率变化曲线Fig 1 Variation of bearing capacity factor with relative eccentricity at the width diameter ratio of 0.8

4 无困油压力时轴承润滑状态分析

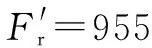
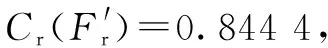
5 有困油压力时轴承润滑状态分析

因泵侧隙一般很小，所以泵齿轮传动的几何计算，仍按无侧隙的方式处理。为保证泵均匀而连续地供油，重合度应大于1。为此，文献[1,12-13]以啮合点处主动轮上的啮合半径s作为困油过程的位置变量，如图2(a)所示，建立出偏向主、从动轮o1、o2的两困油区内困油压力p1、p2的计算式。其中，位置变量s的计算周期[1,12-13]为

s∈[rbtanαa-pb,rbtanαa]

(6)

式中：rb为基圆半径，mm；pb为基节，mm；αa为齿顶圆压力角，rad，均为齿形参数的函数。

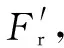
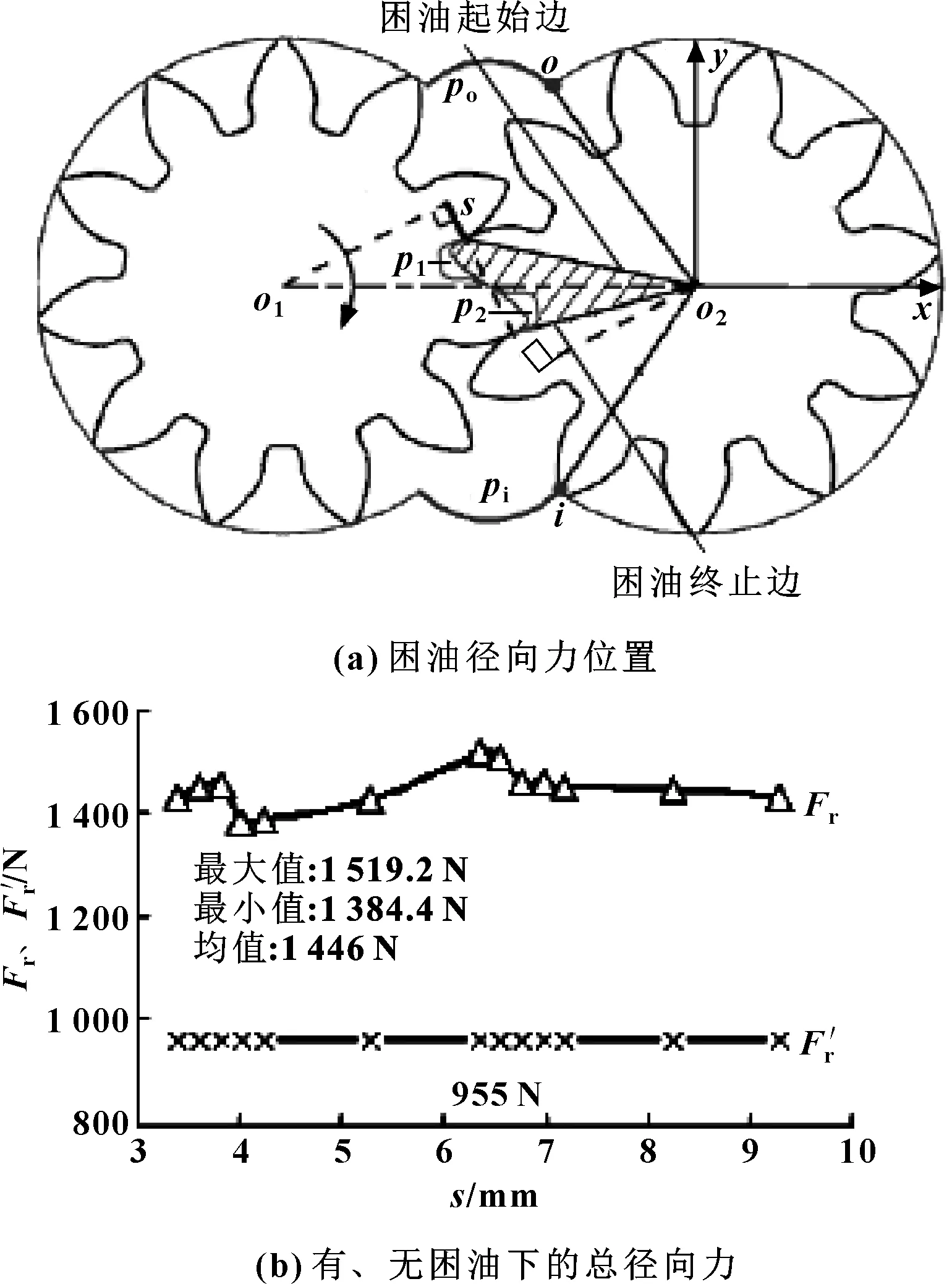
图2 困油径向力位置及有、无困油下的总径向力Fig 2 Position of trapped-oil radial force(a) and total radial forces with and without trapped-oil(b)

表3 困油压力的影响数据Table 3 Relative bearing data affected by trapped-oil radial force

6 结论

(1)困油压力导致径向力增大，最小油膜厚度降低。某案例计算结果表明：困油压力导致径向力增大45%～59%，最小油膜厚度降低19.6%～24.3%；困油压力造成了滑动轴承-轴颈间处于混合润滑状态，达不到流体润滑状态的原始设计要求。

(2)困油压力影响较大，应在结构创新上尽量缓解困油现象，并在泵轴设计中应充分考虑困油压力的影响。