牙轮钻头单金属密封结构优化研究

(西南石油大学机电工程学院 四川成都 611500)

牙轮钻头单金属密封结构于1991年由中国石油大学罗纬和国洪领[1]提出，因其具有耐高温、耐磨损的特点而被广泛应用。1998年美国贝克休斯公司研发出SEMS结构[2]，2003年该公司在SEM的基础上，开发出新一代的SEMS2结构[3]，如图1所示。

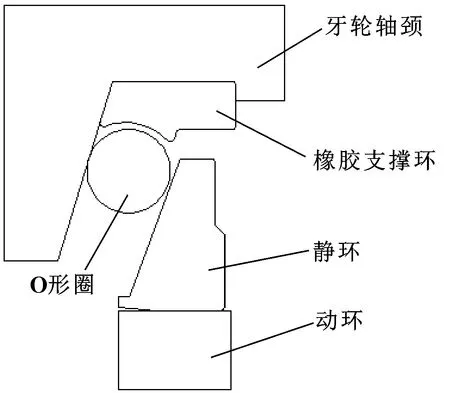
图1 单金属密封结构示意图Fig 1 Sketch map of single metal seal structure

国内外学者对单金属密封结构进行了许多研究，张宝生和陈家庆[4]介绍了单金属浮动密封的应用特点、润滑模型、计算机辅助工程(CAE)在理论研究中的应用、表面强化技术在单金属浮动密封中的应用等；孙健等人[5]模拟装配SEMS结构并分析了其在不同环境下的应力变化特征；张晓东等[6]分析了SEMS2结构在不同环境下密封面的应力特征；BURR[7]提出了弹簧补偿功能的密封结构；KOLTERMANN[8]开发出磁力密封结构。

单金属密封结构动密封面的接触应力不仅影响静环和动环接触面的磨损情况，同样也影响密封面间润滑油膜的形成。接触应力过大会造成动密封面磨损加速，接触应力较小会使润滑脂泄漏并使钻井液侵入轴承腔。密封结构参数变化会对动密封面接触应力的大小产生影响[9]，而国内外文献缺少单金属密封结构参数变化对动密封面接触应力的影响规律的研究。因此，针对单金属密封结构结构，本文作者研究不同的静环斜面倾角、静环楔入角和动密封面长度对动密封面接触应力的影响。

1 单金属密封结构参数

单金属密封结构的动密封面是由静环和动环组成，其中动环的结构参数由钻头的大小决定，因此研究单金属密封结构参数变化对接触应力的影响，即为研究静环的结构参数的影响。静环的结构示意图如图2所示，其中，α为静环斜面倾角，β为静环楔入角，L为动密封面长度。而针对φ215.9 mm的牙轮钻头、内径为50 mm的单金属密封结构，静环斜面的倾角取值范围为α=13°～21°[10]；静环楔入角取值范围为β=1°～9°[10]；动密封面的长度取值范围是2.5 mm≤L≤4.5 mm[12]。

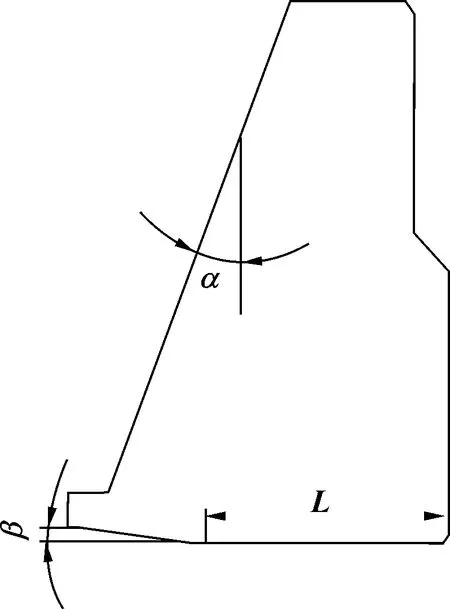
图2 金属静环示意图Fig 2 Sketch map of metal static ring

2 有限元模型的建立

单金属密封结构为轴对称结构，因此用CAD建立二维模型，并导入ABAQUS建立有限元分析模型，如图3所示。

图3 有限元分析模型Fig 3 Finite element analysis model

在选择材料时，橡胶支撑环及O形密封圈均采用丁腈橡胶，选取Mooney-Rivilin函数模型描述橡胶材料在变形时的特性。金属材料选择9CrW18Mn，其弹性模量为203 GPa，泊松比0.3[13]。边界条件设置为对牙轮轴颈的Y方向约束，载荷步主要分为5步，如表1所示。

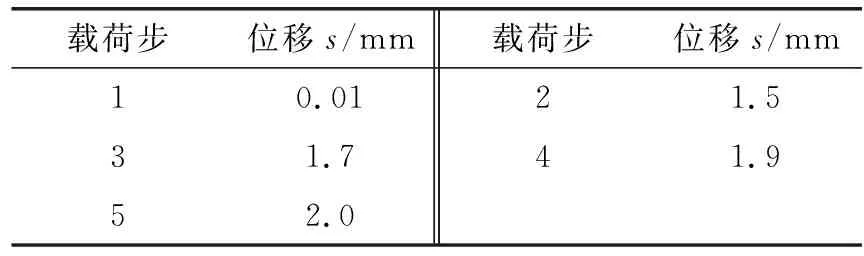
表1 有限元分析载荷步Table 1 Finite element analysis load step

其中，第一步是使结构之间建立接触，位移较小；第二步为使金属静环与橡胶支撑环接触；接下来的载荷步开始压缩橡胶支撑环，最终装配完成后轴向位移是2.0 mm。为了便于比较，后面的分析均采用同样的模型、材料、分析步和轴向位移。

3 结构参数对接触应力的影响分析

3.1 原始结构接触应力分析

研究的原始结构单金属密封结构如表1所示。有限元分析得到的其动密封面的接触应力云图如图4所示。可知：接触应力最大值在动密封面的外侧，其值为26.88 MPa，平均接触应力为8.08 MPa。

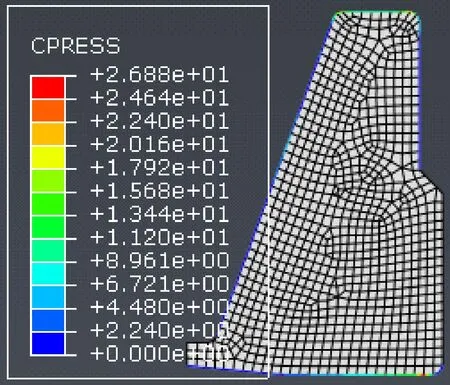
图4 动密封面接触应力云图Fig 4 Contact stress image of dynamic sealing surface

3.2 结构参数变化对接触应力的影响

为了研究静环斜面倾角α、静环楔入角β和动密封面长度L变化对动密封面接触应力的影响，将参数分为5个水平进行有限元分析，即：α为13°、15°、17°、19°、21°；β为1°、3°、5°、7°、9°；L为2.5、3.0、3.5、4.0、4.5 mm。

3.2.1 静环倾角的影响

在保持静环楔入角β以及接触长度L不变的情况下，改变金属静环倾角α的大小，得到动密封面沿接触路径的接触应力分布曲线，如图5所示。

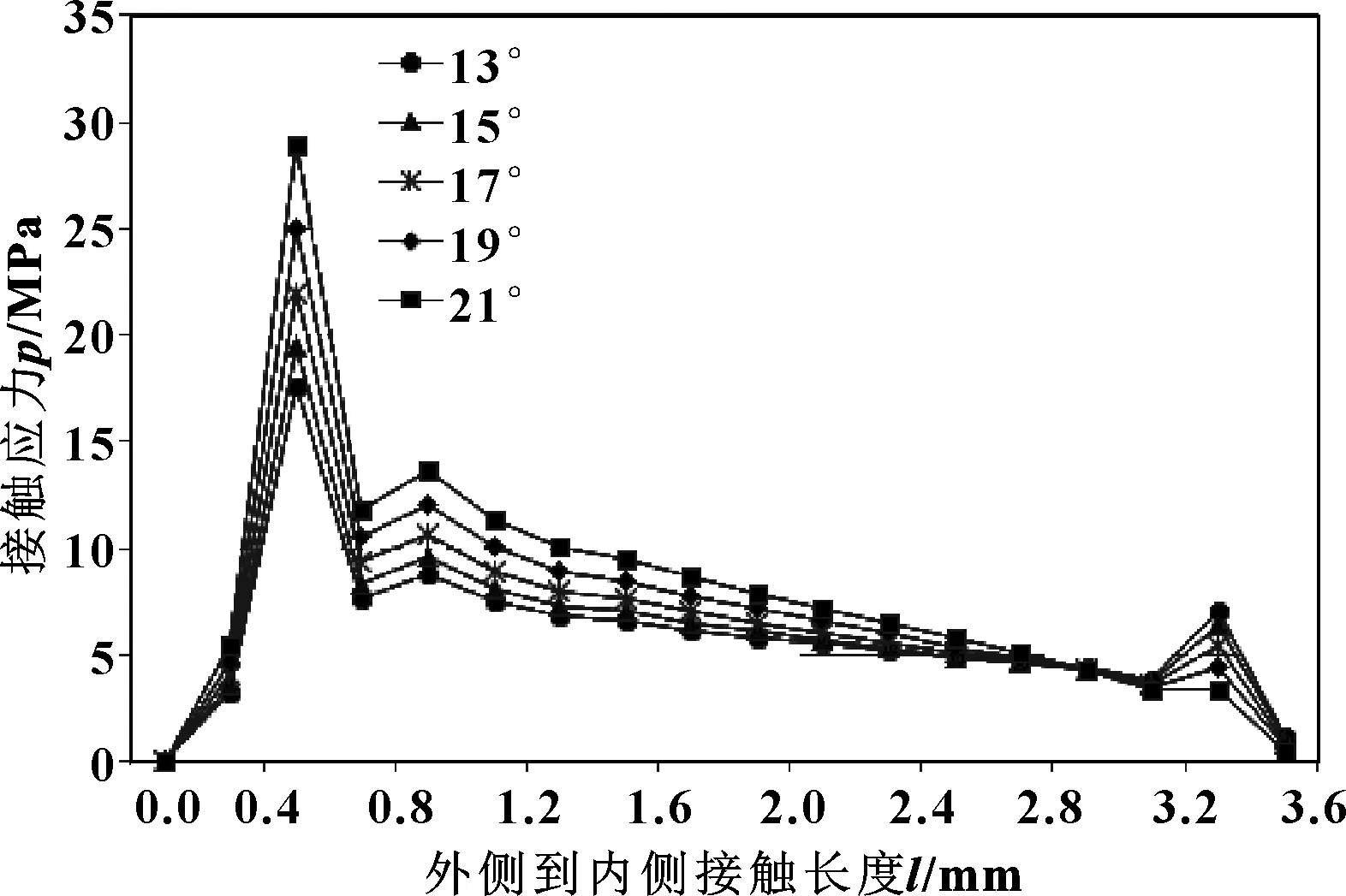
图5 不同金属静环倾角对动密封面接触应力的影响Fig 5 Influence of different tilted angle of the roller shaft neck on contact stress of dynamic sealing surface

由金属静环倾角变化的曲线可知：5种静环倾角下都呈现出动密封面外侧接触应力较大、内侧接触应力较小、中间接触应力变化较为平稳的趋势，并且都在距离外侧0.5 mm处达到最大值。在静环倾角从13°到21°的变化过程中，最大接触应力逐渐增加，并且在0.5～3.3 mm的接触长度上波动程度增加。

3.2.2 接触长度的影响

在设定金属静环倾角α、静环楔入角β不变的情况下，改变动密封面接触长度进行了分析。图6所示为不同动密封面接触长度下接触应力变化曲线。

当接触线长度为2.5 mm时两端接触应力较高，中间较低；其余4种动密封面长度均是动密封面外侧接触应力达到较高，内侧较低并且中间分布较为均匀，在长度为3.0～4.5 mm时最大接触应力呈上升趋势，但变化不明显。

3.2.3 静环楔入角的影响

在设定金属静环倾角α以及接触长度L不变的情况下，改变静环楔入角β进行了分析。计算发现静环楔入角β的变化对动密封面接触应力的影响并不大，其中，楔入角为1°和9°时金属静环的接触应力云图如图7所示，其接触应力变化仅变化0.27 MPa，接触应力的最大值仍然在动密封面的外侧。

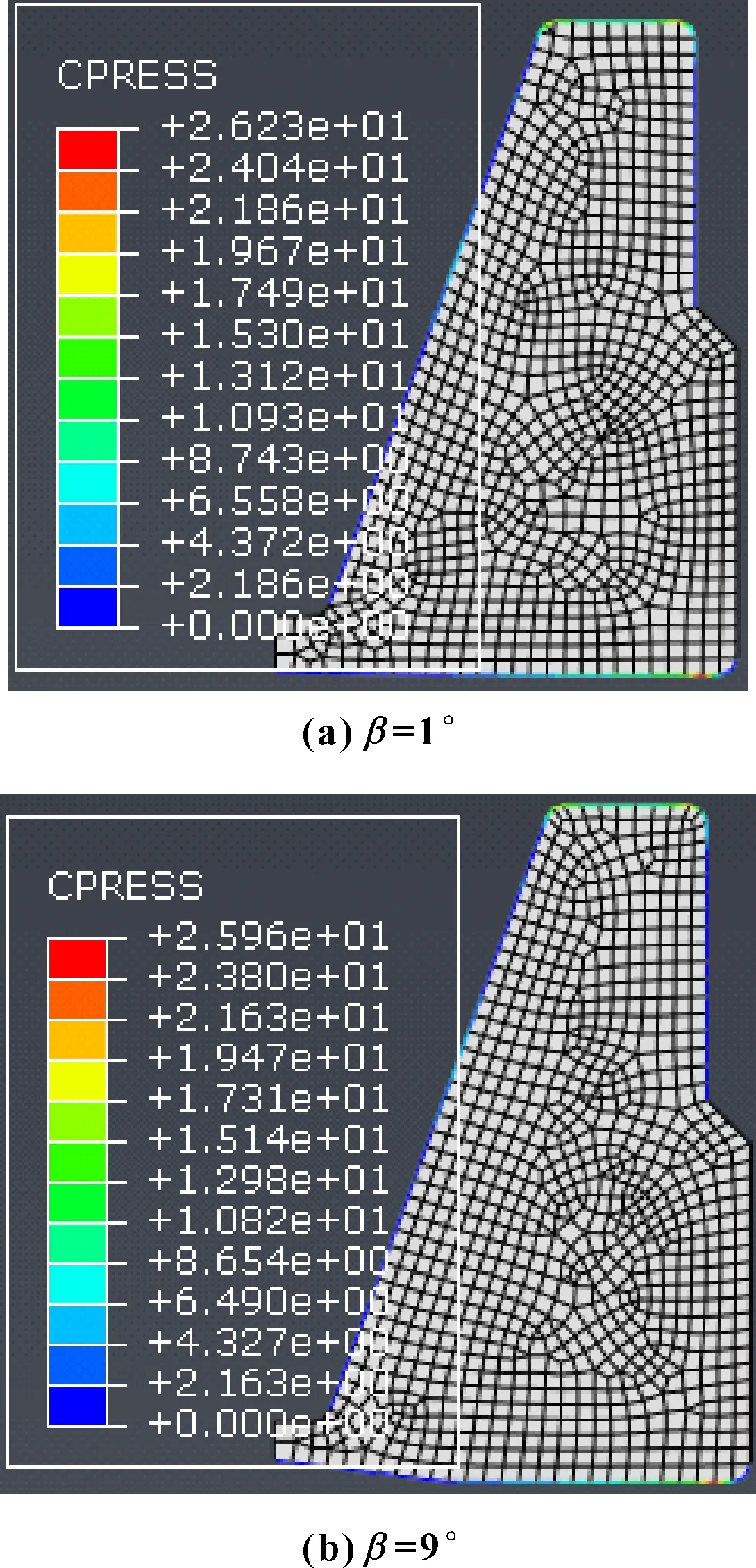
图7 楔入角为1°和9°时金属静环的接触应力云图Fig 7 Metal static ring contract stress images when the wedge angle is 1°and 9°

4 单金属密封结构参数优化

上述研究表明，单金属密封结构尺寸参数的变化是影响动密封面接触应力的关键，合理的尺寸优化能够增大接触应力，提升密封的可靠性。为研究单金属密封结构的最优参数组合，采用DOE实验，分析不同参数对动密封面接触应力影响的主次水平。

4.1 正交试验设计及结果

表2所示为正交试验的因素和水平表，即3因素5水平的正交试验。

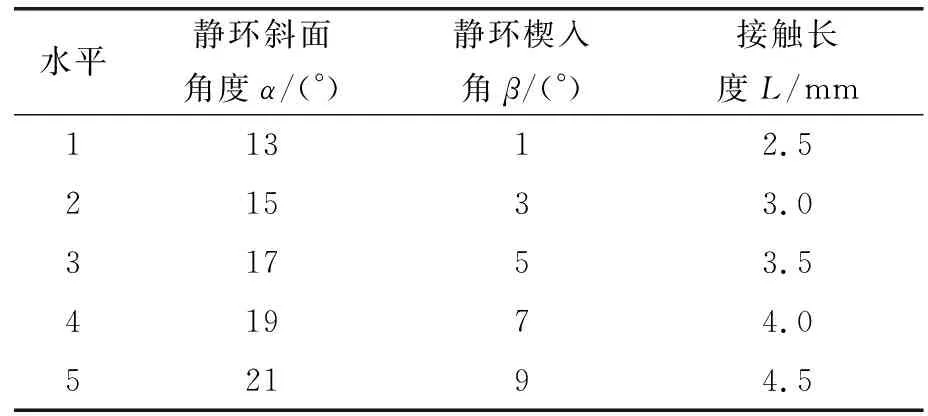
表2 因素和水平表Table 2 Factor and level

正交试验需要25次试验，利用ABAQUS分析得到不同结构参数下动密封面的最大接触压力，如表3所示。

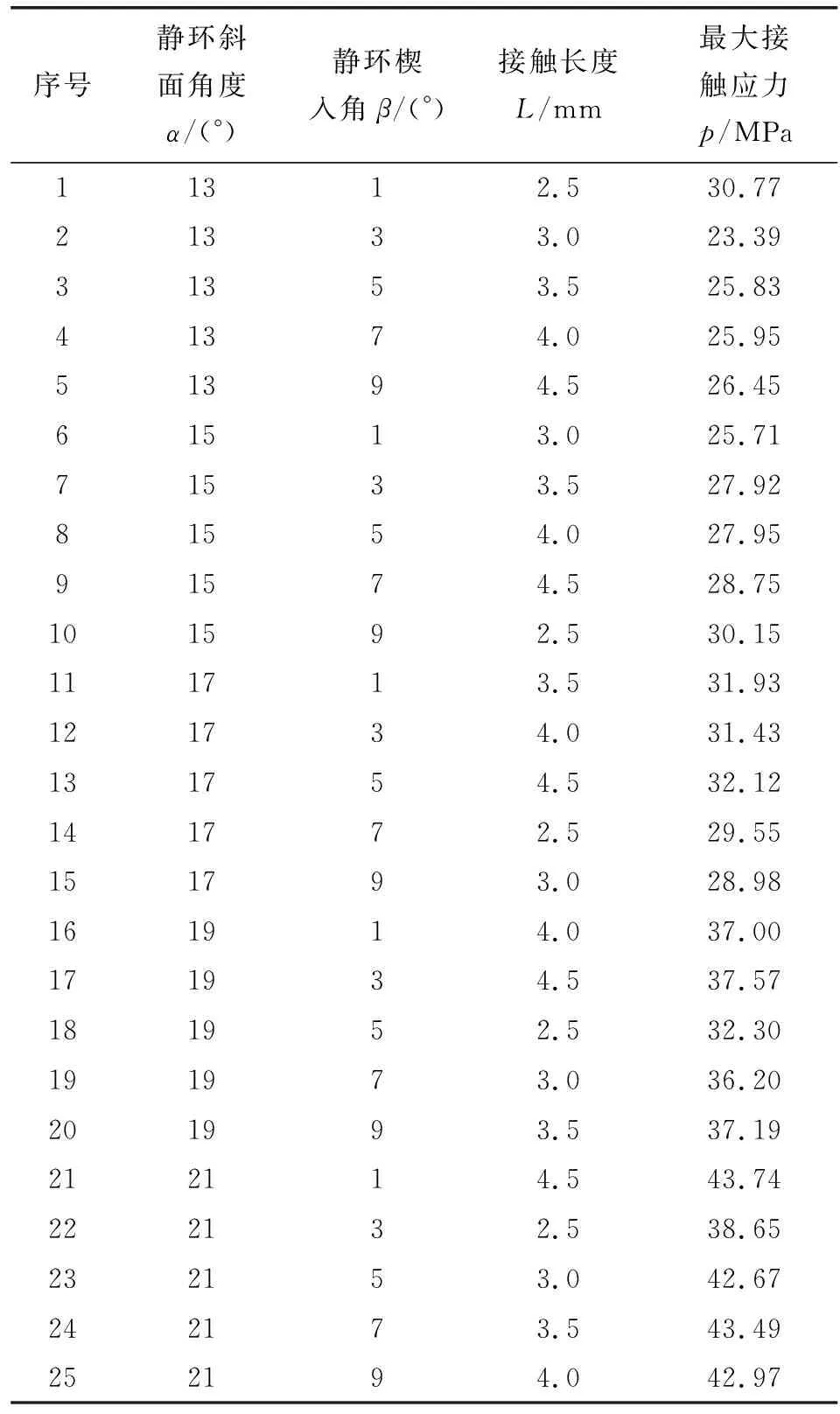
表3 正交试验结果Table 3 Orthogonal test results

4.2 结构参数显著性分析

利用极差分析法，研究不同密封结构参数对动密封面接触应力的影响。根据正交试验结果，得到了各水平接触应力的最大值、极差、3个因素的主次顺序以及最佳参数组合，如表4所示。

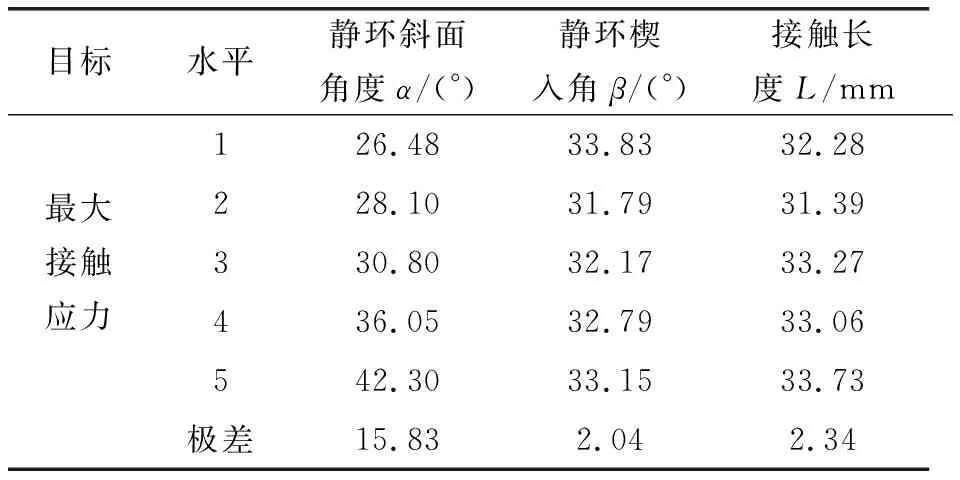
表4 极差分析表Table 4 Range analysis

由极差分析结果可知：影响动密封面间接触应力的结构参数主次顺序依次为静环斜面角度α、接触长度L、静环楔入角β。即静环斜面倾角对接触应力影响较大，而静环楔入角和接触长度相对较小。该结果验证了前面的规律性分析结果。

分析得到的最佳参数组合为α=21°，β=1°，L=4.5 mm，即为正交分析表中第21组试验。与优化前比较，优化后的最大接触应力由26.88 MPa上升至43.74 MPa，增幅为62.72%；平均接触应力由8.05 MPa上升至9.42 MPa，增幅为17.02%。

5 结论

(1)静环斜面倾角从13°到21°的变化过程中，最大接触应力逐渐增加，且都出现在动密封面的外侧0.5 mm处，动密封面中间的接触应力分布较为均匀；动密封面接触长度从2.5 mm到4.5 mm的变化过程中，接触应力逐渐增大，但是增幅并不明显；静环楔入角从1°增至9°时，接触应力呈减小趋势，但变化幅度并不大，其最大值仍然分布在动密封面的外侧。研究表明：静环斜面倾角对接触应力影响较大，而静环楔入角和接触长度相对较小。

(2)通过正交优化分析，得到了影响动密封面间接触应力的结构参数主次顺序依次为静环斜面角度α、接触长度L、静环楔入角β，且最佳参数组合为α=21°，β=1°，L=4.5 mm。

(3)与原始结构比较，优化后最大接触应力为43.74 MPa，增加62.72%，平均接触应力为9.42 MPa，增加17.02%。