优化搜索策略的KCF目标跟踪算法

杨志方，陈 曦

武汉工程大学电气信息学院，湖北 武汉 430205

目标跟踪是计算机视觉领域中的研究热点，在民用和军事领域都有着非常广泛的应用。民用方面包括视频监控、人机交互、虚拟现实、移动机器人等；而军事方面则包括无人机、战场监控、精确制导以及空中预警等。运动目标跟踪，即通过目标的有效表达，给定第一帧图像中目标初始状态（通常为位置或范围），在图像序列中寻找与目标模板最相似的候选目标区位置的过程［1］。尽管多年来目标跟踪领域已取得了不错的进展，但它仍是一个富有挑战性的问题。跟踪技术的研究重点依旧在于：如何解决部分遮挡、平面外旋转、背景相似以及尺度改变等［2］。如何建立有效的外观模型是跟踪算法能否成功的关键。

最早将相关滤波用于目标跟踪的是误差最小平方和滤波器［3］（minimum output sum of squared error filter，MOSSF），它采用灰度特征，并用峰值旁瓣比来判断目标是否被遮挡或跟踪失败。核循环结 构 检 测 跟 踪［4］（circulant structure of tracking-by-detection with kernels，CSK），速度大幅领先其之前的滑窗检测法。而文献［5］引入了循环矩阵和核的概念，并在核相关滤波器中提取方向梯度直方图特征，利用循环矩阵在傅里叶空间可对角化的性质大大降低了运算量。高效卷积算子的跟踪［6］（efficient convolution operators for tracking，ECO），从模型大小、样本集大小和更新策略3个方面加速，在多个顶尖目标跟踪数据集上性能都是第一，而且没有过拟合的问题。文献［7］在判别相关滤波器的框架下引入一种空间正则化组件，根据空间位置惩罚相关滤波器系数，扩大了训练图像区域并提高了分类器性能。文献［8］计算采样后分块粒子的权值函数，再利用霍夫投票机制来估计目标位置。

1 核相关滤波跟踪算法

1.1 循环矩阵及移位过程

核化相关滤波器的高速跟踪（high-speed tracking with kernelized correlation filters，KCF），是目标跟踪领域一种经典的算法，具有很高的研究价值。该算法利用循环矩阵和离散傅里叶变换以及核方法解决了复杂的矩阵运算问题，提升了跟踪性能和相关滤波的鲁棒性［9］。

文献［5］利用岭回归去训练跟踪器。跟踪器在目标的中心位置将目标与周围的小部分背景选做跟踪窗口，得到大小M×N的样本图像块x。再对xi进行循环移位，i∈｛0，1，…，M-1｝×｛0，1，…，N-1｝，而每一个yi都对应于一个样本xi的高斯标签（正0负1）。设训练样本集为(xi,yi)，则其线性回归函数为f(xi)=ωT⊙xi。ω为列向量，表权重系数。ω通过最小二乘法求解：

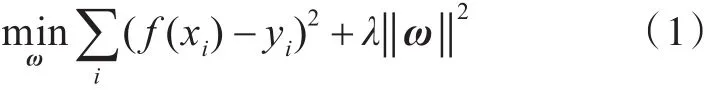
其中λ是控制过拟合的正则化参数，以保证分类器的泛化性能。⊙表示元素点乘。

该最小化目标函数在频域中有如下闭式解：

其中，XH为Hermitian转置，即XH=（X*）T，X*为X的复数共轭。

图1 一维向量得到的循环矩阵Fig.1 Cyclic matrix obtained from one-dimensional vector

对二维图像，可通过循环移动x轴和y轴实现不同位置的移动。因此由一个向量x∈Rn可通过不断地乘上排列矩阵得到n个循环位移向量，如图1所示。

再将这n个向量依序排列到一个矩阵中，就形成了X生成的循环矩阵C（X）。在傅氏空间中，任意的C（X）都能使用矩阵F来进行对角化：

其中F是离散傅里叶矩阵。表示矩阵X的第一行向量经过离散傅里叶变换后的值。循环移位得到的样本如图2所示。

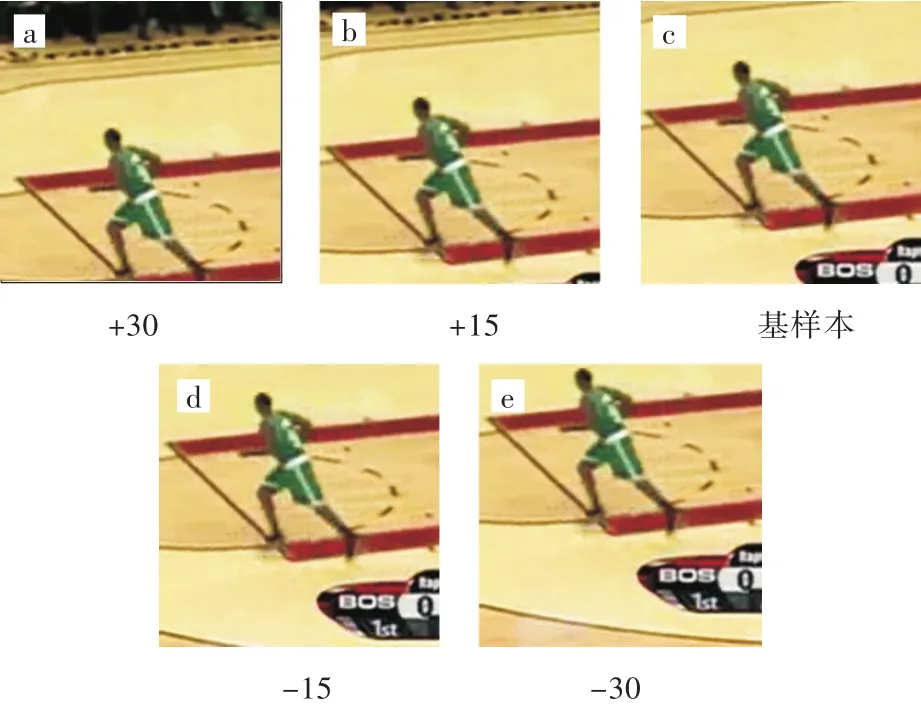
图2 二维图像经过不同行数的移位：（a）下移30行，（b）下移15行，（c）基样本，（d）上移15行，（e）上移30行Fig.2 Two-dimensional images shifting through different lines：（a）down 30，（b）down 15，（c）sample，（d）up 15，（e）up 30

1.2 滤波器系数及相关响应的求解

利用核方法，将线性问题的输入映射到非线性特征空间Φ（x）中。过程分为如下两步：

1）将解ω表达为样本的线性组合：。其中αi为ω的对偶空间向量，即滤波器系数。

2）用点积的形式来写入核方法：k(x,x')=φT(x')⋅φ(x)，该方法用核函数k（高斯或多项式）来计算。所有样本对间的点积保存在一个n×n的核矩阵K中，元素值为Kij=k(xi,xj)。

但核方法的缺点在于，回归函数的复杂性会随样本数目的增加而增加：

存在如下定理：给定循环数据C（x），对任意排列（置换）矩阵M，当核函数满足k(x,x')=k(Mx,Mx')，则对应的K为循环矩阵。而核化的岭回归的解为：α=(K+λ⋅I)-1y。其中K为核矩阵，α为系数αi的向量，对偶空间中的解。再像线性情况一样对角化上述方程，有其中kxx为核矩阵 K=C（kxx）的第一行的向量，yˆ为标签列向量的傅里叶变换。

很少单独对一个图像块来评估回归函数f（z）。为快速检测感兴趣物体，一般在若干图像位置上评估f（z），这些块可用循环移位来建模［10］。再用KZ表示所有训练样本与候选块间的核矩阵。而所有训练样本和图像块都分别为基样本x和基块z的循环移位。用循环矩阵的第一行向量来定义核矩阵：KZ=C（kXZ），由方程（4）可计算所有候选块的回归函数：f（z）=（KZ）T·α。其中f（z）为检测响应，包含了所有z循环移位的输出。

为了有效计算上述回归函数，结合上式并对角化f（z），有

2 优化搜索策略的改进算法

如1.1节所述，分类器在M×N的样本图像块x上训练，并以目标位置为每一块的中心。当训练结束后，对于后续帧，同样以上一帧目标位置为中心（预测区域），在大小为M×N的图像块z（patch）上检测并计算响应。检测的候选区域便是由上一帧的预测区域做循环移位得到的，如图3所示。通过密集采样可以提取出图像块的全部特征，优于只利用每个候选框的局部特征的随机采样。

图3 检测图像块：（a）随机采样，（b）密集采样Fig.3 Sampling of detected image patches：（a）random sampling，（b）dense sampling

虽然密集采样可以利用图像块的全部特征，但是信息冗余非常大，并且会降低搜索速度。由实验观察到，视频前后两帧中的两个目标区域块，其均值和方差应该最为接近。基于此提出了一种优化搜索策略，用于改进KCF算法的密集采样部分，以达到提高搜索速度，实现目标跟踪实时性的目的。

在第t帧中，由最大响应得到了目标的位置，该图像块大小为目标框加扩大1.5倍的padding窗口。其数据存放在二维数组中，数组的元素即为图像的像素。先将第t帧中图像块的均值和标准差记为μm和σm。而下一帧中，经循环移位的n个图像块的均值和标准差分别为：μ1,μ2,…,μn和σ1,σ2,…,σn。再把它们与μm和σm作比较，满足以下条件的图像块优先检测并计算响应：

手动选择阈值并测试数据集中的6个视频序列（Basketball，Bird2，Box，Car4，Freeman1，Girl），本文算法的平均跟踪帧率提升为10.1%～12.1%。然而，在实际跟踪过程中，多次手动设置阈值会影响跟踪效率，统一设置固定阈值又会降低算法的自适应性，使得跟踪准确度受到影响［11］。

为避免上述问题，本文将阈值设为能够使算法的平均跟踪帧率提升10%时的阈值大小。为求得该自适应阈值，需要先确定平均每帧所需的用于匹配的图像块个数。假设算法帧率提升达到10%时，平均每帧需要用到k（k＜n）个候选图像块用来跟踪并计算目标的中心位置。再依据最相似图像块间的均值和标准差的距离应最小的原理，这k个候选块取自排序队列中距离最小的前k个，其中，排序队列按照如下公式计算所得的距离大小进行排列：

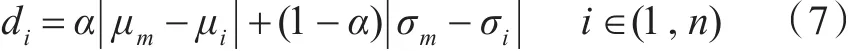
公式（7）中，di反应了当前帧中的图像块i与上一帧中的目标图像块m之间的均值和标准差的距离大小，α∈(0,1)为排序时分别赋予均值和方差的权重，当图像块的均值对跟踪结果的影响更大时，算法取α＞0.5，当图像块的标准差对跟踪结果影响更大时，算法取α＜0.5。将全部n个块都按上述公式算出值并按由小到大的顺序排序，那么，序列中的前k个距离所对应的k个图像块，即为算法在实际跟踪时用于匹配的k个图像块。后续n-k个块由于误差较大，因此舍弃不用。

设定平均帧率提升10%的情况下，可以确定每帧平均所需的匹配图像块个数k，在此基础上，阈值T1，T2可以通过上一帧目标中心图像块m与当前帧第k块之间的均值、标准差的差值得到。而且每个测试集由于图像的像素不同（720×400，576×432等）和面临的问题不同（比如遮挡、背景相似、尺度变化等），阈值会根据满足标准的μk、σk自动调整，达到自适应的效果。

3 结果与讨论

实验平台为Windows7 64位旗舰版系统和MATLAB R2014a软件，在笔记本电脑上进行了调试运行。CPU为英特尔酷睿i5-3210M@2.50 GHz双核，内存为 DDR3 1 600 MHz 4 GB［12］。

选取OTB100［13］上的6个具有挑战性的视频序列（Basketball，Bird2，Box，Car4，Freeman1，Girl）进行测试，并对比分析了实验结果。这些序列中的目标会受到诸如光照变化、快速运动、尺度变化、遮挡以及平面外旋转等多种复杂因素的影响。实验中改进算法的MATLAB源码是由作者公开的个人网站上获取的，可以保证实验数据的公正客观。

3.1 候选图像块数量的影响

实验首先测试了算法帧率是否会受到图像块数量的影响。将原文中用于扩展背景信息的pad⁃ding窗口由1.5倍目标框扩大倍数修改为0.5和1.0，再进行对目标候选区域的分块测试。实验结果表明改变padding大小对跟踪的精度并无显著影响，在3个视频序列上分为不同大小图像块的帧率如表1所示。

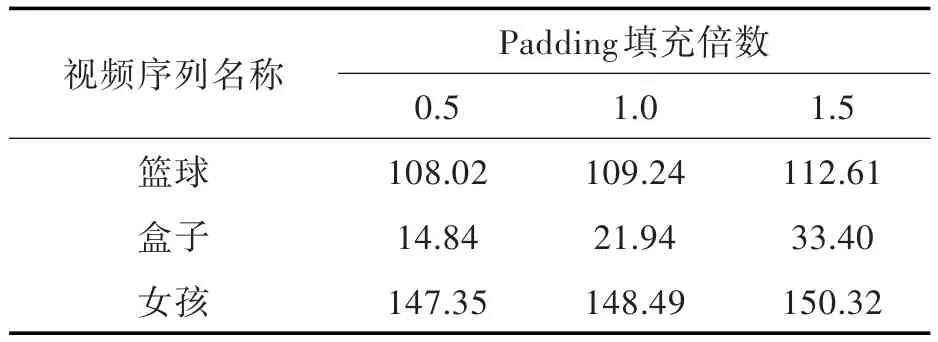
表1 不同padding大小下的算法帧率Tab.1 Algorithm frame per second performance at different padding sizes frames/s

从表1可得出padding越小时算法帧率也越小的结论。由于padding较小时会增加预测区域循环移位的次数，导致分块得到的patch数量增加，使公式（5）计算核相关的次数也相应地增加，因此算法的速度会稍微降低。本实验未对padding做更大值的测试，原因是分块尺度过大，搜索窗可能占满整个图像甚至超过原图像的尺寸，故无法对原图进行分块，也无法对目标进行跟踪。因此，padding为1.5倍大小时跟踪效果最显著。

3.2 不同算法对比分析

实验中控制过拟合的正则化参数λ设为10-4。高斯核条件下的σ为0.2。padding窗经过上述分析取1.5。k在Basketball序列中取13（总共40个），即前32.5%的图像块，在Girl序列中取11（总共24个），即前45.8%的图像块。自适应阈值T1和T2根据上述不同k值计算出的μk、σk自动调整时效果较好。

在MATLAB上选用距离精度作为衡量算法性能的指标，目标的中心位置误差（center position error，CLE）小于某一固定阈值时，符合的帧数与视频总帧数的比值即为算法精度。这里的阈值通常以20个像素返回精度。

图4的实验结果集成了改进算法OSKCF（Op⁃timized Searching Strategy for KCF，OSKCF）与较早的9种性能较好的跟踪算法，并横向对比了其中CSK、KCF、Struck［14］（structured output tracking with kernels，Struct）和检测学习跟踪［15］（tracking-learn⁃ing-detection，TLD）4种算法的性能。横坐标为目标误差像素阈值，以10像素为1个单位，纵坐标则表示算法精度。各算法曲线基本呈半梯形（左半部分）状，阈值在30像素后曲线基本不再增长，因此取20像素来计算阈值是合理的。

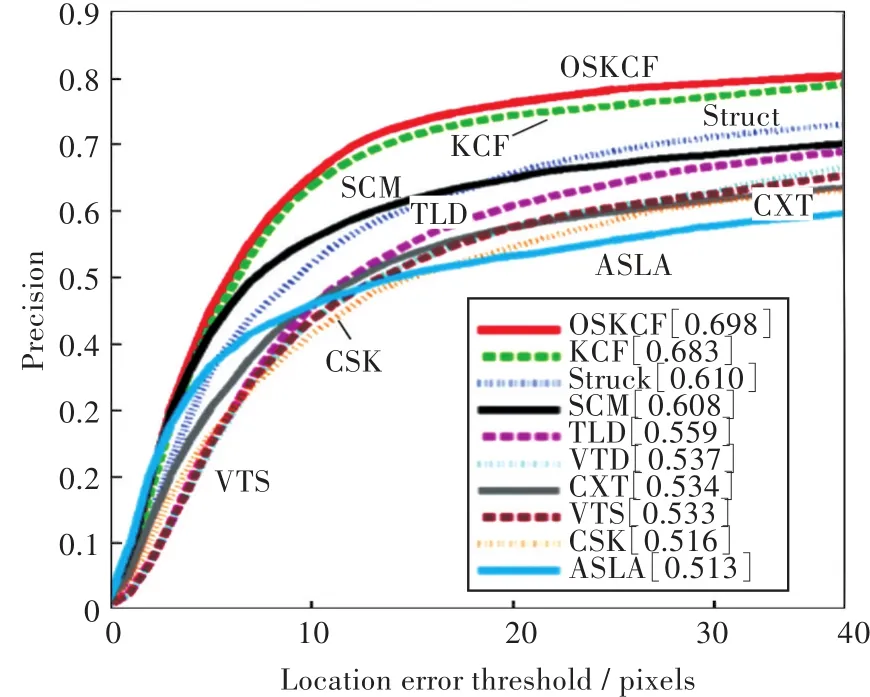
图4 不同跟踪算法的精度图Fig.4 Precision of different tracking algorithms

从图4可看出，经过优化候选区域的搜索策略并筛选图像块后，改进算法OSKCF的性能在较早的10个测试算法中最好，优于2012年以前最快的算法Struct以及经典的long-term算法TLD。在测试Basketball序列时，OSKCF平均精度为0.942，平均帧率为115.83帧/秒。而原KCF平均精度和帧率为0.923和103.34帧/秒，帧率提升达12.1%；测试Girl序列时，OSKCF平均精度和帧率分别为0.879和 157.67帧/秒，原 KCF分别为 0.864和143.25帧/秒，帧率提升10.1%。而测试其他几个挑战性更大的序列，涉及目标的快速运动及遮挡问题，精度较低只有50%左右。本算法的精度较KCF，Struct，TLD，CSK 分 别 提 升 2.2%，14.4%，24.9%，35.3%。测试6个视频序列的平均帧率如表2所示。

表2 算法在6个视频序列上的平均帧率Tab.2 Average frame rates of algorithms in 6 video sequences frames/s

经过分析，优化搜索策略后的OSKCF虽然对跟踪精度提升不大，但是可以明显提升原算法的帧率，从而使得目标跟踪算法的实时性进一步得到提高。

4 结 语

本文提出了一种优化候选图像块搜索策略的OSKCF算法，通过T1和T2这两个自适应阈值和最相似图像块间的均值方差的距离应最小的原理，选取排序队列中距离最小的前k个候选图像块，明显提升算法的FPS。实验结果表明，本文算法较原算法速度提升10%左右，性能较好，可满足大多数情况下的目标跟踪检测需求。但是在目标受到诸如光照变化、快速运动、遮挡以及平面外旋转等多种复杂因素的影响时，部分测试视频出现无法准确跟踪目标的现象。如何解决这些当前跟踪领域的一些共同难点，避免产生跟踪漂移等问题，将在未来的工作中做进一步研究。