基于非线性损伤理论的改进CVISC模型及其在FLAC3D中实现
2019-02-18文宝萍蒋秀姿李瑞冬
蒋 树,文宝萍,蒋秀姿,李瑞冬,赵 成
(1.中国长江三峡集团有限公司博士后工作站,北京 100038;2.中国地质大学(北京)水资源与环境学院,北京 100083;3.湘潭大学土木工程与力学学院/岩土力学与工程安全湖南省重点实验室,湖南 湘潭 411105;4.甘肃省地质环境监测院,甘肃 兰州 730050)
滑坡是斜坡岩土经历一定时间累进性变形破坏的结果。因此滑坡岩土变形破坏具有不同程度的流变特征,基于流变模型研究滑坡形成过程、预测滑坡活动趋势一直是国内外滑坡研究的热点和难点问题之一[1-4]。当滑坡以低速缓慢形式滑移或复活时,滑坡岩土变形破坏的流变特征尤为显著[1,3,5-6]。
岩土体流变本构模型构建有多种方式,包括基于试验数据拟合的经验模型[7],基于流变力学的解析模型[8]和基于黏弹塑性元件的元件模型[9]等。其中,元件模型因其物理意义明确、简单直观,在国内外研究中应用最广。元件模型研究中,将岩土流变特性看作是弹性、塑性和黏滞性叠加的结果,认为虎克弹性体、圣维南塑性体和牛顿黏性体三个基本元件能够表征岩土的弹性、塑性和黏滞性状,通过将三个三基本元件按不同方式进行组合,实现对岩土体各种流变行为的拟合及预测[10-11]。由于虎克弹性体和牛顿黏性体反映应力-应变速率的线性关系,所以这类元件的线性关系组合不能描述具有典型非线性特性的岩土蠕变破坏。于是,许多学者尝试将这些元件进行非线性组合建立反映岩土蠕变破坏性状的非线性流变本构模型。邓荣贵等[12]提出了应力与蠕变加速度成正比的非牛顿流体粘滞阻尼元件,将其与传统模型结合,实现对岩石加速蠕变的刻画。曹树刚等[13]用非牛顿黏滞体替代西原模型中与塑性体并联的牛顿黏滞体,提出了能够描述岩石蠕变三阶段的改进西原模型。然而,岩土变形破坏过程是内部微破裂逐渐积累过程,这些模型不能体现对岩土蠕变本质的刻画。损伤力学出现后,基于损伤力学原理构建能够反映岩土时效变形过程中损伤积累、裂纹扩展特征的流变本构模型成为流变力学研究的热点[14]。朱维申等[15]将周维垣等[16]针对节理岩体提出的损伤断裂模型与西原流变模型结合,研究岩质边坡变形破坏发展过程。肖洪天等[17]基于三峡船闸花岗岩的裂纹扩展试验,提出了裂纹流变扩展计算公式,以此为基础,建立了裂隙岩体损伤流变力学模型。周峙等[18]基于巴东组泥质粉砂岩的室内三轴试验,从Mohr-Coulomb准则出发建立了粉砂岩变形破裂全过程的损伤软化统计本构模型。然而,这些模型仅适合于裂隙岩质边坡的流变特征分析。目前针对滑坡岩土的非线性损伤流变模型在国内外研究尚较少涉及。
FLAC3D(Fast Lagrangian Analysis of Continua in 3 Dimensions)是由美国Itasca公司开发的、基于连续介质快速拉格朗日算法的有限差分数值模拟软件[19],内置Mohr-Coulomb、Drucker-Prager等25种弹塑性本构模型和CVISC、Burger等8种流变模型。Itasca公司在FLAC3D中提供了用户接口和所有本构模型的源代码,方便用户对软件内置本构模型进行修改和二次开发。CVISC流变模型是由Burger流变模型与Mohr-Coulomb塑性模型组合而成的元件模型,可以描述剪切状态下岩土流变特征,尤为适合模拟以剪切破坏为主的滑坡岩土蠕变行为。但是,该模型为基础元件的线性组合模型,只能描述滑坡岩土的减速蠕变和等速蠕变,不能刻画滑坡岩土的加速蠕变。若以CVISC模型为基础,基于损伤力学理论对其进行改进,建立描述滑坡岩土蠕变三阶段的非线性损伤流变模型;依照FLAC3D的代码规则,对改进模型进行二次开发,便可实现对滑坡岩土蠕变破坏全过程的数值模拟。
滑带是滑坡的控制单元,滑带蠕变特性控制滑坡变形破坏特征。本文以具有长期缓慢活动、并伴随间歇性剧烈活动特征的甘肃舟曲泄流坡滑坡为例,针对该滑坡滑带土的流变特征,在FLAC3D内置的CVISC流变模型中引入非线性损伤黏塑性元件,构建可描述滑坡加速蠕变过程的非线性损伤流变本构模型,通过FLAC3D开放的用户接口实现对本构模型的二次开发。通过对比改进前后CVISC模型对泄流坡滑坡的数值模拟结果,验证模型的有效性。
1 滑带土非线性损伤流变本构模型的建立
1.1 损伤变量与非线性黏塑性元件
大量研究证实,当应力水平高于长期强度时,岩土体将发生加速蠕变破坏[20-22]。加速蠕变破坏的实质是岩土内部损伤量变到质变的外在表现。这一过程可用非线性损伤黏塑性元件进行描述。依照损伤力学理论,岩土破坏的有效应力可定义为:
(1)
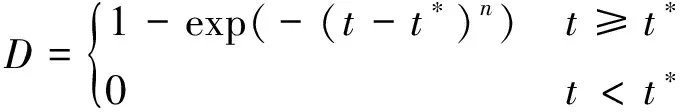
(2)
式中:D——岩土内部与黏性变形相关的损伤变量;
σ——应力;
t——流变时间;
n——与应变速率有关的常数,可通过拟合试验数据来确定;
t*——岩土进入非线性加速流变的起始时刻。
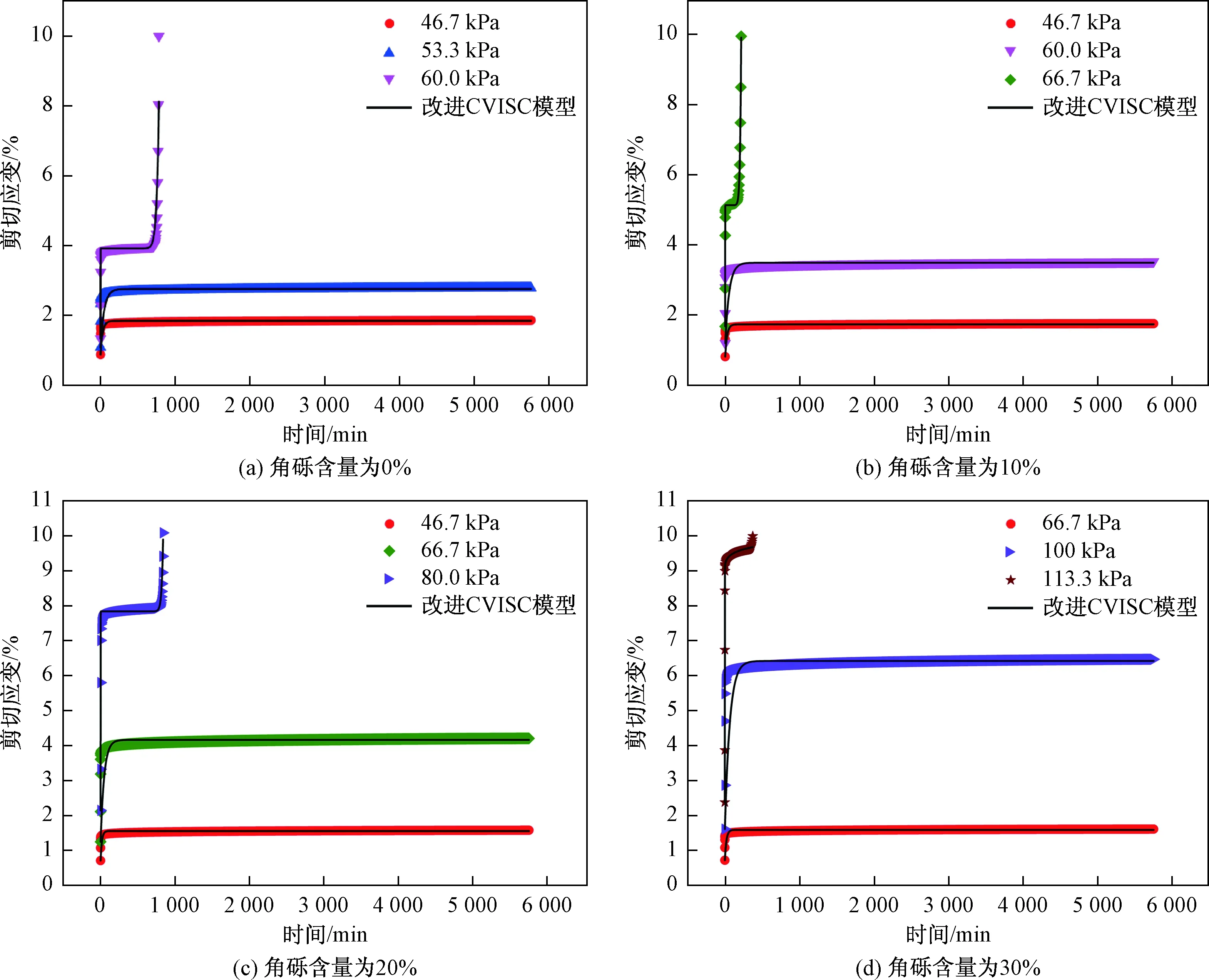
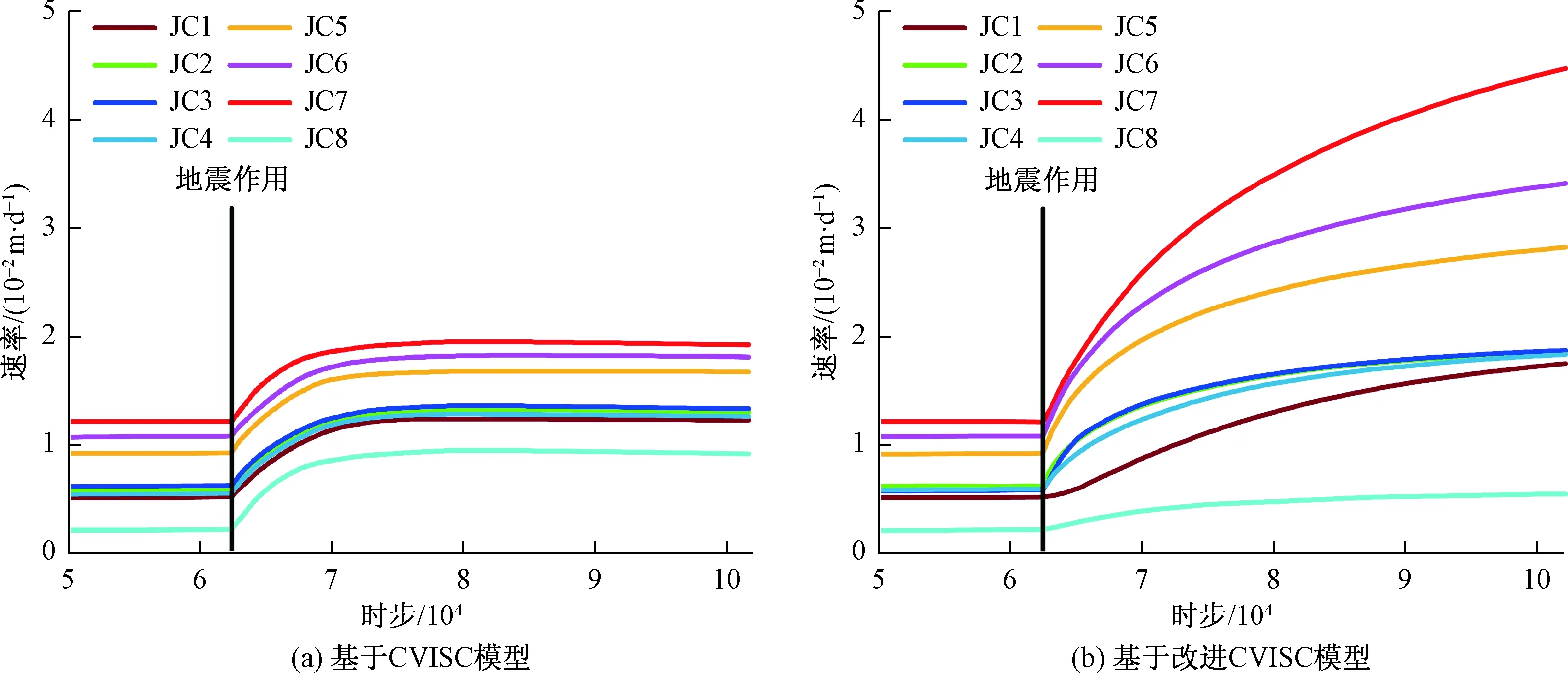
t 将含有损伤变量的黏性变形用非线性损伤牛顿体进行刻画。非线性损伤牛顿体与圣维南体并联,形成一个非线性损伤黏塑性元件。将这一元件与CVISC流变模型串联,可得到能反映蠕变三阶段、改进的CVISC非线性损伤流变模型。当应力小于长期强度时,非线性损伤黏塑性元件不起作用,模型退化为CVISC模型,可描述衰减和稳定蠕变两个阶段;当应力大于长期强度时,非线性损伤黏塑性元件则反映加速蠕变阶段应变随时间的变化关系。 一维应力状态下,改进的CVISC非线性损伤流变模型如图1所示。 图1 改进CVISC非线性流变模型示意图Fig.1 Modified CVISC non-linear rheological model 其中,模型第四部分为非线性损伤黏塑性元件,其余同CVISC模型。 当加载应力σ<σ∞时,模型退化为CVISC模型;当加载应力σ≥σ∞、t≤t*时,模型中非线性损伤变量不起作用。根据叠加原理,一维蠕变方程为: (3) 式中:EM,ηM——Maxwell弹性模量和黏滞系数; EK,ηM——Kelvin弹性模量和黏滞系数; ε,εP——应变和塑性应变; σ∞——长期强度; ηR——非线性损伤黏塑性元件黏度; 其余符号同前。 当加载应力σ>σ∞,t>t*时,模型各部分及损伤变量均起作用,则一维蠕变方程为: (4) 要实现将改进的CVISC非线性损伤流变模型应用于FLAC3D,需将改进的CVISC一维模型扩展成三维模型的差分形式。遵循Perzyna[8]提出的类比原理,可进行模型扩展。 σ<σ∞时,非线性损伤黏塑性元件不起作用,模型退化为CVISC模型,其三维差分本构方程已由相关文献给出[25]。在此,仅讨论σ>σ∞时非线性损伤黏塑性元件发挥作用的情形。此时,三维状态下总应变偏张量可写为: eij=(eM)ij+(eK)ij+(eP)ij+(eR)ij (5) 式中:eij——应变总偏张量,下标M、K、P、R分别代表Maxwell体、Kelvin体、Mohr-Coulomb体和非线性损伤黏塑性元件的应变偏张量。 Maxwell体三维状态下的偏应力-应变关系为: (6) 式中:Sij——应力偏张量; GM,ηM——Maxwell体的剪切模量和黏滞系数。 类似地,可得Kelvin体的偏应力-应变关系为: Sij=2ηK(eK)ij+2GK(eK)ij (7) 式中:GK,ηK——Kelvin体的剪切模量和黏滞系数。 对于塑性元件: (8) 式中:(eP)ij——塑性偏应变率; (eP)vol——塑性体的体积应变率偏量; δij——Kronecker符号; g——服从Mohr-Coulomb屈服准则的塑性势函数; λ*——仅在塑性流状态为非零参数,其值由塑性屈服条件所确定。 对于非线性损伤黏塑性体部分,当应力大于长期强度时,应变由非线性黏壶承担,有: (9) 式中:(eR)ij——非线性损伤黏塑性元件的应变速率偏量。 对模型整体有: σ0=K(evol-(eP)vol) (10) K——体积模量; evol——体积应变率偏量。 将式(5)~(7)、(9)、(10)写为增量形式,联立即可得改进CVISC模型的三维差分形式: (11) (12) (13) 式中:(SN)ij,(SO)ij——新、旧应力偏张量; Δeij,Δ(eP)ij,Δt——应变总偏张量、Morh-Coulomb体应变偏张量以及时间的增量形式; (eK,O)ij——Kelvin体应变偏张量的老值。 同理,式 (10)球应力的差分形式为: (σN)0=(σO)0+K(Δevol-Δ(eP)vol) (14) 式中:(σN)0,(σO)0——应力球张量变化率的新老值; Δevol,Δ(eP)vol——体积应变率偏量、塑性体体积应变率偏量的增量形式。 模型中塑性流动法则采用不相关联的M-C流动法则,当屈服函数f<0时,需根据塑性应变增量更新应力。 (15) 式中: 通过式 (11)和式 (14)计算的仅考虑黏弹性变形的新应力偏量和应力值; (SN)i,(σN)0——考虑塑性部分的新偏应力值和应力值。 将推导得到的非线性损伤流变本构模型三维差分形式、应力更新及修正公式,利用FLAC3D软件提供的本构模型二次开发程序接口,采用C++语言在Visual studio 2005平台上对CVISC模型源代码进行修改。修改数据项包括:初始化材料参数和关键求解函数,每一时步均调用一次求解函数,通过重载函数,根据子单元状态进行塑性判断与修正,并计算得到新的应力值,进而求得不平衡力、节点速率和节点位移。程序文件编写完成后,将自定义本构模型代码编译成动态链接库文件,在FLAC3D软件中调用该文件即可应用自定义本构模型。 泄流坡滑坡是我国著名的巨型低速滑坡,其活动特征具有典型的流变特性,因此将改进CVISC非线性损伤流变模型应用于该滑坡,以验证模型的有效性。 泄流坡滑坡位于甘肃省舟曲县白龙江下游约5 km处,发育在秦岭东西向构造带的光盖山—迭山蠕滑断裂带内[26]。滑坡南侧边界直接受蠕滑型活动断层控制,断层走滑速率和挤压速率分别为1.4 mm/a、3.7 mm/a[27]。滑坡平面上呈长舌状,纵长约2.6 km,平均宽度约550 m,滑坡体积约7 150×104m3。滑体物质主要为黄土状土以及灰岩、炭质千枚岩强风化碎石土,滑带物质为炭质板岩、千枚岩泥化后的黏性土(图2)。泄流坡滑坡活动历史近百年,1961年9月舟曲小型地震后和1981年4月9日暴雨后的2次剧烈活动,均堵断白龙江。该滑坡活动在时间上具有长期低速滑移、伴随间歇性强烈活动的特点,空间上具有分级分块特征[28]。 图2 泄流坡滑坡简化剖面图Fig.2 Cross section of the numerical model of the Xiliupo landslide 该滑坡的长期活动特性,表明其滑带强度已降至残余状态,因而其缓慢持续活动特征受残余状态下滑带土的流变行为控制[29]。蒋秀姿[30]对泄流坡滑坡滑带土残余状态下的蠕变行为进行了系统研究,发现当剪应力小于残余强度时,剪应变经过一段时间的减速增长后趋于定值,表现为衰减蠕变特征;当剪应力大于残余强度时,剪应变经过减速蠕变后进入加速蠕变阶段,直至蠕变破坏。据此,滑带土中微裂隙在加速蠕变过程中形成、并不断扩展,损伤积累直至蠕变破坏。因此,该滑坡滑带土在残余状态下的蠕变行为具有非线性损伤流变性质。 尽管遵循相同本构模型的滑坡具有相似的活动模式,但是模型参数刻画着各个滑坡间行为的差异。如前所述,滑带蠕变行为控制低速滑坡的活动特征。基于此,依据泄流坡滑带在残余状态下的蠕变曲线,拟合该滑坡的改进CVISC模型,从而获取模型计算参数。对于应力水平低于或超过残余强度的改进CVISC模型,分别采用未进入和进入加速蠕变阶段的曲线分别拟合。图3为不同颗粒级配下泄流坡滑带土试样的典型蠕变曲线与拟合的改进CVISC模型蠕变曲线。从图3可以看出,不同应力水平下改进的CVISC蠕变曲线与试验曲线拟合良好,由此获取的滑带模型计算参数列于表1。 图3 正应力400 kPa时不同角砾含量的泄流坡滑带土蠕变曲线拟合Fig.3 Fitting of the creep curves of the Xieliupo slip zone soil with different gravel content under the normal stress of 400 kPa 1960年2月3日舟曲5.25级地震促使滑坡变形加剧,1961年9月泄流坡滑坡中后部发生大规模快速活动[31]。为验证改进CVISC非线性损伤流变本构模型的有效性,基于改进前后的CVISC流变模型,对泄流坡滑坡进行地震工况下的三维数值模拟。采用拟静力法模拟地震工况,舟曲地处地震烈度Ⅷ度区,取对应的水平峰值加速度0.25g。 滑坡三维模型依据实测工程地质图和勘探资料建立(图4)。在断层位置设置界面单元,断层上盘设定速率边界条件,模拟断层作用。在地表设置8个计算监测点JC1-JC8(图4)。 图4 泄流坡滑坡三维数值模型及计算监测点Fig.4 3D numerical model of the Xieliupo landslide and the location of monitoring points 岩土体的基本物理力学参数均来源于室内试验测定,滑带流变力学参数通过前述改进CVISC模型与试验曲线拟合获得,每条曲线都可拟合出1组流变参数,得到流变参数随角砾含量变化的关系,再将滑带土实际角砾含量13.75%代入关系式中来确定初始流变参数。黄土状土以及风化碎石土层的流变力学参数则依 据经验值和滑带土的流变参数初步确定。运行模型后根据实际监测数据对初始流变参数调参,最终确定符合实际条件的参数如表1所示。 基于改进前后CVISC模型的数值模拟结果均显示,施加地震荷载前,各监测点活动速率恒定,滑坡整体处于稳定蠕变状态(图5)。施加地震荷载后,基于CVISC流变模型的模拟结果显示,各监测点的位移速率短期增加后,很快趋于恒定,表明地震作用造成滑坡活动速率加快,但并未出现加速蠕变,这与滑坡活动历史不符(图5)。基于改进的非线性损伤CVISC模型的模拟结果显示,滑坡中下部3个监测点JC2、JC3和JC4的位移速率增大一定幅度后趋于匀速发展,而坡脚处JC1点和中上部JC5、JC6和JC7点的位移速率经过前期缓慢增加后,呈现急剧增长趋势,量值达施加地震荷载前的2~3倍,反映滑坡中上部和坡脚处出现了局部大规模加速蠕变破坏特征,这与滑坡曾出现大规模分块滑移的历史基本一致。如此,证实了基于非线性损伤理论的改进CVISC模型具有较好的有效性。 表1 泄流坡滑坡流变计算参数 图5 地震工况下计算监测点速率-时步关系曲线Fig.5 Velocity curves of the monitoring points under the seismic condition (1)基于岩土蠕变破坏非线性特质和内部破坏不断积累特征,采用非线性损伤力学理论建立流变本构模型,较传统流变模型对岩土蠕变实质的刻画更为合理。通过引入损伤变量,将含有损伤变量的牛顿体与圣维南体并联,可以实现对岩土非线性损伤流变特性的刻画。 (2)FLAC3D内置的CVISC线性流变模型不能模拟岩土加速蠕变,串联非线性损伤黏塑性元件后,改进的CVISC模型能够模拟应力大于长期强度时的岩土加速蠕变。借助FLAC3D的开放接口,可以实现二次开发。 (3)甘肃泄流坡滑坡滑带土在残余状态下的蠕变特征具有典型的非线性损伤流变特性。通过对滑带残余状态下蠕变曲线的拟合,可获取改进CVISC模型的计算参数。基于改进CVISC模型的模拟结果与滑坡实际基本一致,证实改进CVISC模型具有较好的有效性。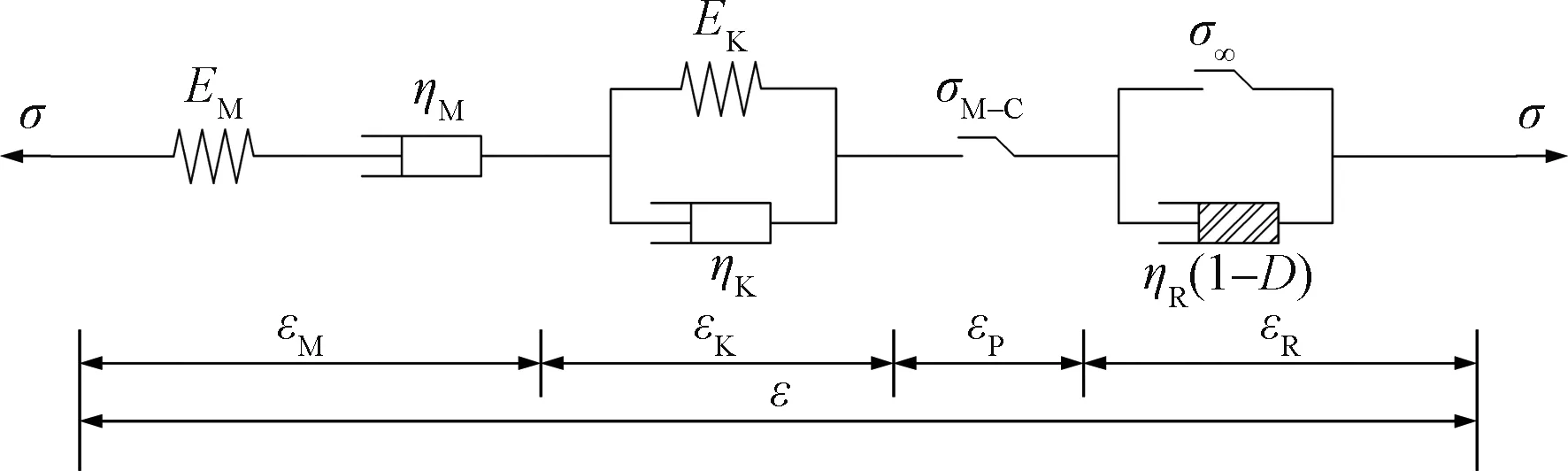
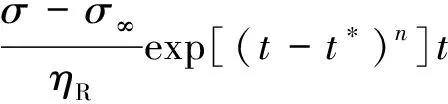
1.2 三维模型的差分形式及其在FLAC3D中的嵌入
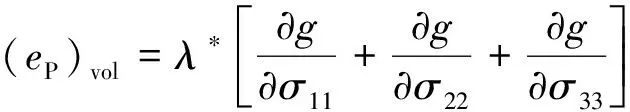
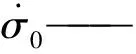
2 模型应用与验证
2.1 泄流坡滑坡概况

2.2 滑带土流变特征
2.3 改进CVISC模型的计算参数获取
2.4 基于改进前后CVISC流变模型的滑坡活动过程模拟


3 结论
