第二松花江干流傍河开采潜力评价
2019-02-18崔瑞娟冶雪艳杜新强王丽雪陆向勤
崔瑞娟,冶雪艳,2,杜新强,2,王丽雪,3,陆向勤
(1.吉林大学新能源与环境学院,吉林 长春 130026;2.吉林大学地下水资源与环境教育部重点实验室,吉林 长春 130026;3.济南市环境研究院,山东 济南 250102)
傍河水源地以其富水性强、埋藏浅、水量稳定、水质优良、易集中开采和便于管理等优点在许多国家普遍应用并成为重要的取水方式之一,国内外有大量的大、中型城市建立了傍河水源地,且傍河开采获得的水资源占总饮用水的比例逐渐增大。例如,瑞士约80%的饮用水来自傍河取水[1],法国、芬兰、匈牙利、荷兰、斯洛伐克傍河取水占日常生活饮用水的比例分别达50%、48%、40%、7%和45%[2],德国柏林有75%的饮用水来自傍河取水[3]。此外,印度[4-5]、埃及[6]和韩国[7]等国家傍河取水工程的应用也非常普遍。中国东北的一些城市在1930年就建立了一批傍河取水工程[8],目前中国大型傍河水源地已有300多个[9],仅沿黄河及其支流分布的省会城市和一些工业基地内就有约50个傍河水源地[10-11]。傍河取水主要通过激发并增大河水对含水层的入渗补给[10],以实现地表水与地下水资源的联合利用,通常情况下,傍河水源地所开采出的地下水资源量大部分来自于袭夺地表水资源量[11]。
第二松花江流域(丰满以下)是吉林省经济最繁荣、发展最强劲的地区,是东北地区主要的工业集中地和商品粮生产基地。吉林市、松原市等大、中城市工、农业生产和生活用水均以开发利用地下水为主,地下水供水占城市供水总量的60%左右[12]。由于区域整体上地下水资源并不十分丰富,研究如何通过傍河取水实现地下水与地表水的联合调度具有十分重要的意义。本次研究基于课题前期研究成果[12-13],在已筛选出的傍河取水适宜区内,设计合理的地下水开采方案,采用地下水数值模拟技术评价各傍河取水适宜区的地下水开采潜力。
1 傍河取水适宜性
1.1 研究区概况
研究区为第二松花江干流平原区,总面积约6 331.65 km2,河流全长约330 km。降水时空分布不均匀(图1),自东南向西北由约700 mm递减到约440 mm。降水量年内分布不均,主要集中在7—8月,降水量占全年降水量的70%~80%。多年平均蒸发强度自东部、东南部由1 200~1 500 mm 向西部、西北部增大为1 500~2 000 mm。

图1 研究区位置与降水量分布图Fig.1 Location of the study area and precipitation distribution
1.2 傍河取水适宜区域
王丽雪等[12-13]从水量、水质、地表水与地下水交互作用强度以及地下水资源开发利用条件4方面,建立傍河取水适宜性评价指标体系(表1),依据专家打分方法,制定各评价指标的权重及评分标准。根据建立的评价指标体系,通过相应指标的分数与相应指标权重的乘积加权求和得到傍河取水的适宜性指数(式1),根据傍河取水适宜性指数值,将评价区域傍河取水适宜性划分Ⅰ~Ⅴ共五个等级(图2)。其中,傍河取水适宜性等级为I~II级的区域,水质良好,满足生活饮用水要求,水量补给充足,地表水与地下水之间水力联系密切,傍河取水在水量和水质方面可靠保证,地下水资源开发利用条件适宜,为傍河取水的最优适宜区。
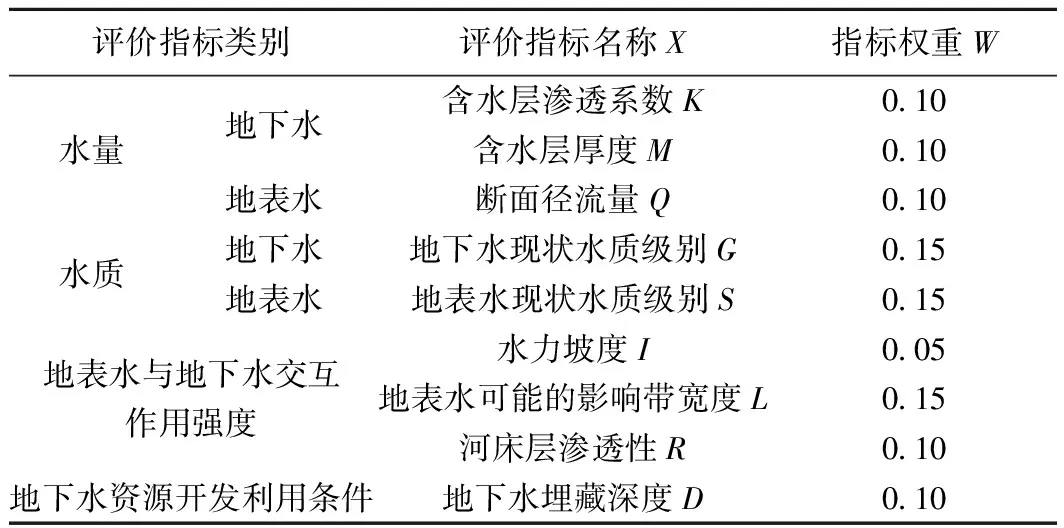
表1 傍河取水适宜性评价指标体系
A=XKWK+XMWM+XQWQ+XGWG+XSWS+
XIWI+XLWL+XRWR+XDWD
(1)
式中:A——傍河取水适宜性指数;
X——相应指标的分数;
W——相应指标的权重。
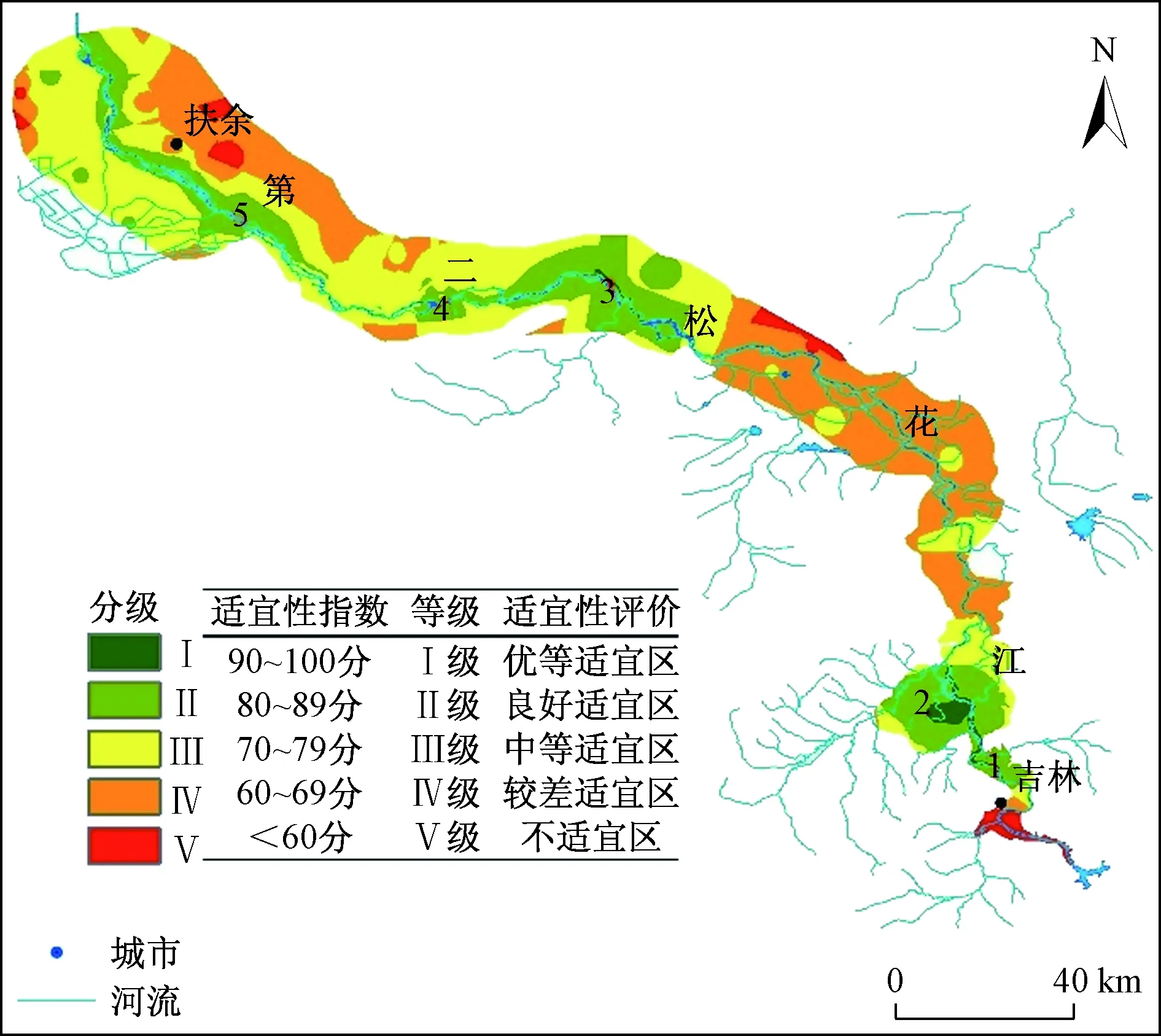
图2 傍河取水适宜性分区图(引用自文献 [12],有修改)Fig.2 Suitablity distribution of RBF
由图2可见,研究区内最优傍河取水适宜区共分为5部分,地理位置分布如下:吉林市龙潭区附近,吉林市下游段乌拉街附近,陶赖昭附近,黄鱼圈附近,靠近松原市。上述傍河取水适宜区普遍具有以下特征:含水层厚度较大、渗透性强;地下水位埋深相对较浅,接受大气降水入渗及地表水入渗补给的能力强;河床渗透性较好,有利于河水与地下水的水量交换。
2 傍河取水适宜区地下水流数值模拟模型
2.1 水文地质概念模型
2.1.1 边界条件概化
研究区外部边界全部概化为流量边界。其中,研究区西部边界AB、东北部边界BC为流域地表水资源二级分区界线,即分水岭,概化为零流量边界;西南部边界AC为山区与平原区的分界线,平原区地下水接受山区地下水的侧向径流补给概化为通用水头边界。研究区内部主要发育的第二松花江干流概化为河流边界(第三类边界条件)(图3)。
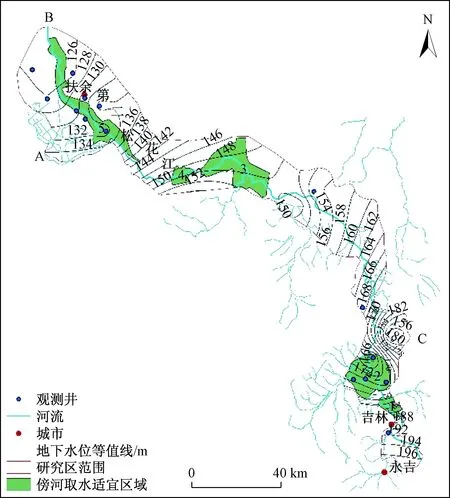
图3 水文地质概念模型图Fig.3 Conceptual hydrogeological model
2.1.2 含水层与水力特征概化
主要含水层为第四系松散岩类孔隙介质,主要由全新统沉积物组成,主要含水岩性为中粗砂及砂砾石,各地段富水性及水文地质差异较大,概化为非均质各向同性含水介质。第四系松散层厚度一般在10~50 m,其中第二松花江上游、中下游沿岸地段厚约50 m,伊通河及饮马河沿岸地段厚度约30 m。地下水天然水力坡度较小(约为0.4‰),地下水流可概化为符合达西定律的二维潜水非稳定层流。
2.2 数学模型
(2)
式中:K——潜水含水层渗透系数/(m·d-1);
μ——潜水含水层给水度;
H——地下水位高程/m;
B——含水层底板标高/m;
ε——源汇项/(m·d-1);
H0——初始地下水位/m;
q——边界上单位宽度的地下水补给(或排泄)量/(m·d-1);
K1——河床弱透水层渗透系数/(m·d-1);
m1——河床弱透水层厚度/m;
HR——河水位/m;
W——河流宽度/m;
x,y——坐标/m;
D——研究区范围;
t——时间;
n——法线方向;
Γ2、Γ3——二类及三类边界。
2.3 模型的识别与验证
基于适宜区内的观测井数据,分别选择时段2011年和2012年进行模型的识别与验证,研究区空间离散为11 014个计算单元格,单元格长为780 m,宽为737 m,每个单元格面积为0.574 km2。时间离散以5 d为1个时段,每个模拟期有69个时段。将模拟得到的观测井地下水位值及地下水位动态变化趋势与实际观测结果的一致性作为识别与验证的标准,得到识别与验证结果见图4、图5。
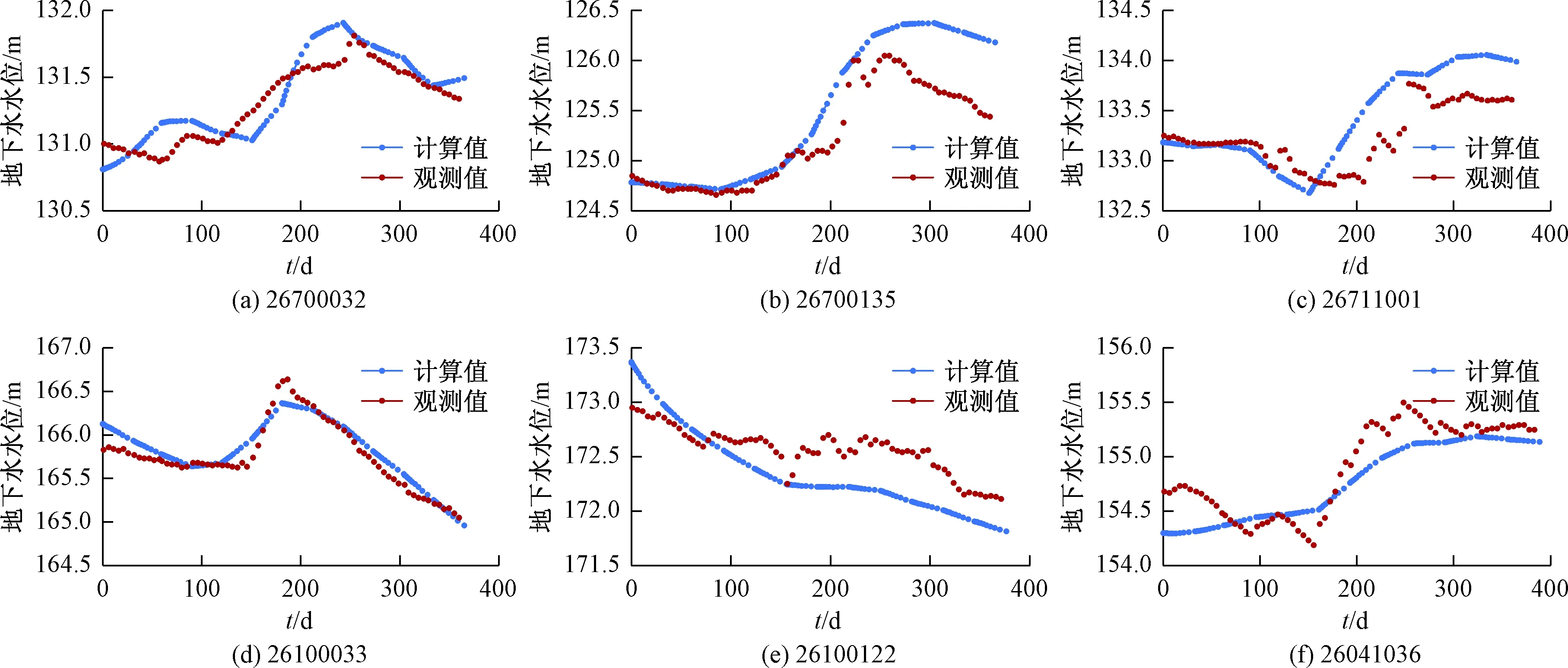
图4 识别期观测孔地下水水位拟合图Fig.4 Fitting curves of groundwater levels at the observation wells in the calibration period

图5 验证期观测孔地下水水位拟合图Fig.5 Fitting curves of groundwater levels at the observation wells in the verification period
由于模拟区域较大,识别和验证所用观测孔数量有限,为了进一步验证模型的可靠性,通过计算地下水存储变化量及地下水水量均衡对模型识别期与验证期的水量均衡状态进行验证[14]:
(1)利用Visual MODFLOW中的Zone budget模块统计地下水数值模型中的源汇项并计算水量均衡结果(表2);
(2)根据模拟期实测的地下水位动态变幅,计算地下水储存量的变化量:
(3)
式中:Qi——每个给水度分区在均衡期内含水层储存变化量/(104m3·d-1);
μi——给水度;
Fi——每个给水度分区的面积/m2;
ΔHi——每个给水度分区均衡期初、末刻的水头差/m;
Δt——均衡的时间周期。
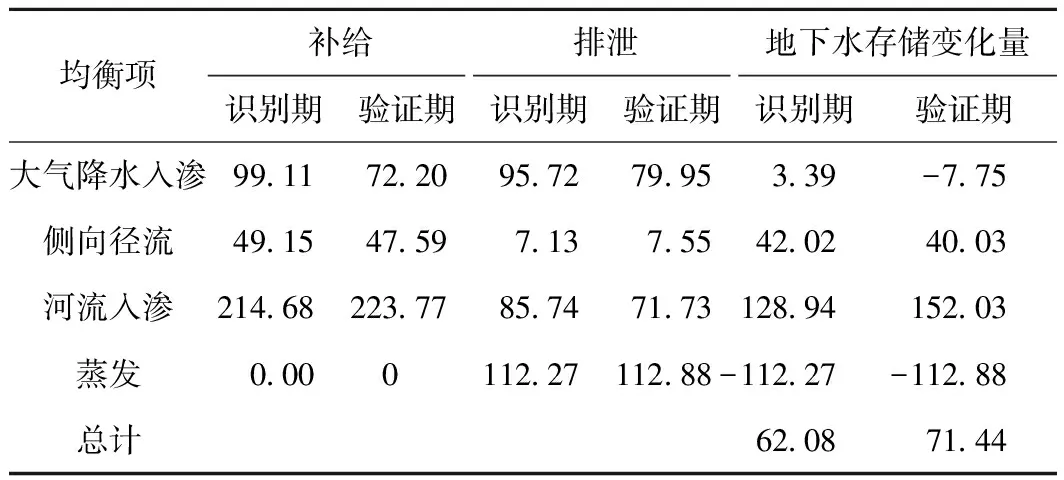
表2 基于数值模型的识别期(2011年)和验证期(2012年)水量均衡
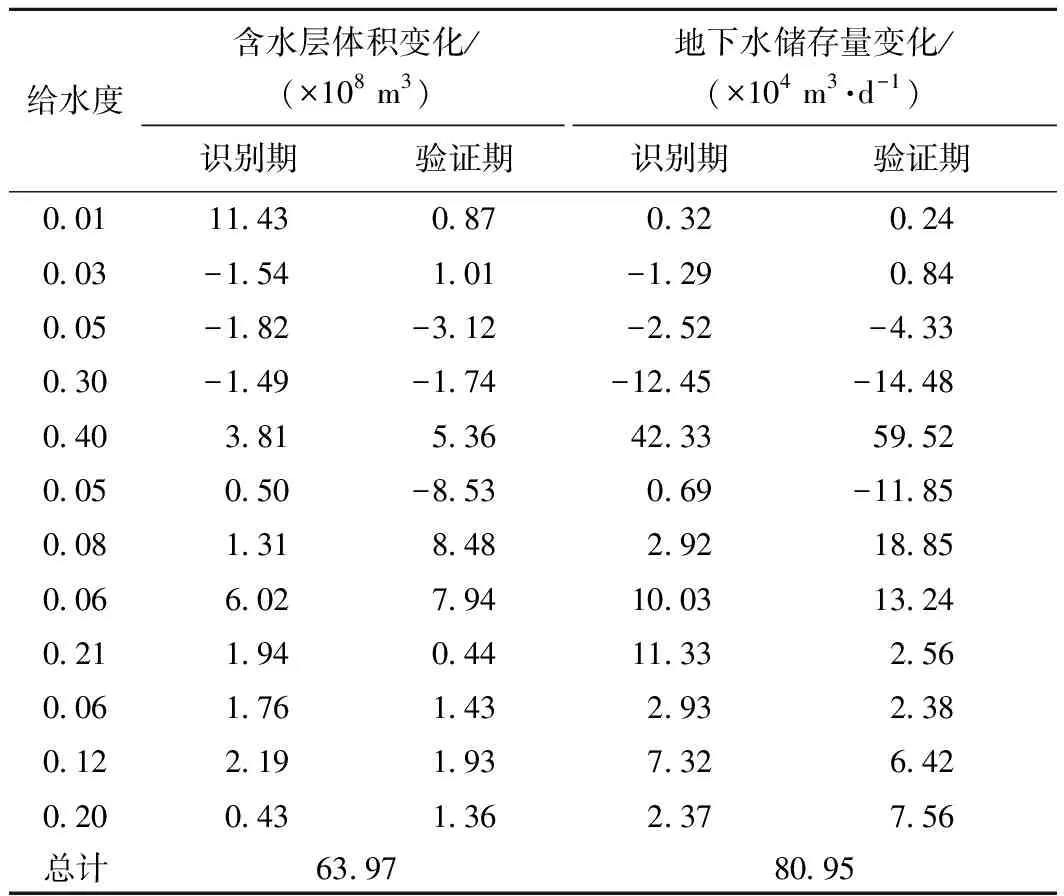
表3 基于观测数据的识别期(2011年)和验证期(2012年)地下水存储变化量
(3)根据研究区内地下水的补给项及排泄项计算得到模拟期内研究区的地下水均衡状态(表4)。研究区内的地下水补给项包括大气降水入渗补给量、灌溉回渗补给量、侧向径流补给量及河流渗漏补给量等,地下水排泄项包括地下水蒸发量、人工开采量、侧向径流排泄量及河流渗漏排泄量等。通过源汇项计算和统计,得到研究区在识别期与验证期的水量均衡表(表4)。
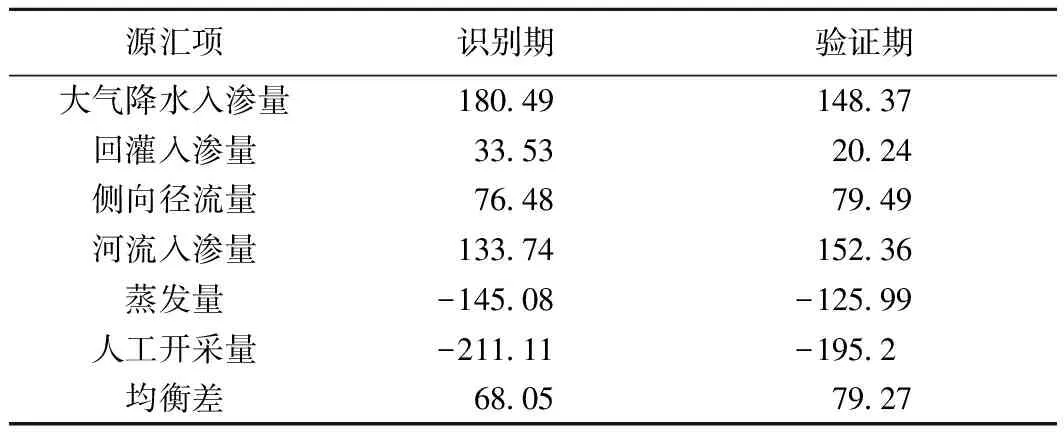
表4 基于源汇项计算的识别期(2011年)和验证期(2012年)地下水均衡量
采用基于地下水位动态观测数据计算得地下水存储变化量(表3)及基于源汇项计算得到地下水均衡结果(表4)与数值模型统计结果(表2)对比,验证所建模型的可靠性。由表2~4可知,在识别期内,基于数值模型的水量均衡差为62.08×104m3/d,基于实测地下位动态的含水层存储变化量为63.97×104m3/d,基于源汇项计算的水量均衡差为68.05×104m3/d,两种水量均衡方法与基于数值模型的水量均衡相比,均衡状态一致,均为正均衡,且均衡差量的相对误差较小,验证期也体现了相同的情况,可以证明建立的地下水数值模型在水量均衡的计算方面是合理、可靠的。
综合地下水位动态拟合以及水量均衡状态的验证,可进一步说明:本文所建立的地下水流数值模型对含水层结构、边界条件的概化、源汇项的处理及水文地质参数的选取较为合理,能够真实反映含水层的特征,可用于预测研究区地下水动态变化规律。
3 傍河开采潜力评价及影响分析
3.1 地下水允许开采量评价

图6 傍河取水各适宜区流场图Fig.6 Groundwater flow field in the suitable areas of RBF
在没有特别明确的生态水位指标情况下,通常将含水砂层厚度的1/3作为潜水地下水位降深的约束条件[15]。以往研究中通常将平均含水层厚度作为计算基础,得到一个统一的水位降深值,这显然与真实地下水流场有出入,据此评价的地下水允许开采量也显得粗略。因此,本次研究以现状地下水流场为基础,按计算单元减去1/3的含水砂层厚度值,得到傍河取水适宜区允许降深下的曲面流场(图6);本次研究中考虑到实际生产实践中在5个适宜区同时建立傍河水源地的可能性较小,因此对5个傍河取水适宜区段分别进行单独模拟,通过在适宜区域内均匀布设抽水井,尽量使各开采井横向、纵向间距相等,井间距约为1.5 km,根据研究区水文地质条件及地下水利用强度采用试算法调整开采井位和单井开采量,使预测流场与现状年允许降深条件下的流场尽量接近(图6f)。由于各适宜区面积不同,因此开采井数有所差别,最终在适宜区1~5内分别布设开采井数46、239、316、51和273眼,并得到各傍河取水适宜区的地下水允许开采量(表5)。需要说明的是,本次设计的井间距和井数量仅为能够得到预期流场分布形态的一种模拟方案,实际布井时需要结合抽水试验等资料进行调整。
3.2 开采潜力评价
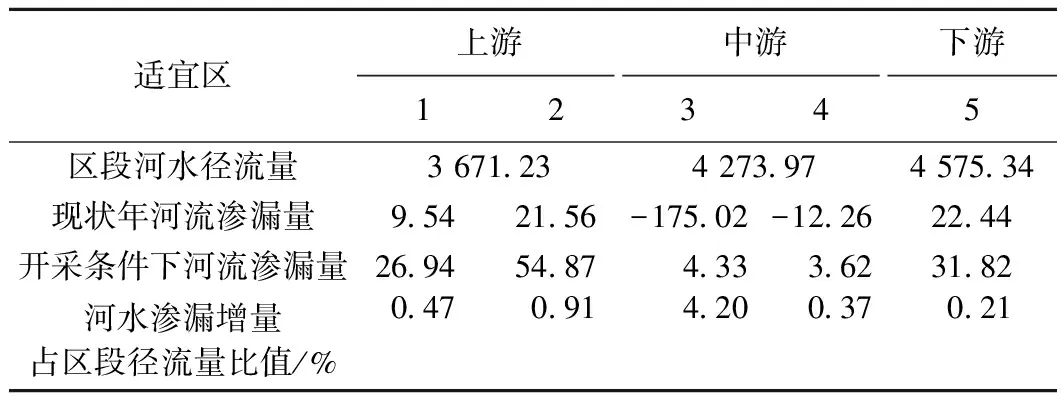
地下水开采潜力可依据地下水开采潜力指数p及可增开采资源模数q进行评价[16],p>1.2表示开采潜力较大,0.8 表5 各傍河取水适宜区地下水允许开采量 (4) (5) 式中:p——地下水开采潜力指数; q——地下水可增允许开采模数(×104m3· km-2·a-1); Q可采——地下水可开采资源量/(×104m3·a-1); Q开采——地下水已开采资源量/(×104m3·a-1); F——评价区面积/km2。 表6 适宜区开采潜力评价 由表6可见,5个傍河取水适宜区的地下水开采潜力指数p最小为3.70,大于1.2,表明适宜区均为有开采潜力区,且5个适宜区中4个开采潜力较大,1个开采潜力中等。说明各傍河取水适宜区开采潜力较大,可作为区域未来的供水水源地。 傍河开采条件下,适宜区1、2地表水与地下水的补排方向未发生改变,为地表水补给地下水,但补给强度较现状条件明显增大;适宜区3、4,现状条件下以地下水补给地表水为主,傍河开采条件下变为局部近河地段地表水补给地下水,但总体上的补给强度已超过地下水向地表水的补给强度;适宜区5总体补排方向未发生改变,为地表水补给地下水,但补给强度明显增大。 表7 傍河开采条件下河道侧渗量计算 一般认为多年平均径流量的10%是河道生态流量的最低下限,低于该值,河流生态系统健康得不到保障,河流生态环境功能将遭到破坏[17-18]。由表7可知,傍河开采条件下,各适宜区河流侧渗量占多年平均径流量的比值最大仅为4.20%,因此,在本区内按上述允许开采量进行傍河取水,对河流生态环境功能不会产生不利影响。 (1)本文采用地下水流数值模拟方法,以地下水水位降深不大于含水砂层厚度的1/3为约束条件,基于平均布井的试算法调整预测流场并使其与允许降深下的流场相拟合,确定了多年平均条件下各适宜区的地下水允许开采量。 (2)基于地下水流数值模拟模型的分析,傍河开采对地表水与地下水转化方向和转化强度有不同程度的影响,袭夺水量占河道多年平均径流量的0.21%~4.2%,不会对河道生态功能产生不利影响。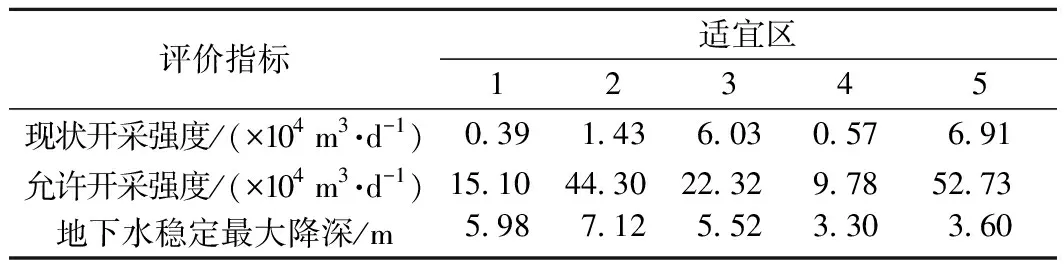

3.3 傍河开采对地表与地下水资源转化关系的影响
4 结论
