基于插值法的浮标优化布放

张 丹，时 光，余义德，王红萍

(1.中国人民解放军91550部队，辽宁 大连 116023；2.海军大连舰艇学院，辽宁 大连 116018)

0 引言

声纳浮标具有使用方便、隐蔽和受地域限制小等优点，是航空声纳搜索水下目标的首选[1-2]。声纳浮标搜索目标一般在已知有目标活动的概略信息条件下进行应召搜索。既为了取得好的搜潜效果，又要考虑节省浮标，正确地选择搜索阵形是反潜机使用声纳浮标需要考虑的重要环节，通常用一定搜索时间内的搜索概率来衡量阵形的优劣[3-5]。文献[6-8]基于蒙特卡洛方法，分析了不同参数对声纳浮标搜索效能的影响，但是并未给出不同阵型如何进行参数优化选择，且都未考虑目标航向变化的情况。应召搜索条件下，通常目标初始概略位置服从圆正态分布[9-10]，在搜索过程中目标、目标航向未知[11-12]，也可能采取变向规避运动[13-14]。文献[15-16]针对航向不变的简单扩散运动目标的情况，提出了搜索扩散运动目标的定量计算方法。本文针对目标航向不变和航向多次改变的情况，建立了浮标探测概率数学模型，基于牛顿插值算法，给出了圆形阵布阵半径优化选择方法。

1 扩散运动目标的搜索概率计算

设在一定海区Q，一批次投放N枚声纳浮标搜索单个目标。假设目标初始状态服从圆正态分布，目标运动方式为匀速直线运动，速度为v，航向在(0，2π]内均匀分布，t时刻目标位置为X(t)。B表示(0，t)之间目标被搜索事件，定义目标不被搜索概率为b(x，t)：

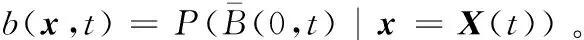
(1)

搜索密度为γ(x，t)，

γ(x，t)Δt+o(Δt)=P{B(t，t+Δt)|x=X(t)}。

(2)

对于多个相互独立的搜索器[17-18]：

(3)

对于b(x，t+Δt)，结合式(3)有

(4)

式(4)可转换为：

(5)

解微分方程得

(6)

设目标位置分布概率为ρ(x，t)，在时间t内累积探测概率P(t)为：

(7)

设ρ0(x)为目标初始概率密度，对于θ航向，t时刻不被搜索概率pθ(x，t)为：

(8)

则在时间t内累积探测概率P(t)为：

(9)

若目标多次改变航向，设搜索从T1开始，每Δt改变一次航向，共改变n次，搜潜概率计算公式为:

P(T1+nΔt)=1-Q(1)Q(2)…Q(n)。

(10)

Q(i)为(T1+(i-1)Δt，T1+iΔt)之间不被搜索的概率。

初始不被搜索概率密度为：

(11)

(12)

对于Q(2)，初始不被搜索的概率分布为：

p(x，T1+Δt)=p(x，T1+Δt)/Q(1)，

(13)

以此类推计算Q(n)，即可计算得到。

2 基于插值法的浮标优化布阵

若初始定位误差服从截尾圆周正态分布，航向未知条件下通常采用圆阵搜索。若可供投放的浮标数确定，阵半径成为唯一需要确定的参数，显然阵半径过大和过小均不利于搜索，肯定存在一个最优半径。通过计算若干阵半径对应的探测概率，然后采用插值法进行曲线拟合，从而提取最优阵半径，另外对于后者虽然航向改变次数对探测概率也有影响，但仍然可用插值法求解最优阵半径。

2.1 目标航向不变的最佳圆阵获取

假设目标初始状态服从圆周正态分布，匀速直线运动，航向在[0，2π)服从均匀分布。根据目标分布以坐标原点为对称中心，此时布放圆阵较为适合。对于浮标圆阵布放如图1所示，R为圆阵半径，d为浮标作用距离半径，浮标均匀分布在半径为R的圆上。

图1 圆阵示意

仿真参数：声纳浮标个数n取4，8，12；目标运动速度u=6 kt；初始圆周正态分布的标准差σ=20 nm；浮标有效作用距离d为4 nm或10 nm。搜索延迟时间T1和搜索持续时间T2-T1分别为4 hr和6 hr。对于每种参数n，u，σ，d的组合，计算搜索概率并用插值法得到圆阵半径与搜索概率的关系曲线，从而获得最优圆阵半径。不同参数组合下圆阵的最优半径R*和搜索概率P*(T2)如表1所示。由表1可知，航向不变目标进行搜索，使用4个声纳浮标，其中每个声纳浮标的搜索范围是10 nm，与使用12个声纳浮标，其中每个声纳浮标的搜索范围是4 nm所起的作用大致相同。

表1 最佳圆阵半径

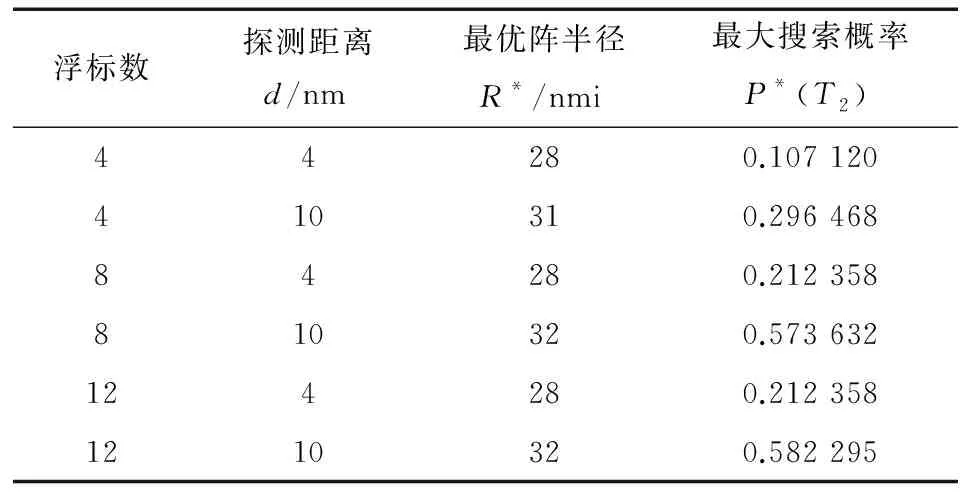
浮标数探测距离d/nm最优阵半径R*/nmi最大搜索概率P*(T2)44280.107 120410310.296 46884280.212 358810320.573 632124280.212 3581210320.582 295

对于T1=4 hr，T2=7 hr，目标速度12 kt，浮标探测半径10 nm，标准差为20 nm，不断改变圆阵半径，相应概率曲线如图2所示，可见R=56 nmi时，探测概率最大0.341 2。图3描绘了这种情况下不被搜索的概率密度分布，区域颜色越深，搜索不成功概率越大。

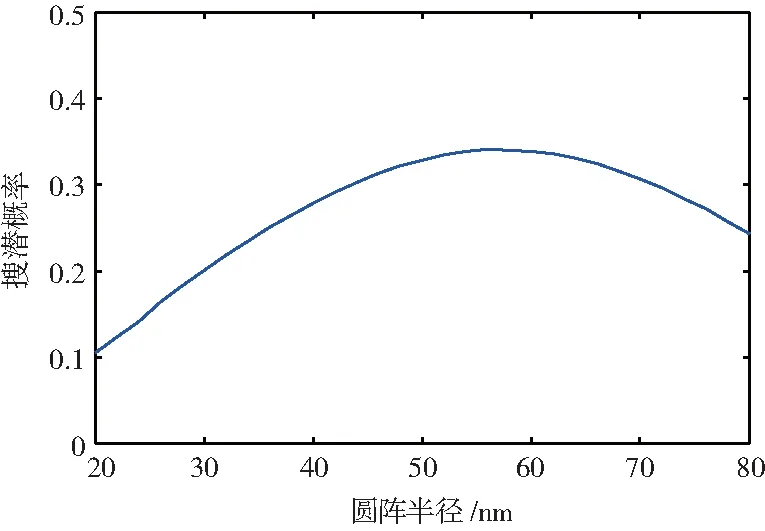
图2 浮标圆阵半径与搜索概率的关系

图3 目标不被搜索的概率密度分布

2.2 目标航向多次改变的最佳圆阵获取

假设目标的运动在每个Δt时间单元目标都会随机选择一个新方向。在t=0时，目标的分布为圆形正态分布；t=T1时，目标选择一个新的方向，试图避开探测，并且每个Δt时间单元继续选择一个新的方向。

表1中的第4种情况，8个声纳浮标的最佳圆形模式的半径R*=32 nm。保持其他的输入不变，航向在[T1，T2)内变化m次。对于圆形阵，计算Pm(T2)。在m=0时，Pm(T2)的值是在最佳圆形阵条件下目标以随机航向匀速运动条件得到的搜索概率。对于m=0，1，…，6，Pm(T2)>P0(T2)=0.573 626，目标通过数次改变航向，试图避开检测。目标航向改变次数对搜潜概率的影响如图4所示，仿真结果表明在时间间隔[T1，T2)内任意次的方向改变对搜索概率影响较小(即对于所有的m>7，|Pm(T2)-P0(T2)|<0.05)。

图4 目标航向改变次数对搜潜概率的影响

对于表1中情况4条件下，m=6时，圆阵半径与搜索概率的关系曲线如图5所示。该条件下最佳圆阵半径为29 nm(0.598 529)，而对于m=0时，最佳半径为32 nmi(0.573 632)。

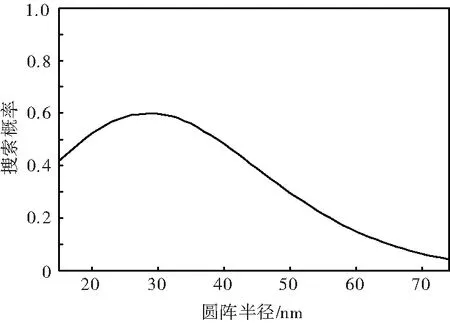
图5 圆阵半径与搜索概率的关系(m=6)

3 结束语

以上论述均假设初始状态服从圆周正态分布，目标所有航向上均匀分布，这时用规则的圆阵能达到较好的搜潜效率，该条件下只改变了一个阵形参数。如果有更确定或不同的先验信息，如目标某航向范围内均匀分布，这时最佳阵形并不好找，阵形参数增多，此时曲线拟合不再适用，需要合适的智能搜索算法，如模拟退火算法、进化策略和遗传算法等。