道岔尖轨段打磨目标廓形优化研究
2019-02-15宗聪聪周云飞丰灿灿
宗聪聪 张 让 周云飞 沈 钢 丰灿灿
(1. 吉林省(水利厅)河务局,130022,长春; 2. 同济大学铁道与城市轨道交通研究院,201804,上海; 3. 吉林省发展和改革委员会,130051,长春//第一作者,科员)
道岔是轨道交通中一个特殊的部件。其转辙区和辙叉区在运行一段时间后,磨耗损伤较严重,会降低车辆的行车安全性[3],故需对钢轨进行打磨。日本于1985年基于轮轨接触点分布提出了一种针对日本东海道新干线钢轨打磨的方法。文献[4]对新设计的钢轨型面进行了局部优化,使新设计的钢轨与实际线路更加契合。文献[5]从轮轨型面匹配角度优化钢轨的型面,降低了轮轨间的磨耗。本文运用文献[5-6]提出的轮轨最小法相间隙法的定义方式及对其最小值求解的数学方法,在进行一定改进的基础上优化道岔区钢轨型面。
1 模型
车辆运行过程中,其轮轨接触点附近的面法向间隙的平均值越小,则有效接触面积越大,车辆在道岔发生脱轨的可能性就越低[6-9]。
本文在计算中作出如下假设:① 当车辆在道岔转辙区内行驶时,轮轨为刚性,忽略弹塑性变形的影响,认为轮轨间只存在单点接触;② 轮轨接触点从基本轨跳跃到尖轨的过程中,存在2点接触,但这2点接触只是一个瞬态的过程,对求解不做考虑;③ 轮对的摇头角取值为0;④ 因为列车过道岔转辙区的横移量在一定的范围内徘徊,故优化前对横移量的范围进行预估计。
1.1 优化范围的选取
道岔转辙区钢轨由基本轨和尖轨两部分组成。通常情况下,只需保证优化范围稍大于接触范围即可。优化范围如图1所示。图1中,A和B表示基本轨优化区域的两端点,C和D表示尖轨优化区域的两端点。区域内坐标点横向固定,竖向可动。尖轨优化范围边缘不可太靠近尖轨与基本轨贴靠处,以避免法向间隙的骤增或骤减。
1.2 轮轨最小法向间隙法
在某个横移量xw下,轮轨接触点处的法向间隙求解图如图2所示。在接触点K的切线范围内,选取E、F两点距接触点距离分别为C1和C2,C1与C2值应略小于轮轨接触斑的短轴值。以接触点的法向,按照等间距进行直线分割(如图2所示),当分割密度取得足够大时,便可近似得到在该位置处的轮轨法向间隙值dki(i=1,2,3,…,m)。dki的平均值Dk即为在某横移量下轮轨对应的平均法向间隙值,即:
(1)
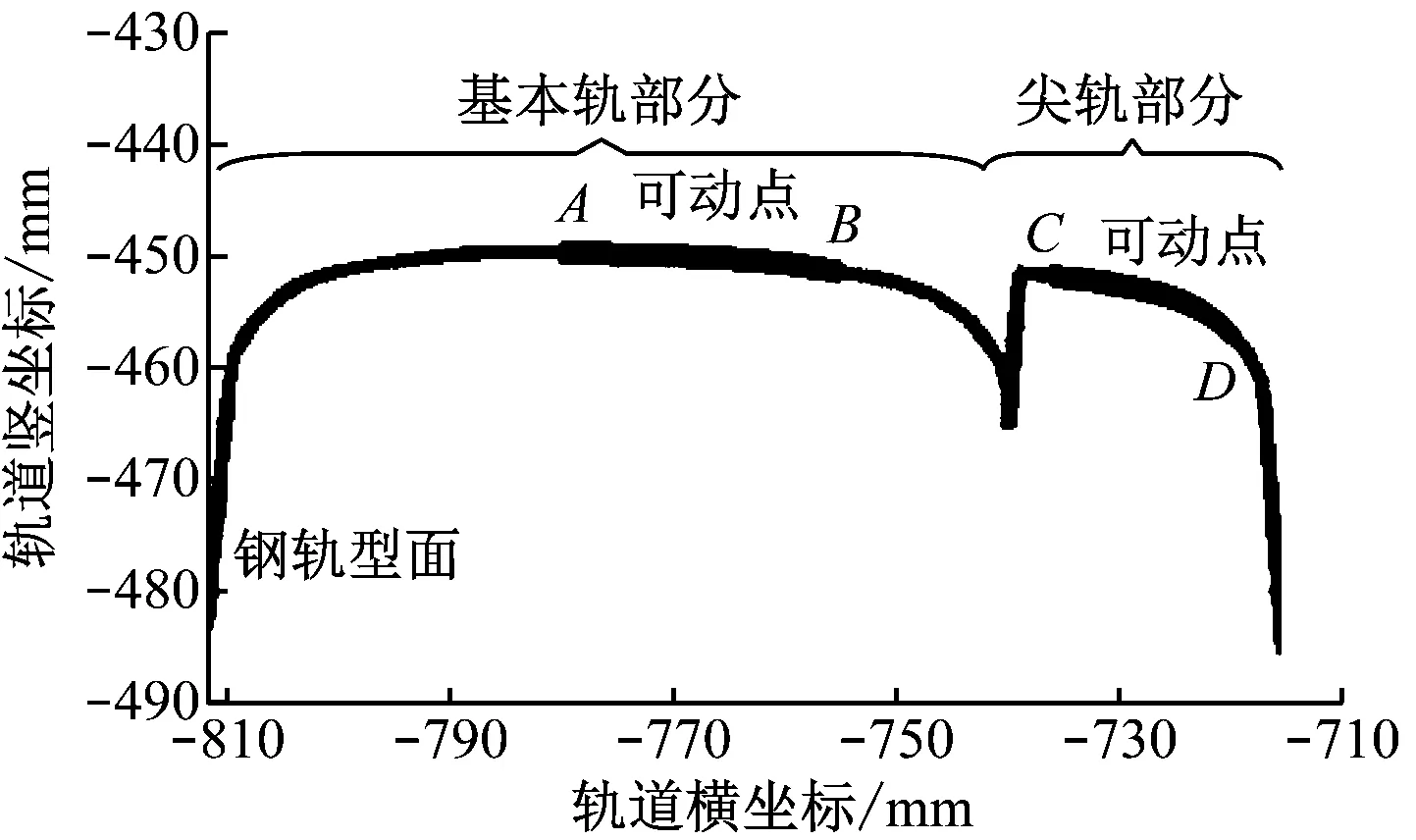
图1 优化范围示意图
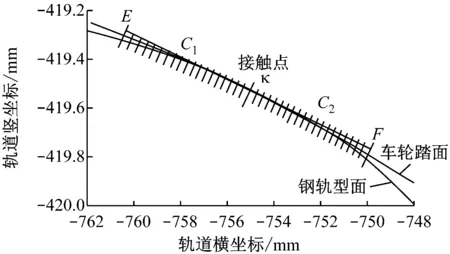
图2 轮轨接触点处的法向间隙求解图
将轮轨法向间隙值曲线与横轴的面积值S作为求解的目标函数,即:
(2)
式中:
j——对应的平均间隙值个数;
h——每次轮对横移的步长。
采用3次样条曲线进行进一步拟合,然后利用插值法,以获得平顺的优化点。优化之后的钢轨型面必须在原型面的下方[8],其约束式为:
(3)
式中:
Gi——第i点处的约束方程;
yi——第i点处的纵坐标值。
对于第i点处的上下边界值,有:
Ai≤yi≤Bi
(4)
式中:
Bi——原廓形的位置;
Ai——可以变化的区间范围,通常参照打磨车的最大磨削量。
利用SQP(序列二次规划)方法[12]进行求解。轮轨最小法向间隙法具体流程如图3所示。
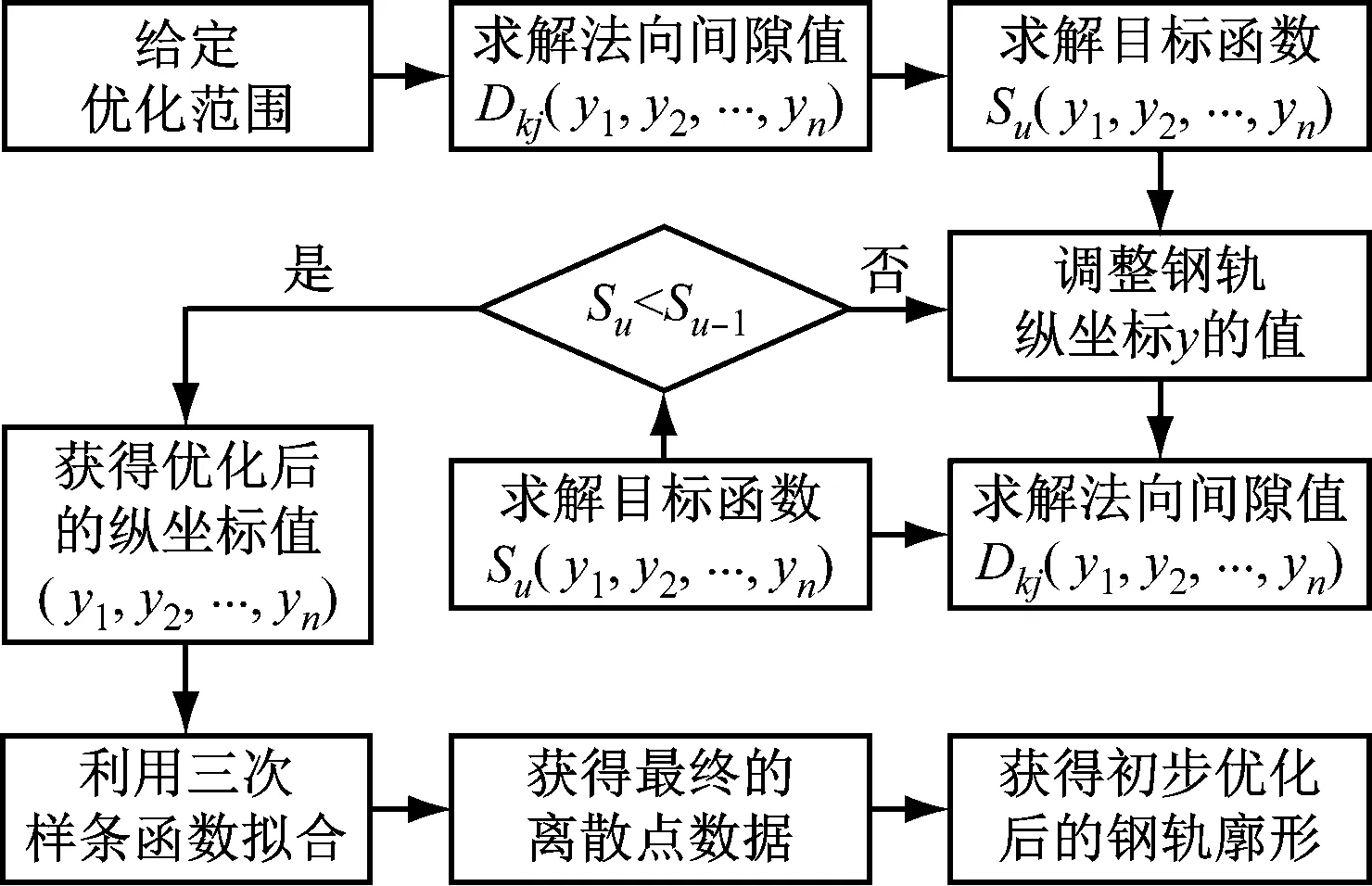
图3 最小法向间隙法流程图
2 试验验证
以LM型车轮踏面和60 kg/m轨右侧单开道岔为例,设行驶轨距为1 435 mm、轨底坡度为1/40、车轮名义滚动圆半径为420 mm,对关键的截面点进行优化分析。跳跃点定义为:当横移量发生微小改变时,轮轨接触点从基本轨跳跃到尖轨,而跳跃点横向间距为车轮踏面上跳跃点之间横坐标之差的绝对值。道岔钢轨打磨目标廓形计算流程如图4所示。
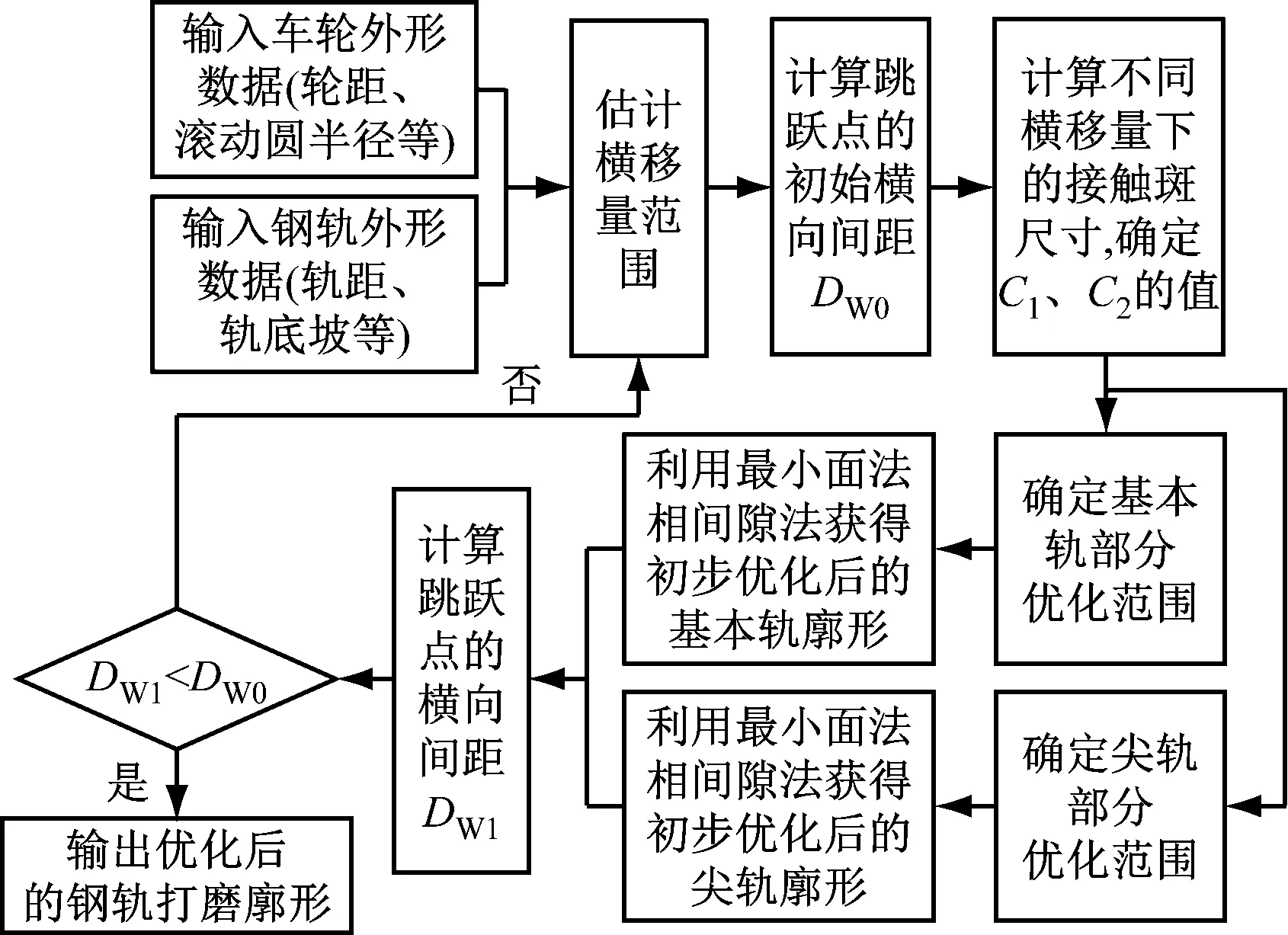
图4 道岔钢轨打磨目标廓形计算流程图
优化后轨辙区中端的钢轨廓形如图5所示。轮轨间平均法向间隙值如图6所示。试验结果表明:优化之后的轮轨间平均法向间隙值变小,在轨顶接触部分降低明显。在整体范围内,轮轨平均法向间隙值下降约1.3%。在同一轮重的情况下,钢轨廓形优化能有效降低轮轨间的接触应力峰值。
中端优化前、后的轮轨接触分布如图7和图8所示。结果表明:该方法有效降低了优化过程中轮轨的横向跳跃,优化后轮轨接触分布比优化前更均匀,尤其在尖轨处。
假定轮重为20 t,材料泊松比为0.3,动摩擦因数为0.29,静摩擦因数0.3,杨氏弹性模量为210 GPa,结合CONTACT数值程序[7],得到轮轨在静态接触横移量不同时的正应力和轮对接触斑面积图,如图7~10所示。由图7~10可见:优化后的正应力变小,接触斑面积增加,接触应力峰值减小,从而有效减缓钢轨磨耗,可提高其使用寿命。

图5 中端廓形优化
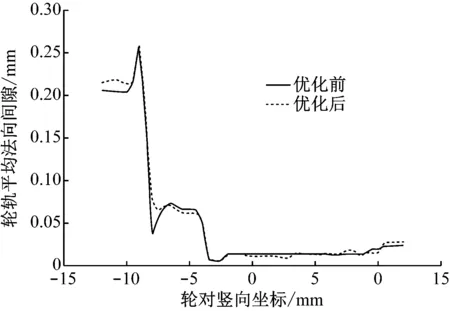
图6 中端轮轨平均法向间隙
转辙区前端和后端的计算结果同转辙区中端计算结果类似。运用改进的轮轨间隙法对廓形优化后,轮轨平均间隙值下降,轮轨间的接触应力峰值降低。接触点位置分布更加均匀,正应力曲线降低,接触斑面积增大,钢轨和车轮之间的相互磨耗减少。

注:图中数字为轮对横移量;灰线表示不同的轮对横移量与轮轨接触点的对应关系
图7 中端优化前左边轮对接触分布
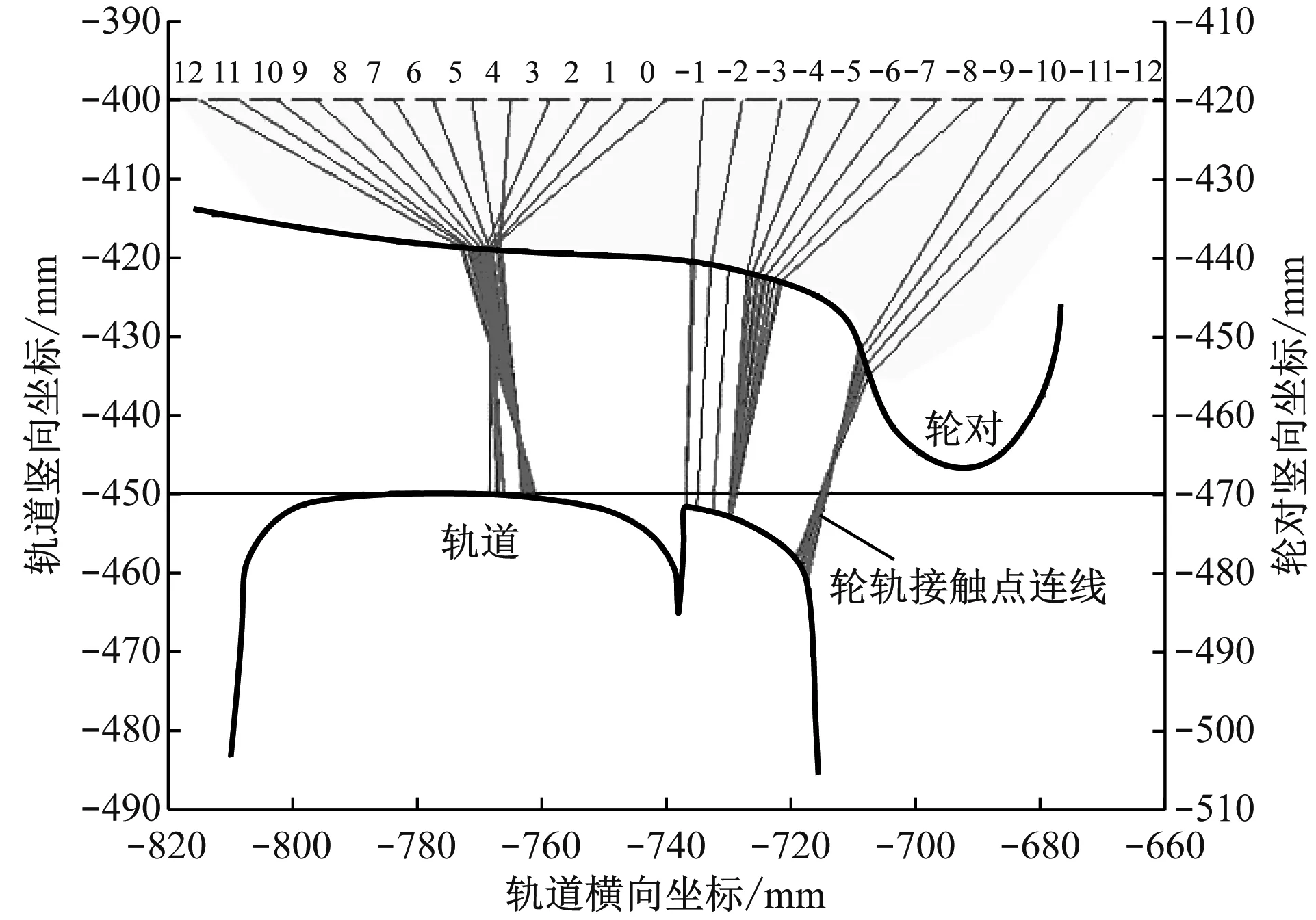
注:图中数字为轮对横移量;灰线表示不同的轮对横移量与轮轨接触点的对应关系
图8 中端优化后左边轮对接触分布
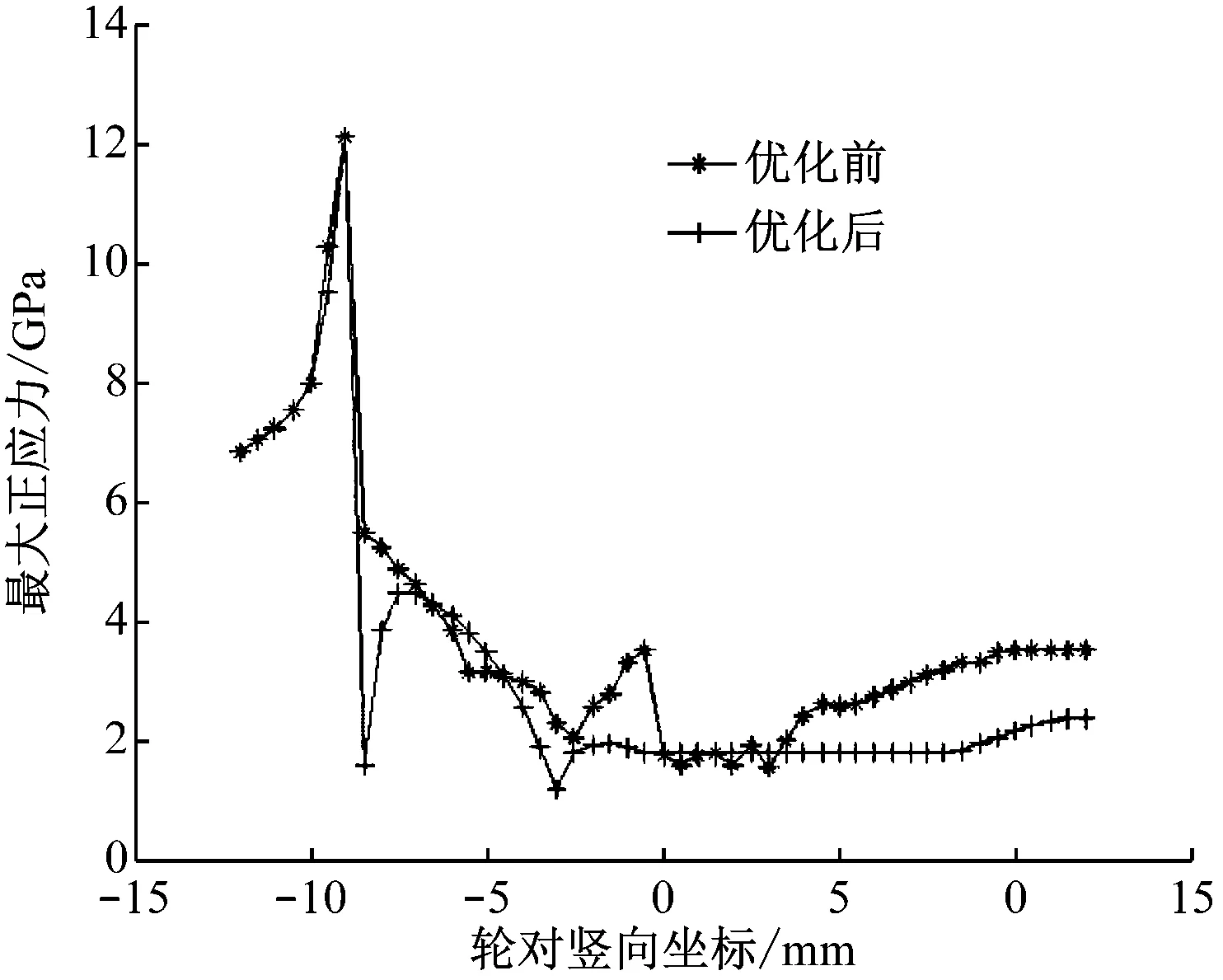
图9 中端最大正应力
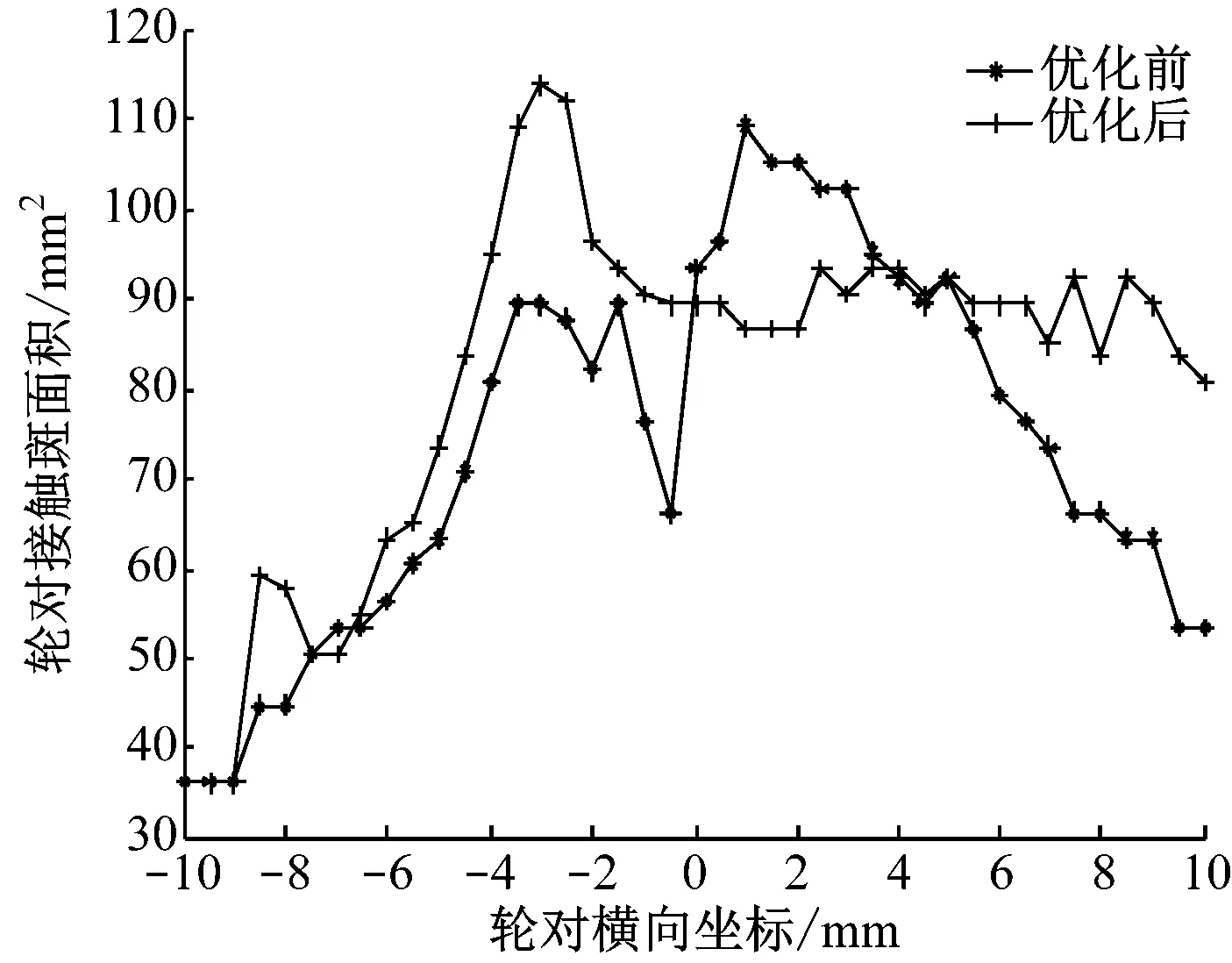
图10 中端接触斑面积
3 结语
借助最小面法向间隙法,在一定改进的基础上优化了道岔区钢轨形面,获得了其目标形面。本文讨论了基本轨和尖轨部分廓形优化,并引入踏面跳跃点横向间距作为优化控制条件,得出以下结论:
(1) 该方法可有效降低轮轨间的平均法向间隙值,增加轮轨的接触面积,降低接触应力峰值。
(2) 该方法使得轮轨接触点在轮对横移范围内分布更加均匀,并且分布范围更加广,可以尽量减少在不同横移量下,钢轨上接触位置重叠的情况。
(3) 该方法对整个横移范围内的接触面积和接触应力值都有所改善,从而能够降低钢轨磨耗,提高其使用寿命,为道岔转辙区打磨提供一个模版。
