基于有限状态机的轨道交通车辆防滑控制建模仿真与验证*
2019-02-15朱文良秦凌光吴萌岭
刁 锋 朱文良 秦凌光 吴萌岭
(同济大学铁道与城市轨道交通研究院,201804,上海//第一作者,硕士研究生)
轮轨黏着制动是目前轨道交通车辆主要的制动方式。黏着制动存在的最大缺陷就是黏着力有限。列车制动时,如制动力大于黏着极限,则轮轨间将产生滑移。轮轨间适当的滑移可以提高黏着利用率,提高制动性能;但若防滑控制不当,则易导致轮对抱死滑行,引起轨面擦伤、制动距离增加、制动耗风量增大、车辆稳定性和舒适性降低等结果,严重影响列车运行安全[1]。因而为提高列车运行的安全性和经济性,减少出现车轮抱死和擦轮的情况,列车防滑器被广泛应用于各类轨道交通车辆中。可以说,防滑控制装置的性能直接影响到制动部件甚至整个列车的安全,必须经过充分的试验和性能检验。但由于实车线路试验成本高、效率低,可重复性低,难以模拟极限条件等,故有必要对其进行仿真与研究[2]。
高速列车制动防滑控制系统主要由制动控制单元(BCU)、气制动单元、防滑阀、基础制动装置等组成。BCU根据制动指令、车体质量及速度计算出所需要的气制动力和目标BC压力(增压缸空气压力)。制动指令进入气制动单元,经防滑阀输出给基础制动装置,使轮对产生减速度。列车制动过程框架如图1所示。
1 制动力学相关模型
1.1 轮轨黏着模型
轮轨黏着模型可用于模拟真实线路黏着条件,包括干轨、湿轨、轨面污染导致的黏着系数突降等工况。需考虑黏着系数同速度及轴重之间的相互关系,以及前后轮间由滑行引起的相互作用关系。车轮和钢轨实际上都是有弹性的。在载荷的作用下,轮轨接触的地方会发生弹性变形,其轮轨接触面呈椭圆状。而轮轨会在接触面间发生微量滑动(即“蠕滑”)[3]。蠕滑的程度可用滑移率s表示:

图1 列车制动过程框架图
(1)
式中:
ω——车轮旋转速度;
r——车轮半径;
v——车体平移速度。
基于Polach黏着理论,黏着力F可表示为:
(2)
其中:
(3)
f=f0[(1-A)e-Bw+A]
(4)
式中:
a——轮轨椭圆接触区纵半轴长度;
b——轮轨椭圆接触区横半轴长度;
C——轮轨接触剪切刚度;
Q——轴重;
f——轮轨摩擦因数;
ε——剪切变形梯度;
A——轮轨间极限滑动速度下摩擦系数与最大摩擦因数的比值;
μ——黏着系数;
f0——轮轨最大摩擦系数;
B——摩擦系数调节参数;
w——滑移速度,即轮轨间的速度差。
根据黏着系数定义:
(5)
将f、F和ε代入可得:
(6)
1.2 车辆动力学模型
车辆模型用于模拟制动过程中的实际位移、速度、减速度、各轴轴速、闸瓦摩擦系数变化、坡道、运行阻力等信息,在MATLAB软件的simulink模型搭建中,根据需要对模型进行简化。一方面,制动过程中不关注车体垂向、横向舒适度指标,且暂不考虑曲线通过,列车制动工况各性能指标主要与纵向自由度有关,且列车纵向自由度同横向及垂向自由度的耦合度较小,故只考虑其纵向自由度;另一方面,若完全考虑车辆各部件的所有自由度(包括垂向、伸缩、点头、横向、侧滚、摇头),则模型极复杂,仿真结果难以收敛,计算量过大[4-5]。图2即简化后的单节车动力学模型拓扑图,自上而下依次包括车体、二系悬挂、构架、一系悬挂、轮对及轮轨黏着力。

图2 单节车动力学模型拓扑图
2 防滑控制气路模型与控制策略模型
2.1 防滑控制气路模型
根据制动系统气路实际参数,建立EP阀、紧急阀、中继阀、防滑阀、制动缸等部件模型,模拟制动过程中气动单元动作,反映制动过程中气路的空气流量、压力升降速度、压力变化过程,以及防滑阀动作频率、次数等信息。利用AMESim软件中的气动元件组成气动模型,其仿真模型结构如图3所示。EP阀根据压力控制信号将预控压力输入中继阀,由中继阀进行流量放大后经防滑阀进入基础制动装置。B11调压阀与紧急电磁阀为中继阀提供紧急制动工况下的预控压力[6-7]。将实车试验数据及阀类试验台试验数据对比,并修正模型,对整个气制动系统模型进行常用阶段制动、缓解和紧急制动仿真。模型对制动指令相应速度快,对制动缸压力模拟准确[8-9]。

图3 气路仿真模型示意图
2.2 防滑控制策略模型
制动控制单元是空气制动系统的核心,其接受制动指令并采集列车上与制动有关的信号,对指令与信号进行计算,得出列车所需的制动力;再向电制动和空气制动系统发出制动信号,同时通过运算协调电制动和空气制动的制动量。此外,该控制单元还会按照程序对各输入信号进行判断、计算,输出控制指令完成控制、安全监测及处理。其中,滑行判断和输出防滑阀的动作信号可实现防滑控制。
目前,在进行防滑控制时,防滑控制系统使用的判断依据主要有速度差、减速度、减速度微分和滑移率。其中,速度差和减速度最常用。
本文以CRH2型动车组的制动系统为研究对象,建立有限状态机模型,来研究空气制动的防滑控制策略。有限状态机模型是一种在实时系统设计中常用的数学模型,以描述控制特性为主,可应用在从系统分析到设计的所有阶段,利用Matlab软件中的Stateflow功能来实现有限状态机模型[10]。滑行再黏着状态机模型示意如图4。

注:A点为判定产生滑行点;B点为开始保压点;C点为确认黏着再恢复点;β为轴减速度;Δv为轴速与参考车速的速度差
图4 滑行再黏着状态机模型示意图
由图4,当某轮对的运动状态符合A点所对应的条件时,制动控制单元判定该轮对即将产生滑行,然后防滑阀按照一定的排风策略对该轮对的制动缸压力进行调节。当该轮对的减速度满足B点的判断条件时,说明此时该轮对的滑行趋势已得到有效的控制,则制动控制单元控制防滑阀将对制动缸进行保压。当速度差值满足C点的判断条件时,制动控制单元认为该轮对的黏着已经恢复,不再产生滑行,故将重新对制动缸进行充气,以恢复制动再黏着。在制动缸压力阶梯式降低过程中,防滑阀保压时间t2=150 ms,防滑阀的缓解时间为:
t1=60×m
式中:
t1——防滑阀缓解时间,ms;
m——倍数,取决于防滑阀的缓解次数n。
n与m关系见表1。

表1 n与m的关系
由表1可知,当列车防滑控制系统检测到轮对产生滑行时,排风阀(RV)第1次排风,n=1,m=1,t1=60 ms。若排风阀排风关闭后。检测到车轮仍在滑行,则排风阀在150 ms后进行第2次排风,排风时间60 ms(n=2,m=1)。如第2次排风后车轮依然滑行,则在150 ms后进行第3次排风,排风时间为180 ms(n=3,m=3)。如果第4次排风300 ms(n=4,m=5)后车轮仍在滑行,则第5次排气6 s(n=5,m=100)排风结束,直至检测到滑行轴的指标处于B状态后开始保压[11-13]。
3 结果验证和分析
基于轨道交通车辆动力学模型、轮轨黏着力模型、制动系统气路模型,以及包含基于Stateflow的防滑控制器制动控制单元模型,通过Matlab软件simulink组件与AMESim软件联合仿真,对干轨(即黏着条件较好,不发生滑行)和湿轨(即低黏着条件,防滑器发生动作)两种工况对整体模型及环境进行验证分析,从而确认仿真模型的有效性。
3.1 干轨工况验证结果
在干轨工况下,仿真计算不同列车初速度下制动距离,并与根据目标减速度计算所得的制动距离进行对比进行验证。分别设置制动初速度为200 km/h、250 km/h和300 km/h,制动级位为紧急制动,目标减速度为[14]:
制动距离的仿真结果和根据目标减速度计算的理论制动距离对比见表2,其误差满足EN 15595中对制动距离模拟的相关要求。

表2 干轨条件下制动距离仿真结果与理论计算值比较
3.2 湿轨工况验证结果
根据EN 15595:2011-07《Rail applications-Braking-Wheel Slide Protection》相关要求,通过调整车辆及轮轨模型参数,完成基于半实物仿真平台的防滑控制试验工况再现。参照标准中相关要求,将仿真得到的制动距离、速度曲线及速度差分布与现有实车试验数据进行对比。半实物仿真试验中,制动初速度为103 km/h,制动级位为紧急制动,模拟轨面喷洒防冻液低黏着轨面条件。
3.2.1 制动距离
EN 15595要求防滑模拟装置制动距离模拟值与真实值误差应小于5%。列车制动距离实车试验值与仿真值对比结果见图5。列车制动距离试验值为748 m,制动距离仿真值为733 m,误差约为2%,满足EN 15595对制动距离模拟的相关要求。

图5 制动距离试验值与仿真值对比
3.2.2 速度曲线
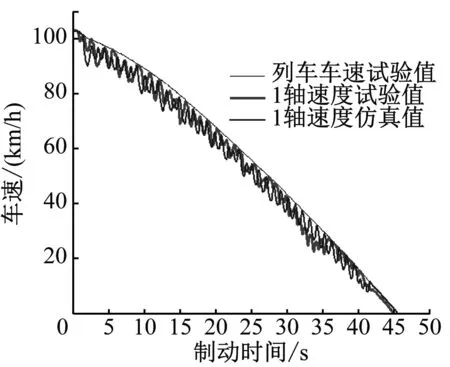
EN 15595对防滑模拟装置对速度模拟的要求为:从开始制动到车速到达15 km/h止任意时刻,试验车速与模拟车速的差值应小于3 km/h,列车车速试验值与仿真值对比结果见图6。同一时刻仿真车速与试验车速最大差值为1.06 km/h,符合EN 15595有关要求。

图6 车速试验值与仿真值对比
3.2.3 滑行工况下各轴速度差分布
以第i轴轮轨间滑移速度Δvi(即轮轨速度差)的均值E(Δvi)和标准差σ(Δvi)作为统计指标,故有:
(7)
式中:
vc——列车速度;
ωi——第i轴的车轮角速度;
t2——制动时间。
在制动初速度为103 km/h、制动级位为紧急制动、模拟轨面喷洒防冻液低黏着轨面条件的仿真工况下,各轴速仿真结果与试验结果对比见图7。
图8为1轴的HV(保压阀)控制信号和RV(排气阀)信号情况,直接反映了滑行过程中防滑阀组的动作情况。

表3 各轴速度差仿真值与试验值统计对比
a) 1轴

b) 2轴

c) 3轴

d) 4轴
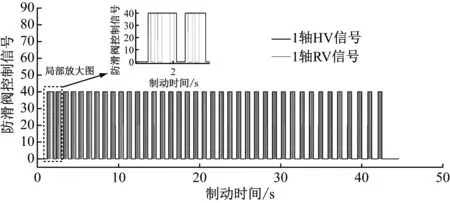
图8 1轴保压阀和排气阀动作信号
4 结语
针对轨道交通车辆制动系统的防滑控制研究,可通过Matlab及AMESim等软件建立仿真模型,并进行计算机仿真。
实际线路对极限工况的模拟难度大,可重复性低。本文搭建的有限状态机模型能有效模拟滑行进程,为防滑控制器的设计提供支持。
通过对不同黏着条件的仿真验证,以及同实车数据的对比,确认了整个仿真模型的有效性。
基于有限状态机理论的防滑控制器在滑行工况下作出的响应和判断满足要求,将有限状态机模型应用在防滑控制器仿真设计上是合理的。
