基于寿命周期费用的系统可靠性与维修性关系研究*

潘洪亮 徐 曌,2 唐少强

(1. 同济大学国家磁浮交通工程技术研究中心， 201804， 上海；2. 同济大学道路与交通工程教育部重点实验室， 201804， 上海//第一作者，副研究员)

系统的可靠性和维修直接影响系统的可用性和寿命周期费用。因此，需以可用性为目标进行可靠性与维修性的综合权衡，并获取最优寿命周期费用效能，使系统在稳定运行前提下拥有最低的系统寿命周期费用。

1 可靠性与维修性的权衡分析

可靠性与维修性的权衡分析以可用性为目标。假设系统具有稳定可靠性R(t)，是单一总成或严格串联的[1]。系统在t= 0时以可使用状态开始工作，在t时刻仍处于可使用状态(即刻可以工作)的有效度为A(t)，则由更新方程(renewal equation)，有:

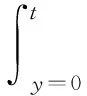
(1)

式中:

R(t)——系统可靠度,以至t时刻为止无故障的概率表示；

n(t)——系统的更新率(renewal rate)，即当系统进行一系列运转-故障-修理-再运转循环时，其进入“运转”状态的比率。

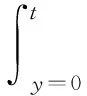
(2)

式中：

h(t)——失效前时间与修复时间之和的联合概率密度函数。

若用g(t)表示失效前时间(即“工作”时间)的概率密度函数，用f(t)表示修复时间(即“停机”时间)的概率密度函数, 则通过g(t)与f(t)的卷积可得到h(t):

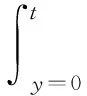
(3)

假设其系统有

g(t)=λexp(-λt)

(4)

f(t)=μexp(-μt)

(5)

式中:

λ——故障率；

μ——修复率。

对式(1)～(5)取拉普拉斯变换，得：

A(s)=R(s)+R(s)n(s)

(6)

n(s)=h(s)+h(s)n(s)

(7)

h(s)=g(s)f(s)

(8)

把式(8)代入式(7)，得：

n(s)=g(s)f(s)/[1-g(s)f(s)]

(9)

再将式(9)代入式(6)，并用概率密度函数g(s)来表达R(s)，有：

R(s)=[1-g(s)]/s

(10)

故式(6)可转变为：

A(s)=[1-g(s)]/{s[1-f(s)g(s)]}

(11)

因为密度函数g(t)与f(t)的拉普拉斯变换是：

(12)

把式(12)代入式(11)，并变换为时间定义域，得：

A(t)=μ/(λ+μ)+

[λ/(λ+μ)]exp[-(λ+μ)t]

(13)

也可用平均故障间隔时间(tMTBF)和平均维修时间(tMTTR)来表示：

(14)

由式(14)可见，当t增加时，式(14)右边的第二项逐渐减小，有效度趋近其极限成为常数，即

(15)

通过式(15)即可进行磁浮列车悬浮系统的维修性与可靠性的综合权衡分析。

依据长沙磁浮列车现场状况，假设悬浮系统tMTBF最小值为400 h，tMTTR最大值为6 h。A依次取0.970,0.980,0.990,0.995,0.999，计算tMTBF与tMTTR的关系，并指出当tMTBF>400 h，tMTTR<6 h时，符合要求的tMTBF与tMTTR的综合权衡范围(见图1)。

图1 可靠性与维修性权衡分析范围

2 系统寿命周期费用计算模型的建立

寿命周期费用(CLC)是系统在预期的寿命周期内，为其论证、研制、生产、使用与保障以及退役处理所支付的所有费用之和[2]。CLC涉及经济，技术，管理多方面学科的理论研究，可覆盖系统从决策论证、设计、生产试验、使用、后期维护直至报废处理的整个寿命周期产生的费用，也可针对系统寿命周期的某阶段费用进行分析研究。通过CLC的分解、预测和评价，可实现对CLC的优化和方案的取舍[3]。可见，CLC是一个极其重要的经济性量化指标，为系统的设计、选择、使用及报废提供了决策依据[4]。

系统都是以实现一定的功能为目的。影响到系统实际功能的各种因素，就是影响系统CLC的因素。系统的实际功能由其技术性能及可用性决定。因此，影响系统技术性能及可用性的因素也就是影响系统CLC的因素。图2为CLC的影响因素。

在系统寿命周期分析的基础上，可以建立费用计算模型如下：

CLC=C0+Cos+Cdr+Cf

(16)

式中：

C0——原始投资费用，包括调研、研制及生产制造等费用；

Cos——运行费用，包括能耗、人工等费用；

Cdr——退役处理费；

Cf——维修保障费用。

Cos与Cdr为常数，可由经验得到。C0与Cf由可靠性和维修性决定。

图2 CLC影响因素

2.1 原始投资费用C0

系统的造价C0与R的关系可以归结为系统中各单元的造价与可靠度之间的函数关系。系统中单元i的造价Ci与可靠度Ri关系难以建立，其原因为：① 缺乏足够的统计数据；② 对任何单元都有效的函数关系式是不可能存在的，单元材料、型式有多种选择和组合，而Ci与Ri都同材料、型式有关，故当单元采用不同材料和型式时其Ci与Ri的关系也不会相同；③ 影响Ci与Ri关系的因素很多，除材料和型式外，还有加工质量、环境、生产力发展水平和人力物力资源等。因此,严格说来,Ci与Ri的关系不是一一对应的[5]。

为此，定义Ci与Ri的关系为：Ri达到某一值所需的最小造价，或在Ci一定时把该费用充分用于提高其可靠度所达到的最大Ri。

有关Ci与Ri关系的公开发表文献很少见到。文献[6]指出，CiRi具有下列基本性质：1个低可靠度单元的成本较低，1个高可靠度单元的成本很高；C1对Ri的导数是1个单调递增函数。根据经验有：

(17)

式中：

ai——待定经验参数，无量纲量；

bi——R趋于0时的系统造价。

ai决定曲线的趋势，ai值愈小，C(R) 曲线前段的坡度愈平，而后段愈陡。

对于磁浮交通系统，适用于指数分布。将Ri=1-λ=1-1/tMTBF代入式(17)得：

C0=Σ(ailn (tMTBF)+bi)

(18)

C0与tMTBF的函数关系如图3所示。

图3 C0与tMTBF关系图

2.2 维修保障费用Cf

Cf一般占CLC的60%以上，尤为重要。而保障费用是Cf的主要费用来源。由文献[7]，有

Cf=CaLt/tMTBF

(19)

式中：

Lt——系统寿命周期；

Ca——每次故障平均费用。而且

Ca=Cs(tMTTR+tr)+CrtMTTR+Crp

(20)

式中：

tMTTR——平均维修时间；

Cs——单位时间停机损失;

tr——维修等待时间;

Cr——单位时间维修费用;

Crp——维修零件费用。

将式(20)代入式(19)，有

(21)

结合式(16)可得:

CLC=Cos+Cdr+Σ(ailn (tMTBF)+bi)+

(22)

为权衡tMTBF和tMTTR的取值，考虑到Cos、Cdr、bi为常数，对取值没有影响，因此对C0+Cf取最小即可得最小CLCo且

C0+Cf=Σailn (tMTBF)+

(23)

CLC与tMTBF的关系如图4所示。

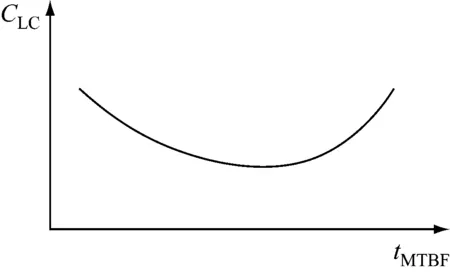
图4 CLC与tMTBF的关系

3 算例分析

根据系统CLC计算模型，结合可用度进行可靠性与维修性权衡分析，以中低速磁浮列车悬浮系统为例对其CLC进行计算。

中低速磁浮列车依靠列车下部悬浮架上安装的悬浮电磁铁通电后与轨道F形磁极面之间产生的电磁吸力，从而实现悬浮。中低速磁浮列车的悬浮系统极为重要，关系到磁浮列车的正常运行[8]。

根据现场情况，整理3组中低速磁浮列车悬浮系统相关数据如表1所示。

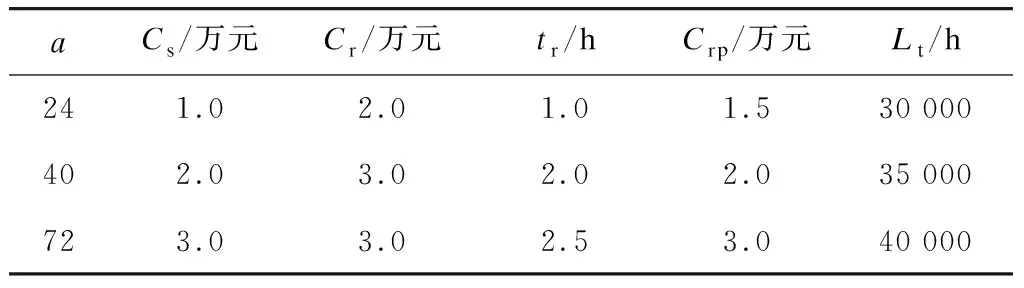
表1 磁浮列车悬浮系统数据

中低速磁浮列车悬浮系统有效度目标为A=0.999，tMTBF≥400 h，tMTTR≤6 h。根据式(1)～(15)得到约束条件：

(24)

取CLC最小值为：

CLC,min=Cos+Cdr+Σ(ailn (tMTBF)+bi)+

(25)

通过Matlab软件得到tMTBF与CLC的仿真计算结果如图5～6所示。

图5 tMTBF与CLC关系仿真结果图

图6 仿真结果求导处理图

通过图5可以看出CLC与tMTBF的函数关系，并对tMTBF求导得到图6，证明CLC存在最小值。3组数据计算结果如下：

第一组：当tMTBF=3 125 h，tMTTR=3.13 h时,CLC,min=352.13万元。

第二组：当tMTBF=5 250 h，tMTTR=5.26 h时,CLC,min=597.64万元。

第三组：当tMTBF=5 833 h，tMTTR=5.84 h时,CLC,min=871.33万元。

在悬浮系统设计阶段，以0.999的有效度为目标，每组悬浮系统的数据都可得到tMTBF及tMTTR，以在保证系统稳定性的同时达到最小的CLC。

由计算结果可以看出，先通过有效度进行维修性与可靠性的综合权衡，再通过寿命周期费用模型进行计算，可得到最小CLC对应的维修性与可靠度关系，为系统设计提供数据支持。

4 结语

通过以可用性为目标的可靠性与维修性权衡分析，可使得系统的CLC达到最低。首先，根据可用性对系统的可靠性和维修性之间进行综合平衡，以确保串联系统在其整个运行期间足够稳定；然后，对维修性及可靠性进行量化处理，建立系统寿命周期费用计算模型，计算出合理的可靠性与维修性，并使得系统的CLC最小；最后，以长沙中低速磁浮列车悬浮系统为例，利用Matlab软件建立模型，进行仿真计算，从而获得最佳方案。