一种基于全站扫描的特征点自约束点云变形分析方法
2019-02-15,,,,
,, ,,
(1. 信息工程大学,河南 郑州 450001; 2. 上海航天设备制造总厂有限公司,上海 200245)
变形监测在保障国家生产发展、国民生命财产安全方面有着非常重要的意义,常用的变形监测数据采集技术包括全站仪测量技术、GPS技术、三维激光扫描技术等。全站仪测量技术最早应用于变形监测,目前技术成熟、应用广泛[1-4]。通过全站仪获取特征点高精度三维坐标用于变形分析,能够对变化明显的点位进行高精度观测。经过多年发展,全站仪逐步具备了自动目标识别(ATR)、目标锁定跟踪等功能,能够进行无人值守自动化变形监测,具有效率高、人力成本低等优势。但全站仪只能进行单点测量,监测点数少,不能反映变形体的整体形变情况,信息量较少。GPS技术与全站仪技术一样能精确测量单个点的变形量,但监测点数少,难以对变形体的整体变形进行精细监测,而且一旦被破坏会严重影响资料的连续性[5-7]。三维激光扫描技术数据获取的速度更快,数据量大,方法更简便,受到的外部因素影响更少,因此在应用于变形监测时具有常规测量手段所不具有的优势:数据量大、能够获取形变体细部信息、数据获取操作简便易行等。但在实际应用中还存在一些问题亟待解决:相对于全站仪测量技术和GPS测量技术,扫描点位精度较低;变形分析的方法还不成熟,需要完善,同时建模效果不理想也会影响变形分析;没有统一的精度评定标准等[8-16]。
全站扫描仪可以进行传统的全站仪测量和三维扫描测量,不仅能获取高精度的单点坐标,还能获取目标的点云数据,并且集成了其他多项先进的测量技术,是近年来的一项重要技术革新[17]。全站扫描仪扫描频率较低,远不及普通扫描仪百万赫兹级别的点云获取效率,但它拥有更高的扫描精度,由于其具有全站仪测量模式,能够进行设站,在点云数据拼接方面更高效,精度更高,从而具有广泛的应用空间。
综上所述,现有的变形监测技术主要基于某种单一传感器进行数据处理和分析,无法全面反映变形体的整体变形信息。本文提出基于离散特征点和点云数据的综合变形分析方法,并通过试验验证该方法的可行性和可靠性。
1 基于离散特征点和点云的综合变形分析模型
1.1 总体框架
基于全站扫描的特征点自约束点云变形分析模型,利用离散特征点多期点位数据求取形变矢量,并对扫描点云数据进行预处理和三维模型重建,根据特征点分布分割形变控制区域,最后求取变形后扫描点云相对于前一期三维模型的形变参数,实现对变形体的综合变形分析,全面反映变形体的形变规律。具体技术路线如图1所示,主要技术难点包括变形体三维模型重建、形变控制区域分割、点云至模型形变分析。
1.2 数据获取与处理
模型中涉及的数据包括特征点的点位数据和变形体的整体点云数据。特征点点位数据可以通过全站仪、GNSS测量获得。其中,全站仪测量包括精密测量和免棱镜测量两种方式,棱镜测量精度高、自动化程度高;免棱镜模式精度稍低,但操作方便,无需架设棱镜,一般在变形体无法架设棱镜时使用[18]。在实际应用中,根据精度需要采取不同方法。变形体的整体点云数据主要通过三维激光扫描获取。对变形体进行多期观测,每一期观测均采集特征点坐标和整体点云数据。
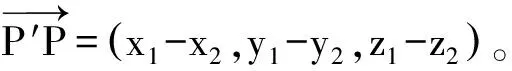
初始获取的点云数据由于边缘效应、扫描区域过大等因素存在较多冗余点,需通过去噪等预处理进行剔除。预处理后对第1期点云进行三维建模,模型精度会对本文的分析方法精度产生一定影响,需要选择合适的重建方式,确保三维模型具有较高精度,能够较为真实地反映变形体的实际形态。本文采用Wrap算法[19]重建变形体三维模型,该算法能够针对具有复杂拓扑结构的曲面构筑精细三角网进行重建,具有良好的重建效果和较高的重建精度。
1.3 特征点控制区域分割
在变形监测中,特征点一般分布在变形体可能产生显著形变的区域,能够反映这一区域的形变趋势,具有一定代表性。变形体较大时,布设的特征点相应较多,对于相距较远的两个特征点而言,两者形变趋势及大小可能会有较大差别,因此需要对变形体整体点云数据进行分割,确定每个特征点的控制区域。
本文采用最近特征点搜索算法对特征点控制区域进行分割。如图2(a)所示,A表示变形体点云中的一点,P1、P2、P3为布设的不同特征点,Uj(j=1,2,3)为第j个特征点控制区域,依次计算A到Pj的距离dj,d1=min{dj}为最短距离,因此A∈U1,由特征点P1对A进行形变控制。同理,通过遍历,确定各特征点控制区域内点云,从而实现特征点控制区域的分割。
通常情况下,上述方法能够对大部分变形体点云数据进行分割,但若变形体出现塌陷、断层等剧烈变形时,会造成形变控制区域分割错误,最终得到错误的形变分析结果。如图2(b)所示,变形体出现塌陷分为塌陷区域S1和未塌陷区域S2,A点属于塌陷区域S1点云中一点,即A∈S1,A到P1的距离d1小于A到P2的距离d2,若将A划分为P1所属控制区域,利用P1点形变信息作为参照分析A处形变,则会出现错误结果。
为解决上述问题,需对出现塌陷等形变的变形体进行剧烈形变探测,即探测剧烈形变处的分界点。首先对点云数据法向量和曲率几何特征进行估算,设ai为三维点云中任意点,可以利用K-nearest算法[20]求得点ai的k个近邻点集,M(ai)={aij|1≤j≤k},利用这些点拟合最小二乘平面,满足下式
(1)
式中,ni为该平面的法向量。该问题等价于对点ai邻域的协方差矩阵进行主元分析,ai邻域的协方差矩阵可以写成
(2)
(3)
求得点云法向量及曲率后,计算每一个点的不一致性指标。设ai及其近邻点aj的法向量为nai和naj,θij为nai和naj之间的夹角,则ai的不一致性指标就是与其邻近点集的法向量夹角的均方根值,即
(4)
对所有点的不一致性进行统计分析,设定阈值筛选出可能的分界点,再利用区域生长算法[21]进一步对候选分界点进行筛选,最终确定准确的剧烈形变处的分界点。
在进行最近特征点搜索之前,判断特征点及点云是否位于分界点同侧,图2(b)中,P1∈S2,P2∈S1,P3∈S1,P2、P3、A属于同侧,均位于塌陷区域S1,只需判断A至P2、P3的距离大小,从而确定A由哪个特征点控制。
1.4 点云至模型形变分析
为了计算点云到模型的形变量,反映变形体细部的形变信息,本文提出了基于离散特征点约束的点云形变量分析模型。其基本思想为:对变形体第1期三维点云进行模型重建,利用特征点两期观测获得的形变矢量控制第2期扫描点云的形变方向,计算点云按此方向至三维模型的偏移量,即为点云至三维模型的形变量。模型的算法步骤为:
(1) 获取特征点的形变大小及方向,计算特征点形变矢量。特征点的形变矢量本身能够在一定程度上衡量变形体的变形规律,在本文中又作为控制点云形变方向的基准,是后续分析变形体点云形变量的基础数据。
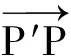
(3) 计算形变量。直接利用空间两点间距离公式计算出点云中点与模型中对应点的距离,即为所求形变量。图3点云中点A′的坐标为A′(x′,y′,z′),模型上的对应点A的坐标为A(x,y,z),则在A′处点云至模型的形变量为
(5)
对变形体进行两期扫描,其扫描范围不尽相同,特别是位于边缘的点云,在搜索模型上对应点时,可能与模型没有交点,无法计算此处形变量。因此在获取点云数据时,应尽量使第1期点云完全覆盖变形体,可适当向外延伸。
1.5 模型精度评价
基于全站扫描特征点自约束点云变形分析模型的核心思想为:利用变形体变形后的点云数据与前一期点云数据重建的三维模型进行比对,得出变形体的整体形变参数,过程中借助特征点的形变参数作为控制基准。影响点云相对模型形变量精度的因素主要包括扫描点云数据点位误差Δ点、三维模型重建误差Δ模、形变方向误差Δ方等,这些误差相互独立,则变形体形变误差为
Δ=Δ点+Δ模+Δ方
(6)
中误差计算式为
(7)
式中,扫描点云点位中误差m点和形变方向中误差m方可以通过计算公式估算获得。目前对三维模型重建精度的评定研究较少,缺乏统一评定标准,无法为重建模型提供较为准确的精度估计值,因此无法直接利用上式评价综合变形分析模型精度[22]。本文提出采用直接比较法验证模型精度,分析模型在变形监测中应用的可行性,基本思想为:通过更高精度的测量手段获取变形体的形变量D基,即空间位移,作为评价系统的形变真值,同时利用本文提出的变形分析方法获取点云中所有点至三维模型的形变量D1,D2,…,Dn,n表示点云数量,求取形变量真误差为
Δi=Di-D基i=1,2,…,n
(8)
对真误差进行统计分析,计算真误差期望值,判断其是否无偏,是否存在明显的系统误差。利用真误差计算形变中误差为
(9)
形变中误差m即可作为评价模型精度的重要依据。
2 试验与分析
2.1 试验准备
本文利用Leica MS60全站扫描仪获取变形体数据,MS60同时具有全站仪测量功能和三维点云扫描功能,且其测距测角与扫描同轴,所获取的精密单点坐标与扫描点云坐标属于同一个坐标系,无需进行坐标转换。MS60主要技术参数见表1。

表1 MS60测量技术参数
采用高分子复合材料制作了800 mm×800 mm的小型沙盘,强度高,质量适中。将沙盘通过转接装置固定于精密对点仪上,精密对点仪能够精确整平,可以在水平方向上沿两个互相垂直的方向移动,移动距离通过千分尺测量获得,精度达到1 μm,远高于全站扫描仪测量精度。在沙盘上布设4个反射片,作为特征点P1、P2、P3、P4。试验所需主要设备如图4所示。
2.2 试验方法
选定适当位置放置精密对点仪并固定,精确整平,将沙盘水平固定于其上再次精密整平。架设全站扫描仪,测量获取沙盘上特征点坐标,并对沙盘进行三维扫描,获取点云数据。将精密对点仪分别向水平面内两个互相垂直的方向移动10 mm,其精度由千分尺精密控制,而沙盘实际在空间中平移了14.1 mm。移动后,再次测量特征点坐标,并扫描获取沙盘移动后点云数据,作为变形观测第2期数据。按照本文提出的变形分析方法对两期数据进行分析并验证模型精度。
2.3 试验结果与分析
按照上述试验方法采集了沙盘的两期变形观测数据,包括特征点坐标及整体点云数据。两期特征点点位坐标见表2。

表2 特征点两期点位坐标 m
将两期点云数据进行去噪等预处理,剔除冗余点,并对第1期沙盘点云数据进行模型重建,得到结果如图5所示。图5(a)点云孔洞区域为特征点所在处,由于反射片回光反射较强,全站扫描仪扫描时无法获取反射片处点云信息,重建模型后对孔洞进行了修复(如图5(b)所示)。
利用本文提出的综合形变分析方法计算点云中所有点沿离散特征点形变方向至三维模型的形变量,并由式(8)计算形变真误差,求出真误差的期望Ε(Δi)=-0.04 mm,接近于0,表明本方法计算的形变量具有无偏性,未出现明显的系统误差,效果良好。由式(9)计算形变中误差为m=±1.2 mm,且最大误差值均控制在2倍中误差以内。试验结果表明,通过利用离散特征点信息和变形体三维模型,使具有不可重复性的点云在模型中找到虚拟点对,进一步计算出点云的偏移量,能够从整体和细节上反映出变形体的形变信息,并具有较高精度。
3 结 语
本文分析了现有监测方法的优点与不足,结合全站扫描仪在数据获取方面的优势,提出了基于全站扫描特征点自约束点云变形分析方法,阐述了特征点区域分割、点云至模型形变分析等关键环节,并提出采用直接比较的方法验证模型的精度;设计了变形模拟试验,验证了本文提出方法的可行性和可靠性。试验结果表明,利用本文提出的方法能够获取变形体整体形变信息,其真误差期望为-0.04 mm,形变中误差为±1.2 mm,同时也包含特征点形变信息,能够较为全面真实地反映变形体的形变规律。
