补偿弯臂长度对Z形补偿管段应力的影响

马懿明， 唐汝宁， 高明亮

(1.北京首钢国际工程技术有限公司，北京100043；2.内蒙古工业大学,内蒙古呼和浩特010051；3.内蒙古建筑勘察设计研究院有限责任公司，内蒙古呼和浩特010011)

1 概述

在实际工程中，受施工场地的限制，通常在满足疲劳分析的强度条件下，尽可能地缩短Z形补偿管段补偿弯臂长度(一般取1.25～2.00倍弹性臂长)，但笔者研究发现，此时Z形补偿管段弯头出现的最大范式等效应力并不一定为最小值。范式等效应力(Von-Mises Stress)属于一种屈服准则，本文简称为等效应力。等效应力是一个综合的概念，可以用于对疲劳、破坏等的评价，是弹塑性力学中的一个力学概念，遵循材料力学第四强度理论(形状改变比能理论)。可表示模型内部的应力分布情况，从而使分析人员快速地确定模型中最危险区域。

此外，Z形补偿管段的理论计算是通过弹性抗弯铰解析法将Z形补偿管段中的一个弯头单独隔离出来进行简化的疲劳分析得出弯头应力变化幅度。通过对比发现，运用弹性抗弯铰解析法求解得出的Z形补偿管段弯头应力变化幅度随补偿弯臂长度增加而产生的变化趋势，与有限元分析法所得出的变化趋势并不一致。若将Z形补偿管段推广到组合弯头，则组合弯头无法通过弹性抗弯铰解析法得出准确的应力变化幅度，需通过有限元分析法进行确定。本文采用有限元模拟方法，对水平埋设Z形补偿管段等效应力进行模拟，分析Z形补偿管段最大等效应力出现最小值时补偿弯臂长度。

2 有限元分析

2.1 研究对象

Z形补偿管段的平面布置见图1，被补偿弯臂1、2均取水平转角直管段在循环温差作用下的过渡段长度，补偿弯臂分别取1～14倍弹性臂长。设定条件：保温管工作管钢材选取Q235B，直管工作管规格为D1220×14，直管保温管外护管外直径为1.39 m。计算安装温度为10 ℃，工作循环最高温度120 ℃。弯头曲率半径为2.5倍的直管工作管公称直径(1 200 mm)，角度90°，弯头壁厚为14 mm。设计压力为1.6 MPa。

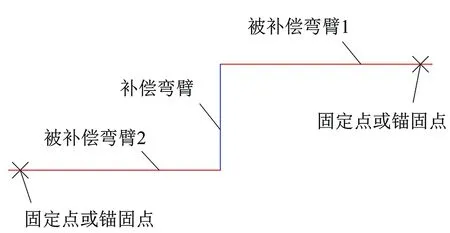
图1 Z形补偿管段的平面布置

弹性臂长Le的计算式为[1]：

(1)

(2)

(3)

式中Le——弹性臂长，m

k——与土壤特性和保温管刚度有关的参数，m-1

Dc——直管保温管外护管外直径，m

C——土壤横向压缩反力系数，N/m3，本文取4×106N/m3

E——钢材的弹性模量，MPa，本文取19.8×104MPa

Ip——直管工作管横截面的惯性矩，m4

ro——直管工作管外半径，m

ri——直管工作管内半径，m

将已知参数代入式(1)～(3)，可计算得到弹性臂长Le为13.45 m，向上圆整为14 m。

水平转角直管段在循环温差作用下的过渡段长度Lt的计算式为[2]：

(4)

式中Lt——水平转角直管段在循环温差作用下的过渡段长度，m

Z——计算系数

Fb——弯头两侧臂长相等时的轴向力，N

Fmin——单位长度最小摩擦力(按管中心线位于地下水位以上考虑)，N/m

式(4)中计算系数Z的计算式为：

(5)

(6)

(7)

(8)

(9)

(10)

式中A——工作管弯头管壁横截面面积，m2

φ——转角管段的折角(邻补角)，rad

Cm——计算系数

K——弯头工作管柔性系数

Rc——弯头的计算曲率半径，m，为3 m

Ib——弯头钢管的横截面惯性矩，m4

λ——弯头的尺寸系数

δb——弯头的壁厚，m

rbm——弯头横截面的平均半径，m

rbo——弯头的外半径，m

rbi——弯头的内半径，m

弯头两侧臂长相等时的轴向力Fb的计算式为：

Fb=106As[αE(t1-t0)-νσt]

(11)

(12)

式中As——工作管直管管壁横截面面积,m2

α——钢材的线胀系数，K-1，本文取12.4×10-6K-1

t1——管道工作循环最高温度，℃，本文取120 ℃

t0——管道计算安装温度，℃，本文取10 ℃

ν——钢材的泊松数，取0.3

σt——环向应力,MPa

p——设计压力，MPa

Di——直管工作管内直径，m

δ——直管工作管壁厚，m

单位长度最小摩擦力Fmin的计算式为：

(13)

σv=ρgh

(14)

式中μmin——保温管外护管与土壤间的最小摩擦系数，取0.2

K0——土壤静压力系数，取0.5

σv——管道中心线处土壤应力，Pa

G——包括介质在内的保温管单位长度自重，N/m，本文取15 818 N/m

ρ——土壤密度，kg/m3，本文取1 800 kg/m3

g——重力加速度，m/s2，取9.8 m/s2

h——管中心线覆土深度，m，本文取2.197 m

将已知数据代入式(4)～(14)，可计算得到水平转角直管段在循环温差作用下的过渡段长度Lt为235 m。根据CJJ/T 81—2013《城镇供热直埋热水管道技术规程》第5.7.2条的相关规定，计算过渡段热伸长量。经校核，循环温差大于工作管屈服温差。基于校核结果，可计算得到被补偿弯臂1、2的热伸长量均为262.5 mm。

2.2 模型建立

采用Ansys软件(15.0版本)的静力结构模块的Solid186单元建立Z形补偿管段模型(见图2，图2为补偿弯臂长度为1倍弹性臂长的情况)。Solid186单元是一个高阶3维20节点固体结构单元，具有二次位移模式。Solid186单元通过20个节点来定义模型，每个节点有3个沿着x、y、z方向平移的自由度，具有任意的空间各向异性，支持塑性、超弹性、蠕变、应力刚化、大变形和大应变能力。

受计算机硬件条件限制，图2中Z形补偿段的被补偿弯臂1、2均取1倍弹性臂长，但被补偿弯臂1、2的热伸长量仍赋予262.5 mm。被补偿弯臂1的热伸长方向为Ox的负方向，被补偿弯臂2的热伸长方向为Ox的正方向。

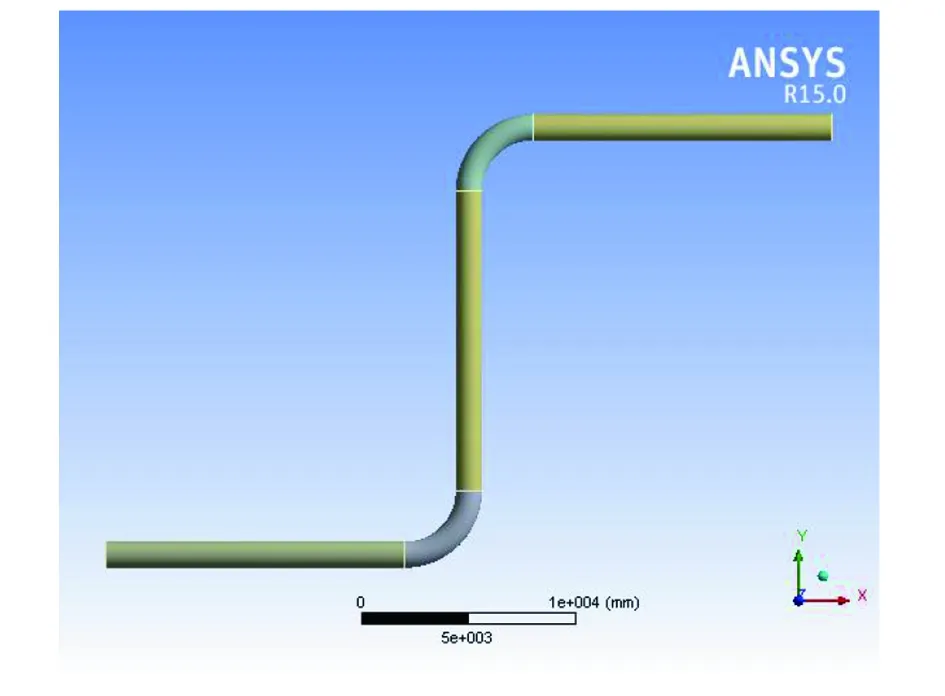
图2 Z形补偿段模型

2.3 荷载施加

① 内压

通过Ansys软件中以下命令将内压(设计压力1.6 MPa)施加在管道内表面：Static Structural-Loads-Pressure-Geometry Selection-Face。具体如下：选中模型-施加荷载-选择荷载类型-定义为压力-选中模型内表面，完成内压的施加。

② 静土压

取管顶埋深为1.502 m，通过Ansys软件中以下命令将静土压施加在管道外表面：Static Structural-loads-Pressure-Geometry Selection-Face。具体如下：选中模型-施加荷载-选择荷载类型-定义为压力-选中模型外表面，完成静土压的施加。静土压的计算方法按CJJ/T 81—2013的第5.6.3条执行，计算结果为38.75 kPa。

③ 温度荷载

通过Ansys软件中以下命令将温度荷载(在管道计算安装温度基础上附加管道工作循环最高温度)施加在管道上：Static Structural-loads-Thermal Condition-Geometry Selection-Body。具体如下：选中模型-施加荷载-选择荷载类型-定义为温度-选中模型本体，完成温度荷载的施加。

④ 位移荷载

通过Ansys软件中以下命令施加：Static Structural-Supports-Displacement-Geometry Selection-Face。具体如下：选中模型-施加荷载-选择荷载类型-定义为位移-选中弯臂端面-输入位移量，完成位移荷载的施加。

⑤ 土壤压缩反力

由于土壤压缩反力的作用，弯头变形能力将受到限制，因此在弯头与土壤接触面施加弹性支撑(即土弹簧)。通过Ansys软件中以下命令施加：Static Structural-support-Elastic support-Geometry Selection-face。具体如下：选中模型-施加约束-选择荷载类型-定义为弹性支撑-选中模型弯头与土壤接触面，完成弹性支撑的施加。借鉴工程中通常在弯头两侧布置泡沫垫(厚度取60 mm)的施工方法，并考虑保温管保温层的吸收变形能力及土壤压缩反力作用，根据文献[3]表5.1，选取综合基床系数为3 251 kN/m2。

2.4 网格划分

采用Multi Zone(多区域)网格划分方法。多区域划分网格的特征是自动分解几何，从而将一个体分解成可扫掠体，以扫掠方法得到六面体网格，适用于由若干个规则几何组成的体。鉴于弯头形状比直管复杂，弯头处网格划分较为光滑。网格划分后的Z形补偿段(局部)见图3。

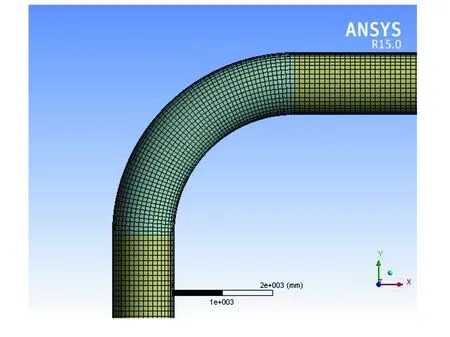
图3 网格划分后的Z形补偿段(局部)

2.5 结果后处理

① 应力水平

在模拟结果中查看Von-Mises Stress(范式等效应力)，当补偿弯臂长度为1倍弹性臂长时的等效应力分布见图4(以被补偿弯臂2对应的弯头为例)。由图4可知，弯头外壁面红色区域出现了最大等效应力，为420.28 MPa。

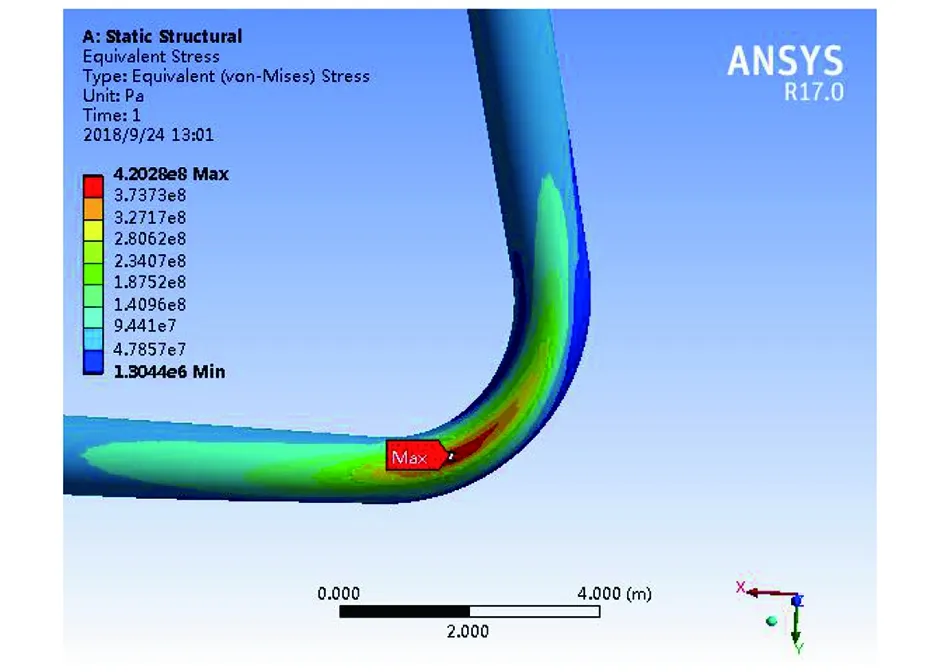
图4 当补偿弯臂长度为1倍弹性臂长时的等效应力分布

② 数据分析

将Z形补偿管段的被补偿弯臂保持循环温差作用下的过渡段长度不变，采用上述方法对补偿弯臂分别取2～14倍弹性臂长的Z形补偿管段等效应力进行模拟。由模拟结果可知，补偿弯臂取2～14倍弹性臂长的Z形补偿管段最大等效应力均出现在图4所示位置，最大等效应力见表1。

表1 不同补偿弯臂长度对应的最大等效应力

由表1可知，Z形补偿管段最大等效应力随着补偿弯臂长度的增大先减小后增大。补偿弯臂长度由1倍弹性臂长增加到4倍弹性臂长时，最大等效应力迅速减小。补偿弯臂长度为4～9倍弹性臂长时，最大等效应力随补偿弯臂长度的增大而减小，但变化幅度不大。当补偿弯臂长度大于9倍弹性臂长后，最大等效应力随着补偿弯臂长度的增大逐渐增大。最大等效应力的最小值出现在补偿弯臂长度为9倍弹性臂长时。由模拟结果可知，当补偿弯臂长度小于1.5倍弹性臂长时，弯头的最大等效应力大于3倍钢材许用应力(钢材许用应力取125 MPa)，此时弯头应力较大，易发生疲劳破坏。

3 结论

针对工作管(材质为Q235B)规格为D1220×14的保温管，在被补偿弯臂取循环温差作用下的过渡段长度，补偿弯臂分别取1～14倍弹性臂长的条件下，对水平埋设Z形补偿管段的最大等效应力(范式等效应力，基于第四强度理论)进行有限元模拟，分析Z形补偿管段最大等效应力出现最小值时对应的补偿弯臂长度。

Z形补偿管段最大等效应力(出现在弯头外壁)随着补偿弯臂长度的增大先减小后增大。补偿弯臂长度由1倍弹性臂长增加到4倍弹性臂长时，最大等效应力迅速减小。补偿弯臂长度为4～9倍弹性臂长时，最大等效应力随补偿弯臂长度的增大而减小，但变化幅度不大。当补偿弯臂长度大于9倍弹性臂长后，最大等效应力随着补偿弯臂长度的增大逐渐增大。最大等效应力的最小值出现在补偿弯臂长度为9倍弹性臂长时。由模拟结果可知，当补偿弯臂长度小于1.5倍弹性臂长时，弯头的最大等效应力大于3倍钢材许用应力(钢材许用应力取125 MPa)，此时弯头应力较大，易发生疲劳破坏。