雷达探测能力评估模型研究

(火箭军工程大学， 陕西西安 710025)

0 引言

雷达探测能力如何是衡量评估雷达技战术性能的一项重要指标，其主要取决于雷达系统参数、目标特性及环境因素。目前，大多数文献对雷达探测能力的评估是依托于雷达方程、Blake图表法或是雷达威力覆盖图[1-5]，这也是目前较为通行的做法。虽然这些评估方法都是以具体的距离值作为量化指标来衡量雷达的探测能力，但也存在两点不足。其一，雷达接收机噪声和目标横截面的统计特征决定了雷达作用距离是一个以概率而不是简单的数字来描述的概念[1]，因此，距离指标必须附上雷达探测一个特定距离上规定目标的概率。其二，传统的雷达探测评估方法对雷达系统损耗的估计比较繁琐，其损耗估计只包括了可预测可估计的部分，而对于那些无法预测和不可估计的损耗类别(如人员操作损耗)采取忽略不计，这将导致雷达探测评估结果的不准确。

实际上，无论对何种体制的雷达而言，其首要目的是成功检测到目标，因为目标检测概率的高低是保证雷达及雷达网其他处理环节正常实施的关键影响因素[6]。因此，考虑建立一种基于目标特性为Swerling模型的雷达探测能力评估方法，该评估方法通过Swerling模型，建立起发现概率与最大探测距离之间的数学关系，实现以特定距离上目标对应的发现概率为指标来衡量评估雷达的探测能力。同时，该评估方法还引入了修正因子M，可用这个M因子对最大探测距离进行修正得到实际距离。最后，通过已建立的评估模型和M因子，以发现概率为指标对一个敌雷达网的威胁程度进行了仿真和评估。

1 探测能力评估模型建立1.1 雷达方程的形式

雷达方程能够将雷达最大探测距离与发射机、接收机、天线、目标特性及工作环境关联起来。因此，根据关键雷达参数和平均目标截面积可得雷达最大探测距离Rmax，其表达式[1]为

(1)

式中，

(2)

式中：Pt为峰值发射功率；Gt为发射天线增益；k=1.38×10-23为玻耳兹曼常数；T0为有效噪声温度，通常取290 K；Ae为天线有效接收面积；Bn为雷达接收机带宽；Fn为系统噪声系数；(SNR)min为最小可检测信噪比，单位为自然数字。K称为“威力系数”，当雷达工作体制和雷达参数确定了以后，K就可视为常数。

事实上，式(1)的雷达方程形式并不能恰当地预测雷达在工作中的实际距离。因为该雷达方程中并没有引入比较繁杂的雷达系统损耗的影响因素。即便如此，式(1)仍是雷达探测评估的重要工具，Rmax也是探测评估中关注的重要参数。如果考虑了雷达系统损耗L和方向图传播因子F的影响因素，则式(1)可扩展成更准确的形式[7]：

(3)

式中：

(4)

SNR为信噪比，单位为自然数字；R为实际探测距离；M为修正因子；其余参数定义同式(1)。尽管雷达方程有很多不同的形式，但式(3)可被视为最广泛、要素最全面的雷达方程形式[7]。文献[1]指出，经常发现实际探测距离R只有最大探测距离Rmax的一半。如果在不改变式(4)中参数M和SNR的前提下，由此推算，式(3)中威力系数K须为原来16倍。

1.2 目标起伏模型

关于目标起伏模型，不少文献都有相关描述。最早的是对非起伏目标模型的介绍，Marcum最早提出的是非起伏目标模型，并给出了该情况下的发现概率与信噪比关系的数学关系[7]。但非起伏目标在实际中并不常遇到。在实际情况中，大多数目标与雷达之间是存在着相对运动关系，导致了目标截面积也会随雷达视线角的变化而发生起伏[8]。大多数起伏目标的统计特性由卡方分布表述。现有模型中，目标统计特性服从卡方分布且在理论上比较成熟的有4个常用的Swerling模型[7-10]。该模型对于一些导弹飞机等目标的拟合性很好，常被用于分析雷达对目标的检测性能。关于不同Swerling模型下，n个脉冲积累时发现概率与信噪比的关系表达式[7]为

Pd=Swerling_N(Pfa,n,(SNR)dB)

(5)

式中：Pd为发现概率；Pfa为虚警概率；n为非相干积累脉冲数；(SNR)dB为信噪比，单位dB；Swerling_N代表不同Swerling模型的函数关系。

这样，通过式(1)、式(5)的关系，既可以建立起在给定的虚警和发现概率下，雷达所能够达到的最大探测距离，即

Rmax=f(Pfa,n,Pd)

(6)

式中，f为构建Rmax与概率的某种函数关系。式(6)的关系就相当于以概率而非简单数字形式完整地描述了雷达探测距离。

1.3 雷达发现概率与实际探测距离关系

由式(6)可知，雷达最大探测距离与虚警、发现概率成函数关系。如果在获知了某雷达的虚警和发现概率时的最大探测距离Rm，就可由式(6)确定威力系数K，且可代入到式(1)为

(7)

同样地，在保持K不变时，在实际探测距离R时的信噪比为

(8)

式中：(SNR)R为实际探测距离时信噪比，M为此时对应的修正因子。

由式(8)/式(7)后取对数为

(SNR)R-dB=

(SNR)Rm-dB+40lg(Rm/R)+10lg(M)=

(SNR)Rm-dB+40lg(Rm/R)+[M]dB

(9)

式中,以dB为下标均表示该参数取对数后以dB为单位的形式。将式(9)代到式(5)的函数关系中作为输入量就可以建立起发现概率与实际探测距离R之间的数学关系。即

Pd=Swerling_N(Pfa,n,(SNR)R-dB)

(10)

这样就得到式(10)的探测能力评估模型，可以用来解决多脉冲积累时的雷达实际探测距离评估问题。

2 修正因子M的计算

在上面的模型建立中，为了得到实际探测距离而引入了修正因子M来定量描述雷达系统损耗等因素对雷达探测能力评估的综合影响。所以，修正因子的计算就成了预测雷达实际探测距离很关键的一点，本节将提出一种基于目标特性的修正因子M的计算方法。

2.1 Albersheim方程及其对应的雷达方程

多脉冲积累方式可极大地改善雷达的检测能力。对于非起伏目标而言，当积累n个脉冲时单脉冲所需信噪比的近似值可由Albersheim的经验公式得到，其表达式[1]为

lg(A+0.12AB+1.7B)

(11)

函数表达形式如下：

(SNR)n-dB=Albersheim(Pfa,n,Pd)

(12)

式中：(SNR)n-dB为n个脉冲积累时所需的单个脉冲信噪比，以dB为单位；A=ln(0.62/Pfa)和B=ln[Pd/(1-Pd)]。该方程在n=1～8 096，Pd=0.1～0.9，Pfa=10-3～10-7范围内的误差小于0.2 dB。该方程只适用于线性检波而非平方律检波。且上面得到的信噪比可代入到式(1)雷达方程形式为[1]

(13)

式中的参数定义同前面。

2.2 Shnidman方程及其对应的雷达方程

Albersheim方程为非起伏目标(SNR)n-dB提供了一种简单的近似计算，而对于起伏目标情况，Shnidman提出的解决Swerling型目标信噪比(SNR)n-dB的经验近似[11]。其方程表达式为

(14)

(15)

(16)

(17)

C1={[(17.700 6Pd-18.449 6)Pd+

14.533 9]·Pd-3.525}/K

(18)

(19)

(20)

(21)

结合式(6)可写成函数表达式如下：

(SNR)n-dB=Shnidman(Pfa,n,Pd)

(22)

Shnidman方程的精度相比于Albersheim方程要差一些。文献[11]指出，对于0.1≤Pd≤0.99，10-9≤Pfa≤10-3且1≤n≤100，(SNR)n-dB的估计误差小于0.5 dB。同时，发现概率Pd范围比Albersheim方程要宽得多，n的范围要小很多，但已经满足实际系统的需要，该方程只适用于平方律检波。

同样地，也可以将上面得到的信噪比代入到以下雷达方程形式[1]：

(23)

式中的参数定义同前面。与式(13)相比，式(23)的雷达方程多了一个起伏损耗Lf，这也是起伏和非起伏目标的不同之处。

2.3 M因子的计算方法

总结来说，Albersheim方程或Shnidman方程提供了基于Swerling型目标特性下，非相干积累n个脉冲所需的单脉冲信噪比的计算方法，其具体判断流程图如图1所示。

图1 信噪比(SNR)n的计算求解流程

根据奈曼-皮尔逊准则，在满足规定虚警概率Pfa和发现概率Pd时的检测性能所要求的是最小信噪比[1]，也就是说，式(13)、式(23)的雷达方程形式对应的距离是最大探测距离。而在雷达实际的应用中，需要知道的是实际距离，由式(3)可知，如果考虑了雷达损耗而又要保留式(13)或式(23)中的其他参数，这时有

(24)

式中：Ls为雷达系统除起伏损耗Lf外其他一切损耗的总和；此时的修正因子M=F/LfLs，其余参数的定义同前面。

由式(24)、式(13)或式(23)可以推导得到：

[M]dB=[F/Ls]dB-[Lf]dB=-12.04-[Lf]dB

(25)

式中：以dB为下标均表示该参数取对数后以dB为单位的形式。式(25)不管对起伏还是非起伏目标都是适用的，如果是非起伏目标的话，[Lf]dB=0。这就是说明，对于非起伏目标情况下，其实际探测距离预测为最大探测距离的一半是合理的，但对起伏目标而言，预测实际距离时则必须考虑到起伏损耗的影响。因为起伏损耗Lf是一个与Pd、Pfa和Swerling模型有关的函数[7]，所以，上面的M因子可写成函数形式如下：

[M]dB=M_factor(Pfa,Pd,n,sw_case)

(26)

式中,sw_case为Swerling目标类型。如此，就可以形成先通过Shnidman或Albersheim方程得到最大探测距离Rmax，然后再用对应的修正因子M修正即可得到实际探测距离R。M因子与发现概率的关系如图2所示。

图2 Swerling I模型下M因子与发现概率的关系

3 实际应用

3.1 雷达对抗态势构建

对任何体制雷达而言，虚警概率Pfa、发现概率Pd与信噪比之间存在稳定关系不会因雷达而异[12]。所以，以上所建立的模型和M因子算法也不会因雷达而异。根据文献[6]的信息，对于某一特定雷达的Rmax一般是指Pfa=10-6、Pd=0.5时，雷达对截面积为1 m2目标的最大探测距离。根据这样的信息和脉冲数就可以确定雷达的威力系数K，从而对雷达探测能力展开更深入的评估。

构建一雷达对抗态势，以敌雷达网对我方目标形成威胁为假想背景，对抗场景如图3所示。

图3 雷达对抗场景假设

在实际情况中，己方对敌雷达网信息掌握会很有限的，一般能够获知的也就是各成员雷达的最大探测距离等有限信息，具体如表1所示。

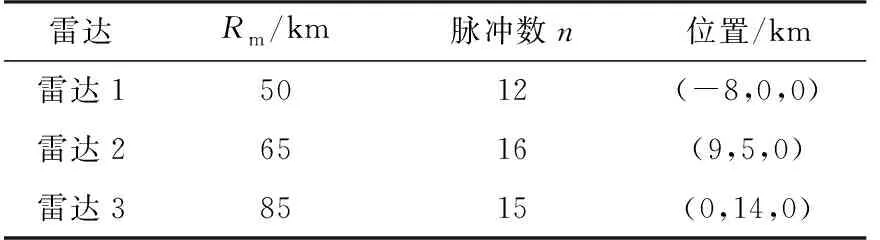
表1 雷达网中各成员雷达的信息

而己方飞机的信息如表2所示。

表2 飞机飞行参数

根据表1、表2的信息可以算出飞机分别与雷达1，2，3随时间而变的实际距离为

(27)

3.2 已知条件可确定的各成员雷达参量

根据表1、表2信息和建立的模型，可根据以下步骤确定各雷达的一些可知参量。

第一步：根据飞机这类的目标特性，判断目标特性符合Swerling I模型;

第二步：根据图1判断流程可知，信噪比计算工具为Shnidman方程；

第三步：根据概率Pfa=10-6、Pd=0.5时对应雷达最大探测距离，即可通过Shnidman方程算出各雷达初始化参量K和(SNR)Rm-dB;

第四步：将算出的初始化参量代入到式(9)得到各雷达信噪比与实际距离关系，再将信噪比代入到式(5)可建立起发现概率与实际距离的关系。

根据以上的数据处理过程，可以得到各雷达的初始化参量具体值如表3所示。

表3 各雷达的初始化参量

由表3中的威力系数K可以看出各雷达之间性能优劣对比，K越大，雷达性能越好。由于雷达网的性能是各成员雷达性能的综合体现，所以，从一定程度讲，各成员雷达性能优劣也决定着一个雷达网的性能优劣。

3.3 雷达网的仿真评估

通过上面两节的雷达信息和数据处理，可以进一步对雷达网进行评估。为了对敌雷达网的威胁程度作一个保守估计，引入了文献[6，13]中秩1准则的雷达网评估模型如下：

Pd=1-(1-Pd1)(1-Pd2)(1-Pd3)

(28)

式中：Pd1，Pd2，Pd3分别为各雷达对目标的发现概率，Pd为雷达网对目标的发现概率。通过对式(10)的探测能力评估模型可以得到雷达网仿真曲线如图4所示。

图4 雷达网评估曲线

通过图4可以看出，雷达网对目标的威胁程度要大于单部雷达对目标的威胁程度，说明各雷达经过组网后的效果更好。假如雷达网的Pd≥ 0.990就可认为达到火控雷达的告警要求，那么根据曲线可得一个关于距离域的范围为：Rmax≤50.92 km，经过M因子修正来换算成各雷达与目标的实际距离满足：

(29)

由式(27)、式(29)的约束条件可得到，敌雷达网对目标的告警时间段为：t=42.72～49.12 s。也就是说，在飞机抵近雷达网的过程中，到42.72 s时雷达网开始达到火控雷达告警时刻，随着飞机继续飞行，就会逐渐远离雷达网，直到49.12 s后雷达网失去飞机的火力精确打击机会，整个对飞机有威胁的时间持续了6.4 s。这个以时间为指标的评估结果可为飞机的干扰策略提供指导，从而保证飞机安全。

4 结束语

建立了一个基于目标特性的雷达探测能力评估模型，实现了将距离以概率的形式进行完整描述。与传统的评估模型不同的是，该模型条件简单、适用范围广，在实际应用中，可用于以发现概率为指标的雷达网的仿真评估，对于雷达评估模型是一次创新。