含负刚度动力吸振的混合隔振系统振动冲击响应特性分析

2019-02-13苏智伟黄修长吴静波华宏星

中国舰船研究 2019年1期

关键词：元件冲击振动

苏智伟，黄修长，2，吴静波，华宏星，2

1上海交通大学机械与动力工程学院，上海200240

2高新船舶与深海开发装备协同创新中心，上海200240

3海军研究院，北京100161

0 引言

为了降低水雷、鱼雷等爆炸引起的冲击载荷对舰载设备带来的影响和破坏，通常会在设备和安装基座之间设置减振抗冲器来隔离振动及提供抗冲击过载保护。从振动的角度看，当隔振系统的固有频率小于0.707倍激励频率时，可以隔离振源；从冲击的角度看，当冲击脉冲的持续时间小于隔振系统固有周期的1/6时，冲击被隔离［1］。目前，舰船上广泛采用的减振抗冲器包括橡胶隔振器、气囊隔振器等，它们均具有很好的工程实用性，也得到了广泛的研究。不仅如此，学者们还在研究多介质、新机理的减振抗冲器，例如非线性新型气液耦合冲击耗能器［2］、Ruzicka隔振器［3］等。

从原理上讲，减振抗冲器若能在冲击发生时具有非常软的刚度、在冲击结束后恢复较高的刚度，则被认为是一种理想的冲击隔离器，这种冲击隔离器具有在冲击发生时响应小、位移能够限位的特点［4］。基于该思路，Ledezma-Ramirez等［5］构建了一种可变刚度的冲击隔离器，从原理性试验角度验证了其能量消耗的机理。Huang等［6］提出了一种高静、低动非线性刚度隔振器，在刚度、质量存在调节误差的情况下对其进行了冲击响应的研究和试验，结果表明，高静、低动非线性刚度隔振器具有优于线性隔振器的隔离冲击能力。

随着舰载设备朝着大型化方向发展，减振抗冲器需要承受大载荷，即意味着大刚度。因此，若要达到高静、低动的目的，通常需要并联负刚度（NS）元件，即负的动刚度元件（kn=dF/dx＜0，其中F和x分别为该元件的力和位移响应），这些元件可以是失稳碟簧、失稳欧拉压杆、连杆弹簧负刚度机构、斜置弹簧负刚度机构、磁性负刚度机构等［7］。但是，在空间有限的情况下，若要获得大的负刚度非常难，实现三向负刚度也较难。

鉴于大载荷隔振器本身的刚度就比较大，若抵消一定比例的正刚度，所需的负刚度也会较大，故在有限的舰用空间内实现大的负刚度难度非常大。为解决传统动力吸振器在低频实现吸振效果所需吸振质量非常大的难题，本文将引入一种含负刚度动力吸振器（DVA）的混合隔振系统。该系统中，负刚度元件所需实现的负刚度较小，且含负刚度动力吸振的减振抗冲器在最优参数下的刚度和阻尼均较高，可以实现无谐振峰的振动传递［8-9］。文献［9］推导了含负刚度动力吸振的混合隔振系统的最优参数，并针对连杆弹簧负刚度机构实现的负刚度混合隔振系统开展了振动响应研究，以分析各种弹簧力、惯性力之间的平衡。但针对该类减振抗冲系统冲击特性的研究较少。

本文将针对含负刚度动力吸振的混合隔振系统研究其振动传递特性和冲击响应特性，建立振动传递特性最优情况下混合隔振系统最优参数的表达式，获得最优参数下的振动传递特性和冲击响应特性，并与传统动力吸振器进行比较分析。

1 理论模型

图1所示为在刚性基础上的含负刚度动力吸振的混合隔振系统动力学模型。该模型在传统有阻尼动力吸振器模型的基础上，在吸振质量和刚性基座之间增加了一个负刚度元件。

图1 含负刚度动力吸振器的混合隔振系统模型Fig.1 Dynamic model of a hybrid isolation system based on DVA with NS

1.1 振动传递动力学模型建模和最优参数

图1所示系统动力学模型的运动方程及表征传递特性的传递力方程如下：

式中：M为被隔振设备；ks为吸振器刚度；m，ke和c分别为传统含阻尼动力吸振器的质量、刚度和阻尼；kn为负刚度元件的负刚度，本文假设kn不随频率和相对位移幅值变化；F为施加在M上的外部激励力；FT为传递到刚性基座的力；，和，分别为M，m位移响应对时间t的二阶及一阶导数。

进行傅里叶变换，获得频率域内的响应X，Y和力传递率（或振动传递率）T分别为：

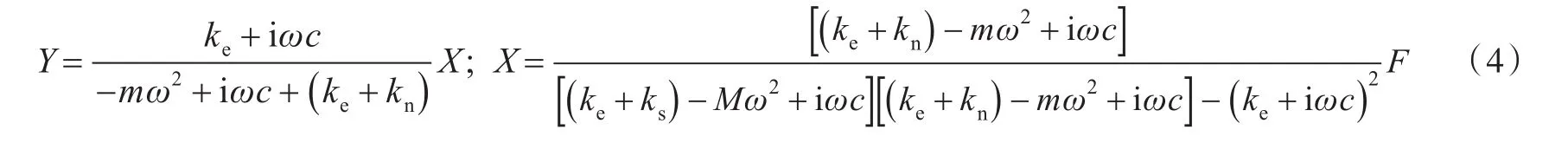
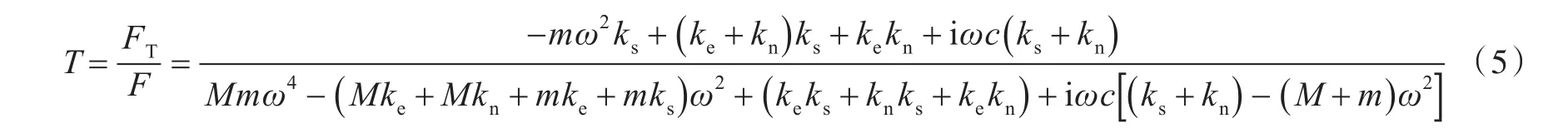
式中：i为虚数单位；ω为外部激励力频率。

根据Routh-Hurwitz判据，可知稳定性条件为：

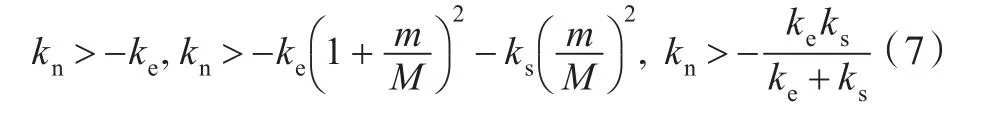
在上述条件下，含负刚度动力吸振的混合隔振系统的固有频率不会出现负值，系统稳定。

分别引入质量比μ、刚度比N、负刚度比p、固有频率ωn、频率比β和阻尼比ξ的无量纲化参数

得到振动传递率T的无量纲表达式为

利用不动点理论，得到不同μ和p情况下最优的传递率Topt、刚度比Nopt和阻尼比ξopt分别为：

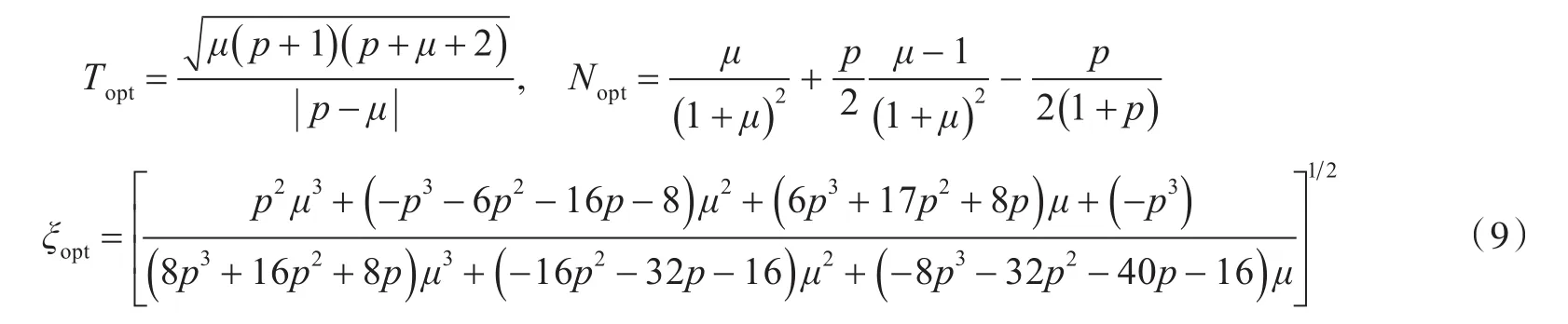
1.2 冲击动力学模型建模

冲击响应动力学模型的运动方程如下：

式中，刚性基础的位移z为半正弦单波冲击的基础位移，，其中 0≤t≤T，Z0为冲击的位移幅值。

假设无量纲时间τ=ωnt，归一化处理后可得到关于τ的响应表达式为：

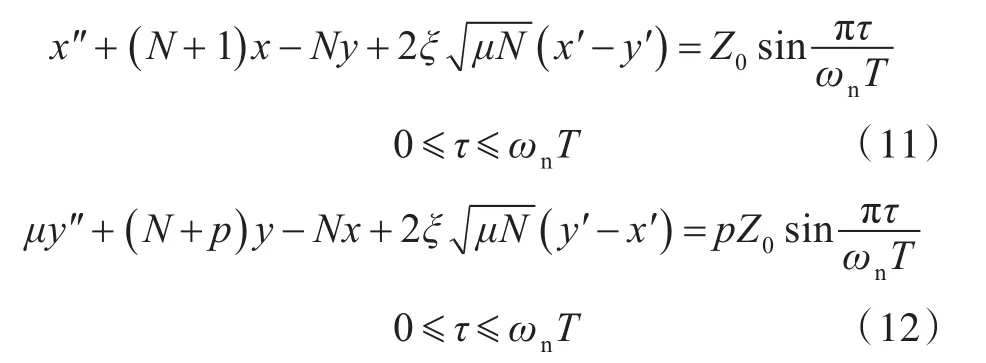
由上式可见，冲击响应与系统的固有频率ωn有关。在以下分析中定义一无量纲输入参数π/ωnT，研究 π/ωnT=1/6，1和6时的冲击响应（对应无量纲的脉宽输入为0≤τ≤6π，0≤τ≤π，0≤τ≤π/6），并假设ωn=1，Z0=1。重点考察被隔振设备和吸振器的冲击加速度、隔振器的相对位移、吸振器刚度元件的相对位移以及负刚度元件的相对位移。式（11）和式（12）采用龙格—库塔法进行求解。

2 数值模拟和讨论

2.1 振动传递特性

以负刚度比p和质量比μ为设计变量，根据式（9），可得最优刚度比Nopt、最优阻尼比ξopt、最优传递率Topt的变化规律如图2所示。可见，因需满足式（7）中的稳定性要求，以及最优阻尼根号内的参数为非负的要求，Nopt，ξopt只有在一定的p，μ组合空间内才有物理意义。在有物理意义的组合空间内，Topt峰值随着p绝对值的增大而减小，与μ的关系复杂。当p绝对值较小时，随着μ的增大先减后增；当p绝对值较大时，随着μ的增大而增大，这意味着μ并不是越大越好，即振动控制效果也取决于p。当μ较小时，p在其绝对值合适时能够以较小的N，ξ优化参数，获得较小的T，这个参数组合具有很大的吸引力。

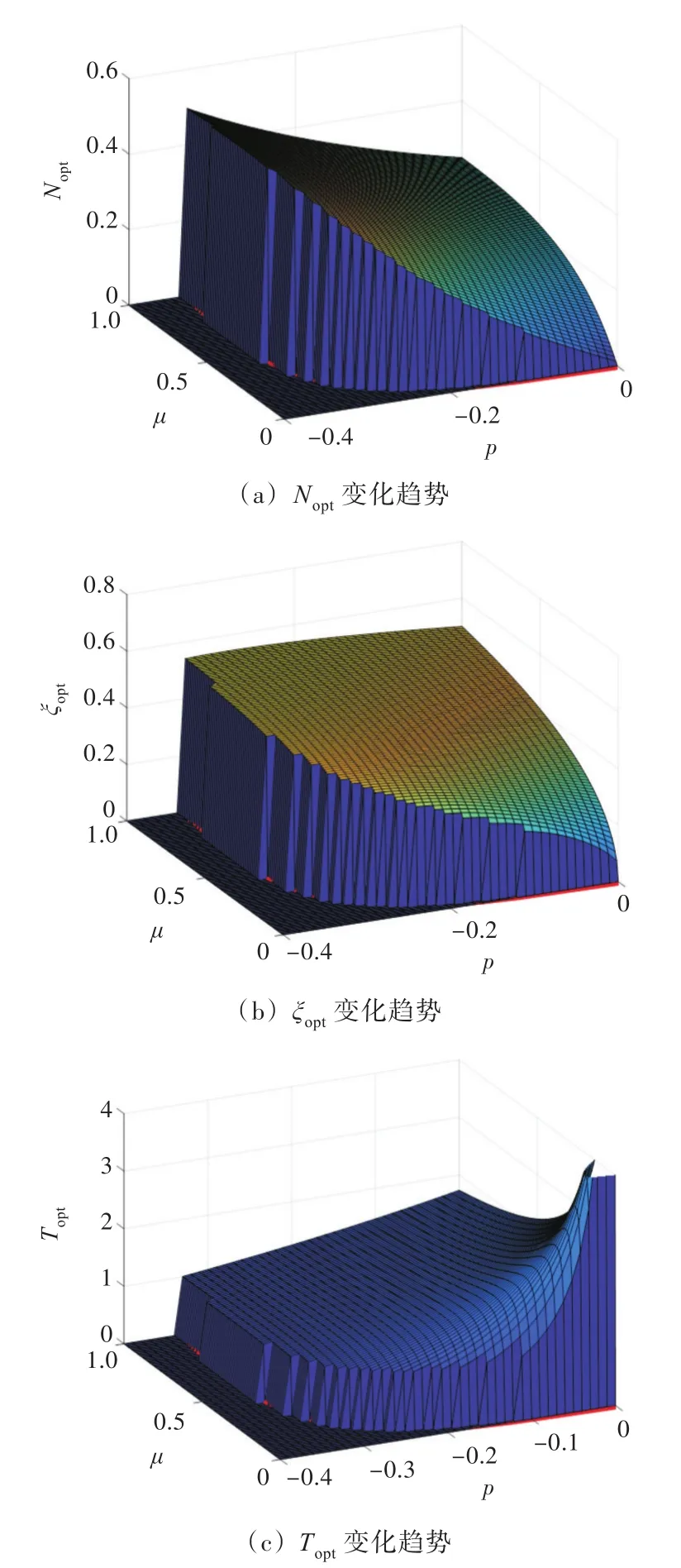
图2 最优刚度比、阻尼比、传递率随负刚度比p和质量比μ变化的趋势Fig.2 The result ofNopt，ξoptandToptas a function of p and μfor rigid foundation

为了分析μ和p对隔振性能的影响，分别给出了2种最优的μ和p情况下含负刚度动力吸振的混合隔振系统振动传递率曲线，如图3所示。同时，给出了传统动力吸振器的振动传递率。在传统动力吸振器中，假设负刚度元件不存在，其他参数与含负刚度动力吸振的参数相同。可见，当μ小时，负刚度动力吸振的效果要优于传统动力吸振，且当p绝对值较大时，会出现无谐振峰的振动传递特征；在μ较大、p绝对值小时，负刚度动力吸振的效果与传统动力吸振的相当；当p绝对值大时，负刚度动力吸振的效果在共振峰处要优于传统动力吸振。从图3的对比可知，在负刚度动力吸振的情况下，吸振子的质量并不一定需要很大，这样可减少传统动力吸振器用于低频控制时对吸振质量的要求。

图3 两组最优参数下传统动力吸振器与混合隔振系统的振动传递率对比Fig.3 Transmissibility comparisons of DVA-based system with NS and traditionalDVA in two groups ofoptimalparameter

图4所示为不同μ和p组合下随着频率变化的振动传递率曲线。由图可见：当p绝对值小时，传递率曲线中的双峰结构特征明显，但随着μ的增大，曲线中峰值处的传递率降低；在p绝对值大的情况下，当μ＞0.15后，传递曲线中峰值处的传递率基本上不再随μ的增加而增加，且在μ小的情况下还出现了无谐振峰的振动传递特征；当μ较小时，在p绝对值小的情况下，曲线中的双峰结构特征明显，随着p绝对值的增大，逐渐变化为无谐振峰的振动传递特性。在μ大的情况下，传递曲线中的峰值随着p绝对值的增加而减小，但不会改变双峰结构特征。

2.2 冲击响应特性

冲击响应特性与输入脉宽相关。为了分析μ，p和脉宽对冲击隔离性能的影响，给出了3种脉宽输入参数（π/ωnT=1/6，1，6）时2种μ及2种p下含负刚度动力吸振器的冲击响应，并将结果与传统动力吸振器进行了对比。由于在μ=0.2时，不同的p（p=0，-0.02，-0.08）下响应基本相同，且3种脉宽输入参数下的冲击响应均得到了很好的控制，故这里不再赘述。

图5～图7所示为μ=0.005时不同的p（p=0，-0.02，-0.08）下计算3种脉宽输入得到的冲击响应结果。3种情况下吸振器的阻尼比参数均采用最优值ξopt（根据式（9）计算得到）。其中，p=0时对应于传统动力吸振器。

图4 两组最优参数下混合隔振系统振动传递率对比Fig.4 Transmissibility comparisons of DVA-based system with NS in two groups of optimal parameter

图6 π/ωnT=1时传统动力吸振器与混合隔振系统的冲击响应对比（μ=0.005）Fig.6 Shock response comparisons of traditional isolation system and DVA-based hybrid system with NS when π/ωnT=1（μ =0.005）

图7 π/ωnT=6时传统动力吸振器与混合隔振系统的冲击响应对比（μ=0.005）Fig.7 Shock response comparisons of traditional isolation system and DVA-based hybrid system with NS when π/ωnT=6（μ =0.005）

从以上图可知：在脉宽输入参数πωnT=1/6时，传统动力吸振器的响应衰减速度较慢，需经过很多个周期才能衰减至0，随着负刚度绝对值的增大，加速度响应和位移响应将越快衰减至0，这是由于最优阻尼比ξopt变大的缘故；在πωnT=1时，传统动力吸振器的响应衰减有限；在πωnT=6时，传统动力吸振器的响应发散，但含负刚度动力吸振的混合隔振系统的响应很快得到衰减，采用含负刚度动力吸振后，吸振器m的位移有所增大，但在3种脉宽输入参数情况下隔振器刚度ks的相对位移均有所减小，被隔振设备M和吸振器m的加速度响应减小。