近场MIMO雷达直线阵列的稀疏优化设计
2019-02-12刘电霆
周 祥,刘电霆
(1.桂林理工大学 a.机械与控制工程学院; b.广西空间信息与测绘重点实验室, 广西 桂林 541006;2.天津大学 微电子学院,天津 300072)
0 引 言
多输入多输出(multiple input multiple output, MIMO)雷达是利用多天线同时发射信号和多天线同时接收目标回波, 获得远多于实际天线数目的观测通道,其性能优于传统体制雷达。 近年来, 采用一维直线阵列(简称为线阵)的MIMO雷达开始用于穿墙探测、 安检等场合,前景十分广阔。由于MIMO雷达天线阵列的构型决定了其成像模式,为降低系统硬件成本和复杂度等,常采用稀疏线阵来减少阵元数目。稀疏线阵的优化设计成为了当前国内外研究的热点[1],其研究主要针对远场应用,一般采用相位中心近似原理(phase center approximation, PCA)[1],即发射和接收分置的天线阵元由其中心位置的一个收/发共用的相位中心等效[2-8],来设计和分析MIMO雷达天线的稀疏直线阵列。
目前,对近场MIMO雷达线阵稀疏优化设计研究不多,且常沿用PCA设计。Zhuge等[9]在满足孔径要求和旁瓣水平约束下,通过在发射和接收孔径函数之间进行相干调节,优化设计线阵,使发射和接收天线阵元的数目最少;陈刚等[10]根据分布式雷达各阵元与目标间的位置关系校正接收信号相位,再将这些信号相干叠加,对目标形成波束“聚焦”,类似PCA得到虚拟方向图,采用遗传算法优化峰值/旁瓣值得到稀疏线阵;葛桐羽等[11]在设定距离阵列某处目标的方位分辨率不低于某个值的条件下,仍采用PCA来设计近场MIMO线阵;Tian等[12]利用窗函数来降低因基于PCA原理设计的近场MIMO阵列而引发的高旁瓣电平。但是, 当不满足PCA的应用条件, 继续采用原设计则会带来误差,影响成像精度。 即使进行了相位矫正, 或设定方位分辨率、 旁瓣电平等约束, 也只适合于某些特定场合。 当成像目标等发生改变时, 按原条件设计的MIMO雷达线阵需要重新调整。 所以, PCA的近场应用普适性弱。另外, 目前的优化求解算法基本上采用二进制对发射阵列和接收阵列分别编码, 编码长度是发射阵列长度和接收阵列长度的总和。 因为发射阵列和接收阵列的最大长度都等于天线孔径, 所以采用二进制对发射阵列和接收阵列分别编码时, 其编码长度是发射阵列和接收阵列联合编码的2倍, 大大增加了求解空间规模。
鉴于此,本文根据集中式MIMO雷达线阵的特点,研究其近场成像的几何关系,推导其近场信号模型。探讨在天线孔径、最小间距等约束下,阵元数目、方向图的峰值旁瓣比等多个目标的稀疏线阵优化设计方法。
1 近场MIMO雷达线阵的信号模型
1.1 近场MIMO雷达线阵的成像原理
近场MIMO线阵雷达天线信号收发几何关系如图1所示。长度为L的直线阵列沿X方向排列,Y和Z分别表示阵列的探测方向和移动方向。在入射波平面内,m号发射阵元(xm,0,0)到目标P(x0,y0,0)的距离为rm,目标P到n号接收阵元(xn,0,0)的距离为rn。目标P到阵列中心的距离为R,入射角为θ。
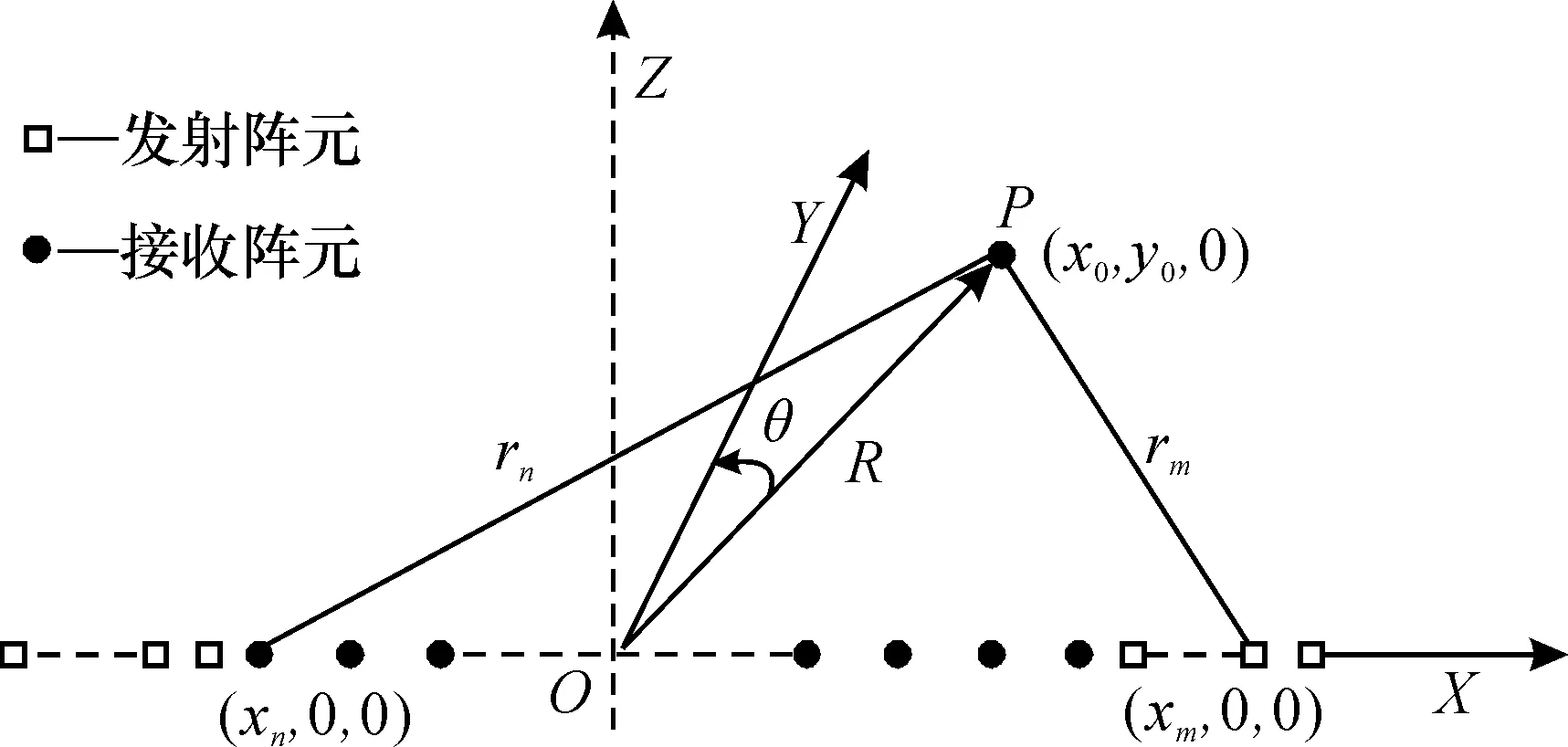
图1 近场MIMO线阵雷达成像几何模型Fig.1 Imaging geometry model of MIMO linear array radar for near field applications
MIMO雷达线阵近场成像的基本原理是: 假设有M个发射阵元和N个接收阵元, 在每个时刻,M个发射阵元同时发出信号, 经目标P反射后被N个接收阵元收集。 线阵天线沿Z轴方向匀速运动, 得到一系列目标信号。 经过处理后, 转换为目标图像。
1.2 近场MIMO雷达线阵的信号模型
如图1所示,线阵和目标位于同一平面,假设各发射阵元同时发射相互正交的窄带信号sm(t),m=1,2,…,M,目标P为各向同性的点目标,则第m号发射阵元发射的信号sm(t),经过目标P反射后,被第n号接收阵元接收的信号sm,n(t)为
(1)
式中:t为信号经历的时间;c为光速;ξm,n为白噪声;ap为目标P的反射系数;Im(λ)为信号的幅值,λ为雷达信号的波长。
rm、rn的计算如下
(2)
(3)
因式中Z坐标为0,所以未列出(下同)。
由于M个发射阵元同时发射的M个信号[sm(t),m=1,2,…,M]相互正交,每个接收单元同时接收到这M个发射信号经目标P反射的回波信号[sm,n(t),m=1,2,…,M;n=1,2,…,N],可通过匹配滤波解调分离出来,再进行累加计算。则M个发射单元和N个接收单元组成的线阵雷达综合信号为
(4)
一般来说,各阵元的结构尺寸和参数完全一致,激励信号也相同,统计独立的高斯白噪声ξm,n,经匹配滤波累加后的均值为0。假设目标的反射系数ap相同,将式(2)、(3)代入式(4)中,得到其归一化方向图为
当目标点距离R确定后,方向图电平值与目标的方位角θ和阵元位置xm、xn有关。
2 近场MIMO雷达线阵稀疏优化设计
2.1 近场MIMO雷达线阵的稀疏优化原理
在近场,不满足下面的条件[10]
R>2D2/λ,
(6)
式中:R为目标距离;D为阵列孔径长度;λ为发射信号波长。
发射阵元、接收阵元与目标的距离差异引起的相位差不能忽略,也就不能采用PCA原理来设计MIMO雷达阵列。
稀疏线阵可看作是从其满阵中删除某些阵元而构成的。为了避免阵元之间的互偶影响,阵元间距d需不小于λ/2。这样,近场MIMO雷达线阵稀疏优化的基本原理为:在给定孔径长度D上,设定一系列间距为d的均匀栅格点;在每个栅格点上,随机放置1个发射/接收阵元,或者不放置阵元;累计该布阵的阵元数目,按式(5)计算此时方向图的峰值旁瓣比。当其达到综合最优时,该阵元放置模式就是稀疏线阵的优化构型。
2.2 近场MIMO雷达线阵稀疏优化的建模
以天线阵元数目最少、方向图的峰值旁瓣比最小为目标,天线孔径长度为D、阵元间距为λ/2等为约束,建立近场MIMO雷达线阵多目标稀疏优化模型:

(7)
式中,xm、xn分别为发射阵元、 接收阵元的X轴坐标。归一化的峰值旁瓣电平(peak side-lobe level, PSLL)是旁瓣电平峰值与主瓣电平峰值比; 最大主瓣电平FCLmax是方位角θ=0°时, 由式(5)计算的归一化方向图F(θ)的值; 而最大旁瓣电平FSLmax计算方法是: 令F(θ)对θ的导数为零, 即F′(θ)=0时, 除θ=0°外,F(θ)的最大值。
2.3 近场MIMO雷达线阵稀疏优化模型的求解
近场MIMO雷达线阵的稀疏优化设计, 是在间距为λ/2的均匀栅格点上, 随机放置1个发射/接收阵元, 达到天线阵元数目M+N最少、 方向图的峰值/旁瓣电平比PSLL最小的目标。 这是一种典型的组合优化问题, 模型的求解空间大, 具有NP-Hard特性, 人工求解计算量巨大, 适合于遗传算法(GA)自动求解。
2.3.1 编码方式 在孔径长度为D的直线上,均匀划分了间距为d的栅格点。算法采用“染色体基因位置按线阵均匀栅格点序排列”的三进制编码方法:g0g1g2…gi…gL-1gL。
染色体长度L大小为天线孔径长度D的线阵上间距λ/2的均匀栅格点数, 即L=2D/λ+1。 染色体共有L个基因位, 基因顺序号为各栅格点编号。 每个位置基因gi取值为0、 1或2, 分别代表“不放置阵元”、 “放置发射阵元”和“放置接收阵元”; 如: 包含5个均匀栅格点线阵的基因编码为20102, 则表示该线阵共有3个阵元, 其中1个发射阵元放在中间栅格点, 2个接收阵元分置两端, 剩下2个栅格点不放置阵元。
2.3.2 适应度函数及选择、 交叉和变异算子 线阵构型设计的目标函数为天线阵元数目最少、 方向图的峰值/旁瓣电平比最小, 故遗传算法中个体k(k=1,2,…,K;K为种群规模)的适值函数定义为
fk=FCLmax/FSLmax。
(8)
采用按比例的适应度分配法进行选择。 个体k的适应度为fk, 则k被复制的概率为
(9)
采用单点交叉法[13]进行染色体交配,个体交叉概率为pc。采用两点交换变异法进行变异操作:按概率pm随机选择2个基因位置,将这2个基因位的基因值进行交换,形成新的染色体。
2.3.3 算法结构 除进行选择、交叉和变异操作外,还进行保留h个具有最佳适应度值个体的复制操作,算法的伪代码为[13]
初始化参数:K、W、pc、pm、h采用随机方法产生初始种群POP0,并计算个体适应度值;
w=0
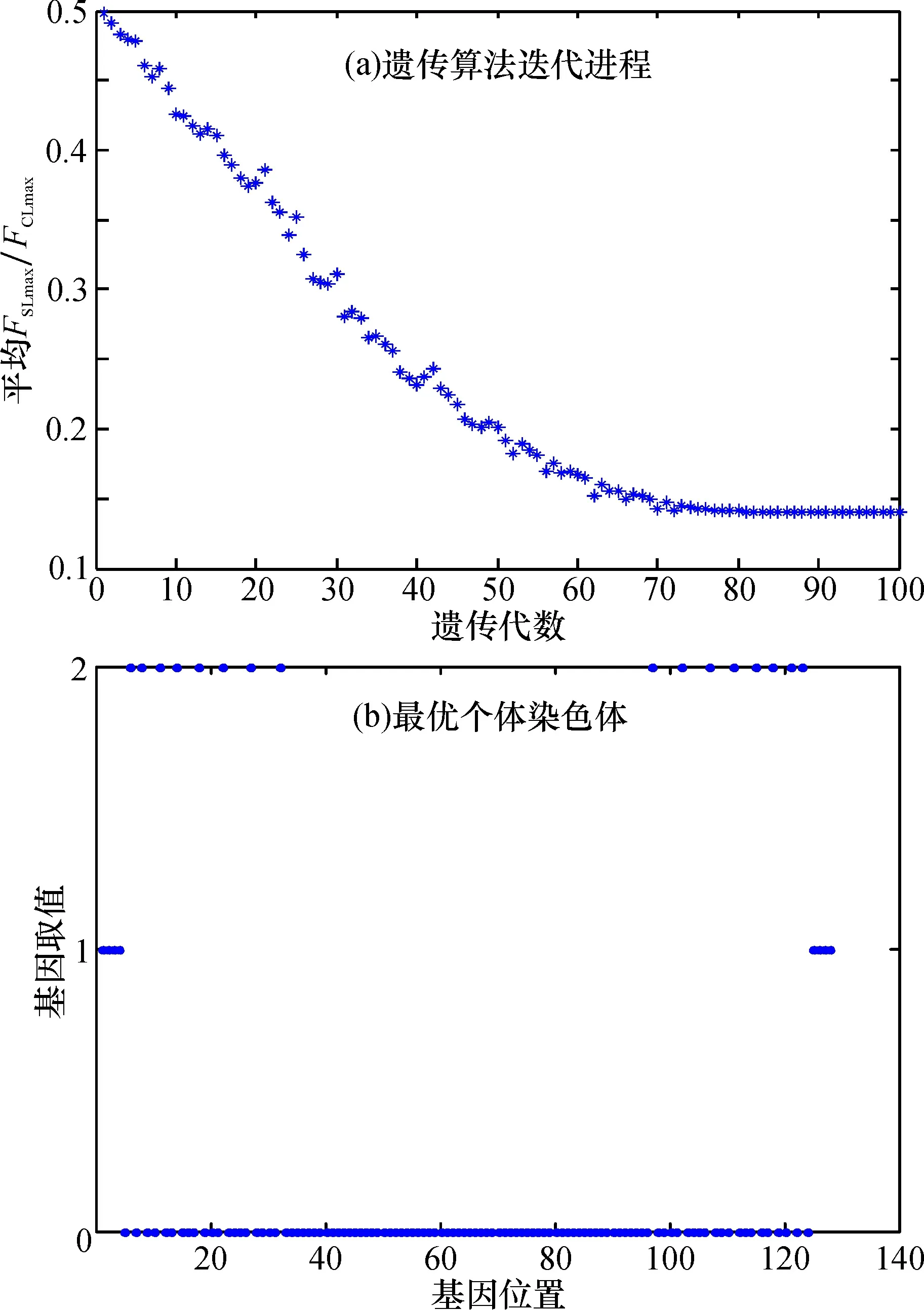
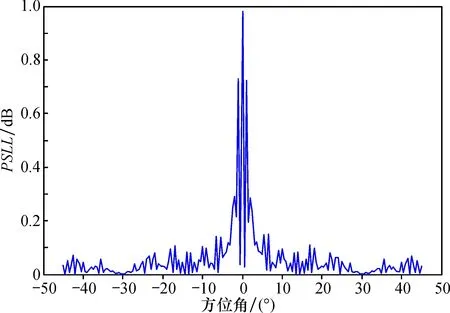
WHILE w 按比例pk复制K*pk个体,进行两两匹配; 对匹配后的个体,按概率pc进行单点交叉操作,生成POPw′; 按概率pm对POPw′进行变异操作,生成POPw″; 计算POPw″个体的适应度值; 从POPw中选择h个最优个体,从POPw″选择K-h个最优个体形成POPw+1 w=w+1 END WHILE; 输出POPw中适应度值最好的个体。 假设某MIMO线阵雷达监测场合,已根据目标的距离R=30~120 m、范围(-45°, 45°)和元器件等情况,确定雷达波长λ=0.018 m,天线孔径D=1.143 m。现需要优化设计该线阵,并要求阵元间最小间距d=λ/2=9 mm。 因2D2/λ=2×1.1432/0.018=145.161 m, 大于120 m,远场PCA原理的条件不满足,需要按近场来建立成像信号模型,并进行方向图函数的计算等。 在MIMO天线稀疏阵列设计中, 希望得到等效为满阵收发阵元对, 或者说发射阵元数与接收阵元的乘积等于均匀栅格点数, 即M·N=D/d+1,M、N为正整数。另外,线阵天线阵列的对称性要求M和N是偶数,且接收阵元数目N一般不小于发射阵元数目M。 在本例中, 满足M·N=128等条件的(M,N)为(2,64)、 (4,32)和(8,16)。 显然, 在这3组数目中,M=8、N=16时,M+N=24为最小阵元数目。这样,可以构建MIMO雷达线阵稀疏优化设计模型为 (10) 式中:M=8,N=16,D=1.143 m,d=9 mm。 根据MIMO线阵雷达成像几何关系图, 将X坐标上天线孔径栅格点, 从左到右顺序排列。 如图2所示。 图2 MIMO线阵栅格点排序及阵元X坐标点Fig.2 Grid points of MIMO linear array and X coordinate points of array elements 设i为栅格点序号,im为第m号发射阵元所在的栅格点序号,in为第n号接收阵元所在的栅格点序号, 则栅格点i的X轴坐标为xi=i·d-D/2; 同理, 发射阵元和接收阵元的X轴坐标分别为xm=im·d-D/2和xn=in·d-D/2。 其中,i、im和in的取值为0至127(D/d)之间的正整数。 这样, MIMO雷达线阵稀疏优化设计的模型式具体化为 (11) 3.3.1 染色体编码及适应度函数 由于MIMO雷达线阵长度D=1 143 mm,阵元的最小间距d=9 mm,则共有D/d+1=128个满阵栅格点,所以染色体总长度为128。采用三进制编码,则染色体数总共有3128,约1.179×1061个染色体,规模大。若采用常规的发射阵列和接收阵列分置的二进制编码,染色体长度为三进制编码的2倍,即256,这时染色体数总共有2256,约1.158×1077个染色体,规模更大。 按g0g1g2…gi…gL-1gL所示的染色体基因编码方式,若gi=1, 则im=i,xm=0.009im-0.571 5; 若gi=2, 则in=i,xn=0.009in-0.571 5。 代入式(5), 得到 (12) 线阵构型设计的另一个目标函数是方向图的峰值旁瓣比最小, 即求F(θ)随着目标的方向角θ变化时,其第一个栅瓣峰值电平FSLmax与最大主峰电平FCLmax的比值,设其倒数为遗传算法中个体适值函数。 3.3.2 主要操作算子程序 本例为三进制整数组合优化。一般来说,MIMO雷达线阵常采用中心点对称结构,所以只需要进行一半,即64个栅格点的组合优化求解后,另一半采用镜像操作就组成了整个线阵。这时,染色体总数为364=3.434×1030,规模大大减少。其中,交叉操作算子和变异操作算子的MATLAB程序关键代码如下: (1)单点交叉操作函数 Function crs1p() ncrsKds%计算交叉子辈数 index=0 for k=1:ncrsKds/2 index=index+1; pnt1=pnts(index,:)%选择1个父个体 index=index+1; pnt2=pnts(index,:)%选择另1父个体 csite=ceil(rand*63+1)%选择交叉点 crsKds(i,128)=[pnt1(1:csite),pnt2((csite+1:128-csite), pnt1(129-csite:128)]%产生1个子个体 crsKds(i+ncrsKds/2,128)=[pnt2(1:csite),pnt1((csite+1:128-csite), pnt2(129-csite:128)]%产生另1个子个体 while ((M~=8),(N~=16),…) %判断是否满足M=8和N=16等约束条件?若不满足,则重新产生子个体。 csite=ceil(rand*63+1)重新选择交叉点 crsKds(i,128)=[pnt1(1:csite),pnt2((csite+1:128-csite), pnt1(129-csite:128)]重新产生1个子个体 crsKds(i+ncrsKds/2,128)=[pnt2(1:csite),pnt1((csite+1:128-csite), pnt2(129-csite:128)]%重新产生另1子个体 end end (2)两点交换变异操作函数 function mtnsp() ntnKds%计算变异子辈数 for k=1:nmtnKds mpnt=pnts(round(rand*(pop-size-1))+1,:)%选择1个父个体 P1=find(rand(1,32) P2=find(rand(3364) mtnpnt(1,:)=[mtnpnt(1:(p1-1)),mtnpnt(p2),mtnpnt((p1+1):(p2-1)),mtnpnt(p1),mtnpnt((p2+1):(128-p2)),mtnpnt(p1),mtnpnt((130-p2):(128-p1)), mtnpnt(p2),mtnpnt((130-p1):128)]%变异操作 mtnKds(i,:)=mtnpnt %产生1个子个体 end 3.3.3 MATLAB仿真及分析 种群规模K取200,迭代次数W取100,交叉概率pc取0.8,变异概率pm取0.05,直接进入下一代优良个体数h取10。在MATLAB中编写GA程序,对本算例进行仿真测试。运行结果如图3所示。 其中,图3a为平均FSLmax/FCLmax;图3b为遗传算法求解后的最优个体“111102020020020002000200002000020000000000000000000000000000000000000000000000000000000000000000020000200002000200020020020201111”,表示在“1,2,3,4,125,126,127,128”栅格点放置了8个发射阵元,在“6,8, 11,14,18,22,27,32,97,102,107,111,115,118,121,123”栅格点放置了16个接收阵元峰值旁瓣电平比PSLL=-17.016 dB。 按照此线阵布局,以对距离R=60 m、方位角(-45°,45°)的目标监测为例,用MATLAB计算绘制的归一化方向图如图4所示。 归一化主瓣峰值为1, 最大归一化副瓣峰值为0.141, 即-17.016 dB; 按-3 dB主瓣宽度为(-2.5°,2.5°)。 表明本文的阵列优化算法可行。 图3 算例仿真运行结果Fig.3 Results of GA solving for the example 图4 算例优化线阵归一化方向图Fig.4 Optimization linear array normalization pattern MIMO线阵雷达的近场监测理论与应用是目前的热点问题,直线阵列的构型决定了其成像模式,线阵的稀疏优化设计成为了重要的研究课题。 由于雷达近场应用不满足相位中心近似PCA原理,本文根据成像的几何关系,直接推导近场信号的函数表达式, 进而建立在天线孔径、 最小间距的约束下的线阵稀疏优化模型,再采用“染色体按三进制编码”的遗传算法求解,得到阵元数目、峰值旁瓣比最优的线阵构型。 算例仿真与分析表明,本文所建模型及其求解原理可行,具有较好的实用参考价值。经信号模型等相应变更,还可用于近场MIMO雷达面阵的稀疏优化设计。3 算例分析
3.1 问题描述
3.2 MIMO雷达线阵稀疏优化设计的建模
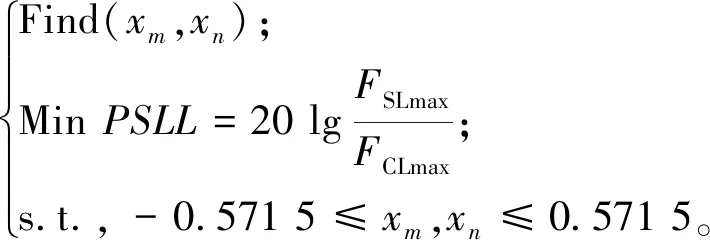

3.3 MIMO雷达线阵稀疏优化模型的GA求解
4 结束语
