基于DoG算子的年轮图像边缘提取及树龄测量方法

张 露， 郭清宇， 梁静静， 刘卫光

(中原工学院 计算机学院， 河南 郑州 450007)

树木是人类生态环境的重要组成部分，它的生长过程与气候环境变化息息相关，不同的光照、气温、降水量等会造成树木年轮的差异。树木的年轮常作为测定一颗树的树龄的依据。由于树木年轮具有易于获取、分辨率高、连续性强、定年准确等特点，其广泛应用于树木年代学、生态学和城市树木存活质量研究等方面[1-2]。传统的树龄分析方法主要采用人工读取年轮数、年轮宽度等参数值，这种处理方法复杂繁琐、效率低下、容易出现误差，尤其针对大量样本时，测量的准确性会大大下降。

随着计算机视觉学科的快速发展，利用该学科中的图像处理技术(包括灰度化、图像滤波、边缘提取、图像分割等)对年轮图像进行处理，可得到年轮参数[3]。CERDA等提出了一种高效的年轮提取方法，该方法对噪声有较强的抗干扰性，可以有效地提取年轮图像的轮环[4]。MEENAKSHISUNDARI等对比了Sobel、Prewitt、Roberts、Canny等算子对年轮图像的提取效果，发现使用Canny算子从年轮图像中提取轮环的效果较好[5]。NORELL设计开发了一个可以自动检测识别年轮轮环的系统，利用图像处理技术自动完成对年轮数的统计[6]。赵娟娟等将数字图像处理技术与AutoCAD结合，有效地对年轮宽度进行了测量[7]。陈佶将统计学中的知识应用到图像处理中，相比传统方法，其准确率得到了显著提升[8]。王燕凤等对Canny算子进行了改进，结合双边滤波算法对年轮边缘进行提取，得到了清晰、光滑、准确的年轮边缘；并提出了一种基于多数投票的树龄统计方法[9]。朱琪对图像预处理算法进行了改进，并结合自动区域生长算法直接实现了对彩色年轮图像的分割，快速有效地提取到轮环[10-11]。

本文基于DoG(Different-of-Gaussian)算子，对高斯滤波卷积时的运算方式进行改进，对比不同尺寸的高斯卷积核对年轮图像的处理效果，并通过对年轮图像中的边缘数量进行统计，实现树龄测量。

1 树木年轮的数字图像特征

年轮是树木在生长过程中形成的。一年四季中，由于春夏季节雨水较多，树木生长较快，形成层快速分化，该阶段所形成的木质被称为早材(也叫春材)；进入秋冬季节后，雨水减少，树木生长变慢，形成层分化变慢，该阶段所生成的木质较少且颜色变深，被称为晚材(也叫秋材)。图1所示为树木的部分年轮图，中间的圆环部分为髓心，早材、晚材在髓心外围交替出现，形成不规则的轮环，早材、晚材加起来即是一个完整的年轮。在树木生长过程中，前一年生成的晚材和后一年生成的早材在颜色上会有一条明显的区别线，该区别线即为年轮线。两条相邻的年轮线构成一个完整的年轮。对年轮图像的研究就是利用图像处理技术(灰度化、图像滤波、边缘提取等)完成对年轮线的提取，从而更方便地统计年轮数、年轮宽度等参数。但通常情况下，获取的年轮图像会受到锯痕、色斑、节子等因素的影响，给提取年轮线带来困难。

图1 年轮图像示意图

2 相关理论

2.1 高斯滤波

在计算机视觉中，二维高斯滤波使用的高斯函数为两个一维高斯函数的乘积，其中两个一维高斯函数的标准差σ通常相同，形式如下：

(1)

(2)

其中：式(1)表示一维高斯函数；式(2)表示二维高斯函数；σ为标准差，通过调整σ的值可以调整周围像素对当前像素的影响程度。

对图像进行高斯滤波，就是用某一尺寸的高斯卷积核与要处理的图像进行卷积运算，遍历整个图像，形式如下：

g(x,y)=G(x,y)*f(x,y)

(3)

式中：f(x,y)表示要处理的图像；G(x,y)表示高斯卷积核；*表示卷积操作；g(x,y)表示卷积后的图像。

2.2 高斯差分(DoG)算子

DoG(Difference of Gaussian)是高斯函数的差分，Gaussian是一个正态分布函数。在数字图像中，图像边缘的形成通常是由于图像中相邻像素的灰度值突然变化所致。通过在不同参数下对图像进行滤波处理，可得到边缘灰度值不同的图像，相减即可得到DoG算子的响应图像，进而得到图像的边缘[12]。

在DoG算子中，高斯函数定义同式(2)。

用参数值分别为σ1、σ2的高斯函数与要处理的图像f(x,y)进行卷积操作，可以得到如下两幅图像：

g1(x,y)=Gσ1(x,y)*f(x,y)

(4)

g2(x,y)=Gσ2(x,y)*f(x,y)

(5)

将g1(x,y)和g2(x,y)相减，可得响应图像F(x,y)：

F(x,y)=g1(x,y)-g2(x,y)=

Gσ1(x,y)*f(x,y)-Gσ2(x,y)*f(x,y)=

(Gσ1(x,y)-Gσ2(x,y))*f(x,y)=

DoG*f(x,y)

(6)

所以，DoG算子可以表示为：

(7)

利用DoG算子进行边缘提取，其流程如图2所示[13]。

2.3 改进的高斯滤波算法

通过滤波算法，可以对图像进行增强。对于高斯滤波，卷积核的大小和图像增强效果有直接的关系。若选择的卷积核过小，则噪声处理效果不好；若卷积核过大，则会造成图像边缘模糊、运算量大、算法时间复杂度高等问题。

本文将对高斯滤波算法的运算过程进行改进，对图像作二维高斯滤波，设卷积核的半径为r，结合式(1)—式(3)可得：

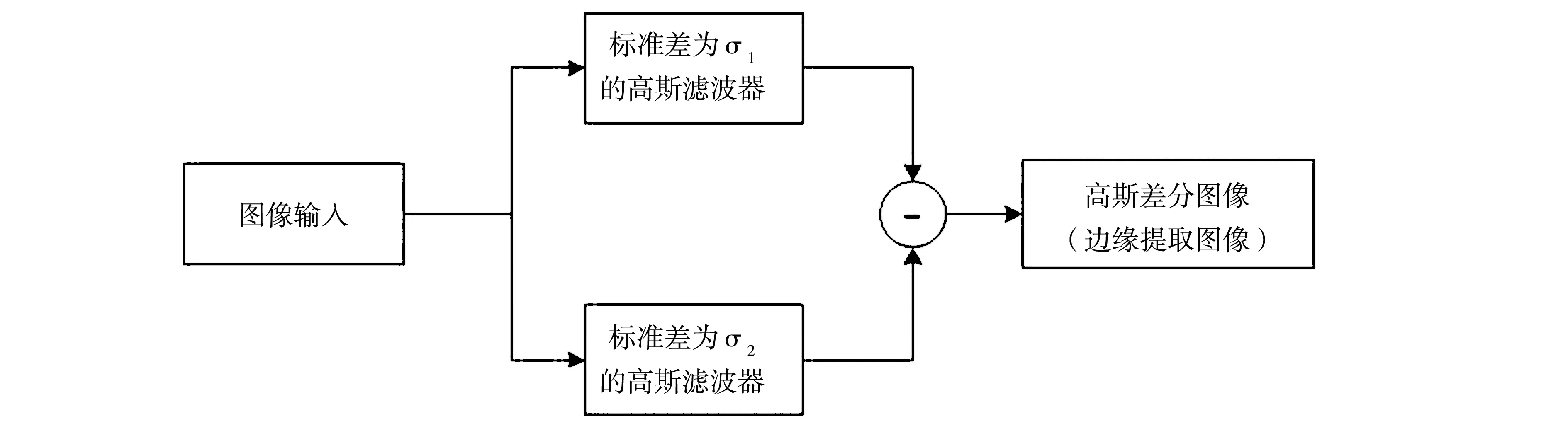
图2 DoG边缘提取流程图

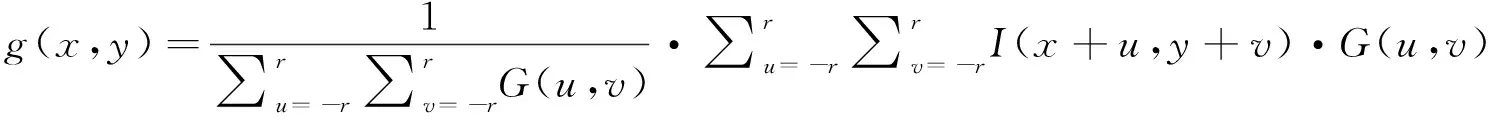
(8)

式中，I(x+u,y+v)表示领域中像素的灰度值。

对于M×N大小的图像f(x,y)，卷积核的大小为(2r+1)×(2r+1)，由式(8)可知，需要进行(2r+1)×(2r+1)×M×N次乘法和((2r+1)×(2r+1)-1)×M×N次加法操作。将式(8)的计算过程进行转化，可得：

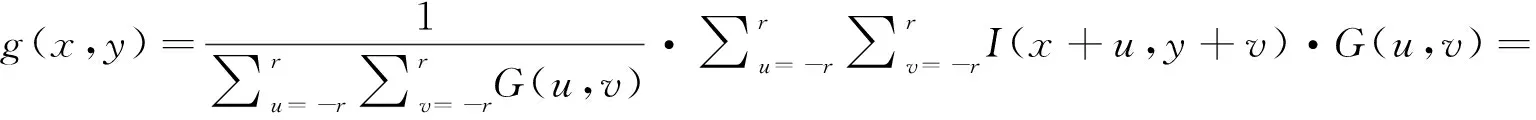
(9)

由式(9)可知，二维高斯滤波的计算过程，可以转换为先在水平方向上做一维高斯卷积运算，再在运算结果上做竖直方向上的一维高斯卷积运算。这样对于M×N大小的图像f(x,y)来说，需要进行(2r+1)×2×M×N次乘法和(2r+1-1)×2×M×N次加法操作，算法时间度是之前的2/(2×r+1)，降低了运算复杂度。与传统的高斯滤波算法相比，该算法减少了运算次数，时间复杂度得到了优化。

3 实验与分析

3.1 实验数据

选取3张不同的树木年轮图片(见图3)进行实验。在利用DoG算子对样本图像进行边缘提取前，需要先对其进行预处理，将其转化为灰度图像(见图4)。

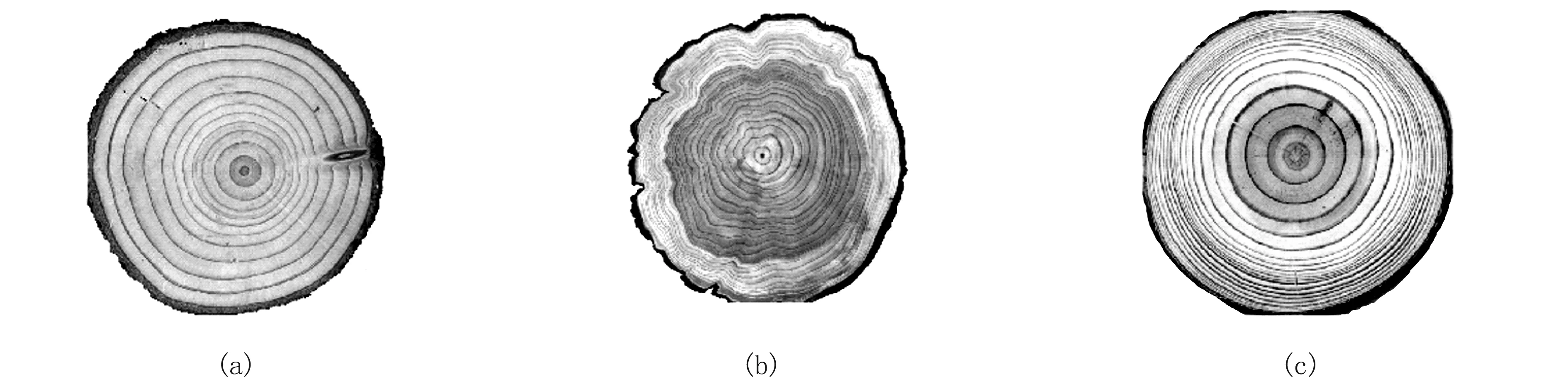
图3 样本图像

图4 灰度化后的图像

3.2 实验结果与分析

使用DoG算子对图4中灰度化后的年轮图像进行边缘提取操作，得到的结果如图5—图7所示，其中卷积核的大小分别为5×5、3×3、7×7，σ1=0.8，σ2=1 。图5—图7中(b)、(c)分别为图4中(b)、(c)经实验处理后部分放大的效果图，从中可以看到年轮线被很好地提取出来。

图5 卷积核大小为5×5的年轮边缘提取图像

图6 卷积核大小为3×3的年轮边缘提取图像

图7 卷积核大小为7×7的年轮边缘提取图像

对比图5与图6可以看出，当卷积核的尺寸较小时，经DoG算子处理后，依然存在较多的噪声，这对后续的年轮参数的提取有可能造成影响。对比图5和图7可以看出，图像处理效果大致相同，但由于卷积核变大，运算量增加，处理速度变慢。所以，本文在年轮图像边缘提取时选择5×5大小的卷积核。

3.3 树龄测量

在年轮图像中，对树龄的测量就是对图像边缘数量的统计。通过前面的实验，可有效提取到年轮图像的边缘。以图3(c)为例，对提取到的边缘图像截取以髓心为中心的矩形图像(见图8)，用于对树木年轮数的统计，具体流程为：

图8 统计年轮数图像

(1) 对图8进行二值化处理，记为BW；

(2) 获取BW对应矩阵的行数、列数，分别记为m、n(BW对应的部分图像矩阵如图9所示)；

(3) 对矩阵中每行值连续为1的部分(如图9中矩形框所示)进行个数统计，记为Ni；

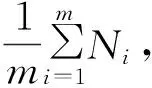
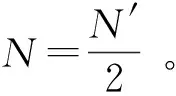
通过计算，最终测得N=20，即年轮数为20，与实际情况相同。

图9 图像矩阵

4 结语

本文根据树木年轮的图像特征，提出了基于DoG算子的年轮图像边缘提取方法及树龄测量方法；对高斯滤波的运算过程进行改进，采用5×5大小的卷积核，优化了因卷积核大小不合适导致的噪声多、运算量大、处理速度慢等问题。实验结果表明，利用DoG算子可以有效地提取年轮边缘图像；利用图像矩阵的相关理论对图像边缘数量进行统计，可以准确测量树龄。但本算法对于由锯痕较多引起的年轮线模糊的图像，不能很好地提取边缘图像，还有待改进。