ARIMA季节乘积模型在新疆地区细菌性痢疾发病率预测中的应用

沈彭 魏峰

(安徽大学经济学院， 合肥 230039)

细菌性痢疾是新疆地区的高发传染病，其发病率长期位列该地区甲、乙类传染病发病率前五名。防范细菌性痢疾仍是该地区疾病防控工作的重点之一。为了从根本上做好疾病防控工作，学者们开始从传染病的流行规律及预测方法等方面着手进行研究。国内已有学者利用时间序列模型对区域内的疾病发生规律进行预测，短期数据的预测效果较好[1-5]。本次研究拟利用新疆法定传染病报告中细菌性痢疾的月发病率资料分析其时间变化趋势，应用ARIMA (Autoregressive Integrated Moving Average Model，即求和自回归移动平均模型)季节乘积模型对其进行拟合和预测，探讨将该模型用于细菌性痢疾疫情预测预警的可行性。

1 数据准备与建模方法

1.1 数据准备

数据为新疆地区2004 — 2016年细菌性痢疾月发病率，由中国疾病预防控制中心子网站 —— 公共卫生科学数据中心披露[6]。其中，取2004年1月 — 2016年4月份的数据用于建立模型，取2016年4月至12月的数据用于预测值分析比较。ARIMA季节乘积模型对于数据的短期预测比较灵敏，所以只保留8个月的数据用于实际值与预测值的对比检验。

1.2 ARIMA季节乘积模型的建立

ARIMA模型又称Box-Jenkins模型，该分析方法是一种时间序列预测方法，用于描述非平稳性资料。当时间序列中存在各种趋势性或季节波动性时，可以建立连续模型ARIMA(p，d，q)或季节模型ARIMA(P，D，Q)S。有的季节性时间序列不仅含有季节性成分，还混有非季节性成分，此时可将两者的混合效应相乘，构建ARIMA季节乘积模型ARIMA(p，d，q)(P，D，Q)S。其中，p、q分别为自回归阶数和移动平均阶数，P、Q分别为季节性自回归阶数和移动平均阶数，d为差分次数，D为季节性差分次数，S为季节周期步长。模型结构通常为：

(1)

式中：θ(B)为连续模型的q阶移动平均系数多项式；φ(B)为连续模型的p阶自回归系数多项式；θS(B)为季节模型的q阶移动平均系数多项式；φS(B)为季节模型的p阶自回归系数多项式。按以下流程建立模型(见图1)[7]。

图1 ARIMA模型建立流程

1.3 模型建立流程

(1) 数据预处理。在获得一组观察序列后，首先进行平稳性和白噪声检验。根据时序图、(偏)自相关图对数据的平稳性作出初步判断，并进行PP单位根检验(PP)、Dickey-Fuller单位根检验(DF)或增广Dickey-Fuller单位根检验(ADF)。对于白噪声检验，则通过Q值或QLB统计量的P值进行判断。平稳非白噪声序列可进入模型拟合阶段，非平稳序列需进行平稳化处理，白噪声序列则不能进行模型拟合。

(2) 数据平稳化处理。通过一般差分与季节差分消除趋势和季节的影响，并确定d、D值，差分后的序列需再次通过平稳性和白噪声的检验。

(3) 模型识别。根据差分过程和结果，确定带有季节因子的乘积模型ARIMA(p，d，q)(P，D，Q)S的基本形式，从低阶到高阶逐次完成模型的检验识别。

(4) 参数估计与模型检验。选用各参数有统计学意义以及AIC值、BIC值较小的适用模型进行模型拟合，并对模型拟合结果进行诊断，判断残差是否为白噪声序列，从而确定模型的拟合优度。

(5) 模型预测。利用完成拟合的模型进行数据预测，并对预测结果进行评价。

(6) 统计分析。应用统计学软件SAS 9.4完成数据处理、模型识别、模型预测等。

2 模型处理结果

2.1 数据预处理

图2所示为新疆地区2004年1月 — 2016年4月细菌性痢疾月发病率时序图。每年4月份的数据存在明显的季节性变化趋势，每年5月 — 9月发病率曲线处于波峰位置，为发病高峰期。图3所示为2004年1月 — 2016年4月新疆细菌性痢疾月发病率自相关图，其自相关系数也呈现出周期性的变化规律。

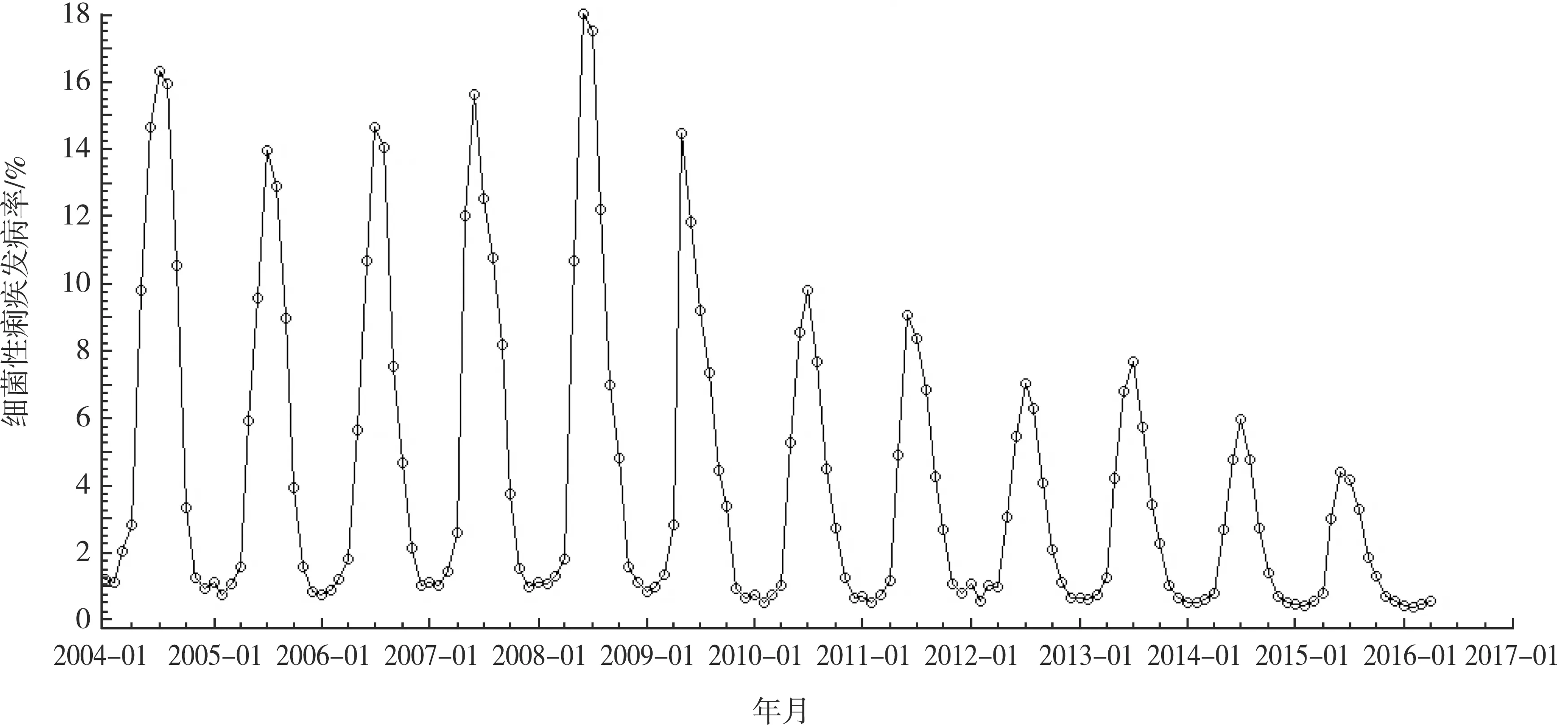
图2 2004年1月 — 2016年4月新疆地区细菌性痢疾月发病率时序图

2.2 数据平稳化处理

根据数据特征，对原始序列进行季节差分处理。差分后的自相关图(见图4)显示，原序列的周期性趋势消失； ADF检验的结果(见图5)显示，差分过后P值均小于0.05，季节差分后的序列可以确定为平稳序列。

2.3 白噪声检验

对季节差分后的序列延迟6、12、18、24期进行白噪声检验(见图6)，获得的QLB统计量的P值均小于0.01，说明差分后的序列是非随机的。

图3 2004年1月 — 2016年4月新疆细菌性痢疾月发病率自相关图

图4 2004年1月 — 2016年4月新疆细菌性痢疾月发病率季节差分后自相关图

图5 季节差分后ADF检验结果

图6 季节差分后白噪声检验的结果

2.4 模型识别

根据差分过程及其结果可知，季节差分1次，季节步长为12，确定适合细菌性痢疾月发病率序列的模型初步形式为：ARIMA(p,0,q)×(P,1,Q)12。

首先对连续性模型的p、q进行识别，由表1可知，BIC(0,1) = 0.814 058为最小。选择ARIMA(0,0,1)为连续模型ARIMA(p,0,q)的最优模型。

表1 不同p、q值情况下ARIMA(p,0,q)模型的BIC值

在连续模型的基础上，对季节模型的P、Q进行识别，从低阶到高阶逐个进行尝试，分别比较ARIMA(0,0,1)(0,1,0)12、ARIMA(0,0,1)(0,1,1)12、ARIMA(0,0,1)(1,1,0)12、ARIMA(0,0,1)(1,1,1)12、ARIMA(0,0,1)(0,1,2)12等模型的拟合优度。在表2中，ARIMA(0,0,1)(0,1,0)12模型的AIC值和SBC值较小(AIC值为502.973 4,SBC值为508.798 7)，为相对最优模型。

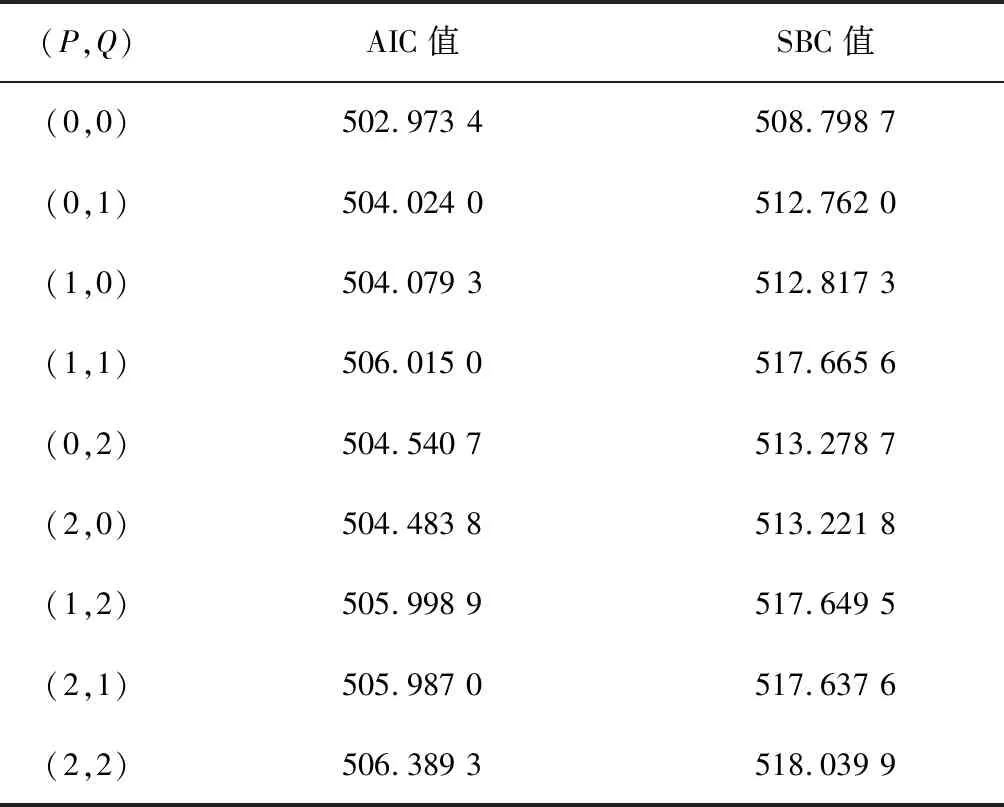
表2 不同P、Q值情况下ARIMA(P,1,Q)12模型的AIC值和SBC值

2.5 参数估计与模型检验

如图7所示，对常数项、MA(1，1)的估计值(-0.430 5、-0.653 4)进行显著性检验，它们均具有统计学意义(P<0.05)，可以判定以下最终获得的ARIMA(0,0,1)(0,1,0)12模型是恰当的。

图7 参数估计与模型检验结果

2.6 模型预测

用ARIMA(0,0,1)(0,1,0)12模型预测新疆地区2016年5月 — 12月细菌性痢疾的月发病率，结果如图8所示。图中，拟合值与实际值基本重合，说明模型对原始序列信息提取比较充分，拟合效果比较好；同时，预测值的变化趋势与实际值基本一致，实际值基本落在预测曲线95%的可信区间内。预测结果见表3。

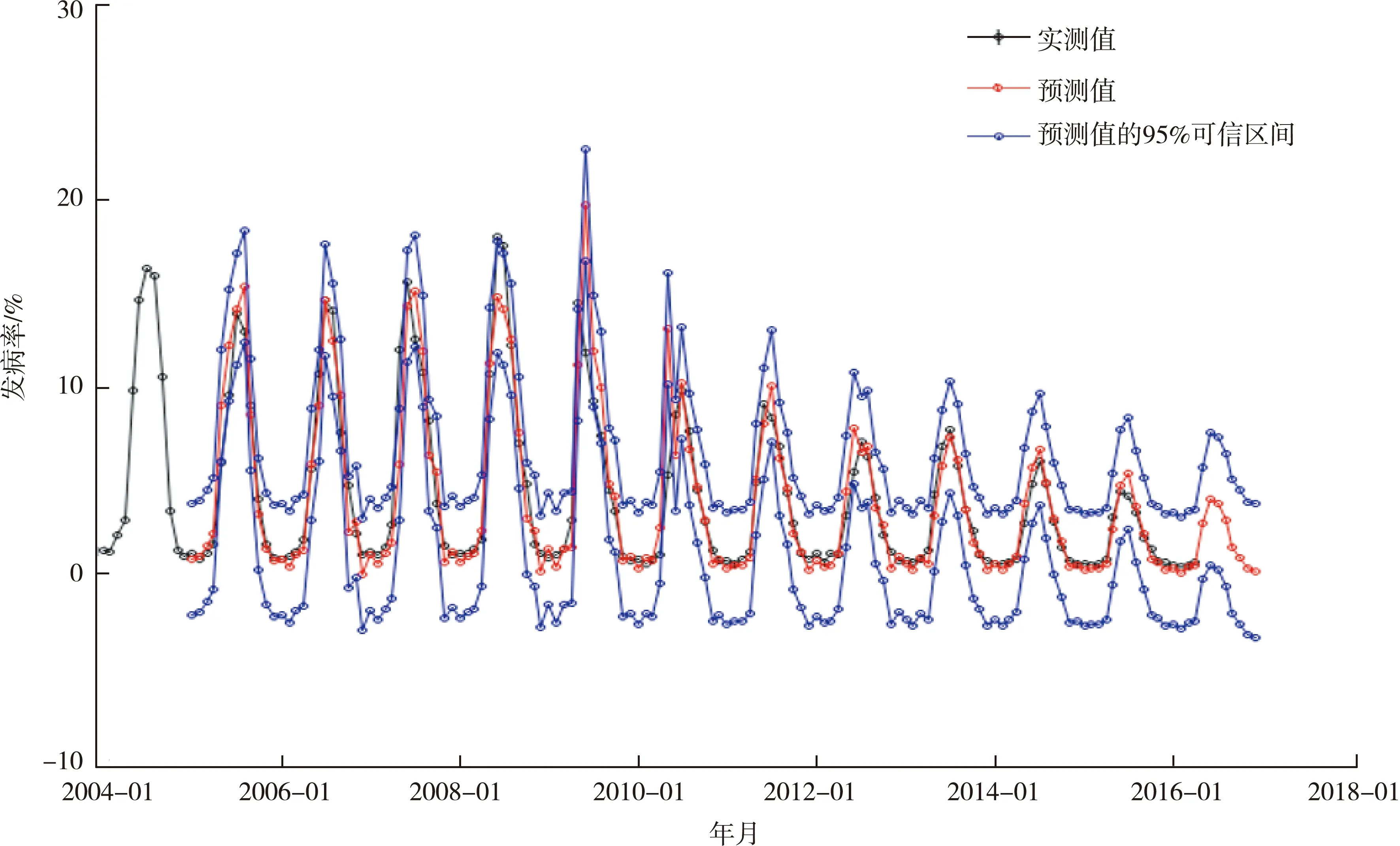
图8 ARIMA(0,0,1)(0,1,0)12模型拟合的新疆细菌性痢疾月发病率

表3 2016年5～12月新疆细菌性痢疾月发病率预测结果

3 讨论

在实际应用中，数据的时间序列大多是不平稳的，表现出各种趋势性或季节波动性。有的季节性时间序列不仅含有季节性成分，还混有非季节性成分，若采用简单的时间序列模型进行分析，往往不能得出准确的预测结果。建立ARIMA季节乘积模型，可根据预测变量自身在各时刻变化规律的依存关系，以时间因素综合替代各种影响因素，反映出疾病发生的趋势性、周期性及季节性[8]。

本次研究中，以新疆地区2004年1月 — 2016年4月细菌性痢疾月报告发病率数据为基础，拟合ARIMA季节乘积模型，同时对2016年5 — 12月的数据进行了预测及比较。研究结果表明，采用ARIMA(0,0,1)(0,1,0)12模型拟合所得到的细菌性痢疾月发病率与实际报告数据基本重合，说明模型对原始序列信息的提取比较充分；同时，预测值的变化趋势与实际值变化一致，实际值基本落在预测曲线95%的可信区间内。利用ARIMA季节乘积模型对新疆地区细菌性痢疾月报告发病率数据进行拟合和预测，是合理可行的。

2010 — 2016年细菌性痢疾月报告发病率整体上低于2004 — 2009年的同期水平，特别是2012年最低，这可能与监测方案的调整有关。因此，2012年发病高峰处预测值和真实值之间存在一定的差异，预测值要高于真实值。这一局限性决定了通过单次分析结果所建立的模型，需要不断加入新的实际值，以修正或重新拟合才能更准确地反映实际情况[9]。