依据水驱前缘移动规律优化分层注采压差

朱圣举 朱洁 安小平 张皎生

(1. 中国石油长庆油田分公司勘探开发研究院， 西安 710018； 2. 低渗透油气田勘探开发国家工程实验室， 西安 710018；3. 中国石油长庆油田分公司第六采气厂， 西安 710018)

由于渗透率、岩性、沉积环境、流体性质等因素有所差别，因而油层间在纵向上会表现出非均质性[1]。在合注合采的情况下，各油层也会由于吸水能力、水线推进速度、分层采液能力、层间动用程度等方面的差异而产生层间矛盾。技术人员围绕层间矛盾及其解决办法进行了许多探索。于春生等人通过室内实验对纵向非均质性进行了研究[2-4]。卜亚辉等人对纵向非均质性的评价方法进行了研究[5]。沈瑞等人对纵向水驱波及系数进行了研究[6]。张顺康等人对多层油藏水驱开发理论模型进行了研究[7]。陈永生从实践的角度进行了经验性的探索[8-10]。然而，这些研究大多未对层间突进规律进行定量描述。丘勇松等人曾对层间突进规律进行了探索[11-12]，但并未考虑水驱前缘问题，且其假定条件为两层共用一个注采压力系统，这显然不利于调整层间矛盾。在文献[13]的研究中，虽然考虑了水驱前缘问题，但仅限于平面注采压差的调整，并未探讨层间注采压差的调整。

本次研究将基于水驱油藏基本渗流理论，运用数学解析法，建立径向渗流条件下的分层注采压差优化模型。

1 分层注采压差优化模型的建立

在图1所示平面径向渗流示意图中，可以看到平面径向渗流俯视图及上下两层平面径向渗流图。

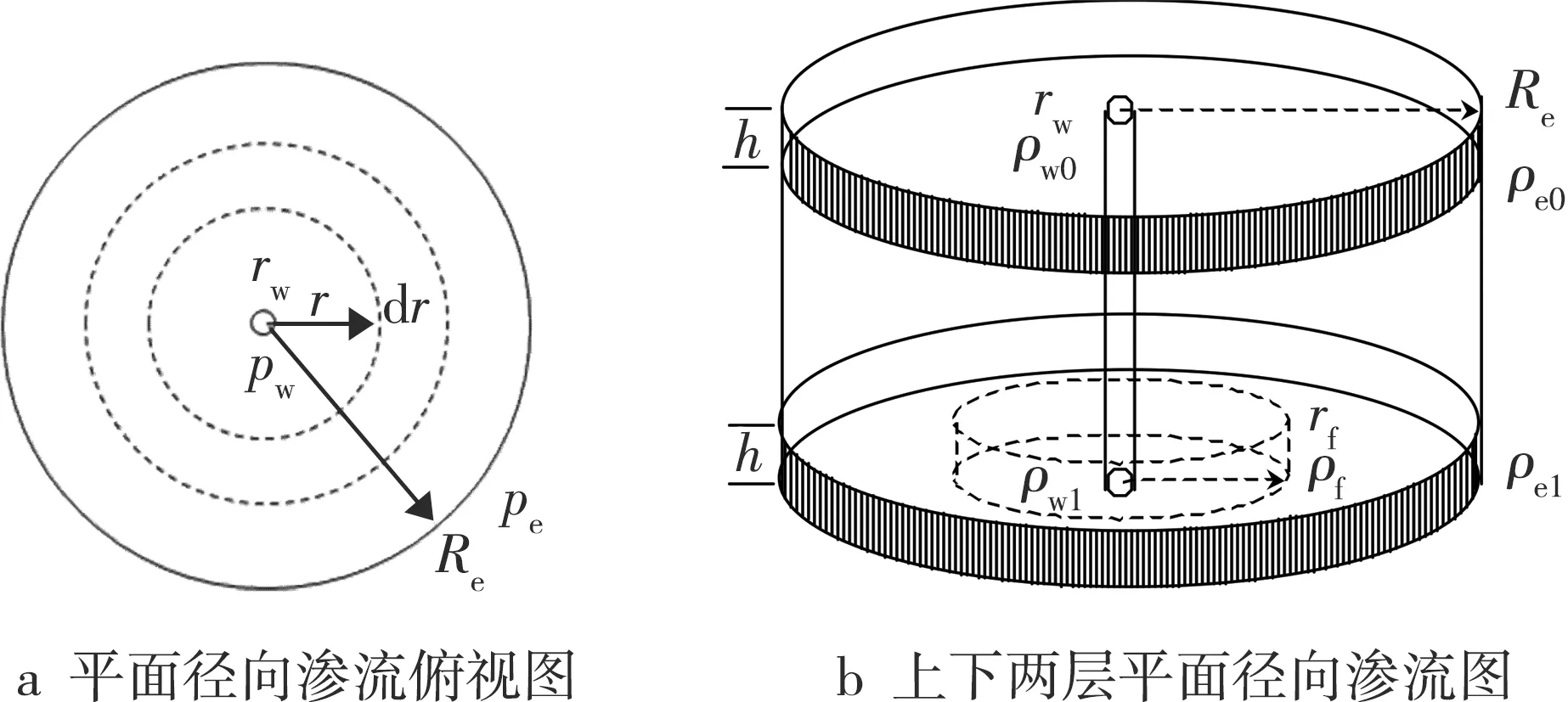
图1 平面径向渗流示意图

取微元dr，计算截面处(r)的日流量为[14]：

(1)

式中：q—— 截面处(r)的日流量，m3；

C—— 常数，0.086 4；

K—— 储集层渗透率，10-3μm2；

μw—— 注入水的地下黏度，mPa·s；

Re—— 平面径向渗流泄油半径，m；

rw—— 井筒半径，m；

pe—— 注入端(Re处)地层压力，MPa；

pw—— 采出端(rw处)的地层压力，MPa；

r—— 流线长度(半径)，m；

A(r) —— 流线长度r处的流管截面积，m2。

截面(r)处的渗流单元关系式为[14]：

(2)

式中：φ—— 储集层孔隙度，无因次；

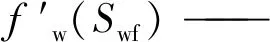
t—— 水驱前缘移动的时间，d。

当平面径向稳定渗流时，对式(1)进行积分，得到式(3)：

(3)

式中：h—— 储集层厚度，m。

将式(3)代入式(2)，并取积分上下限，得：

(4)

式中：rf—— 水驱前缘所处位置(半径)，m。

对式(4)取积分，得小层平面径向渗流的水驱前缘位置(rf)随时间(t)变化的函数关系：

(5)

对式(5)两边时间(t)同时求导，得：

(6)

式中：vrf—— 水驱前缘移动到rf处的移动速率，md。

如图1所示，设有上、下2个小层，在各参数中分别用下标“0”和“1”表示。假设，K0>K1，两层互不连通，注入水同时从Re处开始驱油；同时，两层均处于稳定渗流状态，分层产液量及注采压差保持稳定。

要使两层的水驱前缘同时到达采出端，则必须满足的条件是：在同一时刻(t)，两小层的水驱前缘位置rf必须相等，即rf0=rf1；在同一前缘位置(rf)，两小层的水驱前缘移动速率(vrf)必须相等，即vrf0=vrf1。

(7)

Δp1=pe1-pw1

Δp0=pe0-pw0

式中： Δp1——“1”号小层的注采压差，MPa;

Δp0—— “0”号小层的注采压差，MPa。

令

(8)

式中：m—— “1”号小层与“0”号小层的储渗参数之比，无因次。

将式(8)代入式(7)，即得注采压差优化模型：

(9)

此注采压差优化模型的意义在于，根据层间储渗参数之比来优化分层注采压差。满足分层注采压差之比与分层储渗参数之比的乘积等于1时的分层注采压差，即为最佳注采压差。

2 现场应用分析

以鄂尔多斯盆地某砂岩油藏为例进行现场应用分析。该油藏生产层位为延安组，细分为“0”号和“1”号两小层，其中某个生产井符合平面径向渗流的条件。各小层相关参数如下：

Re=300 m

K0=83×10-3μm2

K1=41×10-3μm2

φ0=0.160

φ1=0.151

μw1=μw0=0.5 mPa·s

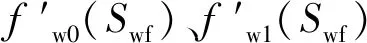
根据以上参数，由式(8)计算得m=0.482 9。再由式(5)，推导出式(10)：

(10)

式(10)可反映出，对两小层同时开始注水驱油后，在同一时刻其水驱前缘位置与注采压差之间的函数关系。

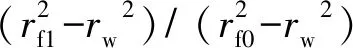
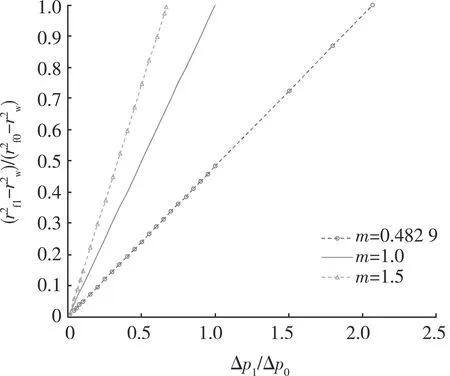
图与Δp1/Δp0关系曲线

m对非均质性的影响，分以下两种情况：

(1) 当m=1.0，即︱m-1︱=0时，两小层的储渗参数相等，在Δp1Δp0=1.0的情况下两者的水驱前缘同时到达采出端(rw)，不会发现生层间突进。

(2) 当m≠1.0，即︱m-1︱≠0时，随着︱m-1︱值增大，在同一Δp1Δp0下，与前一种情况的差距增大，即储渗纵向非均质程度趋于严重。

由此，可以定义两小层的储渗纵向非均质系数：

ξ=|m-1.0|

(11)

式中：ξ—— 储渗纵向非均质系数，无因次。ξ值越大，则表示储渗纵向非均质程度越严重。

已知“0”号小层的注采压差，即Δp0=9 MPa，则由式(6)可计算出“1”号小层在不同注采压差下(Δp1分别为2.07Δp0、1.00Δp0、0.50 Δp0、3.00 Δp0、4.00 Δp0)vrf与rf的关系(见图3)。

为了进一步描述层间注采压差的优化情况，结合式(9)，分以下3种情况进行讨论：

(1) 当Δp1Δp0=2.07，即m·(Δp1Δp0)=1.0时，“1”号小层与“0”号小层的水驱前缘移动速率处处相等，两小层水驱前缘同时到达采出端(rw)。 在这种情况下不发生层间突进，注采压差达到最优。

(2) 当Δp1Δp0<2.07，即m·(Δp1Δp0)<1.0时，“0”号小层的水驱前缘移动速率处处大于“1”号小层，“0”号小层的水驱前缘先到达采出端(rw)，“0”号小层发生层间突进。

(3) 当Δp1Δp0>2.07，即m·(Δp1Δp0)>1.0时，“1”号小层的水驱前缘移动速率处处大于“0”号层，“1”号小层的水驱前缘先到达采出端(rw)，“1”号小层发生层间突进。

现场实际情况是，两小层注采压差均为9 MPa，也就是Δp1Δp0=1.0。当“0”号层在采出端已经见到注入水后，“1”号层的水驱前缘rf1=215.7 m，发生了层间突进现象。因为此实例中两小层之间的渗透率差异大，而其他参数差异不大，所以，层间非均质性主要体现在渗透率的级差上。“0”号小层水驱前缘从注入端到达采出端的实际时间为270 d，而用式(5)计算的见水时间为288.1 d ，相对误差仅为6.28%；“1”号小层水驱前缘从注入端到达采出端的实际时间为552 d，而用式(5)计算的见水时间为596.6 d，相对误差仅为7.48%。

由图3也可以看出，只有在Δp1Δp0=2.07，即m·(p1Δp0)=1.0的条件下，两小层在不同井距处的渗流速率才会相等，不会发生层间突进现象，注采压差才达到了最优化。

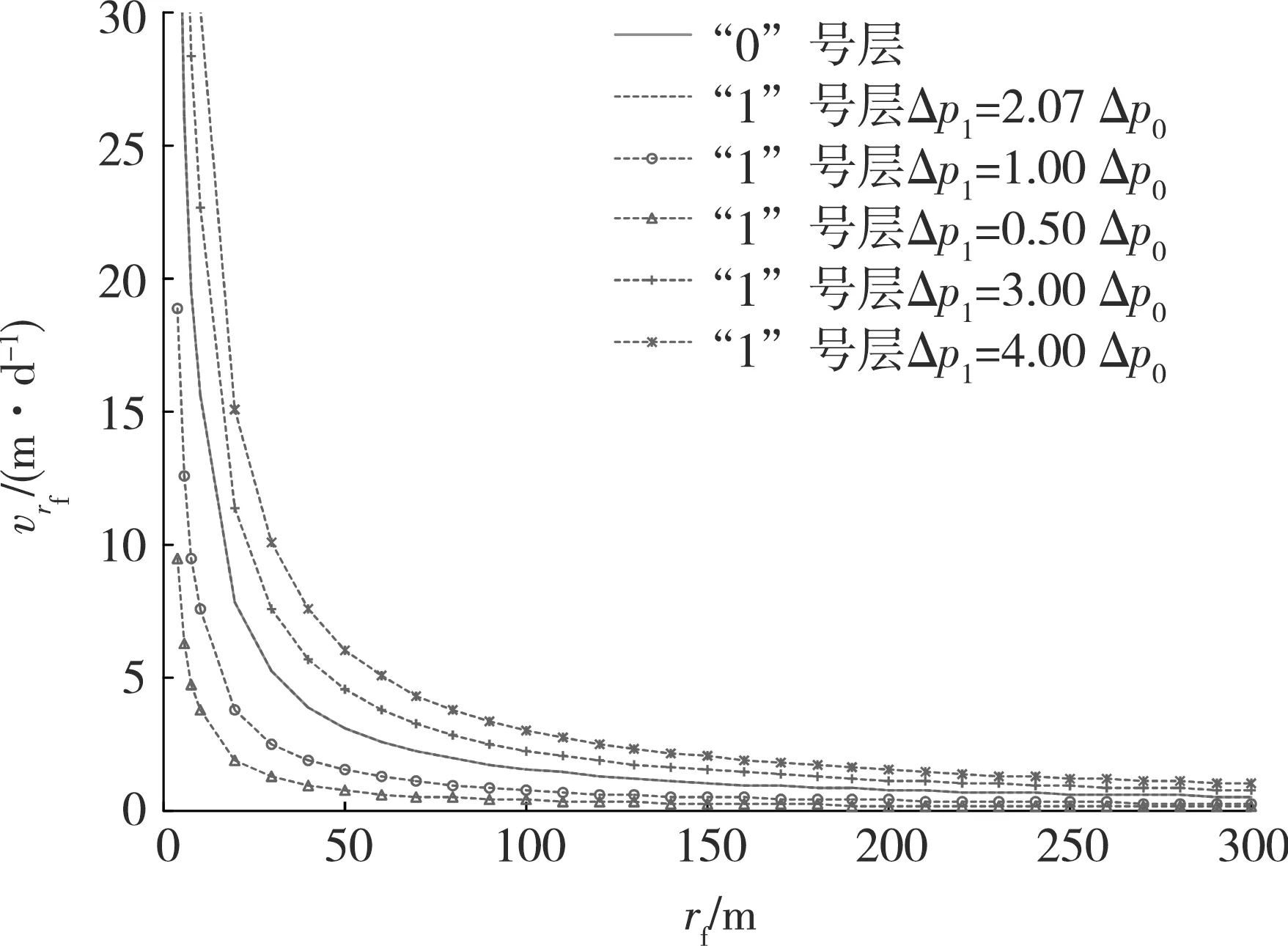
图3 vrf与rf关系曲线

3 结 论

基于水驱油藏基本渗流理论，运用数学解析法，建立了满足平面径向渗流条件下的两层层间注采压差优化模型，经实践检验，该模型是合理可行的。定义了储层的储渗纵向非均质系数ξ，ξ越大，则储层的储渗纵向非均质程度越严重。调整分层注采压差是解决层间矛盾的有效方法，最优分层注采压差应满足关系式：m·(Δp1Δp0)=1.0。