基于萤火虫算法优化神经网络的风电功率预测

谭 剑

中国能源建设集团华中电力试验研究院有限公司 湖南 长沙 410000

1 引言

由于传统能源的日渐减少,风力发电等清洁新能源越来越引起社会的重视。我国风力资源十分丰富,有效利用将大大改善我国的用电压力。然而,风力受多种因素影响,具有随机性与间歇性等特点,加大了风电并网的难度。利用已有的风电数据对其功率精确预测将有效帮助电力部门有针对性做出决策,保证居民生活、工业生产等多方面的用电需求,在保证电力质量的前提下,降低电网的运行成本[1－2]。

目前,国内外学者紧跟时代步伐,在风电功率预测方面做出了大量研究,常见的方法有小波分析、支持向量机、极限学习机、时间序列法等。文献[3]采用小波变换对原始变量进行分解,并结合神经网络进行短期风电功率预测,有效提高了预测精度,但是小波变换公式复杂,所需工作量较大。文献[4]建立多输入单输出的BP神经网络模型,能够较好地用于预测风电机组的输出功率,但是BP神经网络预测精度仍有待提高,且容易陷入局部最优。文献[5]基于支持向量机理论,建立了4h风电功率预测模型,为短期功率预测提供了一种方法,但支持向量机预测精度不足,误差较高。

本文针对以上问题,选取风速、温度、电流等影响功率的因素,建立一种基于萤火虫算法(Firefly Algorithm,FA)优化BP神经网络的预测模型,并与ELM、BP神经网络模型预测性能进行对比。结果表明,本文提出的方法能够降低预测误差,提高预测准确度,在超短期与短期风电功率预测方面效果显著,应用前景显著。

2 理论建模分析

2.1 BP神经网络 BP神经网络]作为一种能够通过不断学习更新权重和阈值的反馈网络,理论上能够无限逼近任何函数,已经在许多领域得到了很好的应用。BP神经网络分为正向传递与反向传递两个过程,通过梯度下降法不断减小误差值,其基本结构包括输入层、隐含层与输出层,

2.2 萤火虫算法 萤火虫算法是一种模拟萤火虫群聚活动寻找种群最优而提出的启发式算法。每只萤火虫均有一个初始发光强度,随着时间的推移,发光弱的个体会向发光强的个体移动,改变萤火虫的位置,完成迭代过程,具体规则如下：

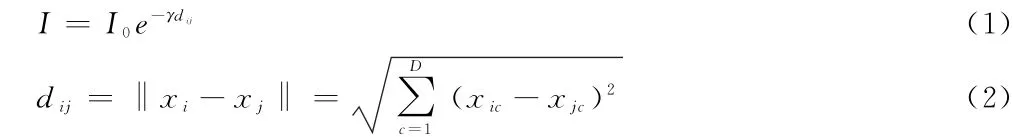
式中,I为萤火虫个体的相对荧光亮度；I0为萤火虫个体当前位置的亮度,随着适应度函数的更新而变化；γ为发光强度吸收系数；d ij为两个体间的距离；D为萤火虫所处空间的维度；x ic与x jc分别为第i只萤火虫与第j只萤火虫在空间中的第c个分量。

不同发光强度的萤火虫之间通过吸引来改变位置,萤火虫之间的吸引度定义为

式中,βij为第i只萤火虫与第j只萤火虫之间的吸引度值,β0为初始吸引度。

迭代过程中,每只萤火虫位置更新规则为

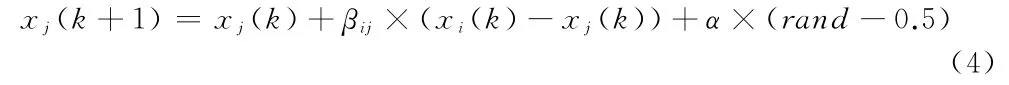
式中,x i与x j分别为第i只萤火虫与第j只萤火虫的空间位置,k为迭代次数,α为步长因子,rand为[0,1]上服从均匀分布的随机因子。

当满足全局最优或者达到最大迭代次数时,寻优结束。萤火虫算法原理清晰易懂,参数数量较少,可用来改善原始BP神经网络的预测性能。

2.3 萤火虫算法优化BP神经网络 本文运用FA算法优化BP神经网络,构建FA－BP预测模型,改善风电功率预测准确度。

3 实验验证与分析

3.1 数据预处理 风电是一个多参数且非线性的复杂能源系统,影响风电性能的各项参数往往具有不同的量纲与数值。如果直接用原始数据作为神经网络的输入,那么将会导致误差的增大,无法提供准确的预测结果。基于此,需要首先进行归一化处理。

本文采用“mapminmax”公式对原始数据进行归一化处理,使新数据处于[－1,1]范围内,消除各参数之间的差异性,如式(5)所示：

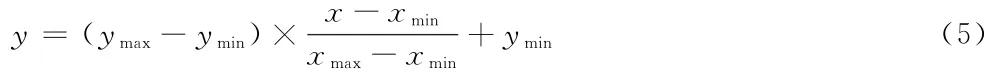
式中,y为归一化后的无量纲新数据,ymax＝1,ymin＝－1,x为原数据,xmax与xmin分别为原数据中的最大值与最小值。

3.2 效果评价标准 为了突出所构建模型的预测性能,本文分别采用均方根误差(Root Mean Square Error,RMSE)与平均绝对误差(Mean Absolute Error,MAE)来反映预测效果,计算公式如下：

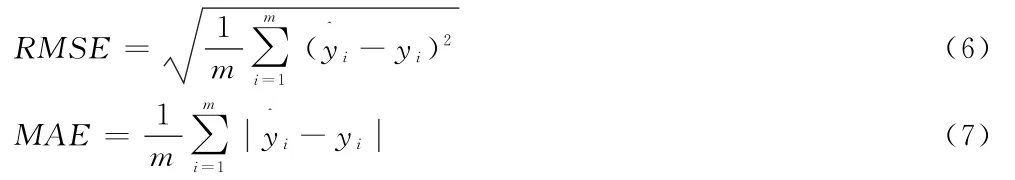
式中,y i为风电功率的实际值,为风电功率的预测值,i＝1,2,…,m。

3.3 参数设置与实验结果 为了验证本文所提出的FA－BP方法在风电功率预测方面的优越性,选取国内某风电场2018年5月1日～2018年6月7日采集的数据作为样本来源,每隔30min采样一次。其中,2018年5月1日～5月31日的数据为训练样本,共1488组。2018年6月1日数据为测试样本1,共48组,预测一天的功率；2018年6月1日～6月7日数据为测试样本2,共336组,预测一周的功率。

根据选择的数据,风速、温度、电流为模型输入,风电功率为模型输出。构建3层网络结构,输入层设置为3,隐含层为10,输出层为1,学习率为0.1,全局训练目标为0.00001。萤火虫种群数量为20,迭代次数为100,步长因子为0.5,初试吸引度为0.2,发光强度吸收系数为1。

(1)2018年6月1日预测结果

图3(a)－(d)是ELM、BP以及FA－BP模型在2018年6月1日的风电功率预测结果图与对比图。从图中可以直观看出,与其余两种模型相比,FA－BP模型能够较好地预测风电功率,误差更小,精度更高。

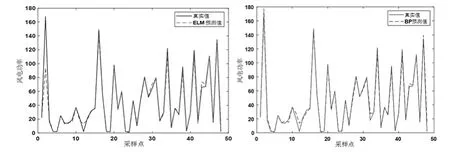
(a)ELM风电功率预测结果(b)BP神经网络风电功率预测结果

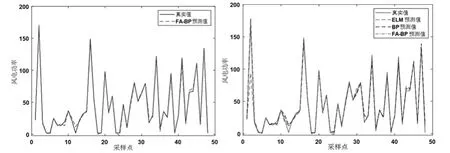
(c)FA－BP风电功率预测结果(d)三种模型风电功率预测结果图3 三种模型一日风电功率预测结果

表1为三种模型一日风电功率预测结果,从表中可以看出,FA－BP模型的RMSE误差相对ELM与BP分别降低了7.7862%与0.7833%,MAE误差分别降低了1.4331%与0.3843%。综合分析,FA－BP能够有效降低预测的误差,提高风电功率预测的精度。

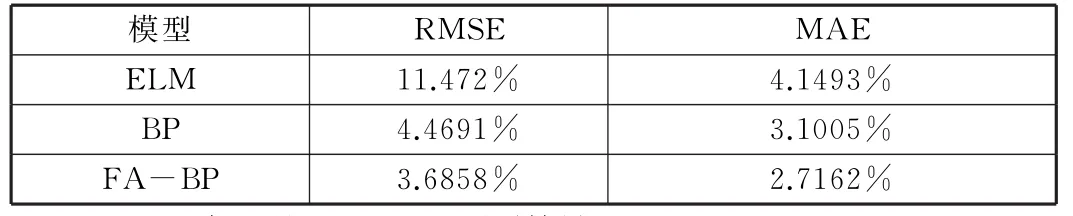
表1 三种模型一日预测结果对比

(2)2018年6月1日～7日预测结果

图4(a)－(d)是ELM、BP神经网络以及FA－BP模型在2018年6月1日～7日的风电功率预测结果图与对比图。从图中可以直观看出,与其余两种模型相比,FA－BP模型能够较好地预测一周的风电功率,误差更小,精度更高,为电力调度提供了一种有效预测手段。

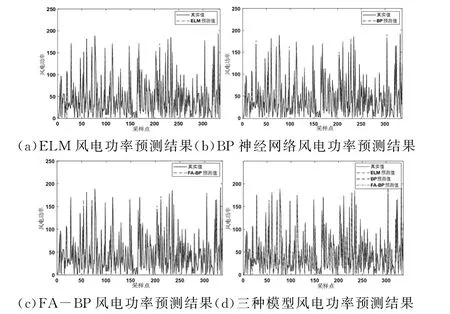
图4 三种模型一周风电功率预测结果

表2为三种模型一周风电功率预测结果,从表中可以看出,FA－BP模型的RMSE误差相对ELM与BP分别降低了2.6364%与2.0413%,MAE误差分别降低了0.0946%与0.3112%。综合分析,FA－BP能够有效降低预测的误差,提高风电功率预测的精度。

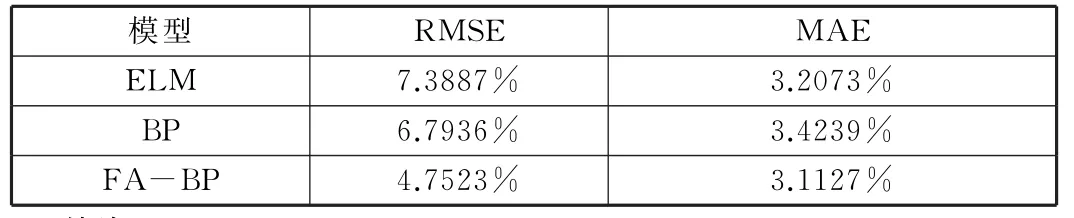
表2 三种模型一周预测结果对比

4 结论

风电功率预测是电力调度部门合理分配电能资源的一种有效手段,合理的风电功率预测将提高调度的效率,满足生产生活等各方面的需求。本文选取风速、电流、温度作为模型输入,通过FA－BP模型进行风电功率预测,得出如下结论：

(1)FA算法能够有效优化BP神经网络,并用于风电功率的预测。与原始BP神经网络、ELM性能相比,FA－BP模型能够显著降低预测误差,提高预测精度。

(2)运用FA－BP神经网络模型进行风电功率预测,一日预测的RMSE误差为3.6858%,MAE误差为2.7162%,误差比另外两种模型明显降低,可以作为电力调度部门日调度的依据。

(3)FA－BP模型进行一周风电功率预测,RMSE误差为4.7523%,MAE误差为3.1127%。虽然误差比一日预测的结果高,但结果仍然可以接受,并且比另两种模型预测精度更高。

(4)本文提出的FA－BP模型,无论是一日预测还是一周预测,均取得了满意的预测结果,为风电功率预测提供了一种新的方法,具有一定的实际应用价值。