核燃料棒包壳腐蚀对格架磨蚀的影响研究

(中国核动力研究设计院 核反应堆系统设计技术重点实验室,四川 成都 610213)

压水堆中,燃料棒在高速流动的冷却剂作用下会发生微幅振动,引起定位格架的弹簧/刚凸与燃料棒包壳之间发生格架微动磨蚀,微动磨蚀是燃料棒破损的重要原因之一。燃料组件安全分析主要通过堆外振动试验和耐久性试验[1],以及对比具有相似结构的燃料组件运行经验来说明格架磨蚀不会超过设计准则。

国产燃料组件研制了新材料,设计了新结构,难以借鉴成熟的商用燃料组件运行经验,除堆外试验之外还需要研究适用的微动磨蚀计算方法。燃料棒的随机振动响应非常复杂，难以模拟,现有的专用磨蚀计算程序将不确定量取上限值或采用蒙特卡罗方法进行保守计算[2],将磨蚀过程处理为平均过程,例如法国的VIBUS和西屋公司的VIBAMP、VITRAN程序。

近几年的微动磨蚀研究中逐渐揭露出磨蚀过程的变化性,由于包壳腐蚀作用导致磨蚀过程具有随机性,并且氧化产生的氧化膜对磨蚀有抑制作用[3-4]。

反应堆内快中子辐照使水辐解产生氧,部分氧与金属锆反应产生氧化锆。由于寿期初格架夹持力足够大,燃料棒与弹簧/刚凸不会发生相对位移,包壳表面会生成氧化膜；夹持力松弛,燃料棒与弹簧/刚凸开始相对运动后,格架会首先对氧化膜进行磨蚀。因此,为了准确模拟磨蚀过程,提高磨蚀计算的准确性,需要研究包壳腐蚀过程以及腐蚀产生的氧化膜对磨蚀过程的影响。

本文根据腐蚀包络模型和ARCHARD磨蚀计算公式建立并完善了堆内磨蚀的多时期磨蚀模型,分析了包壳腐蚀对磨蚀系数测量试验的影响,然后结合振型叠加原理,以保守的燃料棒振动响应结果为输入,计算并分析了不同氧化膜结构对磨蚀计算结果的影响。

1 包壳腐蚀

氧化锆有三种同素异构体,分别为单斜相、四方相和立方相,受温度和压应力影响,三种结构之间可以互相转换[5]。在压水堆冷却剂温度下,稳定的是单斜相氧化锆。但金属锆变成氧化锆时,体积会膨胀,二者体积比为1∶1.56,在金属基体的约束下,氧化膜内部会产生压应力[6],在该压应力的作用下,氧化膜的主要成分为四方相氧化锆。

四方相致密,对锆合金金属基层有一定的保护作用,而单斜晶的密度和硬度均小于四方晶。随致密层氧化膜厚度的增加,氧难以扩散到锆金属层,氧化速率(氧化膜厚度增加速率)逐渐降低。当氧化膜厚度增加到一定厚度(转折厚度)时,压应力松弛,外层的四方相开始转化为单斜相。

氧化转折之后,锆金属继续被氧化,氧化膜中的裂纹和孔隙聚集,导致氧化膜外层转变为疏松层,而致密层厚度略微减小。因此氧化转折后的氧化膜是外层疏松和内层致密的双层结构,由于转折后的腐蚀速度几乎是线性,说明起保护作用的致密层的厚度几乎不变。

根据N36锆合金包壳池边检查结果,N36氧化行为满足典型的阿累尼乌斯方程[7],即氧化转折前满足的立方动力学方程(1)和氧化转折后满足的线性动力学方程(2)。

(1)

(2)

因此,可以将N36包壳氧化膜的厚度增长规律描述为(如图1所示)：致密层氧化膜从0开始逐渐增加(内层四方相,外表面单斜相),增加速度越来越慢；当氧化膜厚度超过转折厚度后,外层疏松并且厚度快速线性增加,内层致密层并且厚度保持略小于转折厚度。

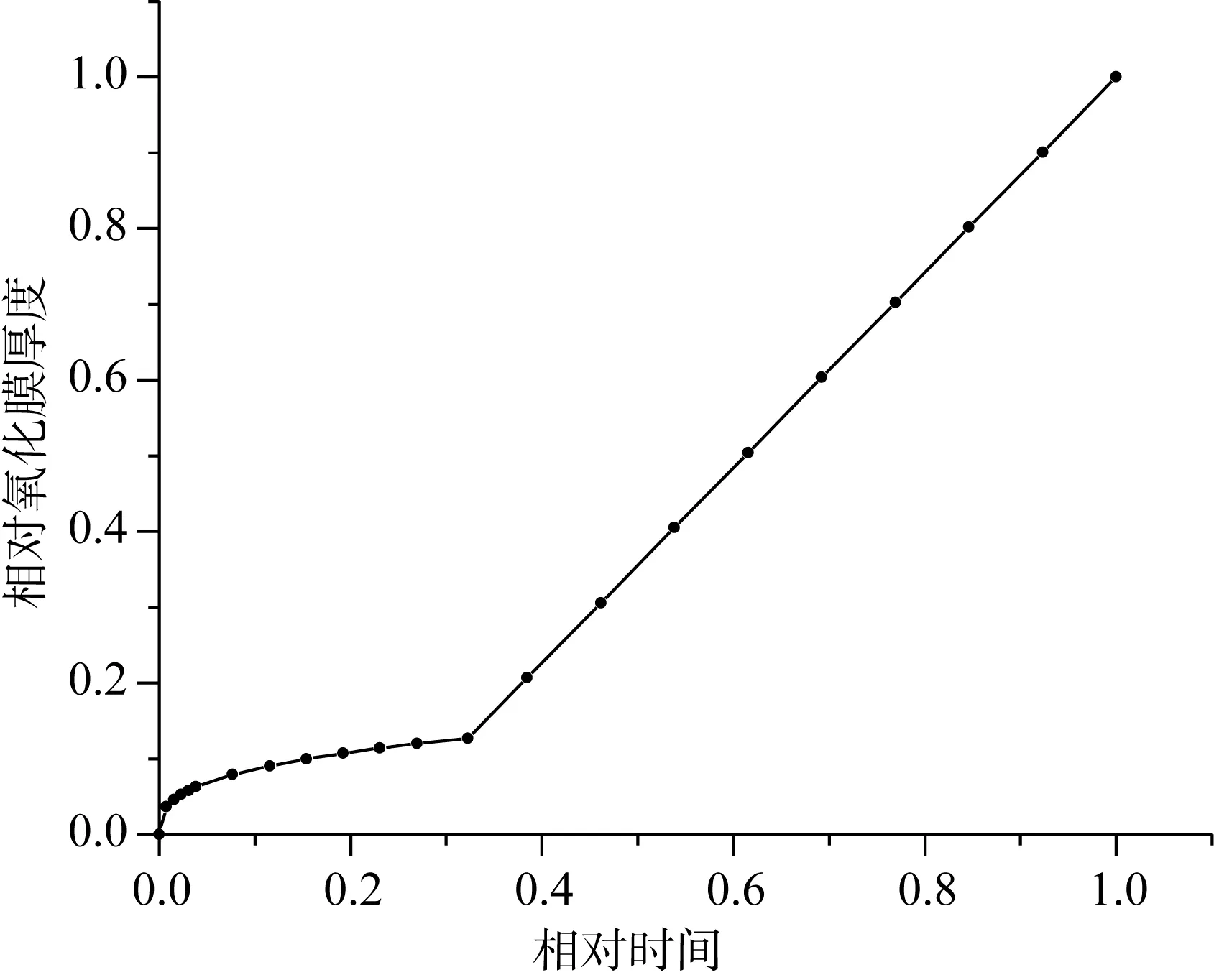
图1 包壳氧化包络模型示意图Fig.1 The schematic of cladding oxidation envelope model

2 磨蚀模型

2.1 磨蚀阈值

美国橡树岭国家实验室针对预氧化处理包壳的堆外磨蚀试验提出了预磨蚀期、预氧化膜磨蚀期和金属层磨蚀期的多时期磨蚀模型。

反应堆内,燃料棒振动时对弹簧/刚凸产生摩擦力,寿期初夹持力较大,弹簧/刚凸在静摩擦力作用下与燃料棒一起振动,不发生相对运动。快中子辐照作用下格架夹持力逐渐减小,燃料棒对弹簧/刚凸的摩擦力不足以克服弹簧/刚凸的回复力时,开始发生相对运动,产生格架磨蚀(如图2所示)。

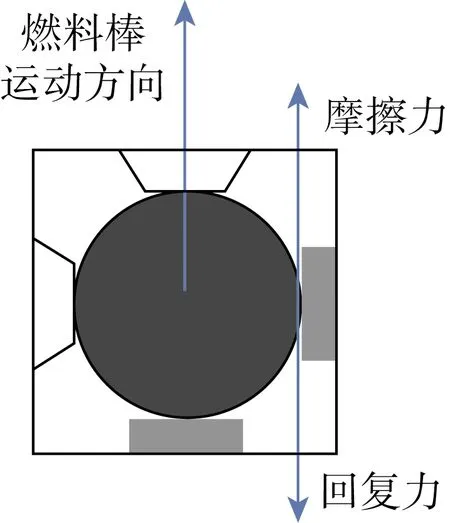
图2 燃料棒与弹簧/刚凸相对运动关系Fig.2 The relationship of relative motion between fuel rod and spring/dimple

可以根据弹簧/刚凸的切向刚度Ktb,燃料棒与弹簧/刚凸的摩擦系数μ和燃料棒的运动幅度A计算发生相对运动时的最小夹持力F0。

F0=AKtb/μ

(3)

即当格架夹持力小于磨蚀阈值F0时,燃料棒与弹簧/刚凸间会发生相对运动,造成格架磨蚀。在没有磨蚀发生的这段时期称之为预磨蚀期,燃料棒包壳表面同时在不断腐蚀产生氧化膜。堆外的高温高压磨蚀试验,在试验开始前的升温保温过程中,包壳表面也会发生轻微的氧化,同样也可以将这段时期称为预磨蚀期。

弹簧/刚凸与包壳为线接触或点接触时,包壳附近的氧浓度与跨间接近,所以弹簧/刚凸接触处的氧化膜生成速率与跨间接近,假设为均匀环形分布。

预磨蚀期的长短与格架夹持力、弹簧/刚凸切向刚度、包壳与弹簧/刚凸之间的摩擦系数,中子注量和燃料棒振幅相关。初始夹持力很小时,可能出现没有预磨蚀期直接发生相对运动的情况。初始夹持力大,同时中子注量率低,夹持力松弛慢,始终大于磨蚀阈值,燃料棒与弹簧/刚凸在整个寿期内不会发生相对运动(例如位于活性区外的上端部格架)。所以不同位置不同初始条件的格架处,弹簧/刚凸与包壳开始发生相对运动时,包壳表面氧化程度各不相同。

2.2 多时期磨蚀模型

磨蚀开始时,首先对氧化膜进行磨蚀,氧化膜又分为疏松层和致密层。当氧化膜穿透后开始接触到金属层,进入过渡阶段。当弹簧/刚凸主要与金属基层接触时,则进入金属基层磨蚀期。因此可以将磨蚀过程划分为预磨蚀期、氧化膜磨蚀期、过渡期和金属基层磨蚀期等四个时期(如图3所示)。

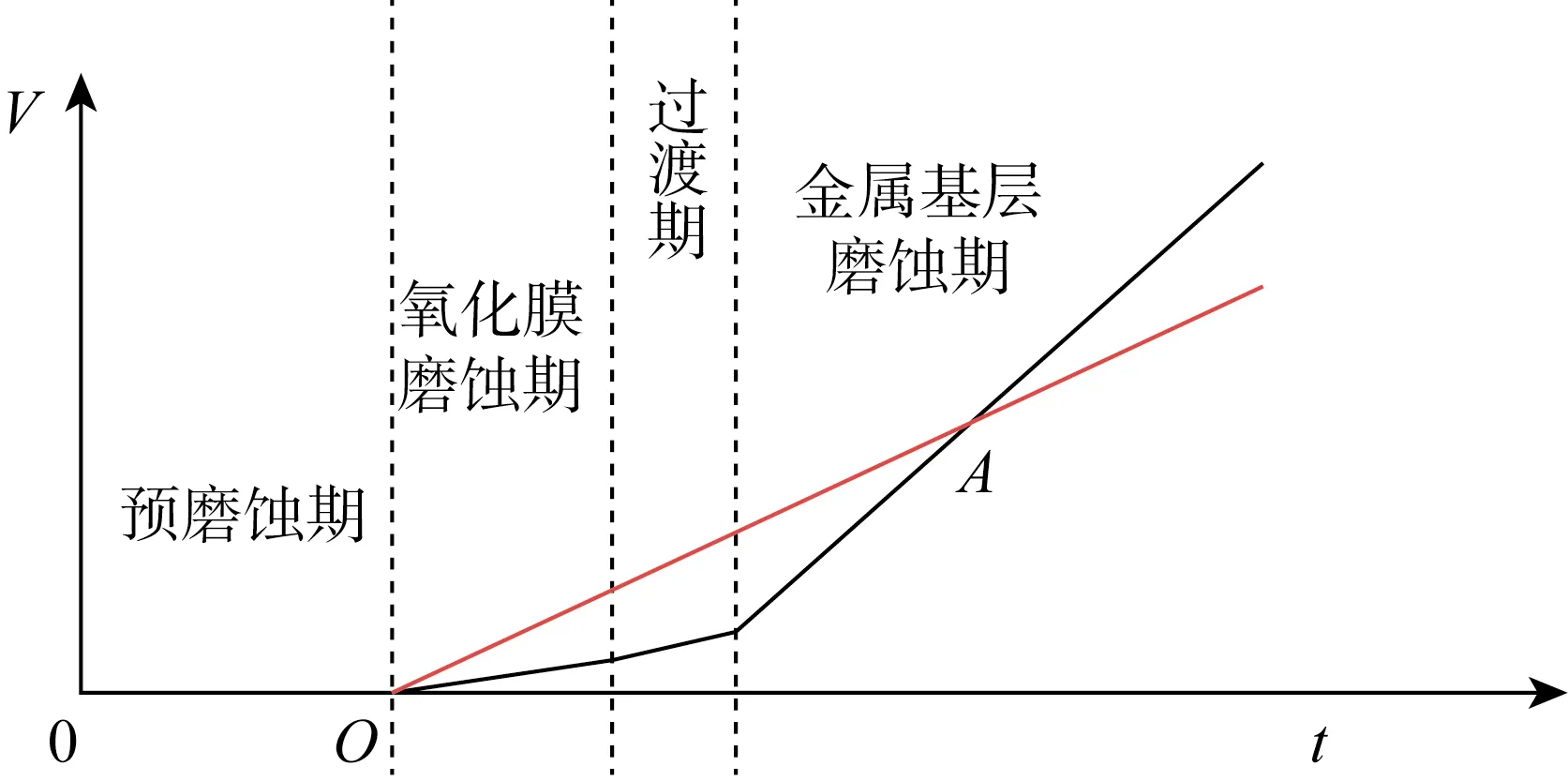
图3 多时期磨蚀模型示意图Fig.3 The schematic of a multi-stage wear model

进入金属基层磨蚀期后,在腐蚀作用下包壳表面会不断生成四方相氧化锆,然后变为单斜相被磨蚀掉,即腐蚀过程与磨蚀相结合,体现到磨蚀系数中。

在耐久性试验或高温高压磨蚀试验中,磨蚀过程同样符合多时期磨蚀模型,但在数据处理时往往将磨蚀系数看作平均值(如图3中线段AO的斜率),然后将磨蚀系数或磨蚀结果进行外推计算。根据多时期磨蚀模型,平均磨蚀系数比金属基层磨蚀系数小,随着磨蚀的不断发展,会导致预测的磨蚀结果比实际情况偏小。为了得到实际的磨蚀发展曲线,可以进行多次不同时间的磨蚀试验,得到位于不同时期内的磨蚀结果,模拟多时期磨蚀过程,从而准确外推到寿期末的格架磨蚀情况。

美国橡树岭国家实验室分别对预氧化处理和无氧化锆合金包壳管在常压水中进行了磨蚀试验,结果表明金属层的磨蚀系数约为氧化膜磨蚀系数的50～200倍[4]；并且法国AFA3G组件M5合金的磨蚀系数(高温高压水中)只有该试验中氧化膜磨蚀系数的2倍。这可能是由于未考虑多时期磨蚀过程导致平均磨蚀系数远小于金属层磨蚀系数,而略小于氧化膜磨蚀系数,也说明了高温高压环境下腐蚀过程不断产生的四方相氧化锆对磨蚀有抑制作用。

2.3 磨蚀系数

根据平面接触假设和ARCHARD磨蚀体积计算公式求各个阶段的等效磨蚀系数。预磨蚀时期较短,只有致密层氧化膜时,过渡层上有两种成分。预磨蚀时期较长,磨蚀开始时包壳表面有疏松氧化膜和致密氧化膜(如图4所示),出现两种情况的过渡层。按平面假定和磨蚀体积计算公式可以计算出对应的等效磨蚀系数。通过简单的几何分析,可以得到不同区域的面积A1、A2和A3。

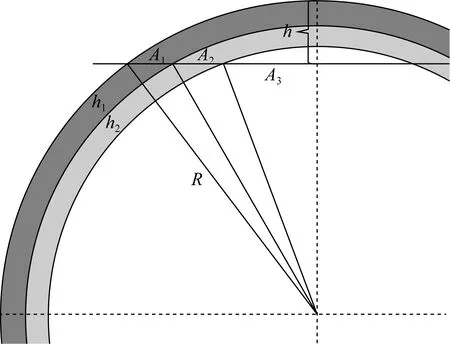
图4 过渡层面积比例计算示意图Fig.4 The schematic of transition layer area proportion calculation

假设消耗在三种表面上的磨蚀功分别为W1、W2和W3,根据ARCHARD磨蚀体积计算公式：

ΔVi=κiWi(i=1,2,3)

(4)

总磨蚀体积为：

ΔV=κW=κ1W1+κ2W2+κ3W3

(5)

等效磨蚀系数为：

κ=(κ1W1+κ2W2+κ3W3)/W

(6)

根据磨蚀面始终保持平面的假定：

ΔV1/ΔV2=A1/A2

(7)

ΔV1/ΔV3=A1/A3

(8)

得到等效磨蚀系数与疏松层、致密层和锆合金层的磨蚀系数与面积的关系式：

(9)

当没有接触到金属层时A3=0,κ3=0。即

(10)

由预磨蚀期长度和包络氧化模型计算出对应格架位置处不同初始夹持力的氧化膜厚度后,再由磨蚀系数随磨蚀深度的关系式,结合多时期磨蚀模型可以计算得到考虑氧化包络模型后的磨蚀体积和平面接触假设下的最大磨蚀深度。

3 计算结果及分析

以CF3内条带栅元对应的燃料棒振动响应结果作为输入,根据ARCHARD公式分别计算不同格架处、各种初始夹持力对应的磨蚀深度,计算结果如图5所示。

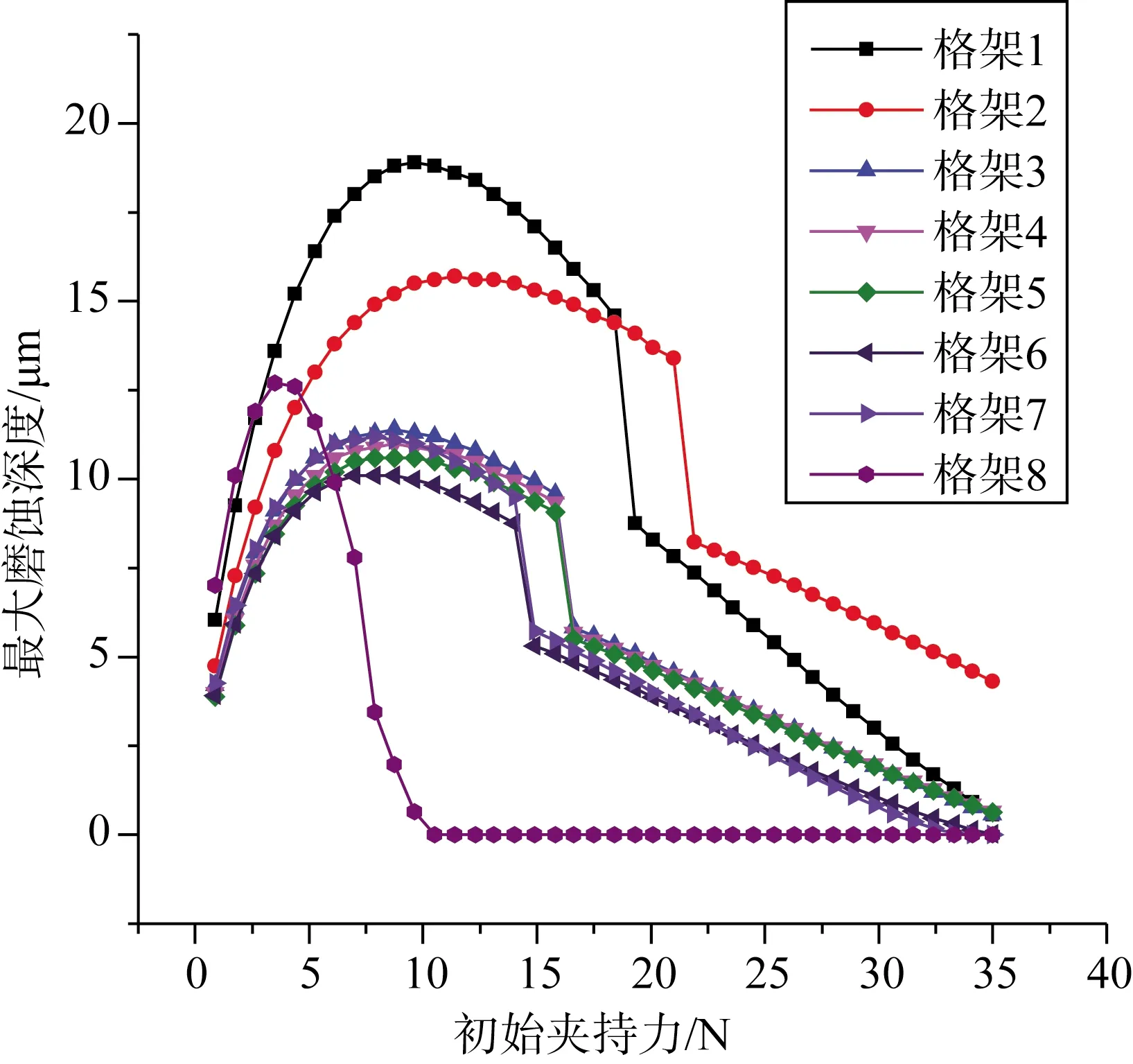
图5 磨蚀计算结果Fig.5 The results of wear calculation

氧化膜增长模型与预磨蚀期长度相关,预磨蚀期长短决定了磨蚀开始时已经形成的氧化膜厚度及成分,而预磨蚀期长度由初始夹持力直接决定。预磨蚀期长度随初始夹持力增加而增加,氧化膜厚度增大,对包壳表面进行保护,则磨蚀量越小。当初始夹持力超过一定值时,弹簧/刚凸甚至不会磨损到金属基体,磨蚀深度显著降低(如图5中曲线的突然下降)。

当疏松层氧化膜和致密层氧化膜分别取不同磨蚀系数时,对3号格架初始夹持力分别为10.5 N和17.5 N的情况进行磨蚀计算,结果如图6所示。致密层磨蚀系数取为0.2×10-15Pa-1,而疏松层磨蚀系数按金属层磨蚀系数百分比依次增加,初始夹持力为10.5 N时,最大磨蚀深度不变,而初始夹持力为17.5 N时,最大磨蚀深度成比例增加。初始夹持力较小,预磨蚀期较短,形成的氧化膜厚度较薄,甚至没有疏松层产生,因而疏松层磨蚀系数对最终磨蚀计算结果无影响；初始夹持力较大,预磨蚀期较长,形成较厚的氧化膜,疏松层对磨蚀深度的影响占主导地位。

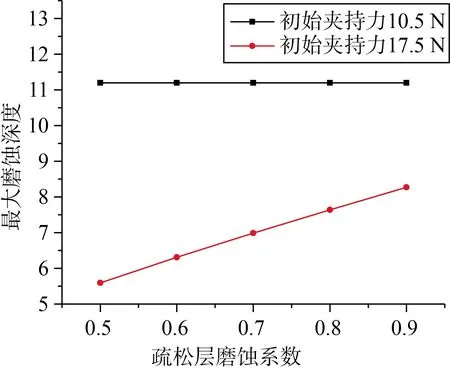
图6 磨蚀深度随疏松层磨蚀系数的变化Fig.6 Variation of the wear depth with increasing wear coefficient of loose oxide

之后保持疏松层磨蚀系数不变,致密层磨蚀系数从0.1×10-15Pa-1逐渐增加到0.5×10-15Pa-1,对应10.5 N和17.5 N的最大磨蚀深度计算结果完全不变。这是由于致密层较薄,在整个磨蚀时期内贡献较小,对最终磨蚀计算结果影响很小。

所以致密层由于始终很薄,对整个磨蚀计算结果影响很小。对于疏松层,当初始夹持力较小时,预磨蚀期较短,氧化膜的影响不显著,计算结果与无氧化膜接近；初始夹持力足够大时,预磨蚀期较长,氧化膜较厚,磨蚀深度明显减小。

格架1和格架2的振动响应幅度最大(见表1),格架8位于活性区外,格架1位于活性区底部,中子注量比其它格架处小。所以振幅越大,中子注量率越大,包壳腐蚀使磨蚀明显减小时对应的初始夹持力越大。

表1 全部格架处的燃料棒振动响应幅度Table 1 The amplitude of fuel rodvibration response at all grids 单位：μm

4 结 论

预磨蚀期内,由于包壳腐蚀产生的氧化膜会使磨蚀试验中磨蚀体积减小,导致平均磨蚀系数偏小,直接采用平均磨蚀系数进行磨蚀预测不够保守,需要结合多时期磨蚀模型分析测量多个数据点模拟实际磨蚀过程。

致密层氧化膜由于厚度较小,总体对磨蚀计算结果影响较小。格架初始夹持力较小时,预磨蚀期短,没有形成足够厚的氧化膜,腐蚀作用对磨蚀的影响只体现在后续微观磨蚀过程中；格架初始夹持力大时,预磨蚀期长,产生了较厚的氧化膜,最大磨蚀深度随疏松层氧化膜磨蚀系数增大而增加。燃料棒振幅越大,中子注量率越大,包壳腐蚀使磨蚀明显减小时对应的格架初始夹持力越大。