基于PSO的船体动态变形模型参数在线辨识

于东康，杨功流，谢祖辉

（北京航空航天大学仪器科学与光电工程学院，北京100191）

0 引言

现代化大型舰船通常装备有雷达、光学观瞄设备、跟踪测量设备、武器发射设备等［1］。这些设备正常工作的前提，是其拥有统一的时空基准。一般而言，时间基准通常为GPS时钟或船上当地时钟信号，而空间基准则是船舶在陆地建造期间将各设备的空间姿态坐标进行高精度匹配而建立起来的［2］。

由于舰船并非绝对刚体，在实际航行过程中难免受日晒、海浪冲击等外力作用而产生角形变，这使得舰上各设备失去了统一的空间基准，影响了其信息共享与协同作战的能力。学者Mochalov等人所做的研究表明，舰船的静态变形角最大可达1°～1.5°，其动态挠曲变形角可达数角分。为保证设备的正常工作，需对船体形变角进行精确测量并进行补偿［3⁃4］。

近年来，各国不断加深在船体变形测量领域的研究，并相继出现了一系列的测量方法。其中，美国先后提出激光跟踪法、应变测量法等方法；俄罗斯Mochalov团队开展了基于激光陀螺组合体（LGU）的形变角测量方法研究。国内方面，秦石乔教授提出了自准直平行光管法；长春光机所采用大钢管法研制了一套光学形变监测系统，并进行了实船验证；学者郑佳兴针对基于姿态匹配的变形角解算方法，进行了细致的研究。

相较于传统的光学测量法、应变测量法等，利用多套捷联惯导系统、基于惯性量匹配的船体变形角测量方法拥有测量精度高、易于实现等优点，是时下研究的热点，而基于角速度匹配［5］、惯性姿态匹配［6］等的多种匹配算法也陆续出现。要得到高精度的测量结果，必须解决的一项难点就是动态挠曲变形模型参数的辨识。对此，传统的做法是通过处理一段变形测量的历史数据来解出相应的参数，即所谓的 “先验数据分析法”。但实际上，受环境影响，动态模型参数是实时变化的，由先验数据解出的既定参数无法满足需要。文献［7］提出了基于交互式多模型滤波的变形测量方案，通过自适应估计的方法解决了参数变化的问题。文献［8］提出，在2套INS的角增量输出差值中包含动态挠曲角信息，并推导得到了角增量差值的自相关函数值，其为指数衰减正弦信号（EDS）形式，最终利用基于后向预测及奇异值截断的方法（T⁃K法）解出了动态模型的参数，具有较高的精度。

受文献［8］启发，本文利用2套INS的角增量差值自相关函数为EDS形式建立了模型，采用粒子群算法进行动态挠曲变形模型参数的在线估计，并将所估参数应用于基于角速度匹配的Kalman滤波器中，进行变形角的估计。上述方法在仿真实验中取得了良好的求参效果，且在不同程度噪声的干扰下均获得了较高的求参精度。结合该参数辨识方法的船体变形角估计误差能够控制在10″左右，满足了工程应用的需要。

1 角速度匹配法及动态挠曲角模型

1.1 角速度匹配方程

光纤陀螺捷联惯导系统（FOG SINS）主要由3只光纤陀螺与3只加速度计组成，它们分别安装在由精密机械结构支撑的3个正交面上。光纤陀螺能够实时敏感载体绕3个正交轴方向的旋转角速度。

假定2套INS分别安装在舰艇的相应位置，如图1所示。其中，INS1坐标系oxyz与船体坐标系（b 系）取齐，INS2 坐标系 ox′y′z′与舰载设备坐标系（s系）取齐。

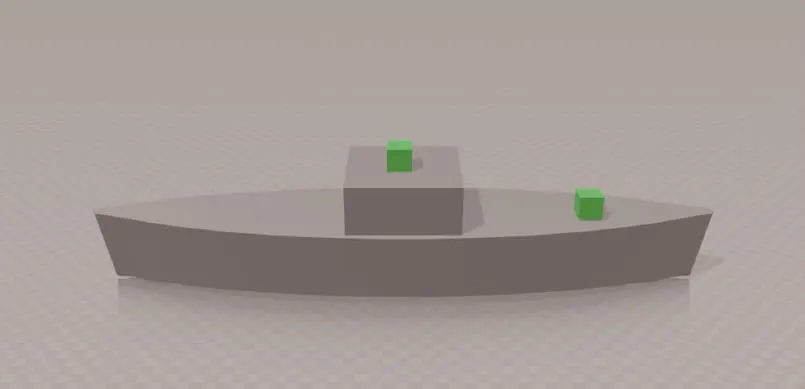
图1 INS安装坐标示意图Fig.1 Installation schematic diagram of INS

总形变角φ由2部分组成，分别为静态形变角Φ和动态形变角θ（t），即有

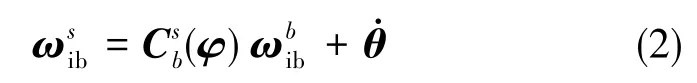
在认为变形角为小角度的前提下，有

在式（4）基础上建立量测方程，以角速度差Δω作为滤波观测量，合理设计线性Kalman滤波器，可以实现对变形角的精确估计。

1.2 动态挠曲角模型

对于短时间的观测而言，舰艇的静态变形角可被视作常值，而动态挠曲变形角来自于外界的动态扰动。更进一步说，其产生的主要原因为舰体在航行过程中所受到的随机风力和流体力的作用，因此它是一种由外界随机力驱动的随机变量，与由白噪声驱动的Markov过程类似。故可以用3个方向独立的二阶Markov过程来建立模型，这种简单的二阶模型适用于大多数应用场合［9］。

动态挠曲变形的自相关函数为

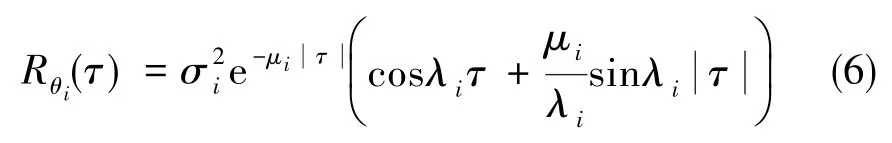
式（6）中，i＝x，y，z分别代表3 个轴向，μi为衰减因子，λi为支配频率，σi为幅度标准差。自相关函数对应的滤波器方程为

变形角的估计精度与动态挠曲模型的3个参数（σ2、μ、λ）的准确性有着直接的关系。由于舰船的航行环境具有多变性和不可预测性的特点，受其影响的动态模型参数也是实时变化的。如何精确辨识出模型参数并将其应用于Kalman滤波，是一项极具挑战性的工作。

1.3 Kalman滤波设计

考虑光纤陀螺漂移的影响，式（4）变化为

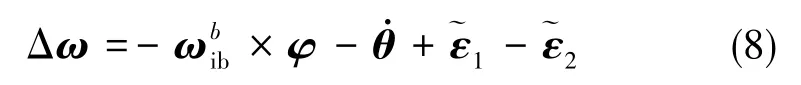
引入陀螺漂移误差模型

式（10）中，κi为随机漂移不规则系数，σ′i为表征漂移不规则程度的均方差。由式（7）、式（10）可给出系统状态方程的矩阵形式

2 基于粒子群算法的参数辨识

2.1 角增量差值自相关函数

将角速度输出在采样时间内进行积分，推导2套INS的角增量匹配关系。记采样周期为t0，考虑第k次采样，对式（4）两边同时积分得到

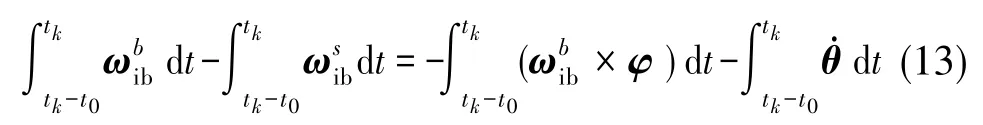
整理后，得到2套INS在第k个采样周期内的角增量匹配方程

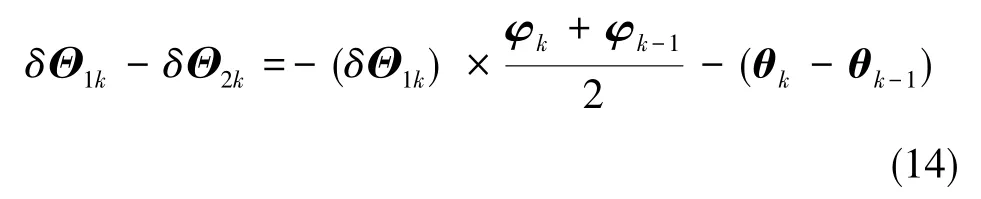
式（14）中，δΘ1k和 δΘ2k分别为INS1和 INS2在单采样周期内的角增量。由φk＝Φ ＋θk，可将其进一步写作

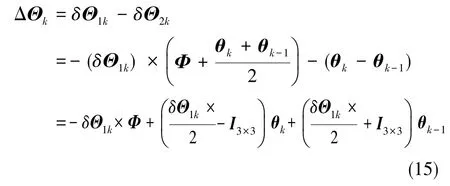
通过所估静态变形角 Φ，可对式（15）中的-δΘ1k×Φ项进行在线补偿，从而将其消掉，即化为

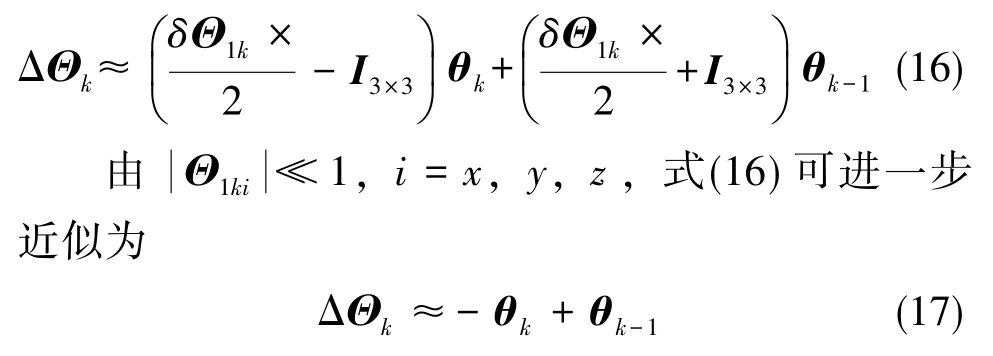
在式（17）的基础上，文献［8］详细推导了 ΔΘ的自相关函数形式，这里直接给出

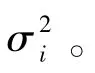
2.2 粒子群算法的参数辨识原理

现在面临的工作是，如何利用式（18）辨识出其中的参数。学者吴伟提出，式（18）的形式为指数衰减正弦波（EDS）叠加的形式，即

式（23）中，信号y（n）由M个EDS信号构成，as为复振幅，w（n）为Gauss白噪声。

基于这点，吴伟选用了一种解EDS信号的方法——T⁃K法，来进行参数的求解。其做法是利用RΔΘ（n）的复共轭数据建立后向预测方程，通过求解预测误差滤波多项式的根得到未知参数。在确定预测误差滤波多项式系数的过程中，还需用到奇异值截断的方法。作为一种纯数学手段，T⁃K法能够得到较高的求参精度，但它的短板是计算量大，对信噪比的门限要求高［10⁃11］。

作为一种智能算法，粒子群算法（PSO）因其全局搜索能力强，被广泛用于参数估计，并表现出了良好的估计性能［12］。PSO算法的基本思路为：首先在n维空间内初始化s个随机粒子（随机解），定义为X＝（X1，X2，…，Xs），并定义其中第i个粒子的位置为Xi，速度为Vi，其个体极值为pi，粒子的群体极值为BestSi。在每次迭代过程中，粒子通过式（24）、式（25）完成位置和速度的更新

式（24）中，w（t）为时变惯性权重，kg＝1，2，…，G，为当前进化代数，r1、r2为分布于区间［0，1］的随机数，c1为局部学习因子，c2为全局学习因子。

利用PSO算法进行动态变形角模型参数的辨识，首先需要明确算法模型。回顾式（18），已知它的形式为指数衰减正弦信号的叠加，借助式（23），可将其进一步简化为

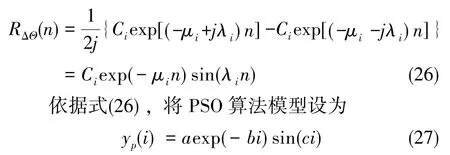
这里，i＝1，2，…，N为数据样本的个数，a、b、c为待辨识参数。以式（27）作为算法模型进行编码，并将适应度函数设为如下形式

式（28）中，y（i）为数据样本真值，J 值越小，越接近真实值，模型参数越准确。PSO算法的具体实现流程如图2所示。

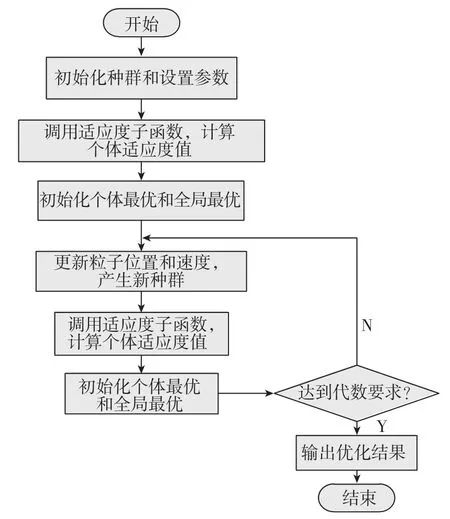
图2 PSO算法流程图Fig.2 Flow chart of PSO

2.3 动态变形模型参数辨识的实现流程

对利用PSO算法进行动态变形模型参数辨识的思路进行整理：首先推导了2套INS输出角增量差值的自相关函数形式，即式（18）。其中，在简化角增量差值ΔΘk的过程中，设定了对 -δΘ1k×Φ项进行在线补偿。接着，通过对比式（18）和式（21），得出可以利用角增量差值的自相关函数对动态变形模型的参数进行辨识。选用粒子群算法，利用指数衰减正弦信号通式形式辅助建立算法模型，并合理设置了PSO参数以完成求参工作。

依照上述思路，动态变形模型参数的在线辨识流程设置如下，如图3所示。

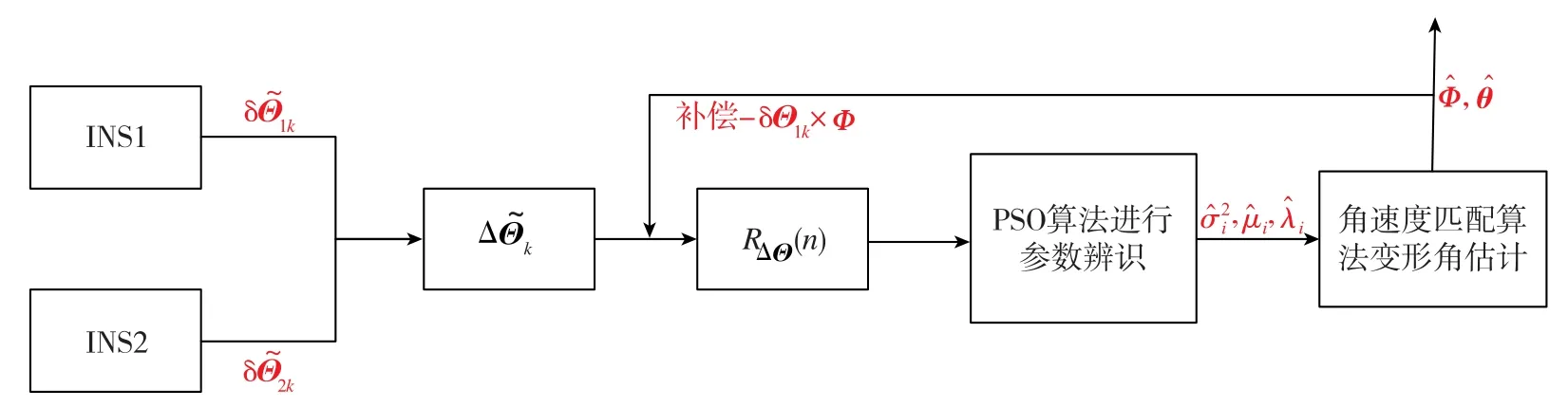
图3 基于PSO算法的动态变形模型参数在线辨识流程Fig.3 Online estimation procedure of dynamic flexure model parameters based on PSO

1）求2套INS在每个采样周期内的角增量输出差值ΔΘk，并补偿 -δΘ1k×Φ项。其中，第1次静态变形角Φ可由粗对准大致给出，之后由变形算法估计结果给出；

2）求解 ΔΘk自相关函数值 RΔΘ（n）；

3）将 RΔΘ（n）代入粒子群算法，利用式（28）进行参数辨识；

4）将辨识得到的参数应用于角速度匹配算法中进行变形角估计，将所估静态变形角Φ代回至步骤1，进行下一步解算。

对于PSO算法的参数设置，通过尝试和经验，将种群规模s设置为120；学习因子c1设为1.3，c2设为1.7；为保证收敛速度，同时避免陷入局部最优，将最大进化代数设为500；使用时变权重w（t），以确保PSO算法在全程中都拥有良好的搜索性能。

3 仿真实验

3.1 仿真条件

设置载体以5m/s的速度做定速直航行驶，其在3个方向的角运行模型如下

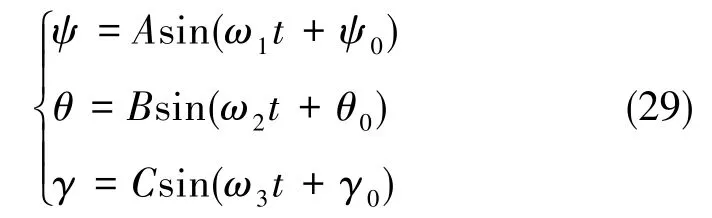
式（29）中，幅值 A＝5°、B＝4°、C＝4°，角频率ω1＝2π/7、ω2＝2π/6、ω3＝2π/8，初始相位 ψ0＝θ0＝γ0＝0。

表1 动态挠曲变形模型参数设置Table 1 Parameter setting of dynamic flexure deformation model

在仿真实验中，其他参数设置如下。

图4 动态挠曲变形角曲线Fig.4 Diagram of dynamic deformation angle curve

采样频率设为100Hz，采样时间为10min。

3.2 仿真结果

1）考虑无噪声情况，即动态挠曲变形信号的SNR→∞。选用20s的仿真数据进行角增量差值自相关函数RΔΘ（n）的计算，结果如图5所示。显然，2套INS在俯仰、横滚、航向3个方向的RΔΘ（n）均为指数衰减正弦信号形式。截取前15s的结果，代入PSO算法进行参数辨识。对50次独立实验的结果求取均值，结果如表2所示。

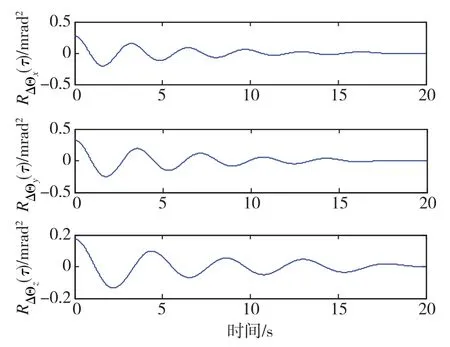
图5 无噪声条件下2套INS在3个轴向上角增量差值的自相关函数曲线Fig.5 Autocorrelation function curve of angular increment output difference in three axes without noise

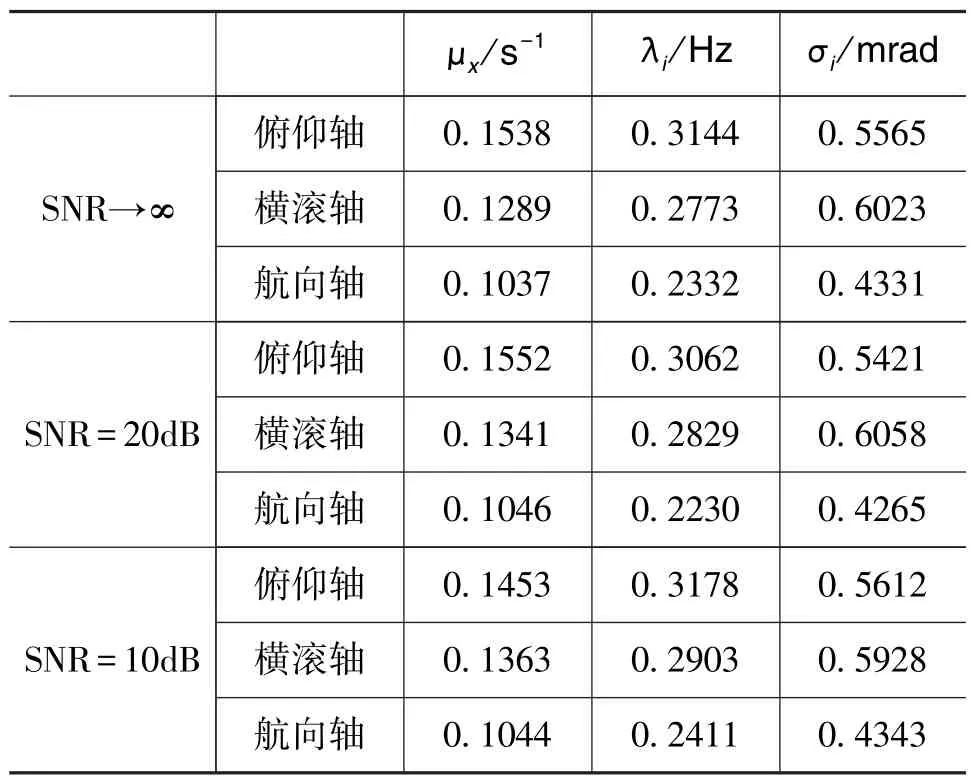
表2 不同信噪比情况下50次独立求参的结果均值Table 2 Mean value of the result of 50 independent parameter estimation experiments under different SNR conditions

2）在实际情况下，受舰船发动机振动等因素的影响，动态变形信号会带有高频噪声。首先考虑动态挠曲变形信号的SNR＝20dB的情况，人为地给动态挠曲信号加入噪声，并设置信噪比为20dB，考察在受噪声干扰情况下PSO算法的参数辨识能力。将角增量差值自相关函数曲线截取前15s结果，同样利用PSO算法进行50次独立求参实验并取均值，得到的结果如表2所示。

3）考虑动态挠曲变形信号的SNR＝10dB的情况。设置信噪比为10dB，进一步考察在高噪声干扰下的求参效果，最终结果由表2给出。

将辨识结果与真实参数进行比对，不难看出在不同程度的噪声干扰的情况下，利用PSO算法所辨识出的动态变形模型参数均具有较高的精度。将3组参数均应用于角速度匹配Kalman滤波器中进行变形角估计，得到的估计精度相当，这里给出了在SNR＝10dB条件下得到的参数测量结果，如图6所示。

结合PSO辨识算法之后的船体变形角估计结果与真实值十分接近，且由图6（c）可以清楚地看到，动态变形角估计曲线能够很好地跟随真实值的变化情况。图7给出了总变形角的估计误差曲线，对3个轴向的变形角估计误差求均方根（RMS），得到的结果为：10.11″、9.74″、10.25″。

图6 船体变形角估计结果Fig.6 Result of ship hull deformation angle estimation

图7 总变形角估计误差曲线Fig.7 Estimation error curves of total deformation angle

3.3 结果分析

仿真结果证实，本文提出的基于PSO算法的辨识方法能够有效辨识出船体动态变形模型参数，并且在不同程度的噪声干扰下均具有较高的辨识精度。

从结合该参数辨识算法的船体变形角估计结果来看，静态变形与动态变形曲线在3s以内即可收敛，且动态变形角曲线能够很好地跟随实际值，总变形角估计误差能够保证在10″左右，可满足工程应用的需要。

4 结论

本文通过将2套INS的输出角增量进行匹配，提出可以利用角增量差值进行船体动态变形模型参数的在线辨识。结合前人工作，推导了角增量差值自相关函数的具体形式，并借助指数衰减正弦信号通式建立了辨识算法模型。选择PSO算法作为辨识工具，合理设计了算法流程，设置了相应参数，最终细化为1套完整的基于角速度匹配并结合动态变形模型参数在线辨识算法的船体变形测量流程。通过仿真结果，得到如下结论：

1）本文提出的基于PSO算法的动态变形模型参数辨识方案，在不同信噪比条件下均具有良好的辨识性能；

2）结合该在线辨识方法的船体变形测量算法，所估静态变形角与动态变形角均能够很好地跟随真实值的变化，证明了参数辨识的可靠性；

3）最终的总变形角估计误差在10″左右，且算法简单有效，具备较高的工程应用价值。