一种基于语言D数的信息不完备多属性群决策方法

莫泓铭

（四川民族学院图书馆，四川康定626001）

决策是当前的研究热点之一，决策遍布于日常生活的每一个角落，如投资分析[1]、情感分析[2]、绩效评估[3]、台风预测[4]等.为提高决策结果的准确性，决策的参与者通常而言都是多人，即群决策. 在群决策中，准确而定量的信息是理想状态，然而现实中信息更多的是定性，甚至模糊的，这是由人类思维的犹豫性、不确定性及待决策问题的复杂性等主客观因素决定的. 决策者出于本能，习惯于运用自然语言给出对待评价对象的评价信息. 例如，在对政务中心某工作人员的服务态度进行评价时，常常采用诸如“很好”“不错”“还好”“一般”“很差”等语言信息进行描述. 相对于精确的定量信息，语言信息更易于决策者的本身感观信息表达，而不用纠结于精准而具体的数据值.

近年来，基于语言信息的决策方法得到了广泛研究，并取得了一定的成果，其研究方法大致可以分为三类. 第一类为扩展原理分析法[5-6]，其核心在于将语言评价信息转化为模糊数，基于扩展原理对模糊数进行运算与分析. 第二类为符号转移分析法[7-8]，其根据语言评价集自身的顺序与性质对语言术语符号等直接进行运算.第三类为二元语义分析法[9-10]，通过将决策者的语言偏好评价信息转化为二元语义符号，并根据二元语义的集成算子进行语义计算.

上述三种研究方法都是基于完备信息的这一前提，即决策者给出的评价信息是完整的、闭合的.然而，语言信息常常具有不精确和模糊等特性，在实际的决策过程中由于决策者自身的一些局限，例如对待评价对象相关属性的认识不充分、理解不透彻、自身知识水平缺乏、评估过程受到干扰等主客观原因，决策者无法对某一对象给出准确的评价，进而评价失败甚至导致出现不评价（弃权），即评价结果出现空值现象. 针对这一问题，目前主要有如下两种解决方案. 一是将不完全的信息进行补全，通常应用粗糙集理论[11]、数理统计[12]等方法进行数据补全.数据补全是在现有的数据的基础上，探寻数据规律，进而判断缺失数据的近似值.数据补全需要满足数据样本量大和数据可预测等两个特性.这种处理方法具有很强的主观性，进而有可能导致不如意的结果出现，并且在空值过多的情况下，如果现有数据样本较少，数据补全法是不可行的. 另一种方法是运用证据理论[13-14]的近似推理方法对不完全信息进行处理[15]. 证据理论可以表达“完全不知道”“不确定”等信息. 证据理论将这些空缺的数值视为“完全不知道”，即将该缺失的信息全赋给全集. 然而，研究发现，该方法存在结果不稳定，进而导致评价结果排序不唯一的情况[16]. D 数是一种新的不确定信息表达与处理工具，其基于证据理论的框架，是证据理论的有效扩展，但具有比证据理论更为灵活和更为宽松的应用条件.在D数理论中，信息缺失是允许，即其能明确的表达不知道与不确定这两种信息，而在证据理论中，这两种不同的信息是同一种的信息，同时不允许信息缺失.

基于此，针对决策问题中存在的信息不完全情况，本文提出一种新的基于D 数的语言评价多属性群决策方法. 在新提出的方法中，将决策者的语言评价信息（含完全与不完全信息）直接转化为D 数，根据D数的聚集属性对决策者给出的语言评价信息进行合成，并据此对决策方案排序，最终识别出合理的决策方案.

1 预备知识

1.1 证据理论基础

证据理论（Dempster-Shafer evidence theory）是Dempster 于1967 年提出的一种用于处理不确定信息的数学工具[13]，随后其学生Shafer 于1976 年进一步推广和完善而来的[14]. 证据理论相对于传统的贝叶斯概率论而言，不需要任何先验信息，并且将贝叶斯概率论中的单子集赋值推广到单子集的幂集空间赋值，应用范围更广. 此外，证据理论除了表达“不确定”信息，还可以表达“完全不知道”等信息.由于其强大的信息表达与信息融合能力，证据理论被广泛应用于模式识别、故障诊断、风险评估及决策分析等领域[17-21].证据理论的定义如下：

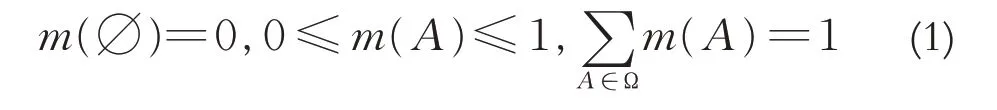
其中∅是空集，A是集合Ω的任意子集.

Dempster 组合规则是证据理论的核心，或称为两个BPA的正交和，其实现不同证据源的融合并得到新的证据.Dempster组合规则定义如下：

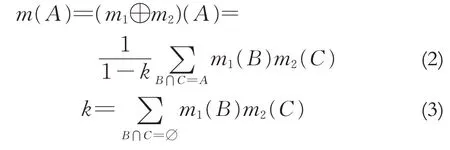
其中，k 是冲突系数，反映的是两个BPA 的相容程度. 当k=0 时，意味着两个BPA 是完全一样的；当k=1 时，代表两个BPA 是完全冲突的，即彼此互相矛盾，此时，Dempster 组合规则是无效的. Dempster组合规则满足交换律和结合律，即①m1⊕m2=m2⊕m1，②(m1⊕m2)⊕m3=m1⊕(m2⊕m3). 因此，当存在多个BPA需要融合时，可以不用考虑其先后顺序而一对一对地对其进行融合.

1.2 D数基础

证据理论相对于传统的贝叶斯概率论而言，在信息的表达与融合等方面得到了一定的突破，应用范围也更广，然而证据理论在具体应用时，也存在许多限制条件. 其一，辨识框架中的任意两元素必须完全独立，即两两互斥. 显然，在诸如“很好”“好”“一般”“将就”等语言评价元素中，它们不是完全独立互斥的，即这些信息之间难免存在一定的交叉.其二，BPA 的概率分配之和必须为1，即必须满足完整性这一约束条件. 然而在现实中，专家由于知识经验不足，或者缺乏足够的把握等主客观原因，进而得到一个不完整的BPA是合理的，即BPA概率值之和小于1.其三，证据理论组合规则的运算时间复杂度高，当证据源呈线性增长时，其组合规则算法的时间复杂度呈指数级增长，这也限制了证据理论的进一步应用.其四，在运用证据理论的组合规则时，要求各证据源之间必须彼此两两独立，毫无关联，这在实际应用中有时无法达成，例如某专家在评估时，可能受到别的专家的评估信息干扰，也有可能受到待评估对象相关信息的干扰.

为解决证据理论在应用中的这些限制，邓勇于2012 年提出了一种新的不确定信息表达与处理工具——D 数理论[22]. D 数理论是证据理论的有效扩展.在D数理论中，元素之间不强行要求互斥；同一D 数内的各元素信任度之和允许小于等于1，即允许根据实际情况灵活表达评价信息.此外，D数的聚集属性完美地解决了证据理论组合规则的指数级运算时间复杂度问题. 由于D 数在处理不确定、不完备信息等方面的优势，D 数理论目前被应用于桥梁评估[23]、环境评估[24]、供应商选择[25]、安全评估[26]等领域，并取得了很好的效果. D 数理论的相关定义如下：

假设Ω为非空有限集合，D数是一个映射，即D：Ω →[0,1]，满足以下条件：

其中∅是空集，A 是集合Ω 的任意子集. 值得一提的是，集合Ω 中的元素不要求互斥并且识别框架可以不完备，即所有同一D 数的映射和可以小于等于1，而不必硬性要求等于1，这是与证据理论最大的不同之一.当∑A⊆ΩD(A)=1时，该信息被称为是完备的，否则是不完备的. 基于此，D数可以很灵活地表达不确定信息，专家们可以根据自身的知识、经验等实际情况合理地表达自己的观点，而不用考虑其观点是否完备的问题.

假如Ω={d1,d2,…di…dn}，一种特殊形式的D数 可 以 表 示 为D(d1)=v1, …D(di)=vi，… ，D(dn)=vn，可简化为

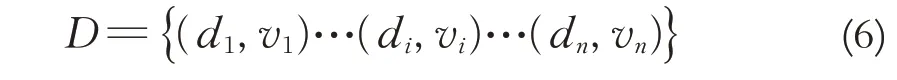
与证据理论类似，D数也具有相应的属性.

属性1：交换不变性.假设在同一框架上有2个D 数D1={ }(d1,v1)…(di,vi)…(dn,vn) 和D2={}(dn,vn)…(di,vi)…(d1,v1) ，那么D1和D2被认为是完全相同的.

例1：假设有2 个D 数D1={(A,0.4),(B,0.4),(C,0.2)}和D2={(B,0.4),(C,0.2),(A,0.4)}，则D1和D2是完全相同的.在本例中，D1和D2的信任度之和均为1，说明这2个D数是完备的.

例2：假设2 个D 数D1={(good,0.8),(bad,0.1)}和D2={(bad,0.1),(good,0.8)}，则D1和D2是完全相同的.在本例中，D1和D2的信任度之和均为0.9，小于1，说明这两个D数都是不完备的.需要说明的是，这种情况在证据理论中是不允许存在的.

例3：假设在证据理论的同一辨识框架上有2组BPA 即E1={(a,0.5),(b,0.3),(c,0.2)} 和E2={(b,0.3),(a,0.5),(c,0.2)}，那么E1和E2是 完全相同的.

从上述3 个例子可以看出，在信息完备的情况下，D 数的交换不变性在证据理论中也是同样适用的.

属性2：聚集性.假设存在一个特殊的离散型D 数D={ }(d1,v1)…(di,vi)…(dn,vn) ，那么D 数的聚集操作可以表示为

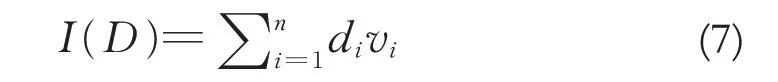
其中di∈R+，vi＞0，vi的和小于等于1.

例4：假设一个D 数D={(1,0.2),(3,0.4),(5,0.2),(7,0.2)}，那么

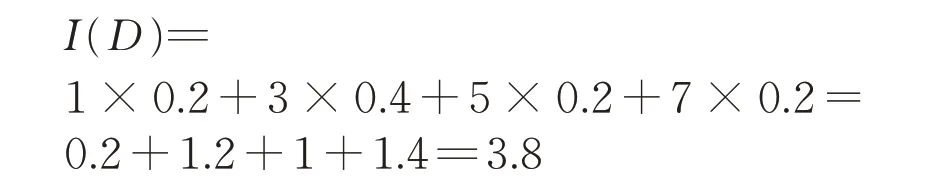
例5：假设一个D 数D={(2,0.3),(3,0.1)}，那么I(D)=2×0.3+3×0.1=0.9.

需要说明的是，聚集属性仅适用于特殊的离散型D 数. 在决策评估中，合理利用D 数的聚集属性将大大简化和加快决策评估过程.

2 决策模型与方法

2.1 问题描述

在一个多属性群决策问题中，假设有n 个决策方案（或候选者），其方案集为C={Ci,i=1,2,…,n}；每个方案由m 个属性组成，即方案的属性集为A={Aj,j=1,2,…,m}；不失一般性，为每个属性分配相应的权重，即有属性权重集W={Wj,j=1,2,…,m}，其 中Wj=1；有 p（p ≥2）位专家（或决策者）参与决策，决策者集为E={Ek,k=1,2,…,p}. 为决策者提供预先定义好的由奇数个语言构成的评价语言集，通常而言语言评价集中的元素为奇数个，数量太多或太少均不太适合，数量可为3 个、5 个、7 个及9 个，通常以7 个为佳，即有语言评价集L={L0,L1,L2,L3,L4,L5,L6}. 决策者Ek采用语言评价集中的元素对方案Ci的属性Aj下的评值可由函数fk(Ci,Aj)来表示，即得到决策者Ek的评价矩阵为EVk=[ fk(Ci,Aj)]n×m.在决策方案的属性指标中，有的属性指标是效益型的，即数值越大越好，有的属性指标是成本型的，即数值越小越好.因而在本文中，对应的语言评价集L(收益型/成本型)={L0,L1,L2,L3,L4,L5,L6} =｛最低/最高、很低/很高、低/高、一般/一般、高/低、很高/很低、最高/最低｝. 当决策者不愿意或者不能给出方案Ci在属性Aj下的语言评价信息时，用“～”表示，表示无语言评价信息，即在语言评价矩阵中有fk(Ci,Aj)=～.

2.2 决策过程

在解决多属性群决策问题时，关于数据的处理，常用的有两种解决方案[27-28]. 一是在统一的标准下先合成各决策者对待评价方案属性给出的评价，即将多属性群决策问题视为多属性的个体决策问题，然后再选用相关的决策方法来进行求解.该方法要求决策者都采用相同的决策属性，同时各决策者对属性的权重分配也应是相同的，这种方法适用于决策者众多的场景，有利于数据的快速整合，但决策者的个性化评价及指标等因素无法体现.二是决策者先自行评估再分别集成融合.即允许决策者根据自己的意愿，分别对各属性的权重进行个性化设定，并对各属性进行评价，待评价完成后，采用相关的决策融合方法对不同的决策者的评价结果进行综合，进而得到各待评价方案的评价综合值.在上述两种方法中，决策者在实施评价之前，都需要组织者先提供候选方案、方案的属性及语言评价集等公共参数.在本模型中，为让决策者从自身情况出发，更好地做出符合实际的评价，因而采用第二种方案，决策过程如图1所示.

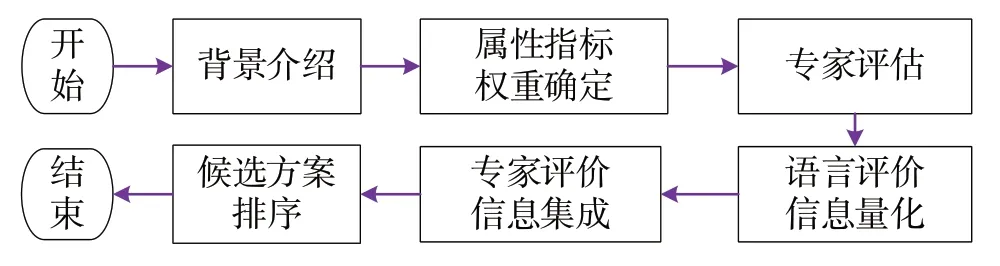
图1 决策评估流程Fig.1 The processes of decision making

具体步骤如下：

第一步，背景介绍. 向专家介绍决策问题的基本情况，重点是向专家介绍即将要进行的评价决策情况，含候选者及其属性、评价所采用的公用语言评价集等.

第二步，属性指标权重确定. 专家在对候选方案及其属性有充分了解的基础上为各属性指定相应的权重.

第三步，专家评估. 专家根据获得的相关信息并结合自身情况，对各候选方案进行评估.

第四步，语言评价信息量化. 提供统一的语言评价信息量化对照表，并对语言量化信息进行归一化处理.

第五步，专家评价信息集成. 运用D 数工具对分别对各专家的评价信息进行集成，得到各专家对各候选方案的总体评价.

第六步，候选方案排序. 集成专家对各候选方案的评价结果，进而得到各候选方案的最终评价得分，并据此排序，找出最佳候选者.

3 案例应用

某汽车制造公司拟选择一家物流服务商将其汽车运往全国各地经销商处，经初步调查有A、B、C、D等四家物流服务商进入候选.为选择更好的物流服务商，该公司拟邀请3位业内专家（决策者）E1、E2、E3对A、B、C、D等4家物流服务商进行综合测评.

第一步，结合该公司业务需求及对物流服务商的要求，确定了以下4个主要考核属性：操作可靠性（Operational Reliability,OR）、物流成本（Logistics Cost,LC）、服务水平（Service Level,SL）和管理水平（Management Level,ML）.提供语言评价集L供专家在评估时采用.

第二步，各专家在对物流服务商的4 个主要考核属性进行充分理解的情况下，结合自身情况，给出了4 个属性的权重向量Wkj（其中k=E1,E2,E3;j=OR,LC,SL,ML），分别为：

第三步，3位专家对各物流服务商进行评估，评估结果分别如表1至表3所示（表中“～”代表空值，即专家出于某些原因没有给出任何评价信息）.

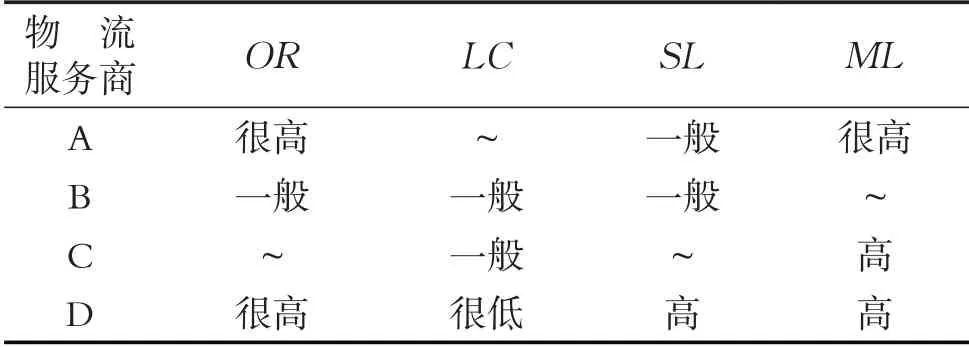
表1 专家E1提供的物流服务商评价信息Table 1 The evaluation results of logistics service providers by expert E1

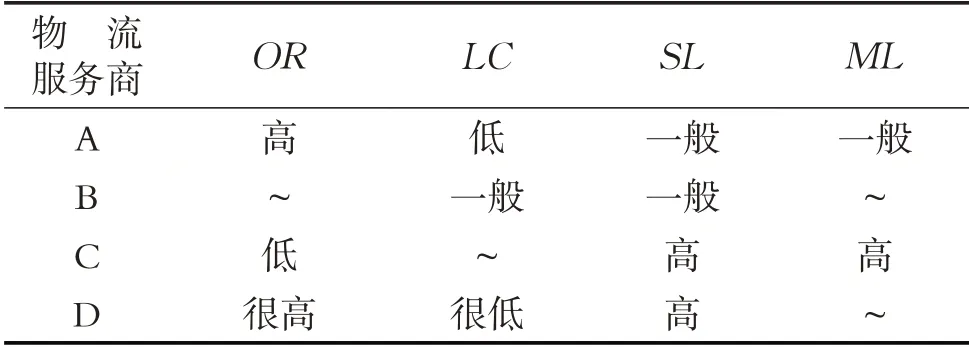
表2 专家E2提供的物流服务商评价信息Table 2 The evaluation results of logistics service providers by expert E2

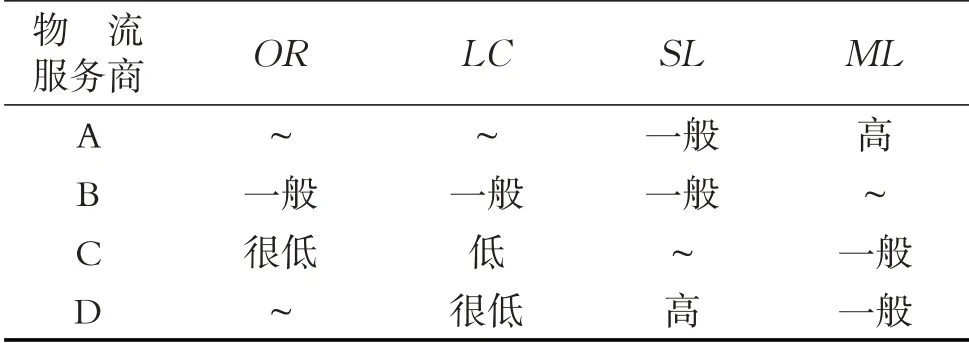
表3 专家E3提供的物流服务商评价信息Table 3 The evaluation results of logistics service providers by expert E3

第四步，为将专家的评估信息量化，需先将语言评价信息量化处理. 在本例中，采用两级比例法对其进行转化[27]，并对其进行归一化处理，如表4 所示.需要说明的是，对于收益类属性，其值是越大越好，而对于成本类属性，其值则是越小越好.为统一数值标准，表4 基于成本类属性与收益类属性提供了相同的属性量化值，但成本类属性与收益类属性其对应的评价标准却是相反的. 在决策过程中，当两种类型的属性皆存在时，需加以留意.

表4 语言评价信息等级量化表Table 4 Reference of linguistic assessment information

以专家E1为例，由表1可知，其对4家物流服务商的评价的语言D数表示为：

结合专家E1 对各属性的权重分配，如公式（8）所示，公式（11）可转化为：

将公式（8）和表4中的相关数值代入，公式（12）可进一步转化为：

公式（13）体现了专家E1 对物流服务商A 的各属性评估情况，公式（14）体现了专家E1对物流服务商B的各属性评估情况，公式（15）体现了专家E1对物流服务商C 的各属性评估情况，公式（16）体现了专家E1对物流服务商D的各属性评估情况.

运用D 数的聚集性属性，如公式（7）所示，将公式（13）至公式（16）分别集成，即得到专家E1对物流服务商A、B、C、D的最终评价为：

其中，IE1(A)代表专家E1对物流服务商A的最终评估值，IE1(B)代表专家E1对物流服务商B的最终评估值，IE1(C)代表专家E1对物流服务商C的最终评估值，IE1(D)代表专家E1对物流服务商D的最终评估值.

同理，可得专家E2和E3分别对物流服务商A、B、C、D的最终评估值，如表5第3、4列所示.

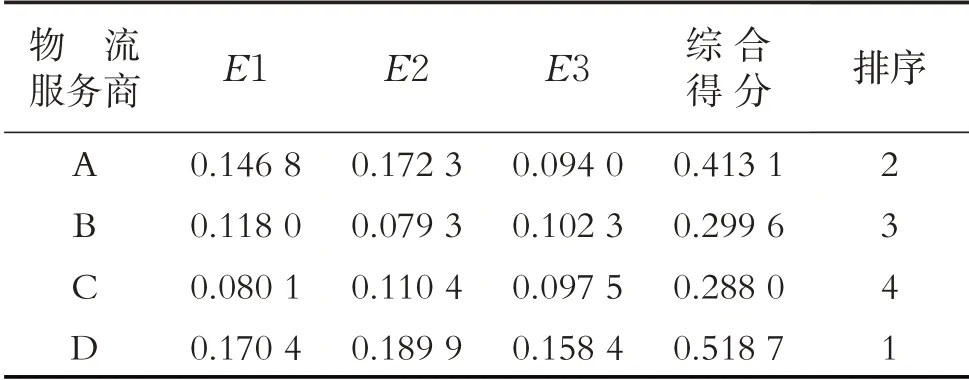
表5 专家对各物流服务商最终评估值Table 5 The final evaluation result of logistics service providers by experts

第六步，通过对各专家的评估结果进行汇总，即可得到各物流服务商的评估综合值及据此排序，如表5第5、6列所示.可知，物流服务商的候选顺序为D＞A＞B＞C.

本文所提出的决策模型识别结果与文献[15]和[16]结果一致，均为D＞A＞B＞C. 然而，文献[15]和[16]所识别的结果均为区间数表现形式，而本文的识别结果为精确数形式，定量表达，更为直观并易于比较.

需要说明的是，在本例中，仅考虑了各属性指标的权重，而没有考虑各评估专家的权重，或者说，各专家的权重被视为一样的. 在实际应用中，由于知识、经验或其他主客观因素等的倾向与限制，各专家对问题的判定是存在差异的，因而为参与评估的专家分配不同的权重是合理的，专家及各属性指标权重对决策结果也是有影响的.

4 结语

本文提出了一种基于语言D数的不完全信息多属性决策方法，允许决策专家对候选者进行合理的评价，而不用考虑评价数据的完整性约束，专家在评估时具有灵活性. 待收集到专家的评价信息后，将专家的评价信息视为D 数，进而运用D 数的相关特性进行信息分步集成，最终得到候选者的最终评估得分，进而依此进行排序.案例分析表明，该决策模型具有科学性与有效性，且流程直观明了、清晰，时间复杂度低. 在下一步的工作中，将进一步拓展权重分配体系，使其更加结合实际情况.