基于支持向量回归的关中平原冬小麦估产研究

曾 妍，王 迪※，赵小娟

（1. 中国农业科学院农业资源与农业区划研究所/农业农村部农业遥感重点实验室，北京100081； 2. 青海省农牧业遥感中心，西宁810008）

0 引言

小麦在中国是仅次于水稻、玉米的第三大粮食作物［1］，小麦估产可为有关部门制定政策和经济计划提供依据，在粮食生产、流通和储备等各环节的宏观调控中发挥作用。中国是全球最大的小麦生产国和消费国，常年产量约占全球17%［2］，中国小麦产量变化对全球小麦产量的预测有重要影响，进而波及到国际粮价的稳定，因此，及时准确估测中国的小麦产量对保证全球粮食安全具有重要意义。

卫星遥感能及时高效地获取大范围地物信息，广泛应用于农业监测领域，其中产量估算更是农情遥感监测的重要内容。目前，基于遥感信息的作物产量估测方法主要有3种：经验模型或统计模型、机理模型和半经验半机理模型［3-4］。机理模型能够反映作物产量形成过程，但输入参数多且校正困难，导致其应用受限。相较于机理模型，半经验半机理模型虽有简化，但模型输入中需要的2个关键变量，光能利用效率和作物收获指数，都难以在时空分布中进行准确地定量模拟［5］。统计模型方法尽管对作物产量形成的机理解释性不强，但其结构简单、可操作性强，契合作物估产的业务化应用需求，因此仍然是当前作物遥感估产的常用方法。

经验模型以数学统计分析方法为基础，包括线性模型和非线性模型。而粮食产量受众多不确定因素的影响，是一个复杂的非线性系统，所以非线性估产模型的精度通常高于线性模型［6］。支持向量回归（Support Vector Regression，SVR）方法是近年来广泛应用的一种非线性回归模型，其基本思想是，找到一个回归平面，让一个集合内所有数据到该平面的距离最近［7］。相较于神经网络等机器学习方法，它的拟合和泛化推广能力更优异［8-9］，在解决粮食估产等非线性、小样本的实际问题上具有较大 优势。

构建估产模型多采用与粮食产量具有高度相关性的参数，包括植被指数、太阳光合有效辐射、生物量等［10］，其中应用最广泛的是能够反映植被绿度状态的归一化植被指数（Normalized Difference Vegetation Index，NDVI）［11-13］。然而，除植被绿度状态以外，影响农作物生长的土壤水分、气温等指标也与产量的形成紧密关联。为此，文章综合考虑作物生长过程中的水分胁迫指标、作物生长状态指标，选取条件植被温度指数（Vegetation Temperature Condition Index，VTCI）、叶面积指数（Leaf Area Index，LAI）作为模型输入变量，采用支持向量回归方法建立遥感估产模型，并对该方法的精度进行评价，为及时、准确的区域小麦估产提供新的解决途径。

1 材料与方法

1.1 研究思路

回归的基本思路是利用有限的样本数据，建立输入和输出之间隐含的函数关系。该文在MATLAB环境下，通过LIBSVM3.23工具包［14］，采用支持向量回归方法，基于所选的核函数和最优参数构建产量估测模型，找到各影响因素对产量最佳的映射关系，利用实际产量数据对模型模拟结果进行精度评价，技术路线如图1所示。

1.2 研究区概况

研究区为陕西省中部关中平原（图2a）的5个市，西安市、宝鸡市、咸阳市、渭南市、铜川市，地处106°18′E～110°35′E，33°35′N～35°52′N（图2b），总面积5.53万km2。 关中平原三面环山，渭河横跨平原，地势西高东低，中部较为平坦宽阔，平均海拔约400 m。地属大陆性季风气候，多年平均气温13.9℃，多年平均降水量595.3 mm。该区域气候温润、水系纵横、土质疏松，是我国重要的粮食产区，也是重要的麦、棉产区，小麦占其耕地面积的50%左右。当地耕作制度为两年三熟，作物种植模式主要是在灌溉区内进行冬小麦、夏玉米轮作，在旱作区域进行夏季休闲式的冬小麦 连作［15］。

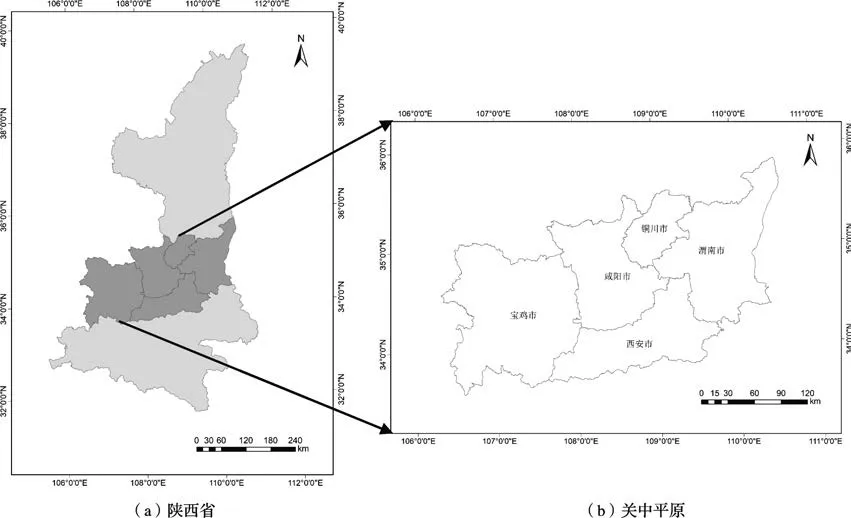
图2 研究区地理位置Fig.2 Location of study area

1.3 数据源

该文采用的遥感数据是研究区内2011—2016年冬小麦主要生育期（3月上旬至5月下旬）的Aqua-MODIS日地表反射率产品（MYD09GA）、日地表温度产品（MYD11A1）、叶面积指数产品（MCD15A3）。所用的产量数据来源于2011—2016年的《陕西省统计年鉴》。将各市的小麦种植面积以及总产量汇总，表1中列出了计算后得到的对应年份各市冬小麦单产数据。

表1 2011—2016年研究区5市冬小麦单产Table 1 Yield per hectare of winter wheat of research area in five cities from 2011 to 2016 kg/hm2

1.4 研究方法

1.4.1 VTCI计算

条件植被温度指数（VTCI）是基于归一化植被指数（NDVI）和地表温度（LST）特征空间呈三角形区域分布的特点提出的，能体现植物生长过程中受到的水分胁迫，是一种近实时的干旱监测方法，计算方法为［16］：

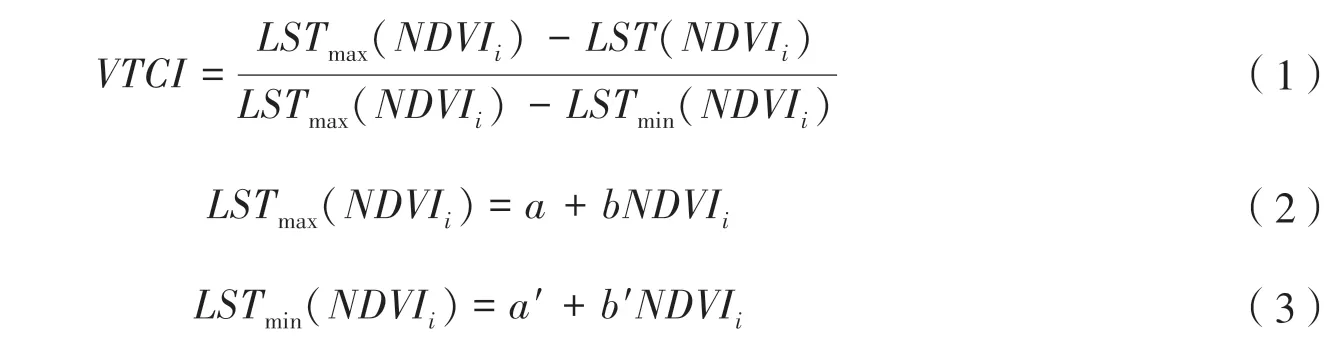
式（1）～（3）中，LSTmax（NDVIi）、LSTmin（NDVIi）分别被称作热、冷边界，表示在研究区内，当NDVIi值为某一特定值时，所有像素地表温度的最大值和最小值；LST（NDVIi）表示某一像素的NDVI值为NDVIi时的地表温度；a，b，a′，b′是待定系数，由研究区内的NDVI和LST散点图近似得到。

计算VTCI采用的遥感数据是研究区内2011—2016年冬小麦主要生育期（3月上旬至5月下旬）的Aqua-MODIS日地表反射率产品（MYD09GA）、日地表温度产品（MYD11A1）。利用MODIS重投影工具MRT（MODIS Reprojection Tools）对原始数据进行拼接、重采样、投影转换等预处理操作后，得到研究区日LST和日地表反射率数据。利用日地表反射率数据计算日NDVI，用最大值合成方法分别生成逐像素的旬LST和旬NDVI最大值合成数据，并按照VTCI定义计算出旬VTCI。

将冬小麦的主要生育期划分为4个生育时期，结合关中平原冬小麦越冬后的生长情况，将返青期定为3月上旬至3月中旬，拔节期为3月下旬至4月中旬，抽穗—灌浆期为4月下旬至5月上旬，乳熟期为5月中旬至5月下旬［17］。计算每个生育期内各旬VTCI的平均值作为该生育期的VTCI值，计算研究区2011—2016年5市各生育期的VTCI。

1.4.2 LAI计算

采用2011—2016年冬小麦主要生育期内的叶面积指数产品（MCD15A3）计算LAI，这一产品每4 d合成1次，时间分辨率较高，空间分辨率为500 m，有利于农作物长势监测。同样对影像进行投影转换、裁剪等预处理，利用S-G滤波器消除云和大气等噪声，改善数据质量。然后采用取最大值的方法逐像素地生成旬LAI，取各生育期内所包含的多旬LAI的均值分别作为该生育期LAI，实现LAI、VTCI时间分辨率的 统一。

1.4.3 SVR模型构建

①支持向量回归

支持向量回归的基本思想是采用一个非线性映射把数据映射到高维特征空间，然后在高维特征空间构造回归估计函数，再映回到原空间。通过定义适当的核函数k（x，xi）来实现非线性变换，无需得到确切的映射函数Φ（x），给计算带来了极大方便［18］。回归方程为：

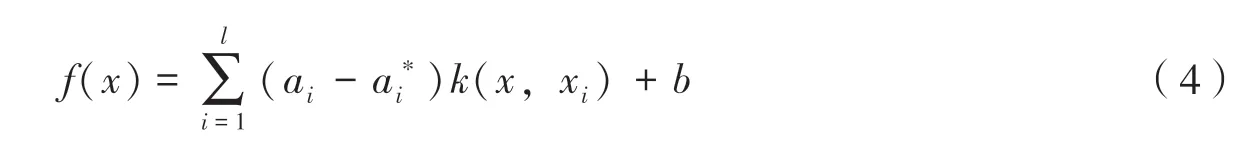
式（4）中，ai-a*

i是各支持向量的系数。

②格式转换及归一化

通过运行FormatDataLibsvm.xls，将数据格式转化为LIBSVM规定的输入格式。为避免数据之间的量级差别，对VTCI、LAI、单产数据分别采用归一化处理，归一化公式 为：

式（5）中，Xmax和Xmin分别为数据中的最大值和最小值，经过归一化消除了模型输入由于量纲和单位不同造成的影响，使样本数据更加适应回归建模与分析。

③核函数选择

支持向量回归包括线性和非线性，在线性回归的基础上引入核函数，得到非线性回归。支持向量回归将高维空间内积运算化简成了从低维空间进行输入的核函数计 算［19-20］，选择的核函数的类型决定了支持向量回归的很多特性，从某种程度上直接影响着回归模型的拟合能力和预测精度。因此，核函数的选择是用支持向量回归预测粮食产量的一个关键步骤。

常用的核函数有多项式核函数、径向基（RBF）核函数（即高斯核函数）、Sigmoid核函数等，选用不同的核函数可以构造出不同的支持向量回归模型。

许多实验研究表明［21-22］，当缺少先验知识时，选用径向基核函数训练建模的效果较好，所得模型的总体性能较高，而且径向基核函数只含一个未知参数σ，易于进行优化，所以该研究选择的核函数为径向基核函数。公式为：

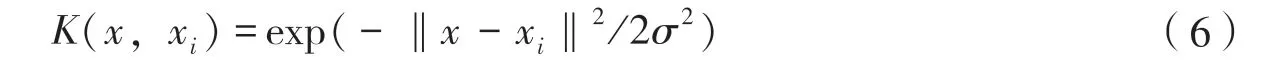
④参数寻优

在用支持向量回归解决实际问题时，参数的选择对回归模型的性能影响很大。应用RBF核函数时，惩罚因子C和参数σ与回归模型的学习性能息息相关。惩罚因子C用于控制模型对误差范围以外的样本的惩罚程度，也可以说是对离群点的重视程度，惩罚因子过高会造成过拟合。径向基核函数的参数σ反映了训练样本数据的范围或分布，确定局部邻域的宽度。

该研究选用LIBSVM中的ε-SVR方法，用网格搜索和n-fold交叉验证的方法进行参数寻优，确定C和σ值。当有不同的C和σ都对应最高的精度时，把参数C最小的那组C和σ作为最佳参数，避免惩罚参数C太高造成过学习状态。

1.4.4 模型精度评价

该文选取决定系数（Coefficient of Determination，R2）、均方根误差（Root Mean Square Error，RMSE）、平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）作为模型拟合程度的评价指标，具体公式为：

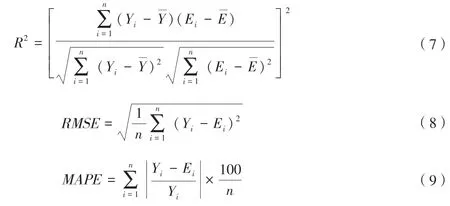
式（7）～（9）中，i表示第i个样本点数据，Yi为第i个实际产量，单位为kg/hm2；Ei为根据模型拟合的冬小麦产量估算值，单位为kg/hm2；为实际产量的均值，单位为kg/hm2；为模型估测产量的均值，单位为kg/hm2。

2 结果与分析

2.1 回归结果及误差分析

研究以2011—2015年研究区的数据作为训练集，采用SVR算法构建冬小麦估产模型，图3为2011—2015年研究区各市的实际产量和回归产量，可以看出预测产量和对应的实际产量波动的趋势大致相符。以实际产量和估测产量分别为横纵坐标绘制散点图（图4），添加趋势线和45°参考线，趋势线对比参考线偏离较小，可见模型对测试集的拟合效果较好。计算模型对训练集样本的预测精度，回归模型具有较高的决定系数R2=0.88，估测产量与实际产量间的RMSE为336.39 kg/hm2，MAPE为6.12%。

对训练集的拟合学习说明了SVR构建的模型能够以较小的误差拟合历史数据。采用构建好的模型预测2016年5市冬小麦单产，表2为预测结果及误差，可见5市数据共同构建的模型进行单产估测时有一定误差，其中面积较小的铜川市的相对误差较小，仅有1.28%。分别对2011—2015年5市冬小麦产量数据进行建模预测（表3），预测结果的RMSE平均值为232.63 kg/hm2，其中宝鸡市、渭南市的MAPE低至2.98%、3.37%，5市MAPE的平均值为5.74%，可见模型精度较高。

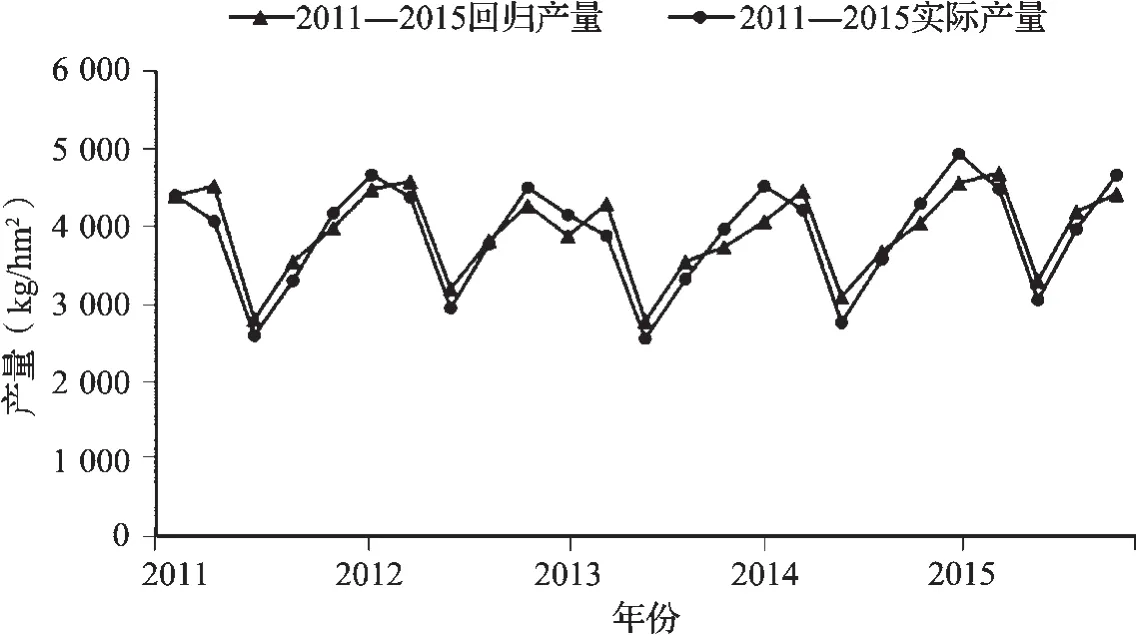
图3 2011—2015年5市冬小麦实际产量与回归产量对比Fig.3 Comparison of actual yield and regression yield from 2011 to 2015

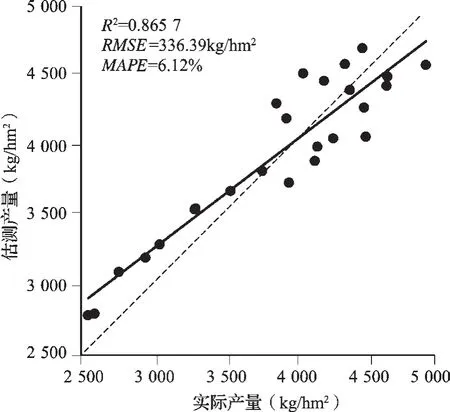
图4 训练集拟合情况Fig.4 Fitting effect of training set

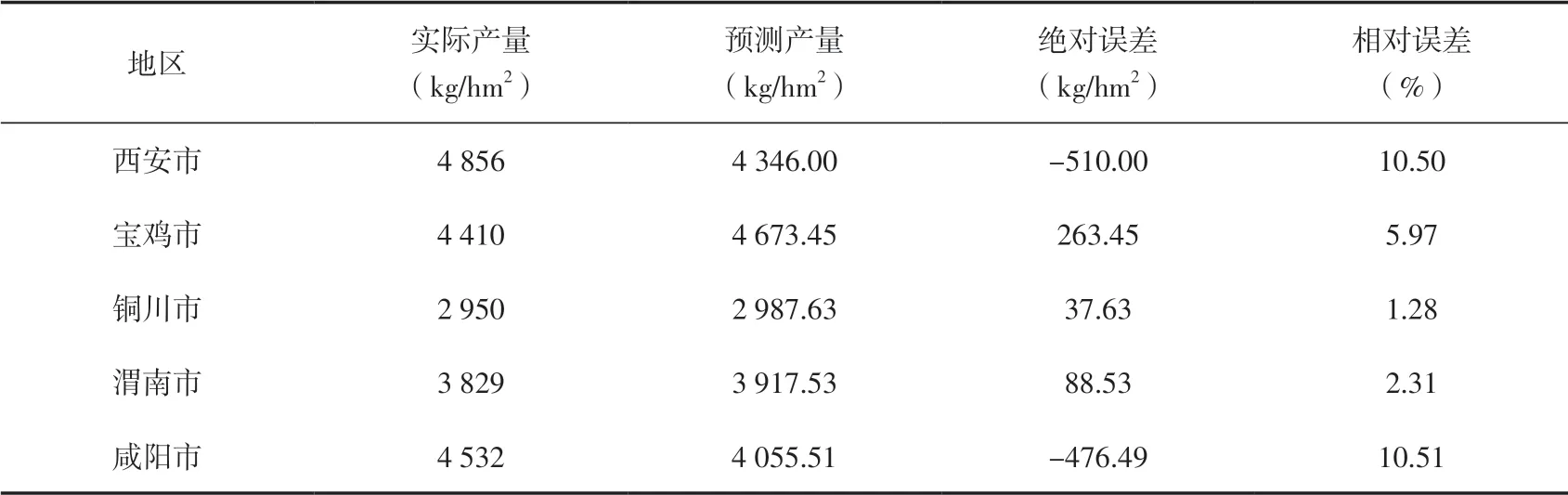
表2 2016年5市冬小麦回归预测结果及误差Table 2 Regression prediction results and errors

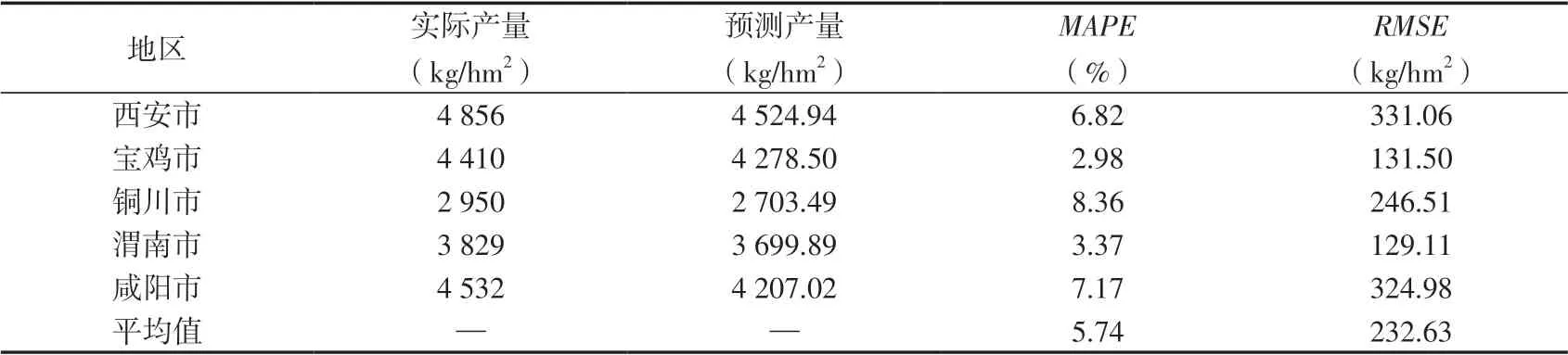
表3 5市分别构建回归模型的预测结果及精度Table 3 Prediction results and accuracy of regression models constructed by different municipalities

2.2 参数敏感性分析

通过观察不同参数对预测精度的影响，判断对预测精度提高帮助最大的参数。图5、图6给出了C和σ值变化时3个误差评价指标的相应变化。结果显示，发生同等程度的变化时，核参数σ引起的MAPE、RMSE、R2的改变都比惩罚因子C引起的改变更大。因此，核参数σ比惩罚因子C更重要。对2个参数进行耦合分析，发现该研究中当惩罚因子C为2、核参数σ为0.354时模型精度最高。

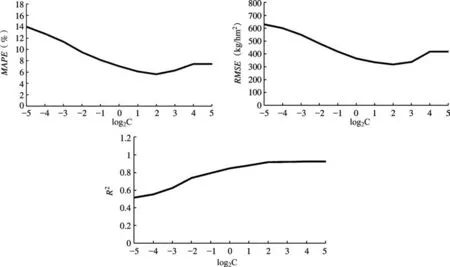
图5 不同参数C条件下的回归模型精度变化Fig.5 The accuracy change of regression model under different parameter C

3 结论与讨论

3.1 结论

该研究计算了2种与植被生长状况息息相关的参数——VTCI、LAI，将冬小麦各个生育期的VTCI和LAI作为输入变量，划分训练集和测试集，用支持向量回归算法对这些数据进行学习和训练，从而找到其内部隐含的函数关系。寻找最优的模型参数，建立冬小麦各生育期的VTCI、LAI与冬小麦产量之间的支持向量回归估产模型。

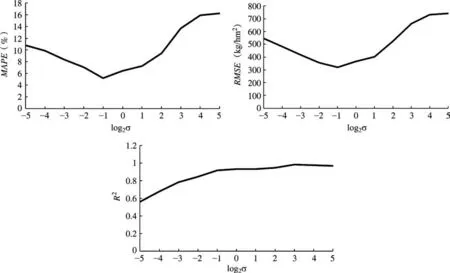
图6 不同参数σ条件下的回归模型精度变化Fig.6 The accuracy change of regression model under different parameter σ

支持向量回归模型较好地反映了输入的影响因素VTCI、LAI同冬小麦单产之间的复杂的非线性映射关系，建立的回归模型决定系数达到0.88，模型拟合较为理想，此外，模型参数的选取对模型精度有明显的影响，径向基核参数σ比惩罚因子C对预测结果影响更大。

该文采用支持向量机方法对关中平原的冬小麦产量进行预测，在样本较少的情况下，建立的回归模型精度较高，能够推广到其他地区，也可以为其他作物的产量预测研究提供参考，该方法在粮食产量预测领域有良好的应用前景。

3.2 讨论

该文仅选用了VTCI和LAI 2个指标，只能在一定程度上描述作物本身的生长状态。实际上，影响粮食产量的外部因素众多，还包括很多非遥感信息，如自然灾害、劳动主体的积极性、农业科技水平、农业的基础设施等。该研究缺少足够的先验知识，模型设置过于理想化，并未充分考虑多层次的因素，若要得到更为科学合理的估产结果，仍需继续探索与粮食产量密切相关的指标。

该研究核函数的选定依照前人的经验，而无充分的理论支撑，因此核函数的选用是未来需要进一步研究的内容。随着新技术的不断涌现，支持向量回归和其他理论方法的结合值得深入发掘，例如参数寻优可采用粒子群优化算法［23］、遗传算法，核函数可选用混合核函数［24］等。

此外，该研究采用统计年鉴的产量数据进行验证，但产量数据不可避免地存在着差错或漏报［25］, 因此如何有效验证模型精度也是有待解决的问题之一。